1.1.1 空间向量及其运算 同步练习(含解析)
文档属性
| 名称 | 1.1.1 空间向量及其运算 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 185.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 15:56:33 | ||
图片预览


文档简介
第一章 空间向量与立体几何
1.1 空间向量及其运算
1.1.1 空间向量及其运算
基础过关练
题组一 空间向量的概念
1.如图,在长方体ABCD-A'B'C'D'中,下列说法正确的是 ( )
A.=
B.||=||
C.向量与共线
D.向量与共面
2.(2022重庆开州中学月考)下列说法正确的是( )
A.若两个空间向量相等,则表示它们的有向线段的起点相同,终点也相同
B.若向量,满足||>||,且与同向,则>
C.空间四边形ABCD中,,为相反向量
D.同一条直线上的单位向量不一定相等
3.(2023北京首师大附属密云中学段考)下列说法正确的是 ( )
A.将空间中所有的单位向量的起点平移到同一个点,则它们的终点构成一个圆
B.若空间向量a,b满足|a|=|b|,则a=b
C.若空间向量m,n,p满足m=n,n=p,则m=p
D.若a与b共线,b与c共线,则a与c共线
题组二 空间向量的线性运算
4.(2022山东济宁邹城二中月考)在正方体ABCD-A1B1C1D1中,下列各式的运算结果为向量的是 ( )
①--;
②+-;
③-+;
④-+.
A.①② B.②③
C.③④ D.①④
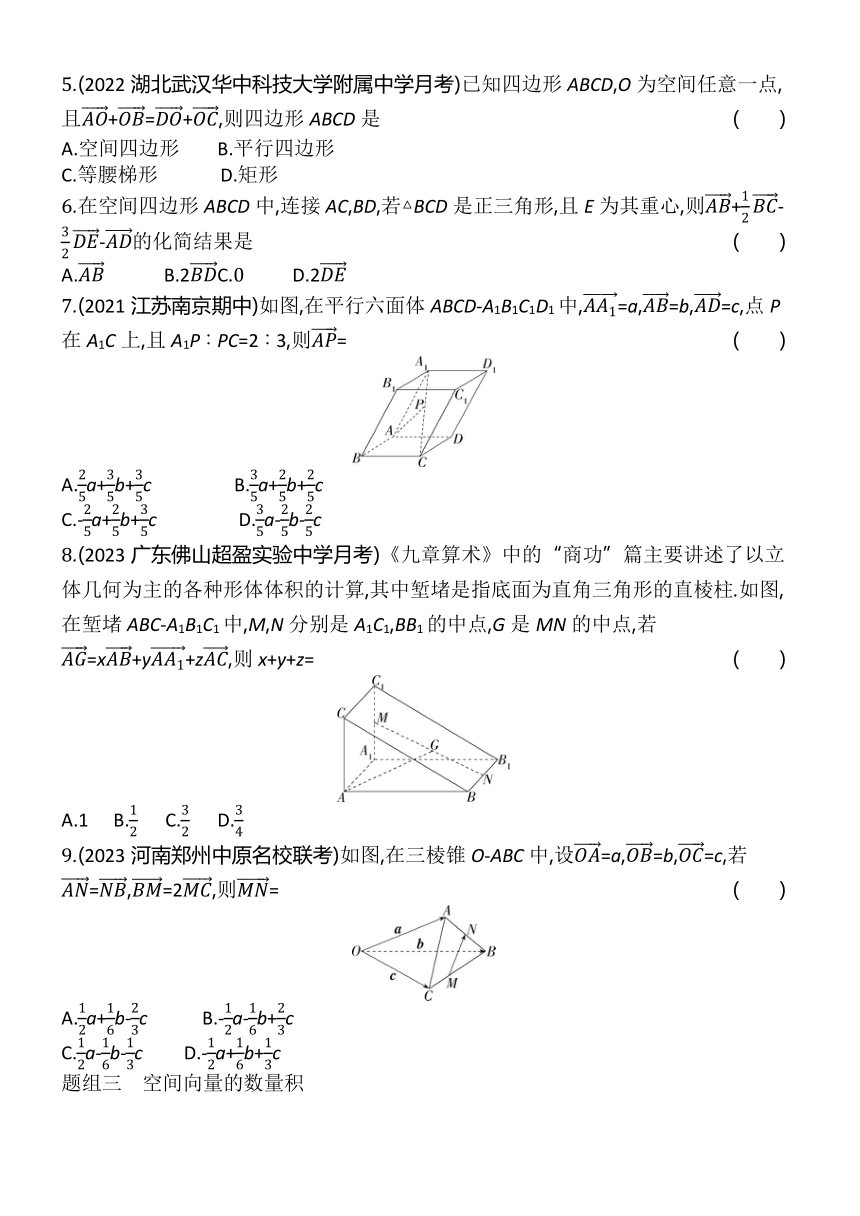
5.(2022湖北武汉华中科技大学附属中学月考)已知四边形ABCD,O为空间任意一点,且+=+,则四边形ABCD是 ( )
A.空间四边形 B.平行四边形
C.等腰梯形 D.矩形
6.在空间四边形ABCD中,连接AC,BD,若△BCD是正三角形,且E为其重心,则+--的化简结果是 ( )
A. B.2 C.0 D.2
7.(2021江苏南京期中)如图,在平行六面体ABCD-A1B1C1D1中,=a,=b,=c,点P在A1C上,且A1P∶PC=2∶3,则= ( )
A.a+b+c B.a+b+c
C.-a+b+c D.a-b-c
8.(2023广东佛山超盈实验中学月考)《九章算术》中的“商功”篇主要讲述了以立体几何为主的各种形体体积的计算,其中堑堵是指底面为直角三角形的直棱柱.如图,在堑堵ABC-A1B1C1中,M,N分别是A1C1,BB1的中点,G是MN的中点,若=x+y+z,则x+y+z= ( )
A.1 B. C. D.
9.(2023河南郑州中原名校联考)如图,在三棱锥O-ABC中,设=a,=b,=c,若=,=2,则= ( )
A.a+b-c B.-a-b+c
C.a-b-c D.-a+b+c
题组三 空间向量的数量积
10.(2023湖南长沙雅礼中学月考)如图,空间四边形ABCD的每条边和对角线长都等于1,F,G分别是AD,CD的中点,则·= ( )
A. B. C. D.
11.(2022北京理工大附中开学考试)已知空间向量a,b,若|a|=1,|b|=2,c=a+b,且c⊥a,则向量a与b的夹角为 ( )
A.30° B.60°
C.120° D.150°
12.(2023浙江温州金乡卫城中学月考)已知|a|=2,|b|=3,=60°,则|2a-3b|等于 ( )
A. B.97 C. D.61
13.已知|a|=1,|b|=,a与b的夹角为45°,若c=a+b,d=a-b,则c在d上的投影数量为 ( )
A. B.- C.1 D.-1
14.(2021河北张家口尚义第一中学期中)已知e1,e2是夹角为60°的两个单位向量,则a=e1+e2与b=e1-2e2的夹角是 ( )
A.120° B.60° C.30° D.45°
15.(2021辽宁朝阳第一高级中学期中)在底面是正方形的四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,∠A1AD=∠A1AB=,则||= ( )
A.2 B.2
C.3 D.
16.(2022河北石家庄一中期末)在空间四边形ABCD中,·+·+·= ( )
A.-1 B.0
C.1 D.不确定
17.已知|a|=3,|b|=4,m=a+b,n=a+λb,=135°,m⊥n,则λ= .
18.已知|a|=4,|b|=8,a与b的夹角是120°,当a+2b与ka-b的夹角为钝角时,实数k的取值范围为 .
能力提升练
题组 空间向量的数量积
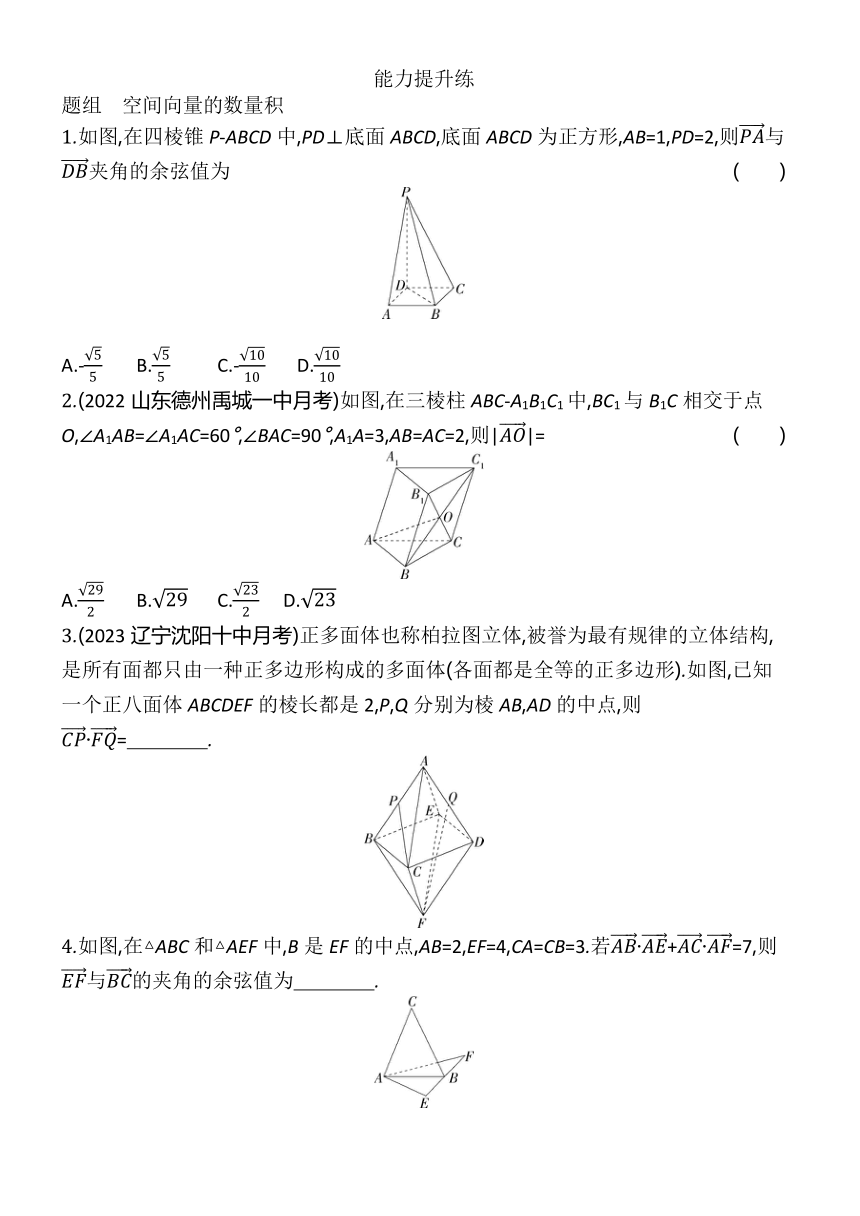
1.如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,AB=1,PD=2,则与夹角的余弦值为 ( )
A.- B. C.- D.
2.(2022山东德州禹城一中月考)如图,在三棱柱ABC-A1B1C1中,BC1与B1C相交于点O,∠A1AB=∠A1AC=60°,∠BAC=90°,A1A=3,AB=AC=2,则||= ( )
A. B. C. D.
3.(2023辽宁沈阳十中月考)正多面体也称柏拉图立体,被誉为最有规律的立体结构,是所有面都只由一种正多边形构成的多面体(各面都是全等的正多边形).如图,已知一个正八面体ABCDEF的棱长都是2,P,Q分别为棱AB,AD的中点,则·= .
4.如图,在△ABC和△AEF中,B是EF的中点,AB=2,EF=4,CA=CB=3.若·+·=7,则与的夹角的余弦值为 .
5.(2022安徽合肥六中月考)如图所示,在平面角为120°的二面角α-AB-β中,AC α,BD β,且AC⊥AB,BD⊥AB,垂足分别为A,B,AC=AB=BD=6,则||= .
6.(2023辽宁省实验中学月考)如图,在平行六面体ABCD-A1B1C1D1中,∠A1AD=∠A1AB=∠BAD=60°,AB=AD=2,AA1=1,P为线段BC的中点.
(1)求||;
(2)求与夹角的余弦值.
第一章 空间向量与立体几何
1.1 空间向量及其运算
1.1.1 空间向量及其运算
基础过关练
1.D 2.D 3.C 4.C 5.B 6.C 7.B 8.C
9.A 10.B 11.C 12.C 13.D 14.A 15.D 16.B
1.D 与的长度相等,方向相反,故=-,A错误;无法确定||,||的大小,故B错误;与不是共线向量,但可以平移到同一平面上,是共面向量,故C错误,D正确.
2.D 两个空间向量相等,则其模相等且方向相同,与表示它们的有向线段的起点和终点的位置无关,故A中说法错误;向量的模可以比较大小,但向量不能比较大小,故B中说法错误;空间四边形ABCD中,,不共线,模也不一定相等,故C中说法错误;同一条直线上的单位向量的模相等,但方向相同或相反,故不一定相等,故D中说法正确.
3.C 将空间中所有的单位向量的起点平移到同一个点,则它们的终点构成一个球面,故A中说法错误;两个向量相等不仅要保证模相等,还要保证方向相同,但a与b的方向不一定相同,故B中说法错误;向量的相等具有传递性,故C中说法正确;向量的平行不具有传递性,若b=0,则a与b共线,b与c共线,但a与c不一定共线,故D中说法错误.
4.C --=-=,①不符合;+-=+-=+=,②不符合;-+=+=,③符合;-+=-+=,④符合.故选C.
5.B 由已知可得=,由相等向量的定义可知,四边形ABCD的一组对边平行且相等,所以四边形ABCD是平行四边形,无法判断其是不是矩形.故选B.
6.C 如图所示,取BC的中点F,连接DF,AF,则=,又E为正三角形BCD的重心,即DF上靠近F的三等分点,所以=,则+--=+--=+-=-=0.
7.B 连接AC.因为A1P∶PC=2∶3,所以=,所以=+=+=+(-)=+=+(+)=++,又=a,=b,=c,所以=a+b+c.故选B.
8.C 连接AM,AN. ∵G是MN的中点,∴=(+)==++,∴x=,y=,z=,∴x+y+z=.故选C.
9.A 连接OM,ON,则=-=(+)-(+)=(+)--=(+)--(-)=+-=a+b-c.故选A.
10.B 由题意,得=,所以·=·=×1×1×cos 60°=.故选B.
11.C 设向量a与b的夹角为θ.∵c⊥a,∴c·a=(a+b)·a=0,则|a|2+|a||b|cos θ=0,∴cos θ=-,
∴θ=120°.
12.C |2a-3b|2=4a2-12a·b+9b2 =4×22-12×2×3×cos 60°+9×32=61,∴|2a-3b|=.
13.D 由题意得a·b=1××cos 45°=1,|d|===1,c·d=a2-b2=-1,因此c在d上的投影数量为=-1.故选D.
14.A 由题意得a·b=(e1+e2)·(e1-2e2)=-e1·e2-2=1-1×1×-2=-,|a|=====,|b|=====.
∴cos===-,∴=120°.
15.D ||2=|++|2=||2+||2+||2+2·+2·+2· =12+12+22+2×1×1×cos +2×1×2×cos +2×1×2×cos =1+1+4+2+2=10,∴||=.故选D.
16.B 令=a,=b,=c,则·+·+·=a·(c-b)+b·(a-c)+c·(b-a)=a·c-a·b+b·a-b·c+c·b-c·a=0.
17.答案 -
解析 由m⊥n得(a+b)·(a+λb)=0,∴a2+(1+λ)a·b+λb2=0,∴18+(λ+1)×3×4cos 135°+16λ=0,即2λ+3=0,∴λ=-.
18.答案 k>-7且k≠-
解析 由题意得(a+2b)·(ka-b)=ka2+(2k-1)a·b-2b2=16k+(2k-1)×4×8×cos 120°-128=-16k-112<0,解得k>-7.
又当k=-时,a+2b与ka-b反向共线,
∴k>-7且k≠-.
名师点睛 两向量a,b的夹角为锐角时,a·b>0,但a·b>0时,a,b的夹角为锐角或零角;两向量a,b的夹角为钝角时,a·b<0,但a·b<0时,a,b的夹角为钝角或平角.故在实际解题中,要考虑两向量同向、反向的情形.
能力提升练
1.D ∵PD⊥平面ABCD,DA,DC 平面ABCD,
∴PD⊥DA,PD⊥DC.
∵底面ABCD为正方形,∴DA⊥DC.
易知=-,=+,
∴·=(-)·(+)=+·-·-·=1,
||====,
||====,
∴cos<,>===.
2.A ∵四边形BCC1B1是平行四边形,
∴==(+),
∴=+=++=+(-)+=++.
∵∠A1AB=∠A1AC=60°,∠BAC=90°,A1A=3,AB=AC=2,
∴==4,=9,·=0,
·=·=2×3×cos 60°=3,
∴||2==(+++2·+2·+2·)=,
∴||=.故选A.
3.答案 1
解析 因为P为AB的中点,所以=(+).
因为=++=++(-)=--++(-)=--,
所以·=·=-+·-·-·=×22-×22=1.
4.答案
解析 由题意得=9=(-)2=+-2·=9+4-2·,所以·=2.由·+·=7,可得·(+)+·(+)=+·+·+·=4+·(-)+2+·=6+·(-)=6+·=7,所以·=2,即4×3×cos<,>=2,所以cos<,>=.
5.答案 12
解析 ∵AC⊥AB,BD⊥AB,
∴·=0,·=0.
∵二面角α-AB-β的平面角为120°,
∴<,>=180°-120°=60°.
∴=(++)2=+++2·+2·+2·=3×62+2×62×cos 60°=144,
∴||=12.
6.解析 (1)连接AP,AD1,∵=-=(+)-(+)=--,
∴||2==||2++||2-·-2·+·=4+1+1-2-2+1=3,
∴||=.
(2)由(1)知,=--,||=.
∵=+,∴||====,
·=(+)·=||2-·-·+·-·-||2=||2-·-·-||2=4-1--1=,
∴cos<,>===.
1.1 空间向量及其运算
1.1.1 空间向量及其运算
基础过关练
题组一 空间向量的概念
1.如图,在长方体ABCD-A'B'C'D'中,下列说法正确的是 ( )
A.=
B.||=||
C.向量与共线
D.向量与共面
2.(2022重庆开州中学月考)下列说法正确的是( )
A.若两个空间向量相等,则表示它们的有向线段的起点相同,终点也相同
B.若向量,满足||>||,且与同向,则>
C.空间四边形ABCD中,,为相反向量
D.同一条直线上的单位向量不一定相等
3.(2023北京首师大附属密云中学段考)下列说法正确的是 ( )
A.将空间中所有的单位向量的起点平移到同一个点,则它们的终点构成一个圆
B.若空间向量a,b满足|a|=|b|,则a=b
C.若空间向量m,n,p满足m=n,n=p,则m=p
D.若a与b共线,b与c共线,则a与c共线
题组二 空间向量的线性运算
4.(2022山东济宁邹城二中月考)在正方体ABCD-A1B1C1D1中,下列各式的运算结果为向量的是 ( )
①--;
②+-;
③-+;
④-+.
A.①② B.②③
C.③④ D.①④
5.(2022湖北武汉华中科技大学附属中学月考)已知四边形ABCD,O为空间任意一点,且+=+,则四边形ABCD是 ( )
A.空间四边形 B.平行四边形
C.等腰梯形 D.矩形
6.在空间四边形ABCD中,连接AC,BD,若△BCD是正三角形,且E为其重心,则+--的化简结果是 ( )
A. B.2 C.0 D.2
7.(2021江苏南京期中)如图,在平行六面体ABCD-A1B1C1D1中,=a,=b,=c,点P在A1C上,且A1P∶PC=2∶3,则= ( )
A.a+b+c B.a+b+c
C.-a+b+c D.a-b-c
8.(2023广东佛山超盈实验中学月考)《九章算术》中的“商功”篇主要讲述了以立体几何为主的各种形体体积的计算,其中堑堵是指底面为直角三角形的直棱柱.如图,在堑堵ABC-A1B1C1中,M,N分别是A1C1,BB1的中点,G是MN的中点,若=x+y+z,则x+y+z= ( )
A.1 B. C. D.
9.(2023河南郑州中原名校联考)如图,在三棱锥O-ABC中,设=a,=b,=c,若=,=2,则= ( )
A.a+b-c B.-a-b+c
C.a-b-c D.-a+b+c
题组三 空间向量的数量积
10.(2023湖南长沙雅礼中学月考)如图,空间四边形ABCD的每条边和对角线长都等于1,F,G分别是AD,CD的中点,则·= ( )
A. B. C. D.
11.(2022北京理工大附中开学考试)已知空间向量a,b,若|a|=1,|b|=2,c=a+b,且c⊥a,则向量a与b的夹角为 ( )
A.30° B.60°
C.120° D.150°
12.(2023浙江温州金乡卫城中学月考)已知|a|=2,|b|=3,
A. B.97 C. D.61
13.已知|a|=1,|b|=,a与b的夹角为45°,若c=a+b,d=a-b,则c在d上的投影数量为 ( )
A. B.- C.1 D.-1
14.(2021河北张家口尚义第一中学期中)已知e1,e2是夹角为60°的两个单位向量,则a=e1+e2与b=e1-2e2的夹角是 ( )
A.120° B.60° C.30° D.45°
15.(2021辽宁朝阳第一高级中学期中)在底面是正方形的四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,∠A1AD=∠A1AB=,则||= ( )
A.2 B.2
C.3 D.
16.(2022河北石家庄一中期末)在空间四边形ABCD中,·+·+·= ( )
A.-1 B.0
C.1 D.不确定
17.已知|a|=3,|b|=4,m=a+b,n=a+λb,
18.已知|a|=4,|b|=8,a与b的夹角是120°,当a+2b与ka-b的夹角为钝角时,实数k的取值范围为 .
能力提升练
题组 空间向量的数量积
1.如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,AB=1,PD=2,则与夹角的余弦值为 ( )
A.- B. C.- D.
2.(2022山东德州禹城一中月考)如图,在三棱柱ABC-A1B1C1中,BC1与B1C相交于点O,∠A1AB=∠A1AC=60°,∠BAC=90°,A1A=3,AB=AC=2,则||= ( )
A. B. C. D.
3.(2023辽宁沈阳十中月考)正多面体也称柏拉图立体,被誉为最有规律的立体结构,是所有面都只由一种正多边形构成的多面体(各面都是全等的正多边形).如图,已知一个正八面体ABCDEF的棱长都是2,P,Q分别为棱AB,AD的中点,则·= .
4.如图,在△ABC和△AEF中,B是EF的中点,AB=2,EF=4,CA=CB=3.若·+·=7,则与的夹角的余弦值为 .
5.(2022安徽合肥六中月考)如图所示,在平面角为120°的二面角α-AB-β中,AC α,BD β,且AC⊥AB,BD⊥AB,垂足分别为A,B,AC=AB=BD=6,则||= .
6.(2023辽宁省实验中学月考)如图,在平行六面体ABCD-A1B1C1D1中,∠A1AD=∠A1AB=∠BAD=60°,AB=AD=2,AA1=1,P为线段BC的中点.
(1)求||;
(2)求与夹角的余弦值.
第一章 空间向量与立体几何
1.1 空间向量及其运算
1.1.1 空间向量及其运算
基础过关练
1.D 2.D 3.C 4.C 5.B 6.C 7.B 8.C
9.A 10.B 11.C 12.C 13.D 14.A 15.D 16.B
1.D 与的长度相等,方向相反,故=-,A错误;无法确定||,||的大小,故B错误;与不是共线向量,但可以平移到同一平面上,是共面向量,故C错误,D正确.
2.D 两个空间向量相等,则其模相等且方向相同,与表示它们的有向线段的起点和终点的位置无关,故A中说法错误;向量的模可以比较大小,但向量不能比较大小,故B中说法错误;空间四边形ABCD中,,不共线,模也不一定相等,故C中说法错误;同一条直线上的单位向量的模相等,但方向相同或相反,故不一定相等,故D中说法正确.
3.C 将空间中所有的单位向量的起点平移到同一个点,则它们的终点构成一个球面,故A中说法错误;两个向量相等不仅要保证模相等,还要保证方向相同,但a与b的方向不一定相同,故B中说法错误;向量的相等具有传递性,故C中说法正确;向量的平行不具有传递性,若b=0,则a与b共线,b与c共线,但a与c不一定共线,故D中说法错误.
4.C --=-=,①不符合;+-=+-=+=,②不符合;-+=+=,③符合;-+=-+=,④符合.故选C.
5.B 由已知可得=,由相等向量的定义可知,四边形ABCD的一组对边平行且相等,所以四边形ABCD是平行四边形,无法判断其是不是矩形.故选B.
6.C 如图所示,取BC的中点F,连接DF,AF,则=,又E为正三角形BCD的重心,即DF上靠近F的三等分点,所以=,则+--=+--=+-=-=0.
7.B 连接AC.因为A1P∶PC=2∶3,所以=,所以=+=+=+(-)=+=+(+)=++,又=a,=b,=c,所以=a+b+c.故选B.
8.C 连接AM,AN. ∵G是MN的中点,∴=(+)==++,∴x=,y=,z=,∴x+y+z=.故选C.
9.A 连接OM,ON,则=-=(+)-(+)=(+)--=(+)--(-)=+-=a+b-c.故选A.
10.B 由题意,得=,所以·=·=×1×1×cos 60°=.故选B.
11.C 设向量a与b的夹角为θ.∵c⊥a,∴c·a=(a+b)·a=0,则|a|2+|a||b|cos θ=0,∴cos θ=-,
∴θ=120°.
12.C |2a-3b|2=4a2-12a·b+9b2 =4×22-12×2×3×cos 60°+9×32=61,∴|2a-3b|=.
13.D 由题意得a·b=1××cos 45°=1,|d|===1,c·d=a2-b2=-1,因此c在d上的投影数量为=-1.故选D.
14.A 由题意得a·b=(e1+e2)·(e1-2e2)=-e1·e2-2=1-1×1×-2=-,|a|=====,|b|=====.
∴cos
15.D ||2=|++|2=||2+||2+||2+2·+2·+2· =12+12+22+2×1×1×cos +2×1×2×cos +2×1×2×cos =1+1+4+2+2=10,∴||=.故选D.
16.B 令=a,=b,=c,则·+·+·=a·(c-b)+b·(a-c)+c·(b-a)=a·c-a·b+b·a-b·c+c·b-c·a=0.
17.答案 -
解析 由m⊥n得(a+b)·(a+λb)=0,∴a2+(1+λ)a·b+λb2=0,∴18+(λ+1)×3×4cos 135°+16λ=0,即2λ+3=0,∴λ=-.
18.答案 k>-7且k≠-
解析 由题意得(a+2b)·(ka-b)=ka2+(2k-1)a·b-2b2=16k+(2k-1)×4×8×cos 120°-128=-16k-112<0,解得k>-7.
又当k=-时,a+2b与ka-b反向共线,
∴k>-7且k≠-.
名师点睛 两向量a,b的夹角为锐角时,a·b>0,但a·b>0时,a,b的夹角为锐角或零角;两向量a,b的夹角为钝角时,a·b<0,但a·b<0时,a,b的夹角为钝角或平角.故在实际解题中,要考虑两向量同向、反向的情形.
能力提升练
1.D ∵PD⊥平面ABCD,DA,DC 平面ABCD,
∴PD⊥DA,PD⊥DC.
∵底面ABCD为正方形,∴DA⊥DC.
易知=-,=+,
∴·=(-)·(+)=+·-·-·=1,
||====,
||====,
∴cos<,>===.
2.A ∵四边形BCC1B1是平行四边形,
∴==(+),
∴=+=++=+(-)+=++.
∵∠A1AB=∠A1AC=60°,∠BAC=90°,A1A=3,AB=AC=2,
∴==4,=9,·=0,
·=·=2×3×cos 60°=3,
∴||2==(+++2·+2·+2·)=,
∴||=.故选A.
3.答案 1
解析 因为P为AB的中点,所以=(+).
因为=++=++(-)=--++(-)=--,
所以·=·=-+·-·-·=×22-×22=1.
4.答案
解析 由题意得=9=(-)2=+-2·=9+4-2·,所以·=2.由·+·=7,可得·(+)+·(+)=+·+·+·=4+·(-)+2+·=6+·(-)=6+·=7,所以·=2,即4×3×cos<,>=2,所以cos<,>=.
5.答案 12
解析 ∵AC⊥AB,BD⊥AB,
∴·=0,·=0.
∵二面角α-AB-β的平面角为120°,
∴<,>=180°-120°=60°.
∴=(++)2=+++2·+2·+2·=3×62+2×62×cos 60°=144,
∴||=12.
6.解析 (1)连接AP,AD1,∵=-=(+)-(+)=--,
∴||2==||2++||2-·-2·+·=4+1+1-2-2+1=3,
∴||=.
(2)由(1)知,=--,||=.
∵=+,∴||====,
·=(+)·=||2-·-·+·-·-||2=||2-·-·-||2=4-1--1=,
∴cos<,>===.
