1.1.3 空间向量的坐标与空间直角坐标系 同步练习-2023-2024学年高二上学期数学人教B版(2019)选择性必修第一册(含解析)
文档属性
| 名称 | 1.1.3 空间向量的坐标与空间直角坐标系 同步练习-2023-2024学年高二上学期数学人教B版(2019)选择性必修第一册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 15:57:58 | ||
图片预览




文档简介
1.1.3 空间向量的坐标与空间直角坐标系
基础过关练
题组一 空间向量的坐标
1.已知{e1,e2,e3}是单位正交基底,下列说法正确的是 ( )
A.若p=2e1-e2+3e3,则p=(2,1,3)
B.若q=-e1+2e2,则q=(-1,2)
C.若r=e1+3e2-e3,则r=(1,3,-1)
D.若s=-3e2,则s=(0,0,-3)
2.(2022北京昌平新学道临川学校月考)已知{a,b,c}是空间向量的一组基底,{a+b,a-b,c}是空间向量的另外一组基底,若一向量p在基底{a,b,c}下的坐标为(1,2,3),则向量p在基底{a+b,a-b,c}下的坐标为 ( )
A. B.
C. D.
题组二 空间向量坐标的运算
3.(2023北京三中期中)若向量a=(2,0,-1),b=(0,1,-2),则2a-b= ( )
A.(-4,1,0) B.(-4,1,-4)
C.(4,-1,0) D.(4,-1,-4)
4.若a=(x,2,0),b=(3,2-x,x2),且a与b的夹角为钝角,则实数x的取值范围是 ( )
A.x>4 B.x<-4 C.05.(2021天津静海检测)若向量a=(1,1,2),b=(1,2,1),c=(1,1,1),则(c-a)·2b= .
6.(2023北京师范大学附属中学期中)若a=(1,0,-1),b=(0,2,1),c=(2,m,-1)为共面向量,则m= .
题组三 利用空间向量的坐标运算解决平行、
垂直问题
7.若在△ABC中,∠C=90°,A(1,2,-3k),B(-2,1,0),C(4,0,-2k),则k的值为 ( )
A. B.-
C.2 D.±
8.已知在空间直角坐标系中,O为坐标原点,A(4,1,3),B(2,-5,1),若C为线段AB上一点,且=,则点C的坐标为 ( )
A. B.
C. D.
9.(2023辽宁省实验中学月考)已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a=,b=.
(1)若向量ka+b,ka-2b互相垂直,求实数k的值;
(2)若向量λa-b,a-λb共线,求实数λ的值.
题组四 利用空间向量的坐标运算解决夹角、模
(长度)问题
10.(2021江苏连云港期末)已知空间中三点A(0,2,3),B(-2,1,6),C(1,-1,5),向量a=(m,-1,n),且向量a分别与向量,垂直,则|a|= ( )
A.4 B.2 C.2 D.
11.(2022山东济宁期中)已知空间中三点A(-2,0,8),P(m,m,m),B(4,-4,6),若向量与的夹角为60°,则实数m= ( )
A.1 B.2 C.-1 D.-2
12.(2023山东烟台招远二中月考)若空间向量a=(3,0,4),b=(-3,2,5),则向量b在向量a上的投影数量为 .
13.(2022黑龙江鸡西虎林实验高级中学期末)已知点A(0,1,2),B(1,-1,3),C(1,5,-1).
(1)若D为线段BC的中点,求||;
(2)若=(2,a,1),且·=1,求a的值,并求此时向量与夹角的余弦值.
题组五 空间直角坐标系及其应用
14.(2022黑龙江绥化肇东四中期中)已知点A(1,1,-3),B(3,1,-1),则线段AB的中点M关于平面yOz对称的点的坐标为 ( )
A.(-2,1,-2) B.(2,1,-2)
C.(2,-1,-2) D.(2,1,2)
15.在空间直角坐标系中,已知M(-1,0,2),N(3,2,-4),则线段MN的中点Q与坐标原点O之间的距离为 ( )
A. B. C.2 D.3
16.一个正方体截下的一角P-ABC如图所示,其中PA=a,PB=b,PC=c.建立空间直角坐标系,则△ABC的重心G的坐标是 .
17.已知正三棱柱ABC-A1B1C1中,AB=2,AB1⊥BC1,点O,O1分别是AC,A1C1的中点,建立如图所示的空间直角坐标系.
(1)求正三棱柱的侧棱长;
(2)求与夹角的余弦值.
能力提升练
题组一 空间向量坐标的应用
1.(2023山东聊城二中月考)已知a=(x,4,1),b=(-2,y,-1),c=(3,-2,z),若a∥b,b⊥c,则a+c与b+c夹角的余弦值为 ( )
A.- B.
C. D.-
2.(2022辽宁大连一中月考)在空间直角坐标系中,O(0,0,0),E(2,0,0),F(0,2,0),B为EF的中点,C为空间中一点且满足||=||=3,若cos<,>=,则·= ( )
A.9 B.7 C.5 D.3
3.已知O为坐标原点,向量=(1,2,3),=(2,1,2),=(1,1,2),点Q在直线OP上运动,则当·取得最小值时,点Q的坐标为 ( )
A. B.
C. D.
4.(2022河南濮阳范县一中月考)已知向量a=(1,1,0),b=(-1,0,2),若向量a+kb与2a+b所成的角为锐角,则实数k的取值范围为 .
5.已知=(1,5,-2),=(3,1,z),若⊥,=(x-1,y,-3),且BP⊥平面ABC,则x+y= .
6.(2022福建福州三中月考)已知空间中三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)若点D在直线AC上,且⊥,求点D的坐标;
(2)求以BA,BC为邻边的平行四边形的面积.
题组二 空间直角坐标系的应用
7.三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,N是BC的中点,=λ(λ∈R),=3,若⊥,则λ= ( )
A. B.
C. D.
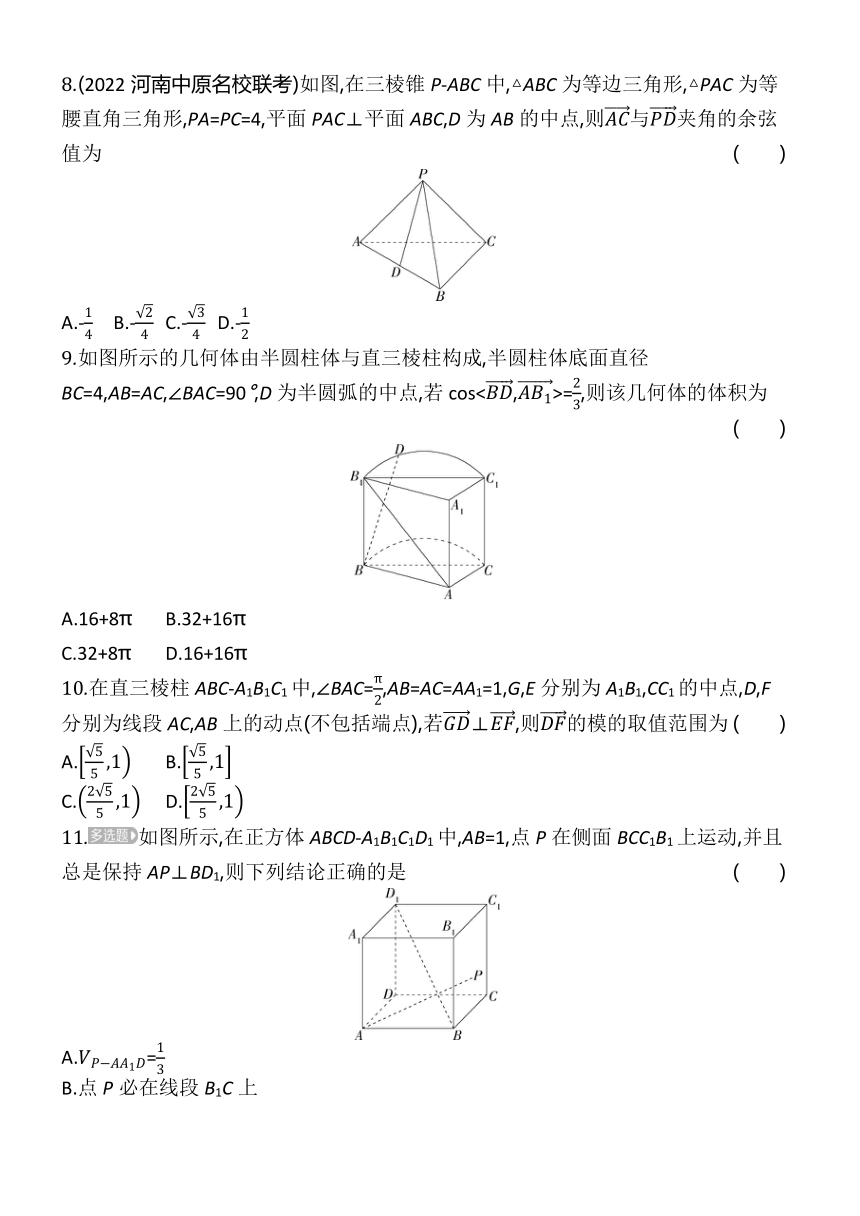
8.(2022河南中原名校联考)如图,在三棱锥P-ABC中,△ABC为等边三角形,△PAC为等腰直角三角形,PA=PC=4,平面PAC⊥平面ABC,D为AB的中点,则与夹角的余弦值为 ( )
A.- B.- C.- D.-
9.如图所示的几何体由半圆柱体与直三棱柱构成,半圆柱体底面直径BC=4,AB=AC,∠BAC=90°,D为半圆弧的中点,若cos<,>=,则该几何体的体积为 ( )
A.16+8π B.32+16π
C.32+8π D.16+16π
10.在直三棱柱ABC-A1B1C1中,∠BAC=,AB=AC=AA1=1,G,E分别为A1B1,CC1的中点,D,F分别为线段AC,AB上的动点(不包括端点),若⊥,则的模的取值范围为 ( )
A. B.
C. D.
11.如图所示,在正方体ABCD-A1B1C1D1中,AB=1,点P在侧面BCC1B1上运动,并且总是保持AP⊥BD1,则下列结论正确的是 ( )
A.=
B.点P必在线段B1C上
C.AP⊥BC1
D.AP∥平面A1C1D
12.在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱AA1⊥底面ABCD.已知AB=1,AA1=,E为线段AB上的一个动点,则|D1E|+|CE|的最小值为 ( )
A.2 B.
C.+1 D.2+
13.如图,以棱长为1的正方体的三条棱所在直线为坐标轴,建立空间直角坐标系Oxyz,点P在线段AB上,点Q在线段DC上.
(1)当PB=2AP,且点P关于y轴的对称点为M时,求|PM|;
(2)当点P是AB的中点,点Q在DC上运动时,探究|PQ|的最小值.
1.1.3 空间向量的坐标与空间直角坐标系
基础过关练
1.C 2.B 3.C 4.B 7.D 8.C 10.D 11.B
14.A 15.A
1.C 由空间向量的坐标的概念可知p=(2,-1,3),q=(-1,2,0),r=(1,3,-1),s=(0,-3,0).
2.B 设向量p在基底{a+b,a-b,c}下的坐标为(x,y,z),则p=a+2b+3c=x(a+b)+y(a-b)+zc=(x+y)a+(x-y)b+zc,所以解得故p在基底{a+b,a-b,c}下的坐标为.
3.C 因为向量a=(2,0,-1),所以2a=(4,0,-2),又向量b=(0,1,-2),所以2a-b=(4,0,-2)-(0,1,-2)=(4,-1,0).故选C.
4.B 由题意可知,a·b=3x+2(2-x)<0,解得x<-4,易知a,b不共线,故选B.
5.答案 -2
解析 易得c-a=(0,0,-1),2b=(2,4,2),∴(c-a)·2b=0+0-2=-2.
6.答案 2
解析 因为a,b,c为共面向量,所以存在唯一的实数对(λ,μ),使得c=λa+μb,即(2,m,-1)=λ(1,0,-1)+μ(0,2,1),所以解得
7.D 由题意得=(-6,1,2k),=(-3,2,-k).
∵∠C=90°,∴⊥,∴·=-6×(-3)+1×2+2k×(-k)=-2k2+20=0,∴k=±.故选D.
8.C ∵C为线段AB上一点,且=,∴=,设C(x,y,z),则(x-4,y-1,z-3)=(-2,-6,-2)=,
∴解得∴C.故选C.
9.解析 (1)根据题意,得a=(1,1,0),b=(-1,0,2),则ka+b=(k-1,k,2),ka-2b=(k+2,k,-4).
若向量ka+b,ka-2b互相垂直,则(ka+b)·(ka-2b)=(k-1,k,2)·(k+2,k,-4)=(k-1)(k+2)+k2-8=0,∴2k2+k-10=0,解得k=-或k=2.
(2)由(1)知,a=(1,1,0),b=(-1,0,2),则λa-b=(λ+1,λ,-2),a-λb=(1+λ,1,-2λ).
由向量λa-b,a-λb共线,可设λa-b=μ(a-λb),μ∈R,则解得λ=μ=±1.
10.D 由题意得=(-2,-1,3),=(1,-3,2).
因为向量a分别与向量,垂直,
所以即
解得故a=(-1,-1,-1),
因此|a|==.故选D.
11.B ∵A(-2,0,8),P(m,m,m),B(4,-4,6),
∴=(-2-m,-m,8-m),=(4-m,-4-m,6-m),
由题意得cos 60°=
=,
∴m2-4m+4=0,∴m=2.
12.答案
解析 由题意得a·b=-9+0+20=11,|a|=5,所以向量b在向量a上的投影数量为=.
13.解析 (1)由题意得D(1,2,1),∴=(1,1,-1),∴||==.
(2)易知=(1,-2,1),∴·=2-2a+1=1,解得a=1,∴=(2,1,1),
∴cos<,>===,
即向量与夹角的余弦值为.
14.A 由题意得M(2,1,-2),∴点M关于平面yOz对称的点的坐标为(-2,1,-2).故选A.
15.A ∵M(-1,0,2),N(3,2,-4),∴线段MN的中点Q的坐标为(1,1,-1),∴点Q与坐标原点O之间的距离|QO|==.故选A.
16.答案
解析 由题意知,A(a,0,0),B(0,b,0),C(0,0,c).由重心坐标公式得点G的坐标为.
17.解析 (1)设正三棱柱的侧棱长为h.
由题意得A(0,-1,0),B(,0,0),C(0,1,0),B1(,0,h),C1(0,1,h),则=(,1,h),=(-,1,h).因为AB1⊥BC1,所以·=-3+1+h2=0,解得h=(负值舍去).故正三棱柱的侧棱长为.
(2)由(1)可知=(,1,),=(-,1,0),
所以·=-3+1=-2,||=,||=2,
所以cos<,>==-.
能力提升练
1.A 2.D 3.C 7.C 8.B 9.A 10.A 11.BD
12.B
1.A 因为a∥b,所以==,解得x=2,y=-4,所以a=(2,4,1),b=(-2,-4,-1).
因为b⊥c,所以b·c=0,即-6+8-z=0,解得z=2,所以c=(3,-2,2),
所以a+c=(5,2,3),b+c=(1,-6,1),
所以(a+c)·(b+c)=5-12+3=-4,|a+c|==,|b+c|==.
设a+c与b+c的夹角为θ,则cos===-.故选A.
2.D 易得B(,,0),设C(x,y,z),则=(x,y,z),=(x-,y-,z),=(-2,2,0),
由cos<,>=
==,
整理可得x-y=-①.
由||=||=3,得=,化简得x+y=②.
联立①②,解得x=,y=,则·=·(0,2,0)=3.
故选D.
3.C ∵点Q在直线OP上运动,∴O,P,Q三点共线,∴存在唯一的实数λ,使得=λ=(λ,λ,2λ),
∴=(1-λ,2-λ,3-2λ),=(2-λ,1-λ,2-2λ),
∴·=(1-λ)(2-λ)+(2-λ)(1-λ)+(3-2λ)·(2-2λ)=6λ2-16λ+10=6-,
当且仅当λ=时,上式取得最小值,
此时点Q的坐标为.故选C.
4.答案
解析 易得a+kb=(1-k,1,2k),2a+b=(1,2,2).
由题意得(a+kb)·(2a+b)>0且a+kb,2a+b不共线,
∴1-k+2+4k>0,且==不成立,解得k>-1且k≠,∴实数k的取值范围为.
5.答案
解析 由题意可得⊥,⊥,⊥.
利用向量数量积的运算公式,可得解得∴x+y=-=.
6.解析 (1)根据题意,得=(1,-3,2),由点D在直线AC上,可设=λ=λ(1,-3,2),λ∈R.
设O为坐标原点,则=+=(0,2,3)+λ(1,-3,2)=(λ,2-3λ,3+2λ),=-=(λ,2-3λ,3+2λ)-(-2,1,6)=(λ+2,1-3λ,2λ-3),
故·=(1,-3,2)·(λ+2,1-3λ,2λ-3)=λ+2-3+9λ+4λ-6=14λ-7=0,∴λ=,
∴=,∴D.
(2)根据题意,得=(2,1,-3),=(3,-2,-1),
∴||==,||==,
·=2×3+1×(-2)+(-3)×(-1)=7,
∴cos B=cos<,>===,∴sin B=,
∴平行四边形的面积为××=7,
故以BA,BC为邻边的平行四边形的面积为7.
7.C 如图,以AB,AC,AA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系Axyz,
则A1(0,0,1),B1(1,0,1),∴=(1,0,0),∴=(λ,0,0),则P(λ,0,1),又N,B(1,0,0),M,所以=,=,所以·=λ-+-=0,解得λ=.故选C.
8.B 取AC的中点O,连接OP,OB.
∵PA=PC,∴AC⊥OP.
∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,
∴OP⊥平面ABC.
∵AB=BC,
∴AC⊥OB.
以O为坐标原点,建立如图所示的空间直角坐标系,
∵△PAC是等腰直角三角形,PA=PC=4,△ABC为等边三角形,
∴A(2,0,0),C(-2,0,0),P(0,0,2),D(,,0),
∴=(-4,0,0),=(,,-2),
∴cos<,>===-.故选B.
9.A 如图,设D在底面半圆上的射影为D1,连接AD1,交BC于点O,连接A1D,交B1C1于点O1.
依题意知AD1⊥BC,A1D⊥B1C1,O,O1分别是下底面、上底面半圆的圆心.连接OO1,则OO1与上、下底面垂直,所以OO1⊥OB,OO1⊥OA.
以OB,OA,OO1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.设几何体的高为h(h>0),则B(2,0,0),D(0,-2,h),A(0,2,0),B1(2,0,h),所以=(-2,-2,h),=(2,-2,h).
所以cos<,>===,即=,所以h=4(负值舍去).所以几何体的体积为×π×22×4+×4×2×4=16+8π.故选A.
10.A 建立如图所示的空间直角坐标系Axyz,
则G,E,设D(0,y,0),F(x,0,0),其中x,y∈(0,1),则=,=,
∵⊥,∴·=0,即-x-y+=0,即x+2y=1,又∵0又||===,
∴当y=时,||min==;当y=0时,||=1;当y=时,||=,故的模的取值范围为.
11.BD ∵点P在侧面BCC1B1上运动,平面BCC1B1∥平面AA1D1D,∴点P到平面AA1D1D的距离即为点C到平面AA1D1D的距离,即为正方体的棱长,∴=·CD=××1×1×1=,故A中结论错误.
以D为坐标原点,建立如图所示的空间直角坐标系,
则A(1,0,0),B(1,1,0),D1(0,0,1),B1(1,1,1),C(0,1,0),∴=(-1,-1,1),=(-1,0,-1),设P(x,1,z)(0≤x≤1,0≤z≤1),则=(x-1,1,z).
∵AP⊥BD1,∴·=1-x-1+z=0,∴x=z,
∴P(x,1,x),∴=(x,0,x),∴=-x,即B1,P,C三点共线,∴点P必在线段B1C上,故B中结论正确.
易知C1(0,1,1),∴=(-1,0,1),又=(x-1,1,x),∴·=1-x+x=1,∴AP与BC1不垂直,故C中结论错误.
易知A1(1,0,1),D(0,0,0),∴=(-1,1,0),=(1,0,1),又=(x-1,1,x),∴=x+(其中0≤x≤1),∴,,共面,又AP 平面A1C1D,∴AP∥平面A1C1D,故D中结论正确.
故选BD.
12.B 建立如图所示的空间直角坐标系Axyz,
则D1(0,1,),C(1,1,0).
∵E为线段AB上的一个动点,
∴设E(t,0,0)(0≤t≤1),
则|D1E|==,|CE|=,
故问题转化为求y=+(0≤t≤1)的最小值,即转化为求平面直角坐标系tOy中的一个动点P(t,0)到两定点M(0,-2),N(1,1)的距离之和的最小值问题,如图所示:
由此可知,当M,P,N三点共线时,
=|MN|==,故=.
故选B.
13.解析 (1)由PB=2AP得P,
所以M,所以|PM|=
=.
(2)由题意得P.设点Q(a,1,a),a∈[0,1],则|PQ|===,所以当a=时,|PQ|取得最小值,此时点Q的坐标为.
基础过关练
题组一 空间向量的坐标
1.已知{e1,e2,e3}是单位正交基底,下列说法正确的是 ( )
A.若p=2e1-e2+3e3,则p=(2,1,3)
B.若q=-e1+2e2,则q=(-1,2)
C.若r=e1+3e2-e3,则r=(1,3,-1)
D.若s=-3e2,则s=(0,0,-3)
2.(2022北京昌平新学道临川学校月考)已知{a,b,c}是空间向量的一组基底,{a+b,a-b,c}是空间向量的另外一组基底,若一向量p在基底{a,b,c}下的坐标为(1,2,3),则向量p在基底{a+b,a-b,c}下的坐标为 ( )
A. B.
C. D.
题组二 空间向量坐标的运算
3.(2023北京三中期中)若向量a=(2,0,-1),b=(0,1,-2),则2a-b= ( )
A.(-4,1,0) B.(-4,1,-4)
C.(4,-1,0) D.(4,-1,-4)
4.若a=(x,2,0),b=(3,2-x,x2),且a与b的夹角为钝角,则实数x的取值范围是 ( )
A.x>4 B.x<-4 C.0
6.(2023北京师范大学附属中学期中)若a=(1,0,-1),b=(0,2,1),c=(2,m,-1)为共面向量,则m= .
题组三 利用空间向量的坐标运算解决平行、
垂直问题
7.若在△ABC中,∠C=90°,A(1,2,-3k),B(-2,1,0),C(4,0,-2k),则k的值为 ( )
A. B.-
C.2 D.±
8.已知在空间直角坐标系中,O为坐标原点,A(4,1,3),B(2,-5,1),若C为线段AB上一点,且=,则点C的坐标为 ( )
A. B.
C. D.
9.(2023辽宁省实验中学月考)已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a=,b=.
(1)若向量ka+b,ka-2b互相垂直,求实数k的值;
(2)若向量λa-b,a-λb共线,求实数λ的值.
题组四 利用空间向量的坐标运算解决夹角、模
(长度)问题
10.(2021江苏连云港期末)已知空间中三点A(0,2,3),B(-2,1,6),C(1,-1,5),向量a=(m,-1,n),且向量a分别与向量,垂直,则|a|= ( )
A.4 B.2 C.2 D.
11.(2022山东济宁期中)已知空间中三点A(-2,0,8),P(m,m,m),B(4,-4,6),若向量与的夹角为60°,则实数m= ( )
A.1 B.2 C.-1 D.-2
12.(2023山东烟台招远二中月考)若空间向量a=(3,0,4),b=(-3,2,5),则向量b在向量a上的投影数量为 .
13.(2022黑龙江鸡西虎林实验高级中学期末)已知点A(0,1,2),B(1,-1,3),C(1,5,-1).
(1)若D为线段BC的中点,求||;
(2)若=(2,a,1),且·=1,求a的值,并求此时向量与夹角的余弦值.
题组五 空间直角坐标系及其应用
14.(2022黑龙江绥化肇东四中期中)已知点A(1,1,-3),B(3,1,-1),则线段AB的中点M关于平面yOz对称的点的坐标为 ( )
A.(-2,1,-2) B.(2,1,-2)
C.(2,-1,-2) D.(2,1,2)
15.在空间直角坐标系中,已知M(-1,0,2),N(3,2,-4),则线段MN的中点Q与坐标原点O之间的距离为 ( )
A. B. C.2 D.3
16.一个正方体截下的一角P-ABC如图所示,其中PA=a,PB=b,PC=c.建立空间直角坐标系,则△ABC的重心G的坐标是 .
17.已知正三棱柱ABC-A1B1C1中,AB=2,AB1⊥BC1,点O,O1分别是AC,A1C1的中点,建立如图所示的空间直角坐标系.
(1)求正三棱柱的侧棱长;
(2)求与夹角的余弦值.
能力提升练
题组一 空间向量坐标的应用
1.(2023山东聊城二中月考)已知a=(x,4,1),b=(-2,y,-1),c=(3,-2,z),若a∥b,b⊥c,则a+c与b+c夹角的余弦值为 ( )
A.- B.
C. D.-
2.(2022辽宁大连一中月考)在空间直角坐标系中,O(0,0,0),E(2,0,0),F(0,2,0),B为EF的中点,C为空间中一点且满足||=||=3,若cos<,>=,则·= ( )
A.9 B.7 C.5 D.3
3.已知O为坐标原点,向量=(1,2,3),=(2,1,2),=(1,1,2),点Q在直线OP上运动,则当·取得最小值时,点Q的坐标为 ( )
A. B.
C. D.
4.(2022河南濮阳范县一中月考)已知向量a=(1,1,0),b=(-1,0,2),若向量a+kb与2a+b所成的角为锐角,则实数k的取值范围为 .
5.已知=(1,5,-2),=(3,1,z),若⊥,=(x-1,y,-3),且BP⊥平面ABC,则x+y= .
6.(2022福建福州三中月考)已知空间中三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)若点D在直线AC上,且⊥,求点D的坐标;
(2)求以BA,BC为邻边的平行四边形的面积.
题组二 空间直角坐标系的应用
7.三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,N是BC的中点,=λ(λ∈R),=3,若⊥,则λ= ( )
A. B.
C. D.
8.(2022河南中原名校联考)如图,在三棱锥P-ABC中,△ABC为等边三角形,△PAC为等腰直角三角形,PA=PC=4,平面PAC⊥平面ABC,D为AB的中点,则与夹角的余弦值为 ( )
A.- B.- C.- D.-
9.如图所示的几何体由半圆柱体与直三棱柱构成,半圆柱体底面直径BC=4,AB=AC,∠BAC=90°,D为半圆弧的中点,若cos<,>=,则该几何体的体积为 ( )
A.16+8π B.32+16π
C.32+8π D.16+16π
10.在直三棱柱ABC-A1B1C1中,∠BAC=,AB=AC=AA1=1,G,E分别为A1B1,CC1的中点,D,F分别为线段AC,AB上的动点(不包括端点),若⊥,则的模的取值范围为 ( )
A. B.
C. D.
11.如图所示,在正方体ABCD-A1B1C1D1中,AB=1,点P在侧面BCC1B1上运动,并且总是保持AP⊥BD1,则下列结论正确的是 ( )
A.=
B.点P必在线段B1C上
C.AP⊥BC1
D.AP∥平面A1C1D
12.在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱AA1⊥底面ABCD.已知AB=1,AA1=,E为线段AB上的一个动点,则|D1E|+|CE|的最小值为 ( )
A.2 B.
C.+1 D.2+
13.如图,以棱长为1的正方体的三条棱所在直线为坐标轴,建立空间直角坐标系Oxyz,点P在线段AB上,点Q在线段DC上.
(1)当PB=2AP,且点P关于y轴的对称点为M时,求|PM|;
(2)当点P是AB的中点,点Q在DC上运动时,探究|PQ|的最小值.
1.1.3 空间向量的坐标与空间直角坐标系
基础过关练
1.C 2.B 3.C 4.B 7.D 8.C 10.D 11.B
14.A 15.A
1.C 由空间向量的坐标的概念可知p=(2,-1,3),q=(-1,2,0),r=(1,3,-1),s=(0,-3,0).
2.B 设向量p在基底{a+b,a-b,c}下的坐标为(x,y,z),则p=a+2b+3c=x(a+b)+y(a-b)+zc=(x+y)a+(x-y)b+zc,所以解得故p在基底{a+b,a-b,c}下的坐标为.
3.C 因为向量a=(2,0,-1),所以2a=(4,0,-2),又向量b=(0,1,-2),所以2a-b=(4,0,-2)-(0,1,-2)=(4,-1,0).故选C.
4.B 由题意可知,a·b=3x+2(2-x)<0,解得x<-4,易知a,b不共线,故选B.
5.答案 -2
解析 易得c-a=(0,0,-1),2b=(2,4,2),∴(c-a)·2b=0+0-2=-2.
6.答案 2
解析 因为a,b,c为共面向量,所以存在唯一的实数对(λ,μ),使得c=λa+μb,即(2,m,-1)=λ(1,0,-1)+μ(0,2,1),所以解得
7.D 由题意得=(-6,1,2k),=(-3,2,-k).
∵∠C=90°,∴⊥,∴·=-6×(-3)+1×2+2k×(-k)=-2k2+20=0,∴k=±.故选D.
8.C ∵C为线段AB上一点,且=,∴=,设C(x,y,z),则(x-4,y-1,z-3)=(-2,-6,-2)=,
∴解得∴C.故选C.
9.解析 (1)根据题意,得a=(1,1,0),b=(-1,0,2),则ka+b=(k-1,k,2),ka-2b=(k+2,k,-4).
若向量ka+b,ka-2b互相垂直,则(ka+b)·(ka-2b)=(k-1,k,2)·(k+2,k,-4)=(k-1)(k+2)+k2-8=0,∴2k2+k-10=0,解得k=-或k=2.
(2)由(1)知,a=(1,1,0),b=(-1,0,2),则λa-b=(λ+1,λ,-2),a-λb=(1+λ,1,-2λ).
由向量λa-b,a-λb共线,可设λa-b=μ(a-λb),μ∈R,则解得λ=μ=±1.
10.D 由题意得=(-2,-1,3),=(1,-3,2).
因为向量a分别与向量,垂直,
所以即
解得故a=(-1,-1,-1),
因此|a|==.故选D.
11.B ∵A(-2,0,8),P(m,m,m),B(4,-4,6),
∴=(-2-m,-m,8-m),=(4-m,-4-m,6-m),
由题意得cos 60°=
=,
∴m2-4m+4=0,∴m=2.
12.答案
解析 由题意得a·b=-9+0+20=11,|a|=5,所以向量b在向量a上的投影数量为=.
13.解析 (1)由题意得D(1,2,1),∴=(1,1,-1),∴||==.
(2)易知=(1,-2,1),∴·=2-2a+1=1,解得a=1,∴=(2,1,1),
∴cos<,>===,
即向量与夹角的余弦值为.
14.A 由题意得M(2,1,-2),∴点M关于平面yOz对称的点的坐标为(-2,1,-2).故选A.
15.A ∵M(-1,0,2),N(3,2,-4),∴线段MN的中点Q的坐标为(1,1,-1),∴点Q与坐标原点O之间的距离|QO|==.故选A.
16.答案
解析 由题意知,A(a,0,0),B(0,b,0),C(0,0,c).由重心坐标公式得点G的坐标为.
17.解析 (1)设正三棱柱的侧棱长为h.
由题意得A(0,-1,0),B(,0,0),C(0,1,0),B1(,0,h),C1(0,1,h),则=(,1,h),=(-,1,h).因为AB1⊥BC1,所以·=-3+1+h2=0,解得h=(负值舍去).故正三棱柱的侧棱长为.
(2)由(1)可知=(,1,),=(-,1,0),
所以·=-3+1=-2,||=,||=2,
所以cos<,>==-.
能力提升练
1.A 2.D 3.C 7.C 8.B 9.A 10.A 11.BD
12.B
1.A 因为a∥b,所以==,解得x=2,y=-4,所以a=(2,4,1),b=(-2,-4,-1).
因为b⊥c,所以b·c=0,即-6+8-z=0,解得z=2,所以c=(3,-2,2),
所以a+c=(5,2,3),b+c=(1,-6,1),
所以(a+c)·(b+c)=5-12+3=-4,|a+c|==,|b+c|==.
设a+c与b+c的夹角为θ,则cos
2.D 易得B(,,0),设C(x,y,z),则=(x,y,z),=(x-,y-,z),=(-2,2,0),
由cos<,>=
==,
整理可得x-y=-①.
由||=||=3,得=,化简得x+y=②.
联立①②,解得x=,y=,则·=·(0,2,0)=3.
故选D.
3.C ∵点Q在直线OP上运动,∴O,P,Q三点共线,∴存在唯一的实数λ,使得=λ=(λ,λ,2λ),
∴=(1-λ,2-λ,3-2λ),=(2-λ,1-λ,2-2λ),
∴·=(1-λ)(2-λ)+(2-λ)(1-λ)+(3-2λ)·(2-2λ)=6λ2-16λ+10=6-,
当且仅当λ=时,上式取得最小值,
此时点Q的坐标为.故选C.
4.答案
解析 易得a+kb=(1-k,1,2k),2a+b=(1,2,2).
由题意得(a+kb)·(2a+b)>0且a+kb,2a+b不共线,
∴1-k+2+4k>0,且==不成立,解得k>-1且k≠,∴实数k的取值范围为.
5.答案
解析 由题意可得⊥,⊥,⊥.
利用向量数量积的运算公式,可得解得∴x+y=-=.
6.解析 (1)根据题意,得=(1,-3,2),由点D在直线AC上,可设=λ=λ(1,-3,2),λ∈R.
设O为坐标原点,则=+=(0,2,3)+λ(1,-3,2)=(λ,2-3λ,3+2λ),=-=(λ,2-3λ,3+2λ)-(-2,1,6)=(λ+2,1-3λ,2λ-3),
故·=(1,-3,2)·(λ+2,1-3λ,2λ-3)=λ+2-3+9λ+4λ-6=14λ-7=0,∴λ=,
∴=,∴D.
(2)根据题意,得=(2,1,-3),=(3,-2,-1),
∴||==,||==,
·=2×3+1×(-2)+(-3)×(-1)=7,
∴cos B=cos<,>===,∴sin B=,
∴平行四边形的面积为××=7,
故以BA,BC为邻边的平行四边形的面积为7.
7.C 如图,以AB,AC,AA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系Axyz,
则A1(0,0,1),B1(1,0,1),∴=(1,0,0),∴=(λ,0,0),则P(λ,0,1),又N,B(1,0,0),M,所以=,=,所以·=λ-+-=0,解得λ=.故选C.
8.B 取AC的中点O,连接OP,OB.
∵PA=PC,∴AC⊥OP.
∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,
∴OP⊥平面ABC.
∵AB=BC,
∴AC⊥OB.
以O为坐标原点,建立如图所示的空间直角坐标系,
∵△PAC是等腰直角三角形,PA=PC=4,△ABC为等边三角形,
∴A(2,0,0),C(-2,0,0),P(0,0,2),D(,,0),
∴=(-4,0,0),=(,,-2),
∴cos<,>===-.故选B.
9.A 如图,设D在底面半圆上的射影为D1,连接AD1,交BC于点O,连接A1D,交B1C1于点O1.
依题意知AD1⊥BC,A1D⊥B1C1,O,O1分别是下底面、上底面半圆的圆心.连接OO1,则OO1与上、下底面垂直,所以OO1⊥OB,OO1⊥OA.
以OB,OA,OO1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.设几何体的高为h(h>0),则B(2,0,0),D(0,-2,h),A(0,2,0),B1(2,0,h),所以=(-2,-2,h),=(2,-2,h).
所以cos<,>===,即=,所以h=4(负值舍去).所以几何体的体积为×π×22×4+×4×2×4=16+8π.故选A.
10.A 建立如图所示的空间直角坐标系Axyz,
则G,E,设D(0,y,0),F(x,0,0),其中x,y∈(0,1),则=,=,
∵⊥,∴·=0,即-x-y+=0,即x+2y=1,又∵0
∴当y=时,||min==;当y=0时,||=1;当y=时,||=,故的模的取值范围为.
11.BD ∵点P在侧面BCC1B1上运动,平面BCC1B1∥平面AA1D1D,∴点P到平面AA1D1D的距离即为点C到平面AA1D1D的距离,即为正方体的棱长,∴=·CD=××1×1×1=,故A中结论错误.
以D为坐标原点,建立如图所示的空间直角坐标系,
则A(1,0,0),B(1,1,0),D1(0,0,1),B1(1,1,1),C(0,1,0),∴=(-1,-1,1),=(-1,0,-1),设P(x,1,z)(0≤x≤1,0≤z≤1),则=(x-1,1,z).
∵AP⊥BD1,∴·=1-x-1+z=0,∴x=z,
∴P(x,1,x),∴=(x,0,x),∴=-x,即B1,P,C三点共线,∴点P必在线段B1C上,故B中结论正确.
易知C1(0,1,1),∴=(-1,0,1),又=(x-1,1,x),∴·=1-x+x=1,∴AP与BC1不垂直,故C中结论错误.
易知A1(1,0,1),D(0,0,0),∴=(-1,1,0),=(1,0,1),又=(x-1,1,x),∴=x+(其中0≤x≤1),∴,,共面,又AP 平面A1C1D,∴AP∥平面A1C1D,故D中结论正确.
故选BD.
12.B 建立如图所示的空间直角坐标系Axyz,
则D1(0,1,),C(1,1,0).
∵E为线段AB上的一个动点,
∴设E(t,0,0)(0≤t≤1),
则|D1E|==,|CE|=,
故问题转化为求y=+(0≤t≤1)的最小值,即转化为求平面直角坐标系tOy中的一个动点P(t,0)到两定点M(0,-2),N(1,1)的距离之和的最小值问题,如图所示:
由此可知,当M,P,N三点共线时,
=|MN|==,故=.
故选B.
13.解析 (1)由PB=2AP得P,
所以M,所以|PM|=
=.
(2)由题意得P.设点Q(a,1,a),a∈[0,1],则|PQ|===,所以当a=时,|PQ|取得最小值,此时点Q的坐标为.
