4.3公式法(第1课时)同步课件(共24张PPT)
文档属性
| 名称 | 4.3公式法(第1课时)同步课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:47 | ||
图片预览






文档简介
(共24张PPT)
4.3 公式法
(第一课时)
素养目标
技能目标
知识目标
使学生了解运用公式法因式分解的意义。使学生掌握用平方差公式因式分解。
使学生了解因式分解时,首先考虑用提公因式法的方法,再考虑用平方差公式的方法。
通过学方差公式因式分解,再引导学生利用乘法公式的过程中,培养学生逆向思维的意识,同时让学生了解换元的思想方法。
教学重点
教学难点
让学生掌握用平方差公式因式分解。
将一些单项式化为平方形式,再用平方差公式因式分解,培养学生多步骤因式分解的能力。
思考1:
提公因式法的概念
如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的方法叫做提公因式法.
做一做
把下列各式分解因式.
(1)4xy2-2xy
(2)a2b-5ab+9b
(3)-3ma3+6ma2-12ma
2xy(4y-1)
b(a2 – 5a+9)
-3ma(a2 – 2a+4)
思考2:
如果一个多项式的各项不具备相同的因式,是否就不能因式分解了呢??
例如:x2-4 9a2-b2
思考3:
多项式a2-b2有什么特点?你能将它分解因式吗?
是a,b两数的平方差的形式。
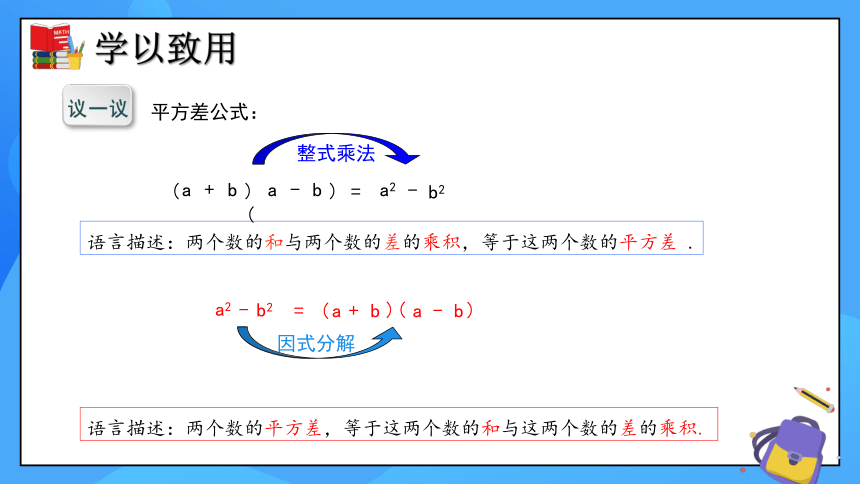
议一议
平方差公式:
)
)(
(
b
a
b
a
-
+
=
b2
a2
-
)
)(
(
b
a
b
a
b2
a2
-
+
=
-
整式乘法
因式分解
语言描述:两个数的和与两个数的差的乘积,等于这两个数的平方差 .
语言描述:两个数的平方差,等于这两个数的和与这两个数的差的乘积.
例1.
下列多项式能转化成( )2-( )2的形式吗?如果能,请将其转化成( )2-( )2的形式。
(1) m2 -81
(2) 1 -16b2
(3) 4m2+9
(4) a2x2 -25y 2
(5) -x2 -25y2
= m2 - 92
= 12-(4b)2
不能转化为平方差形式
=(ax)2 -(5y)2
不能转化为平方差形式
= [3(m+n)]2 – (m–n)2
(5) 9(m+n)2 – (m-n)2
a2 - b2 = (a+b)(a-b)
运用平方差公式因式分解,应注意:
①公式右边是两个二项式的积,且这两个二项式有一项完全相同(即a),另一项互为相反数(即b和-b).
②公式左边是这两项的平方差.
③公式中的字母即可表示单项式也可以表示多项式.
例2.
将下列各式分解因式:
a
a
b
b
(
+
)
(
-
)
a2 - b2 =
解:原式=
(2x)2
- 32
= ( 2x +
(2x -
3)
3)
(1) 4x2-9
例2.
将下列各式分解因式:
a
a
b
b
(
+
)
(
-
)
a2 - b2 =
(2) (x+m)2-(x+n)2
=[ (x+m) + (x+n) ] · [ (x+m) - (x+n) ]
=(2x+m+n)(m-n)
(2) (x+m)2 - (x+n)2
方法总结:
公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解.
利用平方差公式分解两项式的一般步骤:
1. 找出公式中的a、b;
2. 转化成a2-b2的形式;
3. 根据公式a2-b2=(a+b) (a-b) 写出结果.
例3.
将下列各式分解因式:
解:
(1)x4-y4
原式=(x2)2-(y2)2
=(x2+y2)(x2-y2)
=(x2+y2)(x+y)(x-y)
分解因式后,一定要检查是否还有能继续分解的因式,若有,则需继续分解.
例3.
将下列各式分解因式:
(2)2x3 – 8x.
解:原式= 2x(x2-4)
= 2x(x2-22)
= 2x(x+2)(x-2).
当多项式的各项含有公因式时,通常先提出这个公因式,然后再进一步因式分解.
例3.
将下列各式分解因式:
公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解。
解:原式 =(a + b)2 – [3(a - b) ]2
= [ (a + b) + 3(a - b)][ (a + b) - 3(a - b)]
= (a + b + 3a - 3b)(a + b - 3a + 3b)
= (4a - 2b)(4b - 2a)
= 4(2a - b)(2b - a);
(3)(a + b)2 - 9(a - b)2
方法总结:
分解因式前应先分析多项式的特点,一般先提公因式,再套用公式.注意分解因式必须进行到每一个多项式都不能再分解因式为止.
做一做
1.判断正误:
a2和b2的符号相反
(1)x2+y2=(x+y)(x+y); ( )
(2)x2-y2=(x+y)(x-y); ( )
(3)-x2+y2=(-x+y)(-x-y); ( )
(4)-x2-y2=-(x+y)(x-y); ( )
做一做
2.如图,大小两圆的圆心相同,已知它们的半径分别是R cm和r cm,求它们所围成的环形的面积。如果R=8.45cm,r=3.45cm呢?( =3.14)
解: R2- r2
= (R2-r2)
= (R+r)(R-r)
当R=8.45,r=3.45时,
原式=(8.45+3.45) ×(8.45-3.45) ×3.14
=186.83 cm2
做一做
3.求证:当n为整数时,多项式(2n+1)2-(2n-1)2一定能被8整除.
即多项式(2n+1)2-(2n-1)2一定能被8整除.
证明:原式=(2n+1+2n-1)(2n+1-2n+1)=4n 2=8n,
∵n为整数,
∴8n被8整除,
解决整除的基本思路就是将代数式化为整式乘积的形式,然后分析能被哪些数或式子整除.
思想方法
逆向思维,转化思维,整体思想。
公式法
平方差公式:a2-b2=(a+b)(a-b)
平方差公式中的a与b既可以是单项式,又可以是多项式;
步骤:
一提:公因式;
二套:公式;
三查:多项式的因式分解有没有分解到不能再分解为止.
1.已知4m+n=40,2m-3n=5.求(m+2n)2-(3m-n)2的值.
原式=-40×5=-200.
解:原式=[(m+2n)+(3m-n)][(m+2n)-(3m+n)]
=(4m+n)(3n-2m)
=-(4m+n)(2m-3n),
当4m+n=40,2m-3n=5时,
习题4.4第1、2题
4.3 公式法
(第一课时)
素养目标
技能目标
知识目标
使学生了解运用公式法因式分解的意义。使学生掌握用平方差公式因式分解。
使学生了解因式分解时,首先考虑用提公因式法的方法,再考虑用平方差公式的方法。
通过学方差公式因式分解,再引导学生利用乘法公式的过程中,培养学生逆向思维的意识,同时让学生了解换元的思想方法。
教学重点
教学难点
让学生掌握用平方差公式因式分解。
将一些单项式化为平方形式,再用平方差公式因式分解,培养学生多步骤因式分解的能力。
思考1:
提公因式法的概念
如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的方法叫做提公因式法.
做一做
把下列各式分解因式.
(1)4xy2-2xy
(2)a2b-5ab+9b
(3)-3ma3+6ma2-12ma
2xy(4y-1)
b(a2 – 5a+9)
-3ma(a2 – 2a+4)
思考2:
如果一个多项式的各项不具备相同的因式,是否就不能因式分解了呢??
例如:x2-4 9a2-b2
思考3:
多项式a2-b2有什么特点?你能将它分解因式吗?
是a,b两数的平方差的形式。
议一议
平方差公式:
)
)(
(
b
a
b
a
-
+
=
b2
a2
-
)
)(
(
b
a
b
a
b2
a2
-
+
=
-
整式乘法
因式分解
语言描述:两个数的和与两个数的差的乘积,等于这两个数的平方差 .
语言描述:两个数的平方差,等于这两个数的和与这两个数的差的乘积.
例1.
下列多项式能转化成( )2-( )2的形式吗?如果能,请将其转化成( )2-( )2的形式。
(1) m2 -81
(2) 1 -16b2
(3) 4m2+9
(4) a2x2 -25y 2
(5) -x2 -25y2
= m2 - 92
= 12-(4b)2
不能转化为平方差形式
=(ax)2 -(5y)2
不能转化为平方差形式
= [3(m+n)]2 – (m–n)2
(5) 9(m+n)2 – (m-n)2
a2 - b2 = (a+b)(a-b)
运用平方差公式因式分解,应注意:
①公式右边是两个二项式的积,且这两个二项式有一项完全相同(即a),另一项互为相反数(即b和-b).
②公式左边是这两项的平方差.
③公式中的字母即可表示单项式也可以表示多项式.
例2.
将下列各式分解因式:
a
a
b
b
(
+
)
(
-
)
a2 - b2 =
解:原式=
(2x)2
- 32
= ( 2x +
(2x -
3)
3)
(1) 4x2-9
例2.
将下列各式分解因式:
a
a
b
b
(
+
)
(
-
)
a2 - b2 =
(2) (x+m)2-(x+n)2
=[ (x+m) + (x+n) ] · [ (x+m) - (x+n) ]
=(2x+m+n)(m-n)
(2) (x+m)2 - (x+n)2
方法总结:
公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解.
利用平方差公式分解两项式的一般步骤:
1. 找出公式中的a、b;
2. 转化成a2-b2的形式;
3. 根据公式a2-b2=(a+b) (a-b) 写出结果.
例3.
将下列各式分解因式:
解:
(1)x4-y4
原式=(x2)2-(y2)2
=(x2+y2)(x2-y2)
=(x2+y2)(x+y)(x-y)
分解因式后,一定要检查是否还有能继续分解的因式,若有,则需继续分解.
例3.
将下列各式分解因式:
(2)2x3 – 8x.
解:原式= 2x(x2-4)
= 2x(x2-22)
= 2x(x+2)(x-2).
当多项式的各项含有公因式时,通常先提出这个公因式,然后再进一步因式分解.
例3.
将下列各式分解因式:
公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解。
解:原式 =(a + b)2 – [3(a - b) ]2
= [ (a + b) + 3(a - b)][ (a + b) - 3(a - b)]
= (a + b + 3a - 3b)(a + b - 3a + 3b)
= (4a - 2b)(4b - 2a)
= 4(2a - b)(2b - a);
(3)(a + b)2 - 9(a - b)2
方法总结:
分解因式前应先分析多项式的特点,一般先提公因式,再套用公式.注意分解因式必须进行到每一个多项式都不能再分解因式为止.
做一做
1.判断正误:
a2和b2的符号相反
(1)x2+y2=(x+y)(x+y); ( )
(2)x2-y2=(x+y)(x-y); ( )
(3)-x2+y2=(-x+y)(-x-y); ( )
(4)-x2-y2=-(x+y)(x-y); ( )
做一做
2.如图,大小两圆的圆心相同,已知它们的半径分别是R cm和r cm,求它们所围成的环形的面积。如果R=8.45cm,r=3.45cm呢?( =3.14)
解: R2- r2
= (R2-r2)
= (R+r)(R-r)
当R=8.45,r=3.45时,
原式=(8.45+3.45) ×(8.45-3.45) ×3.14
=186.83 cm2
做一做
3.求证:当n为整数时,多项式(2n+1)2-(2n-1)2一定能被8整除.
即多项式(2n+1)2-(2n-1)2一定能被8整除.
证明:原式=(2n+1+2n-1)(2n+1-2n+1)=4n 2=8n,
∵n为整数,
∴8n被8整除,
解决整除的基本思路就是将代数式化为整式乘积的形式,然后分析能被哪些数或式子整除.
思想方法
逆向思维,转化思维,整体思想。
公式法
平方差公式:a2-b2=(a+b)(a-b)
平方差公式中的a与b既可以是单项式,又可以是多项式;
步骤:
一提:公因式;
二套:公式;
三查:多项式的因式分解有没有分解到不能再分解为止.
1.已知4m+n=40,2m-3n=5.求(m+2n)2-(3m-n)2的值.
原式=-40×5=-200.
解:原式=[(m+2n)+(3m-n)][(m+2n)-(3m+n)]
=(4m+n)(3n-2m)
=-(4m+n)(2m-3n),
当4m+n=40,2m-3n=5时,
习题4.4第1、2题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
