5.3 分式的加减法(第2课时)课件(共22张PPT)
文档属性
| 名称 | 5.3 分式的加减法(第2课时)课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:47 | ||
图片预览






文档简介
(共22张PPT)
5.3 分式的加减法
(第二课时)
素养目标
技能目标
知识目标
理解并掌握异分母分式的加减法法则。并会运用它熟练地进行异分母分式的加减运算。
通过类比的方法,经历探索异分母分式加减法运算法则的过程,理解其算理,培养学生代数化归的数学能力及有条理地表达的能力。
在活动中培养学生善于发现、归纳的学习习惯。培养学生学以致用的意识和能力。
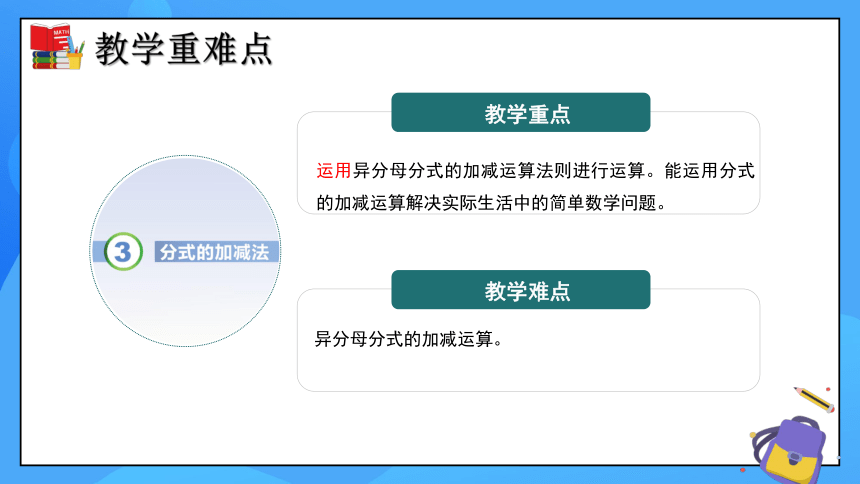
教学重点
教学难点
运用异分母分式的加减运算法则进行运算。能运用分式的加减运算解决实际生活中的简单数学问题。
异分母分式的加减运算。
思考1:
异分母分数的加减法则是什么吗?
异分母分数相加减,先通分,化为同分母分数后,再加减.
请计算 ( ), ( ).
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数相加减
异分母分数相加减,先通分,
变为同分母的分数,再加减 .
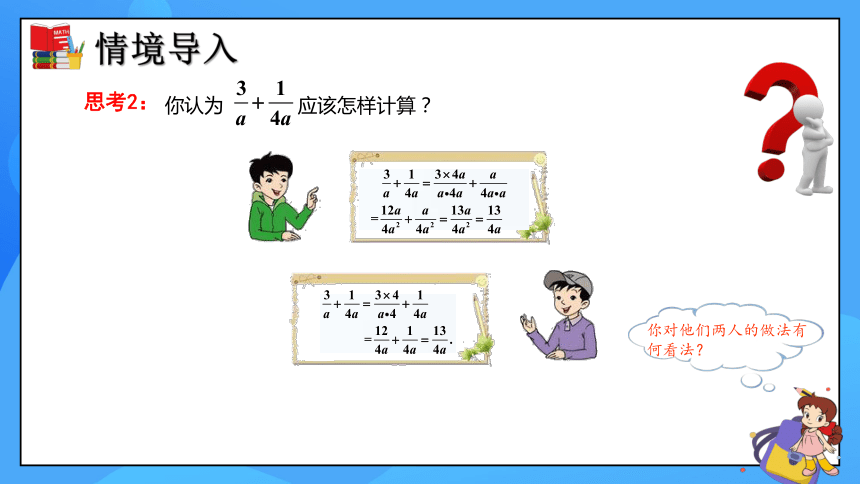
思考2:
你认为 应该怎样计算?
你对他们两人的做法有何看法?
根据分式的基本性质,异分母的分式可以化为同分母的分式,这一过程称为分式的通分.
异分母分式通分时,为了方便计算,通常取最简单的公分母(简称最简公分母)作为它们的共同分母.
异分母分式的加减法则:
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
上述法则用式子表示为:
类比同分母分数的加减法法则,你能说出同分母分式的加减法则吗?
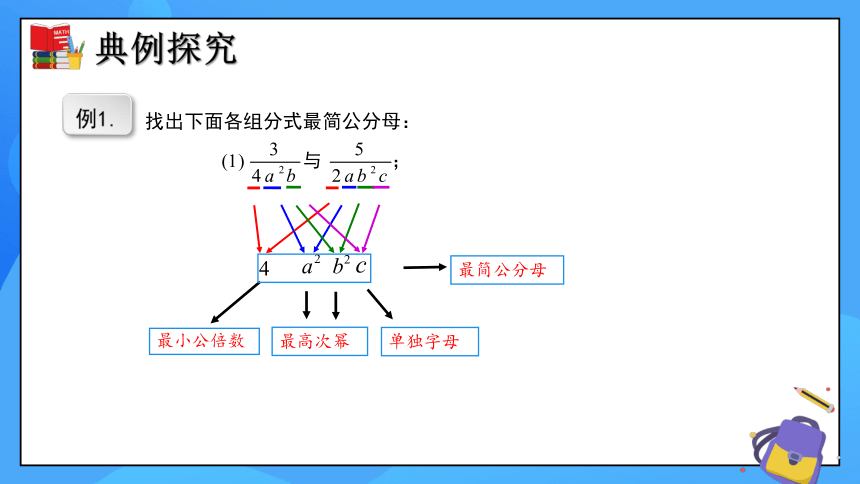
例1.
找出下面各组分式最简公分母:
最小公倍数
最简公分母
最高次幂
单独字母
例1.
找出下面各组分式最简公分母:
注意:最简公分母的系数,取各个分母的系数的最小公倍数,字母及式子取各分母中所有分母和式子的最高次幂.
不同的因式
分解因式
找最简公分母:
x(x-5)(x+5)
(x+y)2 (x-y)
例2.
计算下列式子:
(1)
解: (1)
例2.
计算下列式子:
(2)
解:(2)
例2.
计算下列式子:
(3)
解:(3)
例3.
小刚家和小丽家到学校的路程都是 3 km,其中小丽走的是平路,骑车速度是 2v km/h.小刚需要走 1 km的上坡路、 2 km的下坡路,在上坡路上的骑车速度为 v km/h,在下坡路上的骑车速度为 3v km/h.那么
(1)小刚从家到学校需要多长时间?
(2)小刚和小丽谁在路上花费的时间少?少用多长时间?
解(1)小刚从家到学校需要
(2)小丽从家到学校需要
因为
所以小丽在路上花费的时间少
小丽比小刚在路上花费时间少
的运算结果是( )
A. B. C. D.
C
因式分解
先化简,再确定最简公分母
通分
整式加减法则
最简分式
2.
解:原式
分子是多项式时要加括号再相加减
思想方法
转化思想,类比思想,特殊到一般,整体思想。
加减法运算法则
异分母加减法则:异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
注意事项:
1.通分的关键就是找最简公分母,对于分母是多项式且能够进行分解因式的要先分解后再类比最小公倍数找最简公分母。
2.通分前是单项式的分子通分后就可能是多项式了,运算时要添括号。
3.运算结果要约分,有一些运算律仍然适用。
C
1.三个分式
的最简公分母是( )
B.
C.
D.
A.
4xy
3y2
12xy2
12x2y2
2. 用两种方法计算:
解:法一(按运算顺序)
原式
法二(利用乘法分配律)
原式
习题5.5第1、2题
5.3 分式的加减法
(第二课时)
素养目标
技能目标
知识目标
理解并掌握异分母分式的加减法法则。并会运用它熟练地进行异分母分式的加减运算。
通过类比的方法,经历探索异分母分式加减法运算法则的过程,理解其算理,培养学生代数化归的数学能力及有条理地表达的能力。
在活动中培养学生善于发现、归纳的学习习惯。培养学生学以致用的意识和能力。
教学重点
教学难点
运用异分母分式的加减运算法则进行运算。能运用分式的加减运算解决实际生活中的简单数学问题。
异分母分式的加减运算。
思考1:
异分母分数的加减法则是什么吗?
异分母分数相加减,先通分,化为同分母分数后,再加减.
请计算 ( ), ( ).
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数相加减
异分母分数相加减,先通分,
变为同分母的分数,再加减 .
思考2:
你认为 应该怎样计算?
你对他们两人的做法有何看法?
根据分式的基本性质,异分母的分式可以化为同分母的分式,这一过程称为分式的通分.
异分母分式通分时,为了方便计算,通常取最简单的公分母(简称最简公分母)作为它们的共同分母.
异分母分式的加减法则:
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
上述法则用式子表示为:
类比同分母分数的加减法法则,你能说出同分母分式的加减法则吗?
例1.
找出下面各组分式最简公分母:
最小公倍数
最简公分母
最高次幂
单独字母
例1.
找出下面各组分式最简公分母:
注意:最简公分母的系数,取各个分母的系数的最小公倍数,字母及式子取各分母中所有分母和式子的最高次幂.
不同的因式
分解因式
找最简公分母:
x(x-5)(x+5)
(x+y)2 (x-y)
例2.
计算下列式子:
(1)
解: (1)
例2.
计算下列式子:
(2)
解:(2)
例2.
计算下列式子:
(3)
解:(3)
例3.
小刚家和小丽家到学校的路程都是 3 km,其中小丽走的是平路,骑车速度是 2v km/h.小刚需要走 1 km的上坡路、 2 km的下坡路,在上坡路上的骑车速度为 v km/h,在下坡路上的骑车速度为 3v km/h.那么
(1)小刚从家到学校需要多长时间?
(2)小刚和小丽谁在路上花费的时间少?少用多长时间?
解(1)小刚从家到学校需要
(2)小丽从家到学校需要
因为
所以小丽在路上花费的时间少
小丽比小刚在路上花费时间少
的运算结果是( )
A. B. C. D.
C
因式分解
先化简,再确定最简公分母
通分
整式加减法则
最简分式
2.
解:原式
分子是多项式时要加括号再相加减
思想方法
转化思想,类比思想,特殊到一般,整体思想。
加减法运算法则
异分母加减法则:异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
注意事项:
1.通分的关键就是找最简公分母,对于分母是多项式且能够进行分解因式的要先分解后再类比最小公倍数找最简公分母。
2.通分前是单项式的分子通分后就可能是多项式了,运算时要添括号。
3.运算结果要约分,有一些运算律仍然适用。
C
1.三个分式
的最简公分母是( )
B.
C.
D.
A.
4xy
3y2
12xy2
12x2y2
2. 用两种方法计算:
解:法一(按运算顺序)
原式
法二(利用乘法分配律)
原式
习题5.5第1、2题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
