2023-2024学年北师大版九年级数学上册第六章 反比例函数 课件(共42张PPT)
文档属性
| 名称 | 2023-2024学年北师大版九年级数学上册第六章 反比例函数 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-06 08:28:25 | ||
图片预览










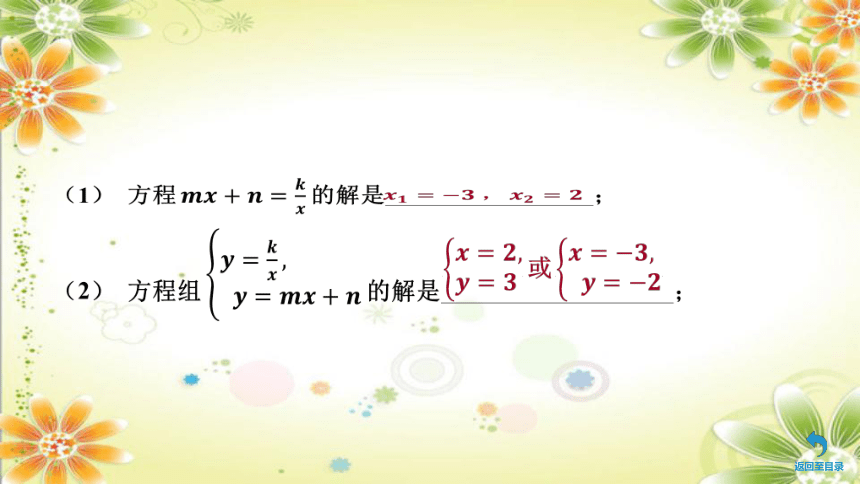

文档简介
(共42张PPT)
第六章 反比例函数
类型一 反比例函数的建模与图象的识别
例1 为了更好地保护水资源,造福人类,某工厂计划建一个容积
一定的污水处理池,池的底面积 与其深度 满足关系
式: ,则 关于 的函数图象大致是( )
A.&1& B.&2& C.&3& D.&4&
知识巩固
【点拨】借助底面积与深度之间的关系构建函数关系,并结合深度的实际意义确定图象的位置.
[答案] C
方法归纳
函数图象的辨别,关键是列出函数表达式或根据实际问题情境中所描述的两个变量之间的变化趋势来分析,同时要注意自变量的取值范围对函数图象的影响.
类型二 反比例函数的图象和性质
例2 已知反比例函数 ( 为常数).
(1) 若函数图象在第二、四象限,求 的取值范围.
(2) 当 时, 随 的增大而减小,求 的取值范围.
(3) 在图象上取一点 ,分别向 轴、 轴作垂线段,垂足分别为
, ,坐标原点为 .若四边形 的面积为6,求 的值.
【点拨】根据反比例函数 的图象的位置或性质列出关于
的不等式,求出 的取值范围;结合反比例函数 的几何意义可求解
的值.
(1) 若函数图象在第二、四象限,求 的取值范围.
【解】 反比例函数 的图象在第二、四象限,
.解得 .
的取值范围是 .
(2) 当 时, 随 的增大而减小,求 的取值范围.
[答案] 当 时, 随 的增大而减小,
.
解得 .
的取值范围是 .
(3) 在图象上取一点 ,分别向 轴、 轴作垂线段,垂足分别为
, ,坐标原点为 .若四边形 的面积为6,求 的值.
[答案] 若四边形 的面积为6,根据反比例函数 的几何意义可知 ,解得 或 .
方法归纳
结合反比例函数图象的位置或函数增减性可以确定字母系数的取值范围.求反比例函数表达式,一可借助待定系数法,二可借助反比例函数 的几何意义(图形面积保持不变).这里体现了数形结合的思想,做此类题一定要正确理解 的几何意义.
类型三 从函数图象看方程(组)、不等式的解
例3 已知反比例函数 和一次函数 的图象相交于点
, .
(1) 方程 的解是________;
(2) 方程组 的解是________;
(3) 直接写出当 时 的取值范围.
【点拨】(1)(2)中有关求方程(组)的解的问题,常化归为求一次函数与反比例函数图象交点的问题,即交点的横坐标(横、纵坐标)是对应方程(组)的解;(3)画出两个函数图象,再结合图象求得反比例函数图象在一次函数图象下方时 的取值范围即可.
(1) 方程 的解是_________________;
(2) 方程组 的解是___________________;
(3) 直接写出当 时 的取值范围.
【解】画一次函数和反比例函数的大致图象如下:
由图象可知,当 或 时,反比例函数图象在一次函数
图象的下方.
当 时, 的取值范围是 或 .
方法归纳
有关反比例函数与一次函数的交点问题,主要有两种:已知两个函数的表达式,求交点——只要联立表达式为方程组,方程组的解就是交点坐标;已知交点坐标,求表达式——把交点坐标代入含字母的表达式,求出字母的值即可确定表达式.比较两个函数值的大小,关键是利用函数图象找到交点的坐标,进而根据“同一个区域内,图象在上方的对应的函数值大”直接判断,体现了数形结合的思想.
类型四 反比例函数在实际问题中的应用
例4 某种商品上市之初做了大量的广告宣传,
其日销售量 与上市的天数 之间成正比例
函数关系;广告停止后,日销售量 与上市
的天数 之间成反比例函数关系(如图所
示).已知上市20天时,日销售量为200件.
(1) 写出该商品上市以后日销售量 (件)与上市的天数 (天)之
间的关系式.
(2) 当上市的天数为多少时,日销售量为100件?
【点拨】(1)先设出相应的函数关系式,再将已知点的坐标代入即可得出函数关系式;
(2)直接利用函数表达式可分别得出答案.
(1) 写出该商品上市以后日销售量 (件)
与上市的天数 (天)之间的关系式.
【解】当 时,设 .
把 代入,得 .
.
当 时,设 .
把 代入,得 .
.
(2) 当上市的天数为多少时,日销售量为100件?
[答案] 当 时, ,
解得 .
当 时, ,
解得 .
故当上市的天数为10天或40天时,日销售量
为100件.
方法归纳
此题是反比例函数在实际问题中的应用题,它包含两个时段的函数关系,因此在求两个函数关系式时要特别注意转折点(即公共点),它是自变量的取值范围的分界点.解决函数情境应用题的核心是通过观察,分析图象、图表、情境,捕捉有效信息,并对已获得的信息进行加工、处理和整理,分清变量之间的关系,将实际问题转化为相应的数学问题来解决.
易错示例 函数 与 在同一直角坐标系中的图象
可能是( )
A
A.&5& B.&6& C.&7& D.&8&
【错解】B,C或D
【错因分析】没有根据一次函数和反比例函数的图象与系数的关系,
对字母 分类讨论逐个判断从而出错.
1.下列四个点中,在反比例函数 的图象上的是( )
A
A. B. C. D.
课堂练习
2.已知矩形的面积为 ,相邻两边的长分别为 和 ,
则 与 之间的函数图象大致是( )
A
A.&9& B.&10& C.&11& D.&12&
(第3题图)
3.在同一平面直角坐标系中,反比例函数 和一
次函数 的图象如图,下列结论中不正确
的是( )
C
A. 的值随 值的增大而增大
B.点 的坐标为
C.
D.当 时,
(第4题图)
4.如图,已知点 是反比例函数 图象上
的一点, 轴于点 ,且 的面积为3,则
的值为___.
6
5.若正比例函数 图象与反比例函数 图象的一个交点坐标
为 ,则另一个交点的坐标为_ _______.
6.已知反比例函数 和一次函数 .
(1) 若一次函数与反比例函数的图象相交于点 ,求 和 的
值.
(2) 当 满足什么条件时,两函数的图象没有交点?
(1) 若一次函数与反比例函数的图象相交于点 ,求 和 的
值.
解:把 代入 ,
得 , .
.
(2) 当 满足什么条件时,两函数的图象没有交点?
[答案] 由题意得 ,
两函数的图象没有交点,
.解得 .
7.如图,已知曲线 ,
,点 为曲线
上的一点,且 轴于
点 , 轴于点 , , 分别
交曲线 于 , 两点,则
的面积为_ _.
8.电灭蚊器的电阻 随温度 变化的大
致图象如图所示,通电后温度由室温 上
升到 时,电阻与温度成反比例函数关系,
且在温度达到 时,电阻下降到最小值,
随后电阻随温度的升高而增加,温度每上升
,电阻增加 .
(1) 当 时,求 与 之间的函数关系式.
(2) 电灭蚊器在使用过程中,温度 在什么范围内时,电阻不超过
?
(1) 当 时,求 与 之间的函
数关系式.
解:设 .
过点 ,
.
当 时, 与 的函数关系式为 .
(2) 电灭蚊器在使用过程中,温度 在什么范围内时,电阻不超过
?
[答案] ,
当 时, .
当 时,可设 .
过点 ,
.
.
故当 时, 与 的关系式为 .
当 , 时, ;
当 , 时, .
温度 的取值范围是 .
9.如图,一次函数 的图象与反比例函
数 的图象相交于 , 两点,其中点 的坐
标为 ,点 的坐标为 .
(1) 根据函数图象,直接写出满足
的 的取值范围;
(2) 求一次函数与反比例函数的表达式;
(3) 若点 在线段 上,且 ,求点 的坐标.
(1) 根据函数图象,直接写出满足 的 的取值范围;
解: 或 .
(2) 求一次函数与反比例函数的表达式;
[答案] 反比例函数 的图象过点 ,
,解得 .
反比例函数的表达式为 .
反比例函数 的图象过点 ,
.
一次函数 的图象过点 和 ,
解得
一次函数的表达式为 .
(3) 若点 在线段 上,且 ,求点 的坐标.
[答案] 点 在线段 上,
设点 的坐标为 .
和 的高相同,
,
.
过点 作 轴,过点 , 分别作
于点 , 于点 .
, ,
.
, ,
.解得 .
.
点 的坐标为 .
谢谢大家
第六章 反比例函数
类型一 反比例函数的建模与图象的识别
例1 为了更好地保护水资源,造福人类,某工厂计划建一个容积
一定的污水处理池,池的底面积 与其深度 满足关系
式: ,则 关于 的函数图象大致是( )
A.&1& B.&2& C.&3& D.&4&
知识巩固
【点拨】借助底面积与深度之间的关系构建函数关系,并结合深度的实际意义确定图象的位置.
[答案] C
方法归纳
函数图象的辨别,关键是列出函数表达式或根据实际问题情境中所描述的两个变量之间的变化趋势来分析,同时要注意自变量的取值范围对函数图象的影响.
类型二 反比例函数的图象和性质
例2 已知反比例函数 ( 为常数).
(1) 若函数图象在第二、四象限,求 的取值范围.
(2) 当 时, 随 的增大而减小,求 的取值范围.
(3) 在图象上取一点 ,分别向 轴、 轴作垂线段,垂足分别为
, ,坐标原点为 .若四边形 的面积为6,求 的值.
【点拨】根据反比例函数 的图象的位置或性质列出关于
的不等式,求出 的取值范围;结合反比例函数 的几何意义可求解
的值.
(1) 若函数图象在第二、四象限,求 的取值范围.
【解】 反比例函数 的图象在第二、四象限,
.解得 .
的取值范围是 .
(2) 当 时, 随 的增大而减小,求 的取值范围.
[答案] 当 时, 随 的增大而减小,
.
解得 .
的取值范围是 .
(3) 在图象上取一点 ,分别向 轴、 轴作垂线段,垂足分别为
, ,坐标原点为 .若四边形 的面积为6,求 的值.
[答案] 若四边形 的面积为6,根据反比例函数 的几何意义可知 ,解得 或 .
方法归纳
结合反比例函数图象的位置或函数增减性可以确定字母系数的取值范围.求反比例函数表达式,一可借助待定系数法,二可借助反比例函数 的几何意义(图形面积保持不变).这里体现了数形结合的思想,做此类题一定要正确理解 的几何意义.
类型三 从函数图象看方程(组)、不等式的解
例3 已知反比例函数 和一次函数 的图象相交于点
, .
(1) 方程 的解是________;
(2) 方程组 的解是________;
(3) 直接写出当 时 的取值范围.
【点拨】(1)(2)中有关求方程(组)的解的问题,常化归为求一次函数与反比例函数图象交点的问题,即交点的横坐标(横、纵坐标)是对应方程(组)的解;(3)画出两个函数图象,再结合图象求得反比例函数图象在一次函数图象下方时 的取值范围即可.
(1) 方程 的解是_________________;
(2) 方程组 的解是___________________;
(3) 直接写出当 时 的取值范围.
【解】画一次函数和反比例函数的大致图象如下:
由图象可知,当 或 时,反比例函数图象在一次函数
图象的下方.
当 时, 的取值范围是 或 .
方法归纳
有关反比例函数与一次函数的交点问题,主要有两种:已知两个函数的表达式,求交点——只要联立表达式为方程组,方程组的解就是交点坐标;已知交点坐标,求表达式——把交点坐标代入含字母的表达式,求出字母的值即可确定表达式.比较两个函数值的大小,关键是利用函数图象找到交点的坐标,进而根据“同一个区域内,图象在上方的对应的函数值大”直接判断,体现了数形结合的思想.
类型四 反比例函数在实际问题中的应用
例4 某种商品上市之初做了大量的广告宣传,
其日销售量 与上市的天数 之间成正比例
函数关系;广告停止后,日销售量 与上市
的天数 之间成反比例函数关系(如图所
示).已知上市20天时,日销售量为200件.
(1) 写出该商品上市以后日销售量 (件)与上市的天数 (天)之
间的关系式.
(2) 当上市的天数为多少时,日销售量为100件?
【点拨】(1)先设出相应的函数关系式,再将已知点的坐标代入即可得出函数关系式;
(2)直接利用函数表达式可分别得出答案.
(1) 写出该商品上市以后日销售量 (件)
与上市的天数 (天)之间的关系式.
【解】当 时,设 .
把 代入,得 .
.
当 时,设 .
把 代入,得 .
.
(2) 当上市的天数为多少时,日销售量为100件?
[答案] 当 时, ,
解得 .
当 时, ,
解得 .
故当上市的天数为10天或40天时,日销售量
为100件.
方法归纳
此题是反比例函数在实际问题中的应用题,它包含两个时段的函数关系,因此在求两个函数关系式时要特别注意转折点(即公共点),它是自变量的取值范围的分界点.解决函数情境应用题的核心是通过观察,分析图象、图表、情境,捕捉有效信息,并对已获得的信息进行加工、处理和整理,分清变量之间的关系,将实际问题转化为相应的数学问题来解决.
易错示例 函数 与 在同一直角坐标系中的图象
可能是( )
A
A.&5& B.&6& C.&7& D.&8&
【错解】B,C或D
【错因分析】没有根据一次函数和反比例函数的图象与系数的关系,
对字母 分类讨论逐个判断从而出错.
1.下列四个点中,在反比例函数 的图象上的是( )
A
A. B. C. D.
课堂练习
2.已知矩形的面积为 ,相邻两边的长分别为 和 ,
则 与 之间的函数图象大致是( )
A
A.&9& B.&10& C.&11& D.&12&
(第3题图)
3.在同一平面直角坐标系中,反比例函数 和一
次函数 的图象如图,下列结论中不正确
的是( )
C
A. 的值随 值的增大而增大
B.点 的坐标为
C.
D.当 时,
(第4题图)
4.如图,已知点 是反比例函数 图象上
的一点, 轴于点 ,且 的面积为3,则
的值为___.
6
5.若正比例函数 图象与反比例函数 图象的一个交点坐标
为 ,则另一个交点的坐标为_ _______.
6.已知反比例函数 和一次函数 .
(1) 若一次函数与反比例函数的图象相交于点 ,求 和 的
值.
(2) 当 满足什么条件时,两函数的图象没有交点?
(1) 若一次函数与反比例函数的图象相交于点 ,求 和 的
值.
解:把 代入 ,
得 , .
.
(2) 当 满足什么条件时,两函数的图象没有交点?
[答案] 由题意得 ,
两函数的图象没有交点,
.解得 .
7.如图,已知曲线 ,
,点 为曲线
上的一点,且 轴于
点 , 轴于点 , , 分别
交曲线 于 , 两点,则
的面积为_ _.
8.电灭蚊器的电阻 随温度 变化的大
致图象如图所示,通电后温度由室温 上
升到 时,电阻与温度成反比例函数关系,
且在温度达到 时,电阻下降到最小值,
随后电阻随温度的升高而增加,温度每上升
,电阻增加 .
(1) 当 时,求 与 之间的函数关系式.
(2) 电灭蚊器在使用过程中,温度 在什么范围内时,电阻不超过
?
(1) 当 时,求 与 之间的函
数关系式.
解:设 .
过点 ,
.
当 时, 与 的函数关系式为 .
(2) 电灭蚊器在使用过程中,温度 在什么范围内时,电阻不超过
?
[答案] ,
当 时, .
当 时,可设 .
过点 ,
.
.
故当 时, 与 的关系式为 .
当 , 时, ;
当 , 时, .
温度 的取值范围是 .
9.如图,一次函数 的图象与反比例函
数 的图象相交于 , 两点,其中点 的坐
标为 ,点 的坐标为 .
(1) 根据函数图象,直接写出满足
的 的取值范围;
(2) 求一次函数与反比例函数的表达式;
(3) 若点 在线段 上,且 ,求点 的坐标.
(1) 根据函数图象,直接写出满足 的 的取值范围;
解: 或 .
(2) 求一次函数与反比例函数的表达式;
[答案] 反比例函数 的图象过点 ,
,解得 .
反比例函数的表达式为 .
反比例函数 的图象过点 ,
.
一次函数 的图象过点 和 ,
解得
一次函数的表达式为 .
(3) 若点 在线段 上,且 ,求点 的坐标.
[答案] 点 在线段 上,
设点 的坐标为 .
和 的高相同,
,
.
过点 作 轴,过点 , 分别作
于点 , 于点 .
, ,
.
, ,
.解得 .
.
点 的坐标为 .
谢谢大家
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
