6.3菱形的性质与判定 课件

课件18张PPT。有一组邻边相等的平行四边形叫菱形． 平行四边形 邻边相等菱形在平行四边形中，如果内角大小保持不变，仅改变边的长度，请仔细观察和思考，在这变化过程中，哪些关系没变？哪些关系变了？ 如果改变了边的长度，使两邻边相等，那么这个平行四边形成为怎样的四边形？AB=BCABCD四边形ABCD是菱形观察与思考菱形欣赏菱形欣赏 特殊平行四边形6、3 菱形的性质与判定 学习目标
1、知道什么是菱形
2、理解并掌握菱形的性质和判定
3、能运用菱形的性质和判定解决简单的几何问题。1.菱形是轴对称图形，有两条对称轴它们是对角线所在的直线
2.菱形的两条对角线互相垂直。
3.菱形的四条边都相等。结 论证明：
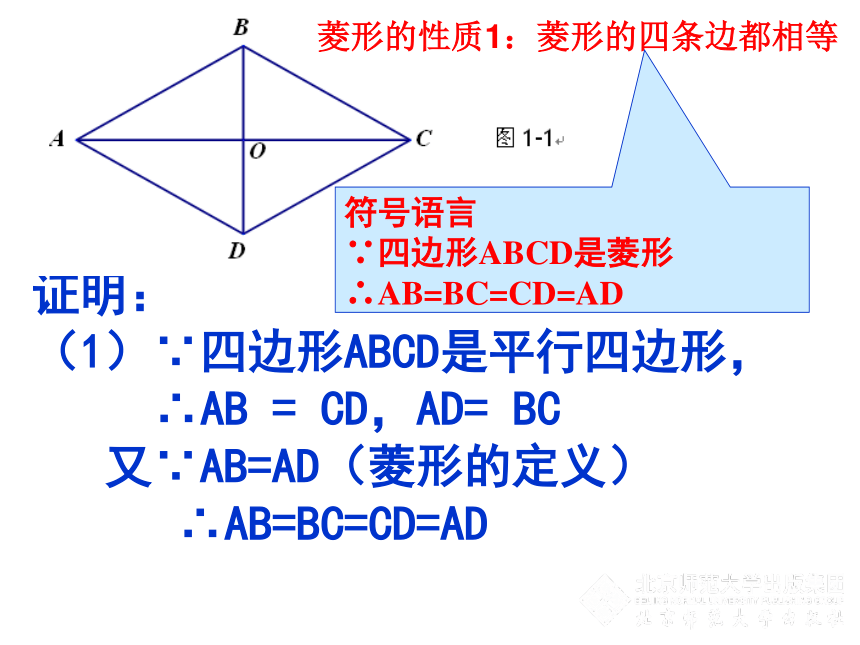
（1）∵四边形ABCD是平行四边形，
∴AB = CD，AD= BC
又∵AB=AD（菱形的定义）
∴AB=BC=CD=AD菱形的性质1：菱形的四条边都相等符号语言
∵四边形ABCD是菱形
∴AB=BC=CD=AD
菱形的性质2 ：菱形的对角线互相垂直平分（2）∵AB=AD
∴△ABD是等腰三角形
又∵四边形ABCD是平行四边形
∴OB=OD（平行四边形的对角线互相平分）
在等腰三角形ABD中，
∵OB=OD
∴AO⊥BD
即AC⊥BD
符号语言
∵四边形ABCD是菱形
∴ AC⊥BD 菱形是特殊的平行四边形，它除具有平行四边形的所有性质外，还具有平行四边形所没有的特殊性质：性质定理1. 菱形的四条边都相等。性质定理2. 菱形的两条对角线互相垂直。
学以致用
1、若菱形的边长等于5cm，那么菱形的周长为 。
2、菱形具有而一般平行四边形不具有的性质是（ ）

A.对角线相等 B.对边相等
C.对角线互相垂直 D.对角相等
20cm C1、已知:如图,四边形ABCD中，
AB=BC=CD=DA.
求证: 四边形ABCD是菱形 证明:∵AB=CD,AD=BC ∴四边形ABCD是平行四边形 又∵AB=BC ∴四边形ABCD是菱形(菱形定义)2、已知:如图,在□ABCD中,对角线AC
与BD交于点O,AC⊥BD
求证: □ABCD是菱形证明:∵四边形ABCD是平行四边形 ∴OA=OC 又∵AC⊥BD∴BD是线段AC的垂直平分线 ∴BA=BC∴四边形ABCD是菱形(菱形定义)菱形的判定定理1四条边相等的四边形是菱形 几何语言 ∵AB=BC=CD=DA∴四边形ABCD是菱形
菱形的判定定理2对角线互相垂直的平行四边形是菱形几何语言
∵四边形ABCD是平行四边形又∵AC⊥BD∴四边形ABCD是菱形
学以致用
如图，ΔABC 为等腰三角形，把它沿底边BC 翻折后，得到ΔDBC．请你判断四边形ABDC 的形状，并说出你的理由．
课堂小结 3、菱形的判定定理
（1）四条边都相等的四边形是菱形
（2）对角线互相垂直的平行四边形是菱形 1、菱形的定义：一组邻边相等的平行四边形是菱形。 2、菱形的性质定理
（1）菱形的四条边都相等
（2）菱形的对角线互相垂直平分。3、证明：在 ABCD中,AD∥BC
又∵EF ∥AB
∴四边形ABEF是平行四边形∵AE平分∠BAD
∴∠1=∠2
∵AD ∥BC
∴∠2=∠3
∴∠1=∠3
∴AB=BE
∴四边形ABEF是菱形
1、3cm达标测试答案添加方式2：AC ⊥ BD2、添加方式1：AB=AD或AB=BC或BC=CD或CD=AD再见