人教版高中物理必修第二册 第6章 第4节 生活中的圆周运动(课件)(共31张PPT)
文档属性
| 名称 | 人教版高中物理必修第二册 第6章 第4节 生活中的圆周运动(课件)(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-07 13:50:30 | ||
图片预览









文档简介
(共31张PPT)
第6章 圆周运动
第4节 生活中的圆周运动
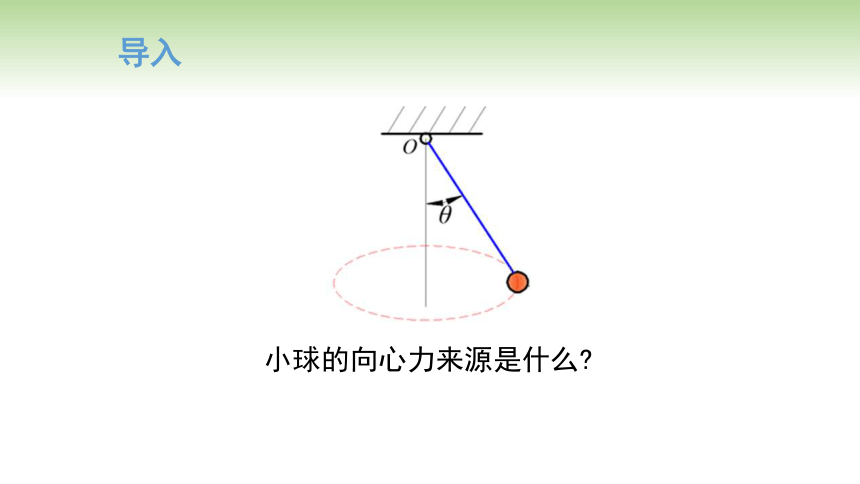
导入
小球的向心力来源是什么
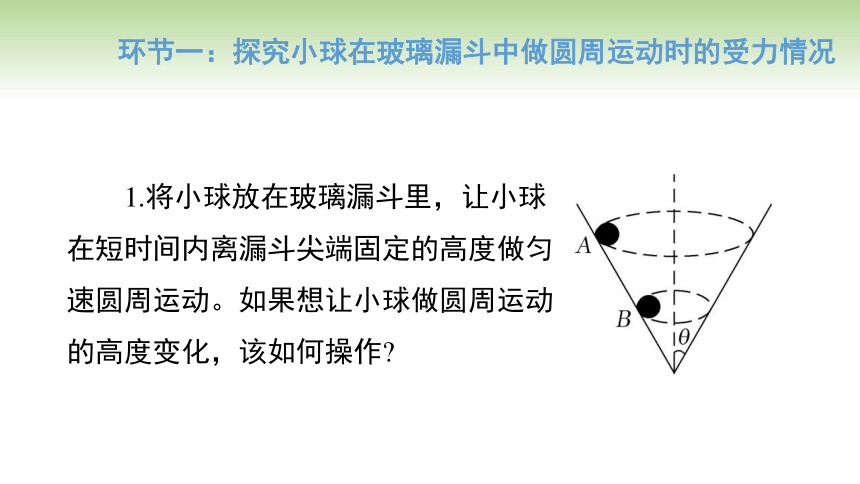
环节一:探究小球在玻璃漏斗中做圆周运动时的受力情况
1.将小球放在玻璃漏斗里,让小球在短时间内离漏斗尖端固定的高度做匀速圆周运动。如果想让小球做圆周运动的高度变化,该如何操作
环节一:探究小球在玻璃漏斗中做圆周运动时的受力情况
2.如果漏斗不动,小球主动转动,小球在固定高度做圆周运动的向心力由什么力提供 已知小球质量m,倾斜角度θ,运动半径r,A、B两位置的线速度大小是否相同 请解释小球做圆周运动的高度变化的原因。
环节一:探究小球在玻璃漏斗中做圆周运动时的受力情况
倾斜路面的好处是什么
环节二:分析水平面火车转弯过程的圆周运动
2022年对2013年7月24日西班牙列车脱轨的调查显示,这列火车脱轨的路段是一处急转弯,限速80 km/h,但当时列车的行驶速度是179 km/h。调查还显示,司机在事故发生前几秒钟接听了电话。司机的律师告诉媒体,事故发生地一段铁路路标丢失以及其他安全措施不足引发了脱轨,而不是接听电话。事故造成大约80人死亡,150人受伤。
环节二:分析水平面火车转弯过程的圆周运动
中国铁路经过第六次大提速,现在铁路主要干线上列车的速度已经提高到每小时200~250千米。其中京沪高铁可达到每小时380千米。如果你是铁路工程师,如何保证火车转弯安全的同时并减缓设施的老化
环节二:分析水平面火车转弯过程的圆周运动
在实际生活中火车的车轮和轨道有什么特点 若火车在水平轨道转弯,是否存在由于圆周运动产生对铁轨的挤压力 挤压内轨道还是外轨道
环节二:分析水平面火车转弯过程的圆周运动
我国自主研发的CR400AF电力动车组,最高运营速度达到350 km/h(约为100 m/s),8节车厢编组,总质量约为500吨,工程设计弯道最小曲线半径为5 000 m(可近似认为轨道转弯处的半径R=5 000 m)。若转弯处轨道是水平的,请计算动车以100 m/s的速度转弯时需要的向心力是多大 为了减少动车对轨道的挤压和避免事故,生活中动车转弯处的轨道结构有什么特点 此时动车向心力的来源是什么
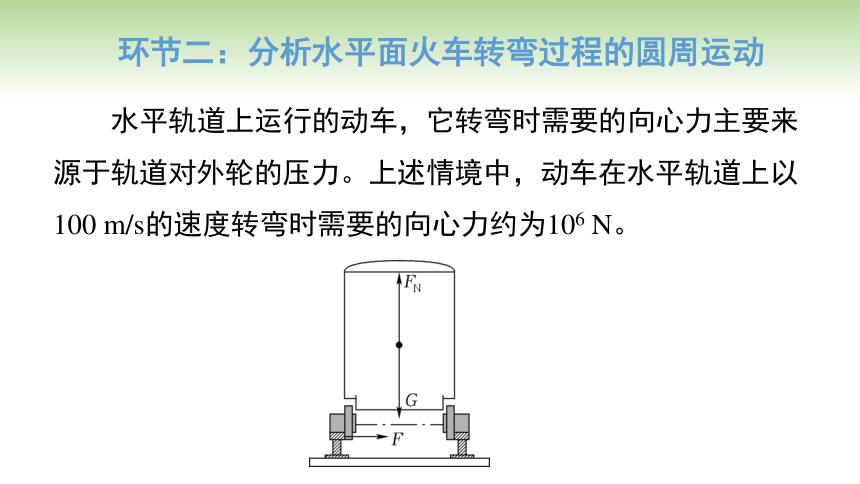
环节二:分析水平面火车转弯过程的圆周运动
水平轨道上运行的动车,它转弯时需要的向心力主要来源于轨道对外轮的压力。上述情境中,动车在水平轨道上以100 m/s的速度转弯时需要的向心力约为106 N。
环节二:分析水平面火车转弯过程的圆周运动
为了减少动车转弯对轨道的损害,设计时,在铁路的弯道处,内、外轨有高度差。
环节二:分析水平面火车转弯过程的圆周运动
若已知火车的质量m,轨道倾斜角度θ,转弯半径r。若火车对轨道没有挤压,求火车做匀速圆周运动的线速度大小。若火车转弯时大于这个速度,火车是否会像漏斗模型中的小球一样向上运动
mg
FN
F
θ
环节二:分析水平面火车转弯过程的圆周运动
(1)火车转弯时,若火车轮缘不受轨道压力,则mgtan θ= m,得v0= grtan θ。其中,r为弯道半径,θ为轨道所在平面与水平面的夹角,v0为弯道的规定速度。
(2)当火车速度v>v0时,火车有离心运动趋势,外轨与轮缘间存在侧向挤压力。
(3)当火车速度v环节三:利用凹凸桥模型,研究物体在竖直平面的圆周运动
当你骑自行车上学的途中,高速行驶做圆周运动的车轮碾过一个大坑时,坐在车座的你会有什么感受呢
将你和车的总质量设为m,凹形路面简化为一个半径为r的圆的一部分,可认为车在竖直平面内做圆周运动,当车经过凹形路面的最低点时速度为v,车的向心力由谁来提供 车对地面的压力有多大 车处于失重还是超重状态 人的感受如何
环节三:利用凹凸桥模型,研究物体在竖直平面的圆周运动
建立物理模型,做汽车过凹形路面的受力分析(如图所示)。
以向心力的方向为正方向,由牛顿第二定律得
FN-mg=m
解得FN=mg+m。
环节三:利用凹凸桥模型,研究物体在竖直平面的圆周运动
由牛顿第三定律可求出凹形路面受到的压力:
FN'=FN= mg+m>mg
可见,FN >mg,即汽车通过凹形路面时对路面的压力大于其所受的重力,处于超重状态,人感觉到了座椅对人向上的支持力。
汽车通过凹形路面时对路面的压力大于汽车的重力,并随着速度的增大而增大。
环节三:利用凹凸桥模型,研究物体在竖直平面的圆周运动
提示:在拱形桥的最高点,对汽车进行受力分析,确定向心力的来源;由牛顿第二定律列出方程求出汽车受到的支持力;由牛顿第三定律求出桥面受到的压力。
汽车通过拱形桥的最高点时,会出现什么情况呢
环节三:利用凹凸桥模型,研究物体在竖直平面的圆周运动
在拱形桥的最高点,对汽车进行受力分析,如图所示。
以向心力的方向为正方向,由牛顿第二定律得
mg-FN=m
解得FN=mg-m。
环节三:利用凹凸桥模型,研究物体在竖直平面的圆周运动
由牛顿第三定律求出拱形桥面受到的压力:
FN'=FN =mg-m
可见, FN环节三:利用凹凸桥模型,研究物体在竖直平面的圆周运动
汽车通过拱形桥的最高点时对桥面的压力FN'小于汽车的重力mg,并且压力随汽车速度的增大而减小。
当汽车对桥面的压力刚好减为0时,汽车的速度有多大 当汽车的速度大于这个速度时,会发生什么现象
可知当速度过快时,汽车可能离开桥面做平抛运动,非常危险。
环节四:航天器中的失重现象
当汽车的速度达到一定程度时,地面对车的支持力是0。这时驾驶员与座椅之间的压力是多少 驾驶员躯体各部分之间的压力是多少 他这时可能有什么感觉
环节四:航天器中的失重现象
分析航天员的受力情况可得mg-FN=m
解得FN=mg-m。
当mg=m时,解得v=。
即当v=时,座舱对航天员的支持力FN=0,航天员与座椅之间的压力、航天员躯体各部分之间的压力都是0,航天员处于完全失重状态。
环节四:航天器中的失重现象
环节五:了解生活中的离心运动
用不可伸长的细绳牵引着小球在光滑的水平面上做匀速圆周运动,当突然撤去绳子的拉力时,小球将怎样运动 若小球受的拉力小于小球需要的向心力,小球会如何运动呢
环节五:了解生活中的离心运动
(1)若F合=mω2r或F合=m,物体做匀速圆周运动,即“提供”满足“需要”。
(2)若F合>mω2r或F合>m,物体做半径变小的近心运动,即“提供过度”,也就是“提供”大于“需要”。
环节五:了解生活中的离心运动
(3)若F合< mω2r或F合环节五:了解生活中的离心运动
(4)若F合=0,则物体做直线运动。
注意:做圆周运动的物体,在向心力突然消失,或合力不足以提供向心力时,物体就会逐渐远离圆心运动,这种运动叫作离心运动。
环节五:了解生活中的离心运动
(1)应用:
①洗衣机脱水时,利用离心运动把附着在衣物上的水甩掉。
②在炼钢厂中,把熔化的钢水浇入圆柱形模子,模子沿圆柱的中心轴线高速旋转,钢水由于离心运动趋于周壁,冷却后就形成无缝钢管。
环节五:了解生活中的离心运动
(2)危害:
①在水平公路上行驶的汽车,如果转弯时速度过快,所需向心力F很大,大于最大静摩擦力Fm时,汽车将做离心运动而造成事故。
②高速转动的砂轮、飞轮等,都不得超过允许的最大转速。转速过高时,砂轮、飞轮内部分子间的相互作用力不足以提供所需向心力,离心运动会使它们破裂,酿成事故。
课堂练习
1.如图所示,长为L的悬线固定在O点,在O点正下方有一钉子C,O、C的距离为L2,把悬线另一端的小球A拉到跟悬点在同一水平面处无初速度释放,小球运动到悬点正下方,悬线碰到钉子瞬间 ( )
A.小球的线速度突然增大为原来的2倍
B.小球的加速度突然增大为原来的2倍
C.小球受的拉力突然增大为原来的2倍
D.小球的向心力突然增大为原来的4倍
B
课堂练习
2.火车轨道在转弯处外轨高于内轨,其高度差由转弯半径与火车速度确定。若在某转弯处规定行驶的速度为v,则下列说法中正确的是( )
①当火车以v的速度通过此弯路时,火车所受重力与轨道面支持力的合力提供向心力
②当火车以v的速度通过此弯路时,火车所受重力、轨道面支持力和外轨对轮缘弹力的合力提供向心力
③当火车速度大于v时,轮缘挤压外轨
④当火车速度小于v时,轮缘挤压外轨
A.①③ B.①④
C.②③ D.②④
A
第6章 圆周运动
第4节 生活中的圆周运动
导入
小球的向心力来源是什么
环节一:探究小球在玻璃漏斗中做圆周运动时的受力情况
1.将小球放在玻璃漏斗里,让小球在短时间内离漏斗尖端固定的高度做匀速圆周运动。如果想让小球做圆周运动的高度变化,该如何操作
环节一:探究小球在玻璃漏斗中做圆周运动时的受力情况
2.如果漏斗不动,小球主动转动,小球在固定高度做圆周运动的向心力由什么力提供 已知小球质量m,倾斜角度θ,运动半径r,A、B两位置的线速度大小是否相同 请解释小球做圆周运动的高度变化的原因。
环节一:探究小球在玻璃漏斗中做圆周运动时的受力情况
倾斜路面的好处是什么
环节二:分析水平面火车转弯过程的圆周运动
2022年对2013年7月24日西班牙列车脱轨的调查显示,这列火车脱轨的路段是一处急转弯,限速80 km/h,但当时列车的行驶速度是179 km/h。调查还显示,司机在事故发生前几秒钟接听了电话。司机的律师告诉媒体,事故发生地一段铁路路标丢失以及其他安全措施不足引发了脱轨,而不是接听电话。事故造成大约80人死亡,150人受伤。
环节二:分析水平面火车转弯过程的圆周运动
中国铁路经过第六次大提速,现在铁路主要干线上列车的速度已经提高到每小时200~250千米。其中京沪高铁可达到每小时380千米。如果你是铁路工程师,如何保证火车转弯安全的同时并减缓设施的老化
环节二:分析水平面火车转弯过程的圆周运动
在实际生活中火车的车轮和轨道有什么特点 若火车在水平轨道转弯,是否存在由于圆周运动产生对铁轨的挤压力 挤压内轨道还是外轨道
环节二:分析水平面火车转弯过程的圆周运动
我国自主研发的CR400AF电力动车组,最高运营速度达到350 km/h(约为100 m/s),8节车厢编组,总质量约为500吨,工程设计弯道最小曲线半径为5 000 m(可近似认为轨道转弯处的半径R=5 000 m)。若转弯处轨道是水平的,请计算动车以100 m/s的速度转弯时需要的向心力是多大 为了减少动车对轨道的挤压和避免事故,生活中动车转弯处的轨道结构有什么特点 此时动车向心力的来源是什么
环节二:分析水平面火车转弯过程的圆周运动
水平轨道上运行的动车,它转弯时需要的向心力主要来源于轨道对外轮的压力。上述情境中,动车在水平轨道上以100 m/s的速度转弯时需要的向心力约为106 N。
环节二:分析水平面火车转弯过程的圆周运动
为了减少动车转弯对轨道的损害,设计时,在铁路的弯道处,内、外轨有高度差。
环节二:分析水平面火车转弯过程的圆周运动
若已知火车的质量m,轨道倾斜角度θ,转弯半径r。若火车对轨道没有挤压,求火车做匀速圆周运动的线速度大小。若火车转弯时大于这个速度,火车是否会像漏斗模型中的小球一样向上运动
mg
FN
F
θ
环节二:分析水平面火车转弯过程的圆周运动
(1)火车转弯时,若火车轮缘不受轨道压力,则mgtan θ= m,得v0= grtan θ。其中,r为弯道半径,θ为轨道所在平面与水平面的夹角,v0为弯道的规定速度。
(2)当火车速度v>v0时,火车有离心运动趋势,外轨与轮缘间存在侧向挤压力。
(3)当火车速度v
当你骑自行车上学的途中,高速行驶做圆周运动的车轮碾过一个大坑时,坐在车座的你会有什么感受呢
将你和车的总质量设为m,凹形路面简化为一个半径为r的圆的一部分,可认为车在竖直平面内做圆周运动,当车经过凹形路面的最低点时速度为v,车的向心力由谁来提供 车对地面的压力有多大 车处于失重还是超重状态 人的感受如何
环节三:利用凹凸桥模型,研究物体在竖直平面的圆周运动
建立物理模型,做汽车过凹形路面的受力分析(如图所示)。
以向心力的方向为正方向,由牛顿第二定律得
FN-mg=m
解得FN=mg+m。
环节三:利用凹凸桥模型,研究物体在竖直平面的圆周运动
由牛顿第三定律可求出凹形路面受到的压力:
FN'=FN= mg+m>mg
可见,FN >mg,即汽车通过凹形路面时对路面的压力大于其所受的重力,处于超重状态,人感觉到了座椅对人向上的支持力。
汽车通过凹形路面时对路面的压力大于汽车的重力,并随着速度的增大而增大。
环节三:利用凹凸桥模型,研究物体在竖直平面的圆周运动
提示:在拱形桥的最高点,对汽车进行受力分析,确定向心力的来源;由牛顿第二定律列出方程求出汽车受到的支持力;由牛顿第三定律求出桥面受到的压力。
汽车通过拱形桥的最高点时,会出现什么情况呢
环节三:利用凹凸桥模型,研究物体在竖直平面的圆周运动
在拱形桥的最高点,对汽车进行受力分析,如图所示。
以向心力的方向为正方向,由牛顿第二定律得
mg-FN=m
解得FN=mg-m。
环节三:利用凹凸桥模型,研究物体在竖直平面的圆周运动
由牛顿第三定律求出拱形桥面受到的压力:
FN'=FN =mg-m
可见, FN
汽车通过拱形桥的最高点时对桥面的压力FN'小于汽车的重力mg,并且压力随汽车速度的增大而减小。
当汽车对桥面的压力刚好减为0时,汽车的速度有多大 当汽车的速度大于这个速度时,会发生什么现象
可知当速度过快时,汽车可能离开桥面做平抛运动,非常危险。
环节四:航天器中的失重现象
当汽车的速度达到一定程度时,地面对车的支持力是0。这时驾驶员与座椅之间的压力是多少 驾驶员躯体各部分之间的压力是多少 他这时可能有什么感觉
环节四:航天器中的失重现象
分析航天员的受力情况可得mg-FN=m
解得FN=mg-m。
当mg=m时,解得v=。
即当v=时,座舱对航天员的支持力FN=0,航天员与座椅之间的压力、航天员躯体各部分之间的压力都是0,航天员处于完全失重状态。
环节四:航天器中的失重现象
环节五:了解生活中的离心运动
用不可伸长的细绳牵引着小球在光滑的水平面上做匀速圆周运动,当突然撤去绳子的拉力时,小球将怎样运动 若小球受的拉力小于小球需要的向心力,小球会如何运动呢
环节五:了解生活中的离心运动
(1)若F合=mω2r或F合=m,物体做匀速圆周运动,即“提供”满足“需要”。
(2)若F合>mω2r或F合>m,物体做半径变小的近心运动,即“提供过度”,也就是“提供”大于“需要”。
环节五:了解生活中的离心运动
(3)若F合< mω2r或F合
(4)若F合=0,则物体做直线运动。
注意:做圆周运动的物体,在向心力突然消失,或合力不足以提供向心力时,物体就会逐渐远离圆心运动,这种运动叫作离心运动。
环节五:了解生活中的离心运动
(1)应用:
①洗衣机脱水时,利用离心运动把附着在衣物上的水甩掉。
②在炼钢厂中,把熔化的钢水浇入圆柱形模子,模子沿圆柱的中心轴线高速旋转,钢水由于离心运动趋于周壁,冷却后就形成无缝钢管。
环节五:了解生活中的离心运动
(2)危害:
①在水平公路上行驶的汽车,如果转弯时速度过快,所需向心力F很大,大于最大静摩擦力Fm时,汽车将做离心运动而造成事故。
②高速转动的砂轮、飞轮等,都不得超过允许的最大转速。转速过高时,砂轮、飞轮内部分子间的相互作用力不足以提供所需向心力,离心运动会使它们破裂,酿成事故。
课堂练习
1.如图所示,长为L的悬线固定在O点,在O点正下方有一钉子C,O、C的距离为L2,把悬线另一端的小球A拉到跟悬点在同一水平面处无初速度释放,小球运动到悬点正下方,悬线碰到钉子瞬间 ( )
A.小球的线速度突然增大为原来的2倍
B.小球的加速度突然增大为原来的2倍
C.小球受的拉力突然增大为原来的2倍
D.小球的向心力突然增大为原来的4倍
B
课堂练习
2.火车轨道在转弯处外轨高于内轨,其高度差由转弯半径与火车速度确定。若在某转弯处规定行驶的速度为v,则下列说法中正确的是( )
①当火车以v的速度通过此弯路时,火车所受重力与轨道面支持力的合力提供向心力
②当火车以v的速度通过此弯路时,火车所受重力、轨道面支持力和外轨对轮缘弹力的合力提供向心力
③当火车速度大于v时,轮缘挤压外轨
④当火车速度小于v时,轮缘挤压外轨
A.①③ B.①④
C.②③ D.②④
A
