人教版高中物理必修第二册 第8章 第3节 动能和动能定理(课件)(共19张PPT)
文档属性
| 名称 | 人教版高中物理必修第二册 第8章 第3节 动能和动能定理(课件)(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-07 14:49:32 | ||
图片预览




文档简介
(共19张PPT)
第8章 机械能守恒定律
第3节 动能和动能定理
图中的两名同学在做什么?
在射箭。
箭获得的动能从何而来?
弓的弹性势能转化成箭的
动能。
通过什么来发生这种转化
通过做功。弓发生形变而产生弹力,通过弓弦作用于箭,依靠弹力做功使箭获得动能。
导入
导入
两名同学射出的箭的“杀
伤”本领可能不同,实际是反
映了什么物理量的不同?
箭的动能大小的不同。
本节课我们就一起来研究
一下,动能的表达式是什么?
力对物体做的功与物体的动能之间又有什么定量关系?
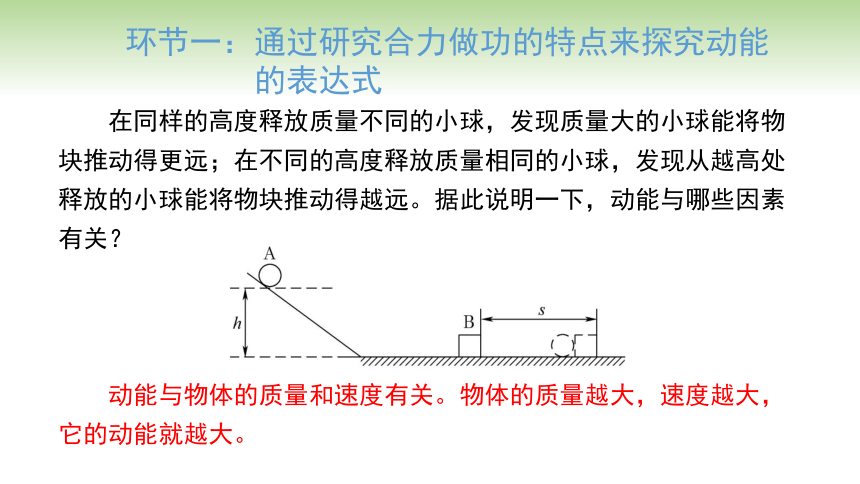
在同样的高度释放质量不同的小球,发现质量大的小球能将物块推动得更远;在不同的高度释放质量相同的小球,发现从越高处释放的小球能将物块推动得越远。据此说明一下,动能与哪些因素有关?
动能与物体的质量和速度有关。物体的质量越大,速度越大,它的动能就越大。
环节一:通过研究合力做功的特点来探究动能
的表达式
类比探究重力势能、弹性势能表达式的思路,该如何探究动能的表达式呢?
通过研究力做功的特点,来探究动能的表达式。
通过研究重力做功的特点,可以探究出重力势能的表达式;通过研究弹簧弹力做功的特点,可以探究出弹性势能的表达式。按照这样的思路,研究什么力做的功,有助于我们探究出动能的表达式呢?
合力做功。因为根据牛顿第二定律,由合力来产生加速度,而加速度又会影响速度的变化,而速度跟物体的动能有关,所以合力做的功与物体的动能有关。
环节一:通过研究合力做功的特点来探究动能
的表达式
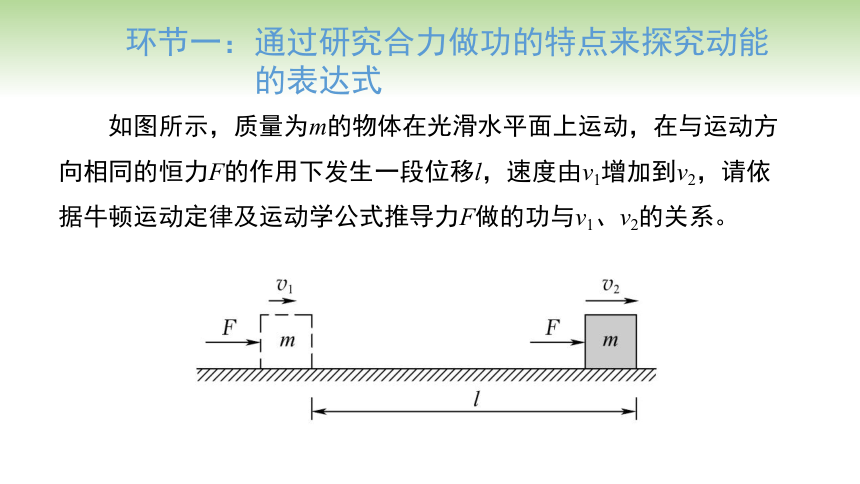
如图所示,质量为m的物体在光滑水平面上运动,在与运动方向相同的恒力F的作用下发生一段位移l,速度由v1增加到v2,请依据牛顿运动定律及运动学公式推导力F做的功与v1、v2的关系。
环节一:通过研究合力做功的特点来探究动能
的表达式
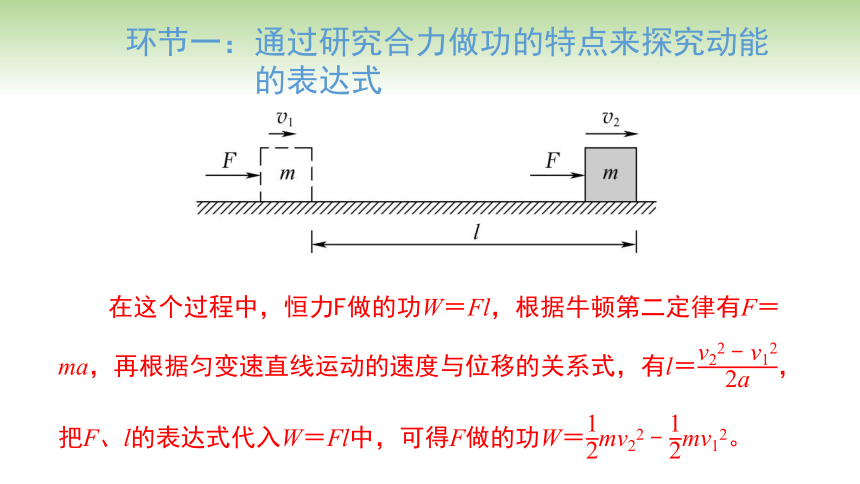
在这个过程中,恒力F做的功W=Fl,根据牛顿第二定律有F=ma,再根据匀变速直线运动的速度与位移的关系式,有l=,把F、l的表达式代入W=Fl中,可得F做的功W=mv22﹣mv12。
环节一:通过研究合力做功的特点来探究动能
的表达式
从前面的推导过程中,我们发现“mv2”很可能是一个具有特定意义的物理量。一方面,这个量在过程的末态与初态的差值正好等于力在这个过程中对物体做的功,而功是能量转化的量度,故这个量反映的是初态、末态都具有的同一形式的能量;另一方面,它正好跟物体动能的决定因素有关。因此,物理学中就用“mv2”表示物体的动能。
环节一:通过研究合力做功的特点来探究动能
的表达式
(1)动能是状态量,而功是过程量。
(2)动能是标量,且没有负值。
(3)动能具有相对性,与参考系的选取有关,通常选地面为参考系。
(4)动能与速度的辨析:
①物体的速度改变时,动能不一定发生改变。
②物体的动能改变时,速度一定发生了改变。
环节一:通过研究合力做功的特点来探究动能
的表达式
前面我们推导出的规律是否只适用于光滑水平面的情况呢?
质量为m的物体在粗糙的水
平面上运动,在恒力F和FN的作
用下发生一段位移L,速度由v1
变化到v2,请依据牛顿运动定律
及运动学公式推导动能的变化量
与什么力做的功有关。
环节二:对动能定理的深入理解
力在一个过程中对物体做的功,等于物体在这个过程中动能的变化,这个结论就是动能定理。
(1)因果关系,即做功导致动能变化。
(2)功能关系,即W合=ΔEk:
①当合力做正功时,动能增大;
②当合力做负功时,动能减小。
③合力做多少功,动能就变化多少。
(3)相对性,即功与动能均需要相对于同一参考系,通常选地面作为参考系。
环节二:对动能定理的深入理解
(4)动能定理是标量方程,不可以分解。
例如,研究平抛运动的规律时,速
度、位移、牛顿第二定律均可以分解为
水平方向和竖直方向来研究,但若对平
抛运动应用动能定理,则不能以水平方
向和竖直方向分解去列动能定理,只能
针对合运动而言列式:mgh=mv2﹣mv02。
环节二:对动能定理的深入理解
(5)普适性,即当物体受变力作用或做曲线运动时,动能定理仍成立。
可进行如下推导:
利用微元法,把整个过程分成许多小段,认为物体在每小段运动中受到的是恒力,运动的轨迹为直线,则有W1=mv12﹣mv02,W2=mv22﹣mv12,W3=mv32﹣mv22……Wn=mvn2﹣mvn﹣12。把这些小段中各力做的功相加,可以得到W=mvn2﹣mv02。
环节二:对动能定理的深入理解
例题 用F=20 N的水平推力推着质量为m=60 kg的冰车,使其由静止开始运动。冰车受到的摩擦力是它对冰面压力的0.01倍,当冰车前进s1=30 m后,撤去推力F,冰车又前进了一段距离后停止。g取10 m/s2。求:
(1)撤去推力F时冰车
的速度大小;
(2)冰车运动的总路程s。
环节三:动能定理的应用
应用动能定理解题的思维流程:
(1)确定研究对象及运动过程。
(2)分析物体在运动过程中的受力情况,明确每个力是否做功,是做正功还是做负功。
(3)明确初状态和末状态的动能,写出始、末状态动能的表达式。
(4)根据动能定理列原始方程并计算求解。
环节三:动能定理的应用
例题 半径为R的竖直半圆形轨道与水平轨道平滑衔接,固定在水平地面上,质量为m的小球以水平初速度v0=滚入轨道,重力加速度为g。
(1)若轨道处处光滑,判断小球
能否到达最高点。
(2)若轨道处处粗糙,小球恰能
通过最高点,求小球克服摩擦力做的功。
环节三:动能定理的应用
课堂练习
AC
课堂练习
C
课堂练习
3.如图甲所示的“滑滑梯”是小朋友们喜爱的游戏活动之一。“滑滑梯”可简化为图乙所示的模型,斜面滑道AB的倾角为θ=37°,AB的长度为l=4.0 m。一个质量为20 kg的小朋友(可视为质点)从A点由静止开始下滑,最后停在水平滑道BC上。设小朋友与滑道AB、BC间的动摩擦因数均为μ=0.5,且经过B点时小朋友的速度大小不变。忽略空气阻力,已知sin 37°=0.6,cos 37°=0.8,重力加速度g取10 m/s2。求:
(1)小朋友在斜面AB上下滑的过程中,重力做的功;
(2)小朋友在水平滑道上滑行的距离。
(1)小朋友在斜面AB上下滑的过程中,重力做的功WG=mglsin 37°=480 J。
(2)根据动能定理有mglsin 37°﹣μmglcos 37°﹣μmgx=0﹣0,
解得小朋友在水平滑道上滑行的距离x=1.6 m。
第8章 机械能守恒定律
第3节 动能和动能定理
图中的两名同学在做什么?
在射箭。
箭获得的动能从何而来?
弓的弹性势能转化成箭的
动能。
通过什么来发生这种转化
通过做功。弓发生形变而产生弹力,通过弓弦作用于箭,依靠弹力做功使箭获得动能。
导入
导入
两名同学射出的箭的“杀
伤”本领可能不同,实际是反
映了什么物理量的不同?
箭的动能大小的不同。
本节课我们就一起来研究
一下,动能的表达式是什么?
力对物体做的功与物体的动能之间又有什么定量关系?
在同样的高度释放质量不同的小球,发现质量大的小球能将物块推动得更远;在不同的高度释放质量相同的小球,发现从越高处释放的小球能将物块推动得越远。据此说明一下,动能与哪些因素有关?
动能与物体的质量和速度有关。物体的质量越大,速度越大,它的动能就越大。
环节一:通过研究合力做功的特点来探究动能
的表达式
类比探究重力势能、弹性势能表达式的思路,该如何探究动能的表达式呢?
通过研究力做功的特点,来探究动能的表达式。
通过研究重力做功的特点,可以探究出重力势能的表达式;通过研究弹簧弹力做功的特点,可以探究出弹性势能的表达式。按照这样的思路,研究什么力做的功,有助于我们探究出动能的表达式呢?
合力做功。因为根据牛顿第二定律,由合力来产生加速度,而加速度又会影响速度的变化,而速度跟物体的动能有关,所以合力做的功与物体的动能有关。
环节一:通过研究合力做功的特点来探究动能
的表达式
如图所示,质量为m的物体在光滑水平面上运动,在与运动方向相同的恒力F的作用下发生一段位移l,速度由v1增加到v2,请依据牛顿运动定律及运动学公式推导力F做的功与v1、v2的关系。
环节一:通过研究合力做功的特点来探究动能
的表达式
在这个过程中,恒力F做的功W=Fl,根据牛顿第二定律有F=ma,再根据匀变速直线运动的速度与位移的关系式,有l=,把F、l的表达式代入W=Fl中,可得F做的功W=mv22﹣mv12。
环节一:通过研究合力做功的特点来探究动能
的表达式
从前面的推导过程中,我们发现“mv2”很可能是一个具有特定意义的物理量。一方面,这个量在过程的末态与初态的差值正好等于力在这个过程中对物体做的功,而功是能量转化的量度,故这个量反映的是初态、末态都具有的同一形式的能量;另一方面,它正好跟物体动能的决定因素有关。因此,物理学中就用“mv2”表示物体的动能。
环节一:通过研究合力做功的特点来探究动能
的表达式
(1)动能是状态量,而功是过程量。
(2)动能是标量,且没有负值。
(3)动能具有相对性,与参考系的选取有关,通常选地面为参考系。
(4)动能与速度的辨析:
①物体的速度改变时,动能不一定发生改变。
②物体的动能改变时,速度一定发生了改变。
环节一:通过研究合力做功的特点来探究动能
的表达式
前面我们推导出的规律是否只适用于光滑水平面的情况呢?
质量为m的物体在粗糙的水
平面上运动,在恒力F和FN的作
用下发生一段位移L,速度由v1
变化到v2,请依据牛顿运动定律
及运动学公式推导动能的变化量
与什么力做的功有关。
环节二:对动能定理的深入理解
力在一个过程中对物体做的功,等于物体在这个过程中动能的变化,这个结论就是动能定理。
(1)因果关系,即做功导致动能变化。
(2)功能关系,即W合=ΔEk:
①当合力做正功时,动能增大;
②当合力做负功时,动能减小。
③合力做多少功,动能就变化多少。
(3)相对性,即功与动能均需要相对于同一参考系,通常选地面作为参考系。
环节二:对动能定理的深入理解
(4)动能定理是标量方程,不可以分解。
例如,研究平抛运动的规律时,速
度、位移、牛顿第二定律均可以分解为
水平方向和竖直方向来研究,但若对平
抛运动应用动能定理,则不能以水平方
向和竖直方向分解去列动能定理,只能
针对合运动而言列式:mgh=mv2﹣mv02。
环节二:对动能定理的深入理解
(5)普适性,即当物体受变力作用或做曲线运动时,动能定理仍成立。
可进行如下推导:
利用微元法,把整个过程分成许多小段,认为物体在每小段运动中受到的是恒力,运动的轨迹为直线,则有W1=mv12﹣mv02,W2=mv22﹣mv12,W3=mv32﹣mv22……Wn=mvn2﹣mvn﹣12。把这些小段中各力做的功相加,可以得到W=mvn2﹣mv02。
环节二:对动能定理的深入理解
例题 用F=20 N的水平推力推着质量为m=60 kg的冰车,使其由静止开始运动。冰车受到的摩擦力是它对冰面压力的0.01倍,当冰车前进s1=30 m后,撤去推力F,冰车又前进了一段距离后停止。g取10 m/s2。求:
(1)撤去推力F时冰车
的速度大小;
(2)冰车运动的总路程s。
环节三:动能定理的应用
应用动能定理解题的思维流程:
(1)确定研究对象及运动过程。
(2)分析物体在运动过程中的受力情况,明确每个力是否做功,是做正功还是做负功。
(3)明确初状态和末状态的动能,写出始、末状态动能的表达式。
(4)根据动能定理列原始方程并计算求解。
环节三:动能定理的应用
例题 半径为R的竖直半圆形轨道与水平轨道平滑衔接,固定在水平地面上,质量为m的小球以水平初速度v0=滚入轨道,重力加速度为g。
(1)若轨道处处光滑,判断小球
能否到达最高点。
(2)若轨道处处粗糙,小球恰能
通过最高点,求小球克服摩擦力做的功。
环节三:动能定理的应用
课堂练习
AC
课堂练习
C
课堂练习
3.如图甲所示的“滑滑梯”是小朋友们喜爱的游戏活动之一。“滑滑梯”可简化为图乙所示的模型,斜面滑道AB的倾角为θ=37°,AB的长度为l=4.0 m。一个质量为20 kg的小朋友(可视为质点)从A点由静止开始下滑,最后停在水平滑道BC上。设小朋友与滑道AB、BC间的动摩擦因数均为μ=0.5,且经过B点时小朋友的速度大小不变。忽略空气阻力,已知sin 37°=0.6,cos 37°=0.8,重力加速度g取10 m/s2。求:
(1)小朋友在斜面AB上下滑的过程中,重力做的功;
(2)小朋友在水平滑道上滑行的距离。
(1)小朋友在斜面AB上下滑的过程中,重力做的功WG=mglsin 37°=480 J。
(2)根据动能定理有mglsin 37°﹣μmglcos 37°﹣μmgx=0﹣0,
解得小朋友在水平滑道上滑行的距离x=1.6 m。
