人教版高中物理必修第二册 第8章 第2节 重力势能(课件)(共32张PPT)
文档属性
| 名称 | 人教版高中物理必修第二册 第8章 第2节 重力势能(课件)(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 21.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-07 14:56:39 | ||
图片预览










文档简介
(共32张PPT)
第8章 机械能守恒定律
第2节 重力势能
导入一
高空抛物现象曾被称为“悬在城市上空的痛”。高空抛物,是一种不文明的行为,而且会带来很大的社会危害。有数据表明:一枚60g的鸡蛋从4楼抛下就会让人起肿包;从8楼抛下就可以让人头皮破损;从18楼抛下就可以砸破行人的头骨;从25楼抛下可使人当场死亡。
2019年11月,最高人民法院印发《关于依法妥善审理高空抛物、坠物案件的意见》,明确对于故意高空抛物者,根据具体情形按照以危险方法危害公共安全罪、故意伤害罪或故意杀人罪论处。
导入一
2021年2月,《最高人民法院、最高人民检察院关于执行<中华人民共和国刑法>确定罪名的补充规定(七)》规定了“高空抛物罪”罪名。
2021年3月1日,《中华人民共和国刑法修正案(十一)》生效,“高空抛物”正式入刑。
从物理学的视角看,一枚小小的鸡蛋,它所处的位置越高,它具有的重力势能就越大,它的“杀伤力”就会越大。那么,重力势能的表达式是什么呢?
导入一
导入二
一枚鸡蛋从30 m高的高空坠下能砸碎玻璃,你觉得这是真的吗?
从物理学的视角看,一枚小小的鸡蛋,它所处的位置越高,它具有的重力势能就越大,它的“杀伤力”就会越大。那么,重力势能的表达式是什么呢?
导入二
请同学们根据前面提到的现象,分析一下,重力势能的大小与哪些因素有关?
重力势能的大小与物体的质量和所处的高度有关。物体的质量越大,所处的位置越高,重力势能就越大。
重力势能用字母Ep表示,请大家猜测一下, Ep与m、h之间的关系式是什么呢?
可能是Ep =mgh、Ep=mgh2、Ep=m2g2h、Ep=mgh3……
环节一:通过研究重力做功的特点来探究重力
势能的表达式
要想明确重力势能的表达式,还需要进行定量推导。从什么角度入手呢?由于功和能的变化是紧密联系的,我们可以从研究功入手。那么,研究什么力的功呢?
前面我们注意到重力势能随高度的变化而变化,而当物体的高度变化时,必定对应着重力做功。当物体下降时,重力做正功,势能减小;当物体被举高时,重力做负功,势能增大。因此,重力势能与重力做功密切相关,研究重力势能的表达式可以从推导重力做功的特点入手。
环节一:通过研究重力做功的特点来探究重力
势能的表达式
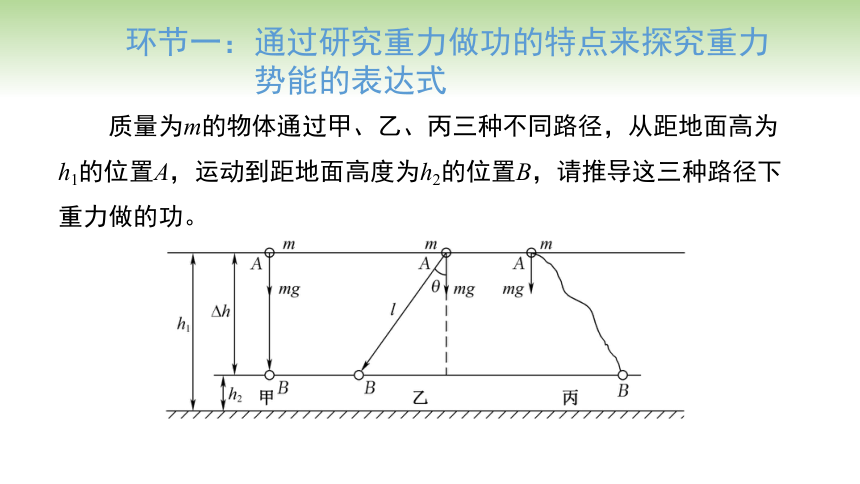
质量为m的物体通过甲、乙、丙三种不同路径,从距地面高为h1的位置A,运动到距地面高度为h2的位置B,请推导这三种路径下重力做的功。
环节一:通过研究重力做功的特点来探究重力
势能的表达式
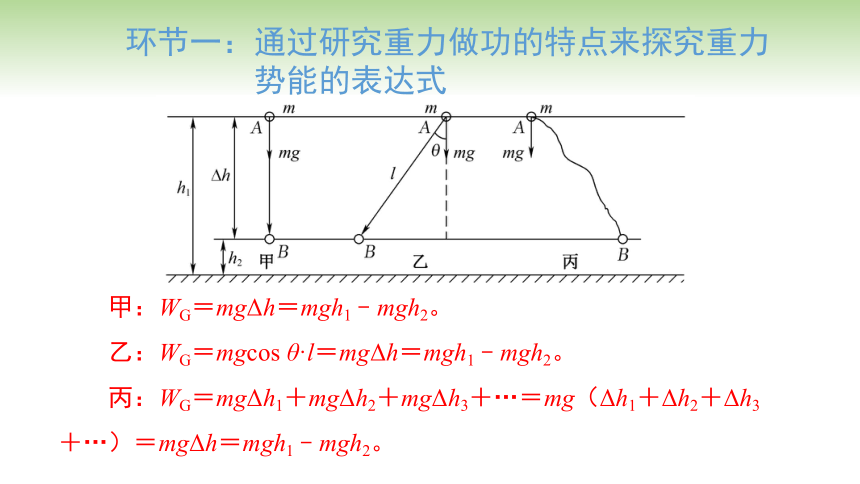
甲:WG=mgΔh=mgh1﹣mgh2。
乙:WG=mgcos θ·l=mgΔh=mgh1﹣mgh2。
丙:WG=mgΔh1+mgΔh2+mgΔh3+…=mg(Δh1+Δh2+Δh3+…)=mgΔh=mgh1﹣mgh2。
环节一:通过研究重力做功的特点来探究重力
势能的表达式
分析丙情境时,可以利用微元法的思想,把曲面看成由很多段小斜面组成,利用乙情境的结论可以得出,重力做功仍然只由始、末位置的高度差决定。
重力做功的特点:物体运动时,重力对它做的功只跟它的起点和终点的位置有关,而跟物体运动的路径无关。
环节一:通过研究重力做功的特点来探究重力
势能的表达式
重力做的功只与重力跟起点高度的乘积mgh1、重力跟终点高度的乘积mgh2两者之差有关。看来,物体的重力mg跟它所处位置的高度h的乘积mgh,具有特殊的意义。
一方面,mgh与重力做的功密切相关,反映着确定位置所具有的确定的状态量;另一方面,它随着高度的增加而增加,随着质量的增大而增大,恰好与前述重力势能的特征一致。因此,我们就把mgh叫作物体的重力势能,即Ep=mgh。
环节一:通过研究重力做功的特点来探究重力
势能的表达式
请大家思考下列问题:
(1)重力势能是属于谁的?
(2)重力势能的单位是什么?
(3)重力势能是标量还是矢量?
(4)重力势能有正、负吗?若有,则正、负代表什么含义?
注意:物体的重力势能总是相对于某一水平面来说的,这个水平面叫作参考平面。在这个水平面上,物体的重力势能取为0。参考平面的选择是任意的,可视研究问题的方便而定。
环节二:对重力势能概念的深入理解
如图所示,小球的质量为m,从A点落到地面上的B点。
(1)若下落过程中存在阻力,表格中的数据是否会
发生改变?
(2)重力势能与重力势能的变化量是同一含义吗?
重力做功与重力势能的变化量有什么关系?
环节二:对重力势能概念的深入理解
(1)重力势能具有系统性。重力势能是属于物体和地球所组成的系统的。如果没有地球对物体的吸引,就不会有重力做功,也就不存在重力势能,所以重力势能是属于系统的。
(2)重力势能的单位是焦耳,符号为J。1 J=1 kg·m·s﹣2·m=
1 N·m。
(3)重力势能是标量。
环节二:对重力势能概念的深入理解
(4)重力势能具有正、负。因为表达式中的h是相对于参考平面(零势能面)的高度,而参考平面的选择是任意的。若物体位于参考平面之上,则重力势能为正值;若物体位于参考平面之下,则重力势能为负值。因此,重力势能的正、负代表大小。
环节二:对重力势能概念的深入理解
(5)重力势能与重力势能的变化量含义不同。
①重力势能表示物体在一个位置的状态值,而重力势能的变化量表示物体在两个状态之间的差量。
②重力势能具有相对性,与参考面的选择有关;而重力势能的变化量具有绝对性,与参考面的选择无关。因此,相较于重力势能,重力势能的变化量更有意义。
③重力做功与重力势能的变化量互为相反数,这种功能关系与其他力无关。
环节二:对重力势能概念的深入理解
请大家从定义式的角度,推导重力做功与重力势能变化量为什么是互为相反数的关系。
WG12=mgΔh=mgh1﹣mgh2,
ΔEp12=Ep2﹣Ep1=mgh2﹣mgh1,
联立可得WG=﹣ΔEp。
环节三:重力势能变化量与重力做功的关系
请大家从正、负的角度,理解重力做功与重力势能变化量为什么是互为相反数的关系。
(1)当物体由高处运动到低处时,重力做正功,重力势能减小,即WG>0时ΔEp<0。
(2)当物体由低处运动到高处时,重力做负功,重力势能增大,即WG<0时ΔEp>0。
(3)但从绝对值上看,WG和ΔEp都是只由mgΔh决定的。
环节三:重力势能变化量与重力做功的关系
例题 以下说法是否正确?如果正确,说出一种可能的实际情况;如果不正确,说明这种说法为什么错误。
(1)物体受拉力作用向上运动,拉力做的功是1 J,但物体重力势能的增加量不是1 J。
(2)物体受拉力作用向上匀速运动,拉力做功是1 J,但物体重力势能的增加量不是1 J。
(3)物体运动,重力做的功是﹣1 J,但物体重力势能的增加量不是1 J。
(4)没有摩擦时,物体由A沿直线运动到B,重力做的功是﹣1 J;有摩擦时,物体由A沿曲线运动到B,重力做的功大于﹣1 J。
环节三:重力势能变化量与重力做功的关系
观察下列图片,说一说,里面的哪些物体具有弹性势能?
撑竿跳高运动员手中弯曲的竿、射箭运动员手中被拉弯的弓、跳水运动员脚下被压弯的跳板等都具有弹性势能。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能。
请同学们猜测一下,弹性势能的大小与哪些因素有关?你的猜测依据是什么?
弹性势能跟形变的大小有关。例如,弹簧的形变量越大,在恢复原状的过程中能够对外做的功就越多,说明弹簧的弹性势能越大。另外,弹性势能还跟弹簧的劲度系数有关。例如,不同的弹簧,如果发生相同的形变,劲度系数越大的,在恢复原状的过程中对外做的功就越多,因而弹性势能越大。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
用什么方法能够定量探究弹性势能的表达式呢?
仿照重力势能的研究方法,可以通过研究弹力做功的特点来研究弹性势能的表达式。
定义重力势能这一概念是源于重力做功与路径无关,只与始、末位置有关。类似的,若要定义弹性势能这一概念,我们是不是就要先论证弹力做功是否也具有“与路径无关,只与始、末位置有关”的特点?如果弹力做功也具有这个特点,才能定义弹性势能,也就能通过功能关系寻找到弹性势能的表达式。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
如图所示,弹簧一端固定,另一端连接质量为m的物块(视为质点),在水平桌面上沿x轴运动,
理想弹簧的劲度系数为k,以弹簧原
长时物块的位置为坐标原点O。
(1)讨论沿两种不同路径,物块从x1位置运动到x2,弹力做的功。
路径①:x1→x2;
路径②:x1→x3→x2。
(2)弹力做功是否与路径有关?能否定义弹性势能?猜测一下,弹性势能的表达式是怎样的?
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
(1)利用弹力随物块运动的位移变化的F-x图像,利
用图像与x轴所围图形的面积来求弹力的功(如图所示)。
路径①:W12=﹣(kx1+kx2)(x2﹣x1)=kx12﹣kx22。
路径②:W13=﹣(kx1+kx3)(x3﹣x1)=kx12﹣kx32,
W32=(kx2+kx3)(x3﹣x2)=kx32﹣kx22,
W12=W13+W32=kx12﹣kx22。
(2)弹簧弹力做功与路径无关,只与始、末位置有关。猜测弹性势能的表达式为Ep=kx2,x为弹簧的形变量。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
注意:
(1)利用F-x图像中图线与坐标轴所围图形的面积求解弹力功,要注意x的本质含义为物体的位移,而非弹簧的形变量,因为力对位移的积累效果才是功。
(2)“kx2”之所以有意义,一方面是因为弹力做功与路径无关,只与初、末状态的“kx2”有关,说明它能反映初、末状态由相对位置决定的一种形式的能量;另一方面“kx2”与“弹性势能随着劲度系数的增大而增大、随着形变量的增大而增大”的特征一致。因此,把“kx2”定义为弹性势能的表达式。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
弹力做功与弹性势能的变化量之间有什么关系?
互为相反数。W12=kx12﹣kx22,ΔEp=kx22﹣kx12,所以
W弹=﹣ΔEp弹。
尝试利用上述问题情境,从W弹与ΔEp弹的正、负的角度,再来分析一下它们为什么互为相反数。
当物块由x1向x2运动时,弹力做负功,而弹性势能是增大的,即W弹<0,ΔEp弹>0;而当物块由x3向x2运动时,弹力做正功,而弹性势能是减小的,即W弹>0,ΔEp弹<0。同理,弹簧处于压缩状态时也有同样的规律。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
无论是重力势能还是弹性势能,我们都是通过研究相应力做功的特点来定义势能的,只有当力做功与路径无关,只与始、末位置有关时,才能定义相应的势能。
势能也叫位能,与相互作用的物体的相对位置有关。重力势能是由地球和地面上物体的相对位置决定的,弹性势能是由发生弹性形变的物体各部分的相对位置决定的。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
若在前述问题中,物块与水平面之间的动摩擦因数为μ,物块由x1向右运动到x3,然后由x3返回到x2,在这个过程中,分析滑动摩擦力做功的特点,说明是否存在“摩擦力势能”的概念。
摩擦力做的功Wf=﹣μmg(x3﹣x1)﹣μmg(x3﹣x2)=﹣μmg(2x3﹣
x1﹣x2)。
摩擦力做功与路径有关,不是只与始、末位置有关,故每个位置没有与摩擦力对应的确定势能,不存在“摩擦力势能”的概念。
环节五:若某个力做功与路径有关还能否定义
相应的势能
课堂练习
BCD
课堂练习
BD
课堂练习
3.如图所示,质量为m的足球从地面上的位置1被踢出后落到地面上的位置3,在空中达到的最高点为位置2,且其高度为h。重力加速度为g。
(1)若选择地面作为零势能面,则足球在位置2的重力势能是多大 若选择最高点作为零势能面,则足球在位置3的重力势能是多大
(2)足球由位置1运动到位置2的过程中,重力做了多少功 足球的重力势能变化了多少
(3)足球由位置2运动到位置3的过程中,重力做了多少功 足球的重力势能变化了多少
(4)足球由位置1运动到位置3的过程中,重力做了多少功
(1)mgh ﹣mgh (2)﹣mgh mgh (3)mgh ﹣mgh (4)0
第8章 机械能守恒定律
第2节 重力势能
导入一
高空抛物现象曾被称为“悬在城市上空的痛”。高空抛物,是一种不文明的行为,而且会带来很大的社会危害。有数据表明:一枚60g的鸡蛋从4楼抛下就会让人起肿包;从8楼抛下就可以让人头皮破损;从18楼抛下就可以砸破行人的头骨;从25楼抛下可使人当场死亡。
2019年11月,最高人民法院印发《关于依法妥善审理高空抛物、坠物案件的意见》,明确对于故意高空抛物者,根据具体情形按照以危险方法危害公共安全罪、故意伤害罪或故意杀人罪论处。
导入一
2021年2月,《最高人民法院、最高人民检察院关于执行<中华人民共和国刑法>确定罪名的补充规定(七)》规定了“高空抛物罪”罪名。
2021年3月1日,《中华人民共和国刑法修正案(十一)》生效,“高空抛物”正式入刑。
从物理学的视角看,一枚小小的鸡蛋,它所处的位置越高,它具有的重力势能就越大,它的“杀伤力”就会越大。那么,重力势能的表达式是什么呢?
导入一
导入二
一枚鸡蛋从30 m高的高空坠下能砸碎玻璃,你觉得这是真的吗?
从物理学的视角看,一枚小小的鸡蛋,它所处的位置越高,它具有的重力势能就越大,它的“杀伤力”就会越大。那么,重力势能的表达式是什么呢?
导入二
请同学们根据前面提到的现象,分析一下,重力势能的大小与哪些因素有关?
重力势能的大小与物体的质量和所处的高度有关。物体的质量越大,所处的位置越高,重力势能就越大。
重力势能用字母Ep表示,请大家猜测一下, Ep与m、h之间的关系式是什么呢?
可能是Ep =mgh、Ep=mgh2、Ep=m2g2h、Ep=mgh3……
环节一:通过研究重力做功的特点来探究重力
势能的表达式
要想明确重力势能的表达式,还需要进行定量推导。从什么角度入手呢?由于功和能的变化是紧密联系的,我们可以从研究功入手。那么,研究什么力的功呢?
前面我们注意到重力势能随高度的变化而变化,而当物体的高度变化时,必定对应着重力做功。当物体下降时,重力做正功,势能减小;当物体被举高时,重力做负功,势能增大。因此,重力势能与重力做功密切相关,研究重力势能的表达式可以从推导重力做功的特点入手。
环节一:通过研究重力做功的特点来探究重力
势能的表达式
质量为m的物体通过甲、乙、丙三种不同路径,从距地面高为h1的位置A,运动到距地面高度为h2的位置B,请推导这三种路径下重力做的功。
环节一:通过研究重力做功的特点来探究重力
势能的表达式
甲:WG=mgΔh=mgh1﹣mgh2。
乙:WG=mgcos θ·l=mgΔh=mgh1﹣mgh2。
丙:WG=mgΔh1+mgΔh2+mgΔh3+…=mg(Δh1+Δh2+Δh3+…)=mgΔh=mgh1﹣mgh2。
环节一:通过研究重力做功的特点来探究重力
势能的表达式
分析丙情境时,可以利用微元法的思想,把曲面看成由很多段小斜面组成,利用乙情境的结论可以得出,重力做功仍然只由始、末位置的高度差决定。
重力做功的特点:物体运动时,重力对它做的功只跟它的起点和终点的位置有关,而跟物体运动的路径无关。
环节一:通过研究重力做功的特点来探究重力
势能的表达式
重力做的功只与重力跟起点高度的乘积mgh1、重力跟终点高度的乘积mgh2两者之差有关。看来,物体的重力mg跟它所处位置的高度h的乘积mgh,具有特殊的意义。
一方面,mgh与重力做的功密切相关,反映着确定位置所具有的确定的状态量;另一方面,它随着高度的增加而增加,随着质量的增大而增大,恰好与前述重力势能的特征一致。因此,我们就把mgh叫作物体的重力势能,即Ep=mgh。
环节一:通过研究重力做功的特点来探究重力
势能的表达式
请大家思考下列问题:
(1)重力势能是属于谁的?
(2)重力势能的单位是什么?
(3)重力势能是标量还是矢量?
(4)重力势能有正、负吗?若有,则正、负代表什么含义?
注意:物体的重力势能总是相对于某一水平面来说的,这个水平面叫作参考平面。在这个水平面上,物体的重力势能取为0。参考平面的选择是任意的,可视研究问题的方便而定。
环节二:对重力势能概念的深入理解
如图所示,小球的质量为m,从A点落到地面上的B点。
(1)若下落过程中存在阻力,表格中的数据是否会
发生改变?
(2)重力势能与重力势能的变化量是同一含义吗?
重力做功与重力势能的变化量有什么关系?
环节二:对重力势能概念的深入理解
(1)重力势能具有系统性。重力势能是属于物体和地球所组成的系统的。如果没有地球对物体的吸引,就不会有重力做功,也就不存在重力势能,所以重力势能是属于系统的。
(2)重力势能的单位是焦耳,符号为J。1 J=1 kg·m·s﹣2·m=
1 N·m。
(3)重力势能是标量。
环节二:对重力势能概念的深入理解
(4)重力势能具有正、负。因为表达式中的h是相对于参考平面(零势能面)的高度,而参考平面的选择是任意的。若物体位于参考平面之上,则重力势能为正值;若物体位于参考平面之下,则重力势能为负值。因此,重力势能的正、负代表大小。
环节二:对重力势能概念的深入理解
(5)重力势能与重力势能的变化量含义不同。
①重力势能表示物体在一个位置的状态值,而重力势能的变化量表示物体在两个状态之间的差量。
②重力势能具有相对性,与参考面的选择有关;而重力势能的变化量具有绝对性,与参考面的选择无关。因此,相较于重力势能,重力势能的变化量更有意义。
③重力做功与重力势能的变化量互为相反数,这种功能关系与其他力无关。
环节二:对重力势能概念的深入理解
请大家从定义式的角度,推导重力做功与重力势能变化量为什么是互为相反数的关系。
WG12=mgΔh=mgh1﹣mgh2,
ΔEp12=Ep2﹣Ep1=mgh2﹣mgh1,
联立可得WG=﹣ΔEp。
环节三:重力势能变化量与重力做功的关系
请大家从正、负的角度,理解重力做功与重力势能变化量为什么是互为相反数的关系。
(1)当物体由高处运动到低处时,重力做正功,重力势能减小,即WG>0时ΔEp<0。
(2)当物体由低处运动到高处时,重力做负功,重力势能增大,即WG<0时ΔEp>0。
(3)但从绝对值上看,WG和ΔEp都是只由mgΔh决定的。
环节三:重力势能变化量与重力做功的关系
例题 以下说法是否正确?如果正确,说出一种可能的实际情况;如果不正确,说明这种说法为什么错误。
(1)物体受拉力作用向上运动,拉力做的功是1 J,但物体重力势能的增加量不是1 J。
(2)物体受拉力作用向上匀速运动,拉力做功是1 J,但物体重力势能的增加量不是1 J。
(3)物体运动,重力做的功是﹣1 J,但物体重力势能的增加量不是1 J。
(4)没有摩擦时,物体由A沿直线运动到B,重力做的功是﹣1 J;有摩擦时,物体由A沿曲线运动到B,重力做的功大于﹣1 J。
环节三:重力势能变化量与重力做功的关系
观察下列图片,说一说,里面的哪些物体具有弹性势能?
撑竿跳高运动员手中弯曲的竿、射箭运动员手中被拉弯的弓、跳水运动员脚下被压弯的跳板等都具有弹性势能。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫作弹性势能。
请同学们猜测一下,弹性势能的大小与哪些因素有关?你的猜测依据是什么?
弹性势能跟形变的大小有关。例如,弹簧的形变量越大,在恢复原状的过程中能够对外做的功就越多,说明弹簧的弹性势能越大。另外,弹性势能还跟弹簧的劲度系数有关。例如,不同的弹簧,如果发生相同的形变,劲度系数越大的,在恢复原状的过程中对外做的功就越多,因而弹性势能越大。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
用什么方法能够定量探究弹性势能的表达式呢?
仿照重力势能的研究方法,可以通过研究弹力做功的特点来研究弹性势能的表达式。
定义重力势能这一概念是源于重力做功与路径无关,只与始、末位置有关。类似的,若要定义弹性势能这一概念,我们是不是就要先论证弹力做功是否也具有“与路径无关,只与始、末位置有关”的特点?如果弹力做功也具有这个特点,才能定义弹性势能,也就能通过功能关系寻找到弹性势能的表达式。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
如图所示,弹簧一端固定,另一端连接质量为m的物块(视为质点),在水平桌面上沿x轴运动,
理想弹簧的劲度系数为k,以弹簧原
长时物块的位置为坐标原点O。
(1)讨论沿两种不同路径,物块从x1位置运动到x2,弹力做的功。
路径①:x1→x2;
路径②:x1→x3→x2。
(2)弹力做功是否与路径有关?能否定义弹性势能?猜测一下,弹性势能的表达式是怎样的?
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
(1)利用弹力随物块运动的位移变化的F-x图像,利
用图像与x轴所围图形的面积来求弹力的功(如图所示)。
路径①:W12=﹣(kx1+kx2)(x2﹣x1)=kx12﹣kx22。
路径②:W13=﹣(kx1+kx3)(x3﹣x1)=kx12﹣kx32,
W32=(kx2+kx3)(x3﹣x2)=kx32﹣kx22,
W12=W13+W32=kx12﹣kx22。
(2)弹簧弹力做功与路径无关,只与始、末位置有关。猜测弹性势能的表达式为Ep=kx2,x为弹簧的形变量。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
注意:
(1)利用F-x图像中图线与坐标轴所围图形的面积求解弹力功,要注意x的本质含义为物体的位移,而非弹簧的形变量,因为力对位移的积累效果才是功。
(2)“kx2”之所以有意义,一方面是因为弹力做功与路径无关,只与初、末状态的“kx2”有关,说明它能反映初、末状态由相对位置决定的一种形式的能量;另一方面“kx2”与“弹性势能随着劲度系数的增大而增大、随着形变量的增大而增大”的特征一致。因此,把“kx2”定义为弹性势能的表达式。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
弹力做功与弹性势能的变化量之间有什么关系?
互为相反数。W12=kx12﹣kx22,ΔEp=kx22﹣kx12,所以
W弹=﹣ΔEp弹。
尝试利用上述问题情境,从W弹与ΔEp弹的正、负的角度,再来分析一下它们为什么互为相反数。
当物块由x1向x2运动时,弹力做负功,而弹性势能是增大的,即W弹<0,ΔEp弹>0;而当物块由x3向x2运动时,弹力做正功,而弹性势能是减小的,即W弹>0,ΔEp弹<0。同理,弹簧处于压缩状态时也有同样的规律。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
无论是重力势能还是弹性势能,我们都是通过研究相应力做功的特点来定义势能的,只有当力做功与路径无关,只与始、末位置有关时,才能定义相应的势能。
势能也叫位能,与相互作用的物体的相对位置有关。重力势能是由地球和地面上物体的相对位置决定的,弹性势能是由发生弹性形变的物体各部分的相对位置决定的。
环节四:通过研究弹簧弹力做功的特点来探究
弹性势能的表达式
若在前述问题中,物块与水平面之间的动摩擦因数为μ,物块由x1向右运动到x3,然后由x3返回到x2,在这个过程中,分析滑动摩擦力做功的特点,说明是否存在“摩擦力势能”的概念。
摩擦力做的功Wf=﹣μmg(x3﹣x1)﹣μmg(x3﹣x2)=﹣μmg(2x3﹣
x1﹣x2)。
摩擦力做功与路径有关,不是只与始、末位置有关,故每个位置没有与摩擦力对应的确定势能,不存在“摩擦力势能”的概念。
环节五:若某个力做功与路径有关还能否定义
相应的势能
课堂练习
BCD
课堂练习
BD
课堂练习
3.如图所示,质量为m的足球从地面上的位置1被踢出后落到地面上的位置3,在空中达到的最高点为位置2,且其高度为h。重力加速度为g。
(1)若选择地面作为零势能面,则足球在位置2的重力势能是多大 若选择最高点作为零势能面,则足球在位置3的重力势能是多大
(2)足球由位置1运动到位置2的过程中,重力做了多少功 足球的重力势能变化了多少
(3)足球由位置2运动到位置3的过程中,重力做了多少功 足球的重力势能变化了多少
(4)足球由位置1运动到位置3的过程中,重力做了多少功
(1)mgh ﹣mgh (2)﹣mgh mgh (3)mgh ﹣mgh (4)0
