第三章 图形的平移与旋转(单元小结)课件(共25张PPT)
文档属性
| 名称 | 第三章 图形的平移与旋转(单元小结)课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:47 | ||
图片预览




文档简介
(共25张PPT)
第三章
图形的平移与旋转
单元小结
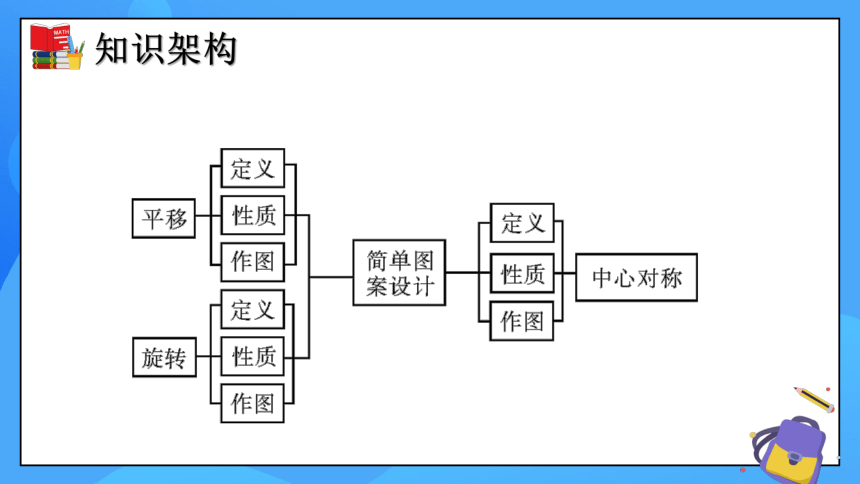
本章知识架构
知识专题
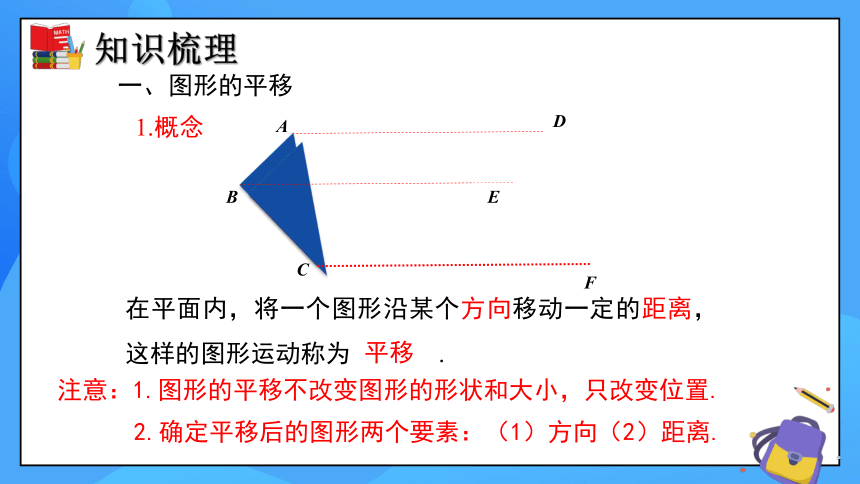
一、图形的平移
1.概念
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为 .
平移
注意:1.图形的平移不改变图形的形状和大小,只改变位置.
A
B
C
D
E
F
2.确定平移后的图形两个要素:(1)方向(2)距离.
知识专题
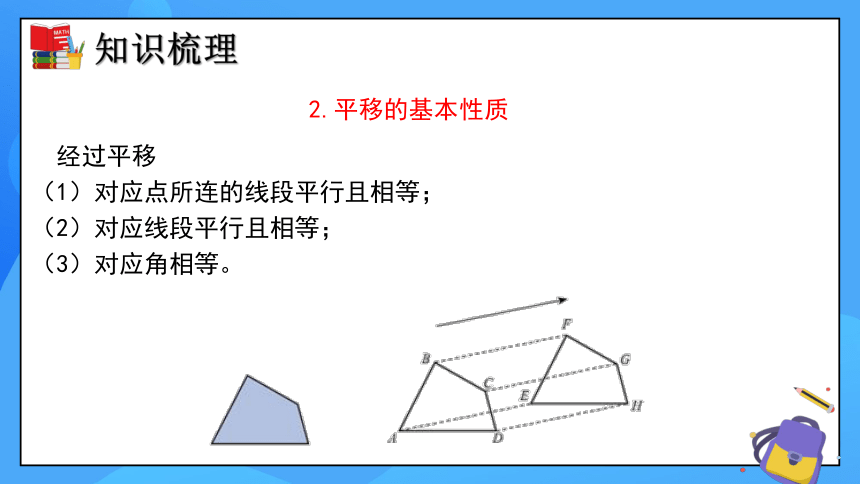
2.平移的基本性质
经过平移
(1)对应点所连的线段平行且相等;
(2)对应线段平行且相等;
(3)对应角相等。
知识专题
3.平移作图的一般步骤:
应分四步——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(平行和相等可以按照平移方向和距离,也可以按照对应边的关系)
(4)连:按原图顺次连接对应点.
知识专题
4.图形平移后,各点坐标的变化规律
如果平移的单位是常量a(a>0),原坐标为(x,y),图形平移后的对应点的坐标:
①原图形向右(向左)平移a个单位长度:对应点的坐标为(x±a,y)
②原图形向上(向下)平移a个单位长度:对应点的坐标为(x,y±a)
知识专题
5.坐标变化后,图形的变化规律
①横坐标保持不变,纵坐标分别加2,原图形被向上平移2个单位长度.
②横坐标保持不变,纵坐标分别减2,原图形被向下平移2个单位长度.
知识专题
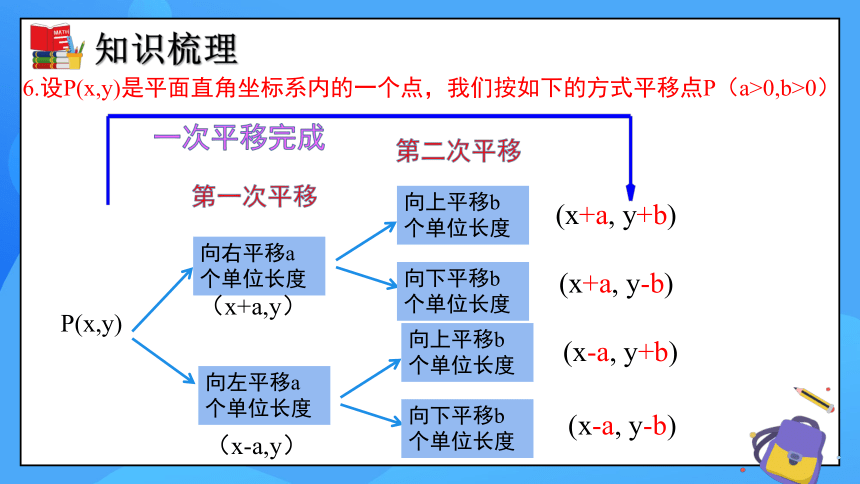
6.设P(x,y)是平面直角坐标系内的一个点,我们按如下的方式平移点P(a>0,b>0)
P(x,y)
(x+a, y+b)
(x+a, y-b)
(x-a, y+b)
(x-a, y-b)
向右平移a
个单位长度
向左平移a
个单位长度
第一次平移
向上平移b
个单位长度
向下平移b
个单位长度
向上平移b
个单位长度
向下平移b
个单位长度
第二次平移
一次平移完成
(x+a,y)
(x-a,y)
知识专题
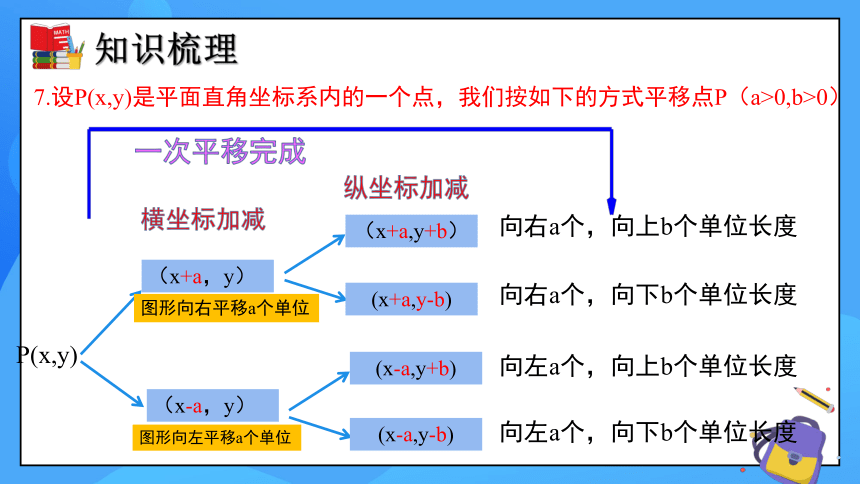
7.设P(x,y)是平面直角坐标系内的一个点,我们按如下的方式平移点P(a>0,b>0)
P(x,y)
(x+a,y)
(x-a,y)
横坐标加减
(x+a,y+b)
(x+a,y-b)
(x-a,y+b)
(x-a,y-b)
纵坐标加减
向右a个,向上b个单位长度
向右a个,向下b个单位长度
向左a个,向上b个单位长度
向左a个,向下b个单位长度
一次平移完成
图形向右平移a个单位
图形向左平移a个单位
知识专题
原图形上点P(x,y)
平移后图形上点P(x±a,y±b)
图形沿x轴方向平移a个单位长度
图形沿y轴方向平移b个单位长度
平移的方向:从原图形上一点到其对应点的方向.
平移的距离:
将一个图形沿着x轴方向平移a(a>0)个单位长度;再严重y轴方向平移b个单位长度,平移前后图形对应点的坐标关系
二、图形的旋转
1.概念
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称旋转.这个定点称为旋转中心,转动的角称为旋转角。
知识专题
旋转中心
旋转角
旋转方向
确定一次图形的旋转时,必须明确
温馨提示:①旋转的范围是“平面内”;
②旋转变换同样属于全等变换.
旋转三要素
旋转不改变图形的形状和大小
旋转角:是对应点与旋转中心所连线段的夹角
知识专题
2.旋转的性质
(1)旋转不改变图形的大小和形状.
(2)对应线段相等,对应角相等.
(3)对应点到旋转中心的距离相等.
(4)任意一组对应点与旋转中心的连线所成的角都等于旋转角.
知识专题
(1)确定旋转中心、旋转方向和旋转角;
(2)将图形中的关键点与旋转中心连接起来,然后按旋转方向分别将它们旋转旋转角,截取相等线段得到关键点的对应点;
(3)按照原图形的顺序连接这些对应点,所得到的图形就是旋转后的图形;
(4)写出结论。
3.画旋转图形的一般步骤:
知识专题
三、中心对称
1.概念
中心对称:如果把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心.
中心对称的特征:
①两个图形能够完全重合;
②重合方式有限制:绕着某一点旋转180°.
中心对称本质上是一种特殊的旋转
知识专题
(1)成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.(即对称点与对称中心三点共线)
(2)中心对称的两个图形是全等形.
2.中心对称的性质
知识专题
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
3.中心对称图形
中心对称图形是指一个图形.
注意:
知识专题
4.中心对称与中心对称图形的区别与联系:
中心对称 中心对称图形
区别 (1)是针对2个图形而言的 (2)是指两个图形的(位置)关系 (3)对称点在两个图形上 (4)对称中心在两个图形之间 (1)是针对1个图形而言的
(2)是指具有某种性质的一个图形
(3)对称点在一个图形上
(4)对称中心在图形上或其内部
联系 若把成中心对称的两个图形视为一个整体,则成为中心对称图形;若把中心对称图形的两部分看作两个图形,则它们成中心对称
知识专题
考点专练
考点一 平移
1.如图所示,△DEF经过平移得到△ABC,那么∠C的对应角和ED的对应边分别是 ( )
A.∠F,AC
B.∠BOD,BA
C.∠F,BA
D.∠BOD,AC
C
平移前后的图形形状和大小完全相同,任何一对对应点连线段平行(或共线)且相等.
考点专练
考点二 坐标系中的图形平移
2.如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6,b+2),
(1)请画出上述平移后的△A1B1C1,
并写出点A、C、A1、C1的坐标;
(2)求出以A、C、A1、C1为顶
点的四边形的面积.
考点专练
解:(1)△A1B1C1如图所示;各点的坐标为:A (﹣3,2)、C(﹣2,0)、A1(3,4)、C1(4,2);
(2)如图,连接AA1、CC1;△AC1C的面积
△AC1A1的面积
四边形ACC1A1的面积为7+7=14.
答:四边形ACC1A1的面积为14.
考点专练
考点三 旋转的概念及性质的应用
3.如图,在等腰Rt△ABC中,点O是AB的中点,AC=4, 将一块边长足够大的三角板的直角顶点放在O点处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为D,另一条直角边与BC相交,交点为E,则等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD
与CE长度之和等于 .
A
B
C
D
E
O
4
考点专练
考点四 中心对称
4.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为_______.
解析:由于矩形是中心对称图形,所以依题意可知△BOF与△DOE关于点O成中心对称,由此图中阴影部分的三个三角形就可以转化到直角△ADC中,易得阴影部分的面积为3.
3
复习题
第2、5、7、9题
第三章
图形的平移与旋转
单元小结
本章知识架构
知识专题
一、图形的平移
1.概念
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为 .
平移
注意:1.图形的平移不改变图形的形状和大小,只改变位置.
A
B
C
D
E
F
2.确定平移后的图形两个要素:(1)方向(2)距离.
知识专题
2.平移的基本性质
经过平移
(1)对应点所连的线段平行且相等;
(2)对应线段平行且相等;
(3)对应角相等。
知识专题
3.平移作图的一般步骤:
应分四步——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(平行和相等可以按照平移方向和距离,也可以按照对应边的关系)
(4)连:按原图顺次连接对应点.
知识专题
4.图形平移后,各点坐标的变化规律
如果平移的单位是常量a(a>0),原坐标为(x,y),图形平移后的对应点的坐标:
①原图形向右(向左)平移a个单位长度:对应点的坐标为(x±a,y)
②原图形向上(向下)平移a个单位长度:对应点的坐标为(x,y±a)
知识专题
5.坐标变化后,图形的变化规律
①横坐标保持不变,纵坐标分别加2,原图形被向上平移2个单位长度.
②横坐标保持不变,纵坐标分别减2,原图形被向下平移2个单位长度.
知识专题
6.设P(x,y)是平面直角坐标系内的一个点,我们按如下的方式平移点P(a>0,b>0)
P(x,y)
(x+a, y+b)
(x+a, y-b)
(x-a, y+b)
(x-a, y-b)
向右平移a
个单位长度
向左平移a
个单位长度
第一次平移
向上平移b
个单位长度
向下平移b
个单位长度
向上平移b
个单位长度
向下平移b
个单位长度
第二次平移
一次平移完成
(x+a,y)
(x-a,y)
知识专题
7.设P(x,y)是平面直角坐标系内的一个点,我们按如下的方式平移点P(a>0,b>0)
P(x,y)
(x+a,y)
(x-a,y)
横坐标加减
(x+a,y+b)
(x+a,y-b)
(x-a,y+b)
(x-a,y-b)
纵坐标加减
向右a个,向上b个单位长度
向右a个,向下b个单位长度
向左a个,向上b个单位长度
向左a个,向下b个单位长度
一次平移完成
图形向右平移a个单位
图形向左平移a个单位
知识专题
原图形上点P(x,y)
平移后图形上点P(x±a,y±b)
图形沿x轴方向平移a个单位长度
图形沿y轴方向平移b个单位长度
平移的方向:从原图形上一点到其对应点的方向.
平移的距离:
将一个图形沿着x轴方向平移a(a>0)个单位长度;再严重y轴方向平移b个单位长度,平移前后图形对应点的坐标关系
二、图形的旋转
1.概念
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称旋转.这个定点称为旋转中心,转动的角称为旋转角。
知识专题
旋转中心
旋转角
旋转方向
确定一次图形的旋转时,必须明确
温馨提示:①旋转的范围是“平面内”;
②旋转变换同样属于全等变换.
旋转三要素
旋转不改变图形的形状和大小
旋转角:是对应点与旋转中心所连线段的夹角
知识专题
2.旋转的性质
(1)旋转不改变图形的大小和形状.
(2)对应线段相等,对应角相等.
(3)对应点到旋转中心的距离相等.
(4)任意一组对应点与旋转中心的连线所成的角都等于旋转角.
知识专题
(1)确定旋转中心、旋转方向和旋转角;
(2)将图形中的关键点与旋转中心连接起来,然后按旋转方向分别将它们旋转旋转角,截取相等线段得到关键点的对应点;
(3)按照原图形的顺序连接这些对应点,所得到的图形就是旋转后的图形;
(4)写出结论。
3.画旋转图形的一般步骤:
知识专题
三、中心对称
1.概念
中心对称:如果把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心.
中心对称的特征:
①两个图形能够完全重合;
②重合方式有限制:绕着某一点旋转180°.
中心对称本质上是一种特殊的旋转
知识专题
(1)成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.(即对称点与对称中心三点共线)
(2)中心对称的两个图形是全等形.
2.中心对称的性质
知识专题
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
3.中心对称图形
中心对称图形是指一个图形.
注意:
知识专题
4.中心对称与中心对称图形的区别与联系:
中心对称 中心对称图形
区别 (1)是针对2个图形而言的 (2)是指两个图形的(位置)关系 (3)对称点在两个图形上 (4)对称中心在两个图形之间 (1)是针对1个图形而言的
(2)是指具有某种性质的一个图形
(3)对称点在一个图形上
(4)对称中心在图形上或其内部
联系 若把成中心对称的两个图形视为一个整体,则成为中心对称图形;若把中心对称图形的两部分看作两个图形,则它们成中心对称
知识专题
考点专练
考点一 平移
1.如图所示,△DEF经过平移得到△ABC,那么∠C的对应角和ED的对应边分别是 ( )
A.∠F,AC
B.∠BOD,BA
C.∠F,BA
D.∠BOD,AC
C
平移前后的图形形状和大小完全相同,任何一对对应点连线段平行(或共线)且相等.
考点专练
考点二 坐标系中的图形平移
2.如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6,b+2),
(1)请画出上述平移后的△A1B1C1,
并写出点A、C、A1、C1的坐标;
(2)求出以A、C、A1、C1为顶
点的四边形的面积.
考点专练
解:(1)△A1B1C1如图所示;各点的坐标为:A (﹣3,2)、C(﹣2,0)、A1(3,4)、C1(4,2);
(2)如图,连接AA1、CC1;△AC1C的面积
△AC1A1的面积
四边形ACC1A1的面积为7+7=14.
答:四边形ACC1A1的面积为14.
考点专练
考点三 旋转的概念及性质的应用
3.如图,在等腰Rt△ABC中,点O是AB的中点,AC=4, 将一块边长足够大的三角板的直角顶点放在O点处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为D,另一条直角边与BC相交,交点为E,则等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD
与CE长度之和等于 .
A
B
C
D
E
O
4
考点专练
考点四 中心对称
4.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为_______.
解析:由于矩形是中心对称图形,所以依题意可知△BOF与△DOE关于点O成中心对称,由此图中阴影部分的三个三角形就可以转化到直角△ADC中,易得阴影部分的面积为3.
3
复习题
第2、5、7、9题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
