第六章 平行四边形(单元小结)课件(共21张PPT)
文档属性
| 名称 | 第六章 平行四边形(单元小结)课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:47 | ||
图片预览




文档简介
(共21张PPT)
第六章 平行四边形
单元小结
本章知识架构
知识专题
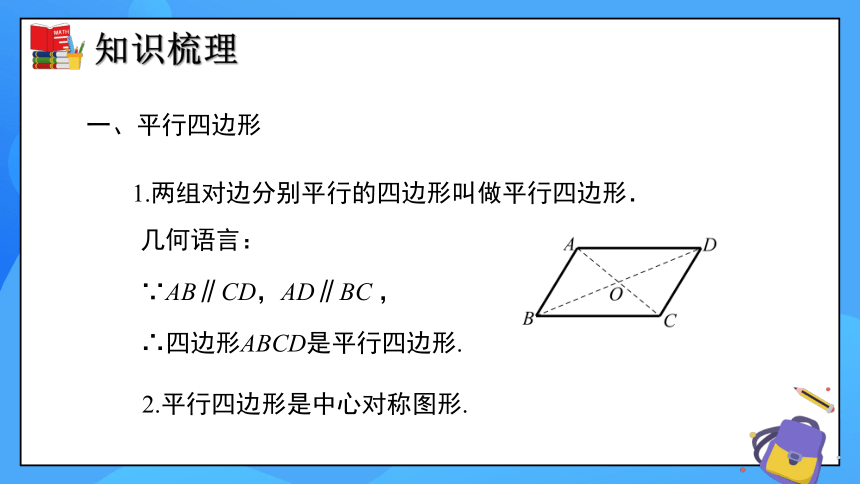
一、平行四边形
1.两组对边分别平行的四边形叫做平行四边形.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
2.平行四边形是中心对称图形.
知识专题
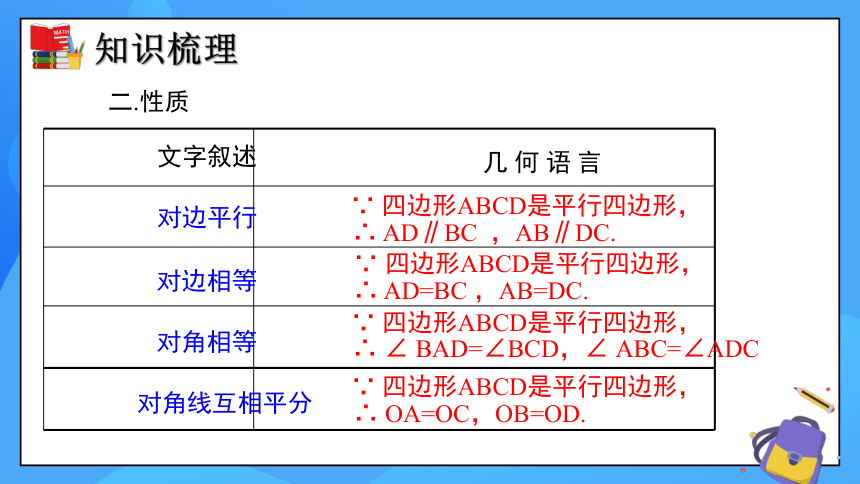
二.性质
几 何 语 言
文字叙述
对边平行
对边相等
对角相等
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ BAD=∠BCD,∠ ABC=∠ADC
∵ 四边形ABCD是平行四边形,
对角线互相平分
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
知识专题
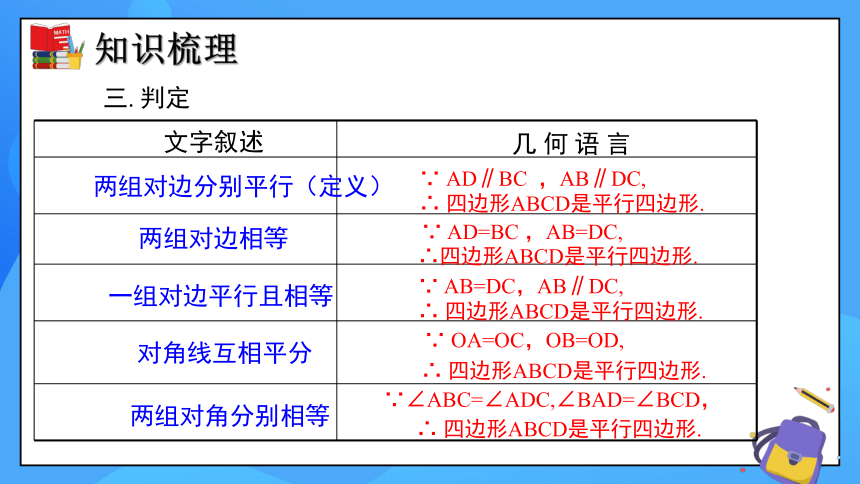
三. 判定
几 何 语 言
文字叙述
两组对边相等
一组对边平行且相等
∴四边形ABCD是平行四边形.
∵ AD=BC ,AB=DC,
∴ 四边形ABCD是平行四边形.
∵ AB=DC,AB∥DC,
对角线互相平分
∴ 四边形ABCD是平行四边形.
∵ OA=OC,OB=OD,
两组对边分别平行(定义)
∴ 四边形ABCD是平行四边形.
∵ AD∥BC ,AB∥DC,
两组对角分别相等
∵∠ABC=∠ADC,∠BAD=∠BCD,
∴ 四边形ABCD是平行四边形.
知识专题
2.定理:平行线间的距离相等
3.定理:夹在两条平行线间的平行线段相等
∟
∟
四.平行线间的距离
1.定义:如果两条直线互相平行,则其中一条直线上的任意一点到另一条直线的距离相等,这个距离称为平行线之间的距离.
知识专题
五.三角形中位线
2.定理:三角形的中位线平行于第三边,并且等于第三边的一半.
D
A
B
C
E
∵DE是△ABC的中位线,
∴DE∥BC,
3.用途:①证明平行问题
②证明一条线段是另一条线段的2倍或1/2
1.定义:连接三角形两边中点的线段叫做三角形的中位线
知识专题
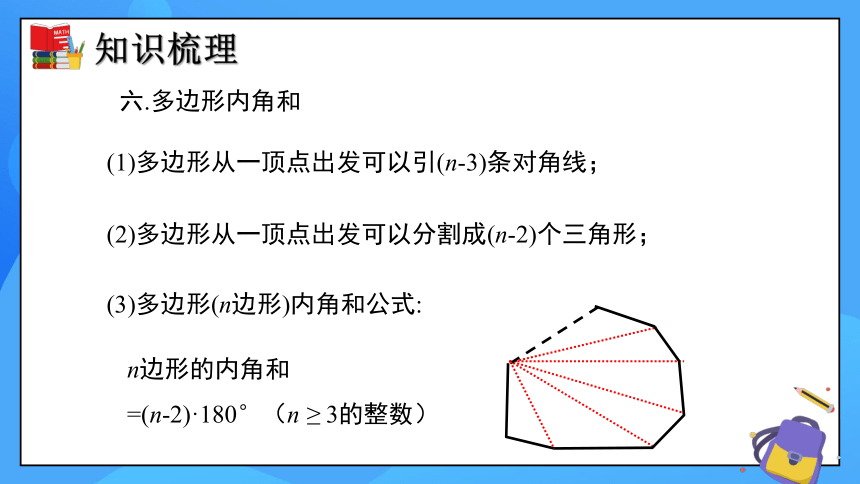
(3)多边形(n边形)内角和公式:
六.多边形内角和
n边形的内角和
=(n-2)·180°(n ≥ 3的整数)
(1)多边形从一顶点出发可以引(n-3)条对角线;
(2)多边形从一顶点出发可以分割成(n-2)个三角形;
知识专题
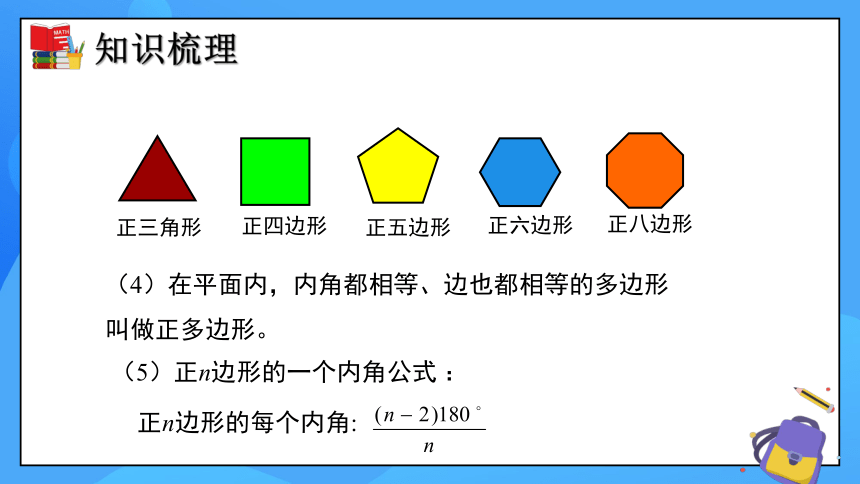
正三角形
正四边形
正五边形
正六边形
正八边形
(4)在平面内,内角都相等、边也都相等的多边形叫做正多边形。
(5)正n边形的一个内角公式 :
正n边形的每个内角:
知识专题
(1)定义:多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
An
A2
A3
A4
1
2
3
4
n
A1
七.多边形外角和
(3)多边形的外角和定理:
多边形的外角和都等于360°
(与边数无关)
(2)在多边形的每一个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和
考点专练
考点一:平行四边形的性质
1.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为( )
A. 8 B. 10 C. 12 D. 14
B
考点专练
2.如图,在 ABCD中,DE=BF,求证:AF=CE.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠ADF=∠CBE.
∵DE=BF,∴DF=BE.
在△ADF和△CBE中,
AD=CB,∠ADF=∠CBE,DE=BF,
∴△ADF≌△CBE(SAS).
∴AF=CE.
考点专练
考点二:平行四边形的判定
3.如图,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.
考点专练
证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°.
∵AB∥CD,∴∠A=∠D.
在△AEB和△DFC中,
∠AEB=∠DFC, AE=DF,∠A=∠D,
∴△AEB≌△DFC(ASA).
∴BE=CF.
∵BE⊥AD,CF⊥AD,
∴BE∥CF.
∴四边形BECF是平行四边形.
考点专练
考点三:三角形的中位线
4.如图,已知在△ABC中,D,E分别是AB,AC的中点,F,G分别是AD,AE的中点,且FG=2 cm,则BC的长度是______cm.
8
考点专练
5.如图, ABCD,点E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)过点D作DG⊥AE于点G,H为DG的中点,判断CH与DG的位置关系,并说明理由.
考点专练
(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD. ∴∠B=∠ECF.
∵E为BC的中点,∴BE=CE.
在△ABE和△FCE中,
∠B=∠ECF,BE=CE,∠AEB=∠FEC,
∴△ABE≌△FCE(ASA).
(2)解:CH⊥DG. 理由如下.
由(1)知△ABE≌△FCE,∴AB=CF.
∵AB=CD,∴DC=CF.
∵H为DG的中点,∴CH∥FG.
∵DG⊥AE,∴CH⊥DG.
考点专练
考点四:多边形内角和与外角和
6. 如图,∠1是五边形ABCDE的一个外角,若∠1=65°,则∠A+∠B+∠C+∠D=________.
425°
考点专练
7. 如图,某人从点A出发,前进8 m后向右转60°,再前进8 m后又向右转60°,按照这样的方式一直走下去,当他第一次回到出发点A时,共走了( )
A. 24 m B. 32 m
C. 40 m D. 48 m
D
复习题
第3、5、6、9、11、13、14题
第六章 平行四边形
单元小结
本章知识架构
知识专题
一、平行四边形
1.两组对边分别平行的四边形叫做平行四边形.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
2.平行四边形是中心对称图形.
知识专题
二.性质
几 何 语 言
文字叙述
对边平行
对边相等
对角相等
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ BAD=∠BCD,∠ ABC=∠ADC
∵ 四边形ABCD是平行四边形,
对角线互相平分
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
知识专题
三. 判定
几 何 语 言
文字叙述
两组对边相等
一组对边平行且相等
∴四边形ABCD是平行四边形.
∵ AD=BC ,AB=DC,
∴ 四边形ABCD是平行四边形.
∵ AB=DC,AB∥DC,
对角线互相平分
∴ 四边形ABCD是平行四边形.
∵ OA=OC,OB=OD,
两组对边分别平行(定义)
∴ 四边形ABCD是平行四边形.
∵ AD∥BC ,AB∥DC,
两组对角分别相等
∵∠ABC=∠ADC,∠BAD=∠BCD,
∴ 四边形ABCD是平行四边形.
知识专题
2.定理:平行线间的距离相等
3.定理:夹在两条平行线间的平行线段相等
∟
∟
四.平行线间的距离
1.定义:如果两条直线互相平行,则其中一条直线上的任意一点到另一条直线的距离相等,这个距离称为平行线之间的距离.
知识专题
五.三角形中位线
2.定理:三角形的中位线平行于第三边,并且等于第三边的一半.
D
A
B
C
E
∵DE是△ABC的中位线,
∴DE∥BC,
3.用途:①证明平行问题
②证明一条线段是另一条线段的2倍或1/2
1.定义:连接三角形两边中点的线段叫做三角形的中位线
知识专题
(3)多边形(n边形)内角和公式:
六.多边形内角和
n边形的内角和
=(n-2)·180°(n ≥ 3的整数)
(1)多边形从一顶点出发可以引(n-3)条对角线;
(2)多边形从一顶点出发可以分割成(n-2)个三角形;
知识专题
正三角形
正四边形
正五边形
正六边形
正八边形
(4)在平面内,内角都相等、边也都相等的多边形叫做正多边形。
(5)正n边形的一个内角公式 :
正n边形的每个内角:
知识专题
(1)定义:多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
An
A2
A3
A4
1
2
3
4
n
A1
七.多边形外角和
(3)多边形的外角和定理:
多边形的外角和都等于360°
(与边数无关)
(2)在多边形的每一个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和
考点专练
考点一:平行四边形的性质
1.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为( )
A. 8 B. 10 C. 12 D. 14
B
考点专练
2.如图,在 ABCD中,DE=BF,求证:AF=CE.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠ADF=∠CBE.
∵DE=BF,∴DF=BE.
在△ADF和△CBE中,
AD=CB,∠ADF=∠CBE,DE=BF,
∴△ADF≌△CBE(SAS).
∴AF=CE.
考点专练
考点二:平行四边形的判定
3.如图,已知AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.
考点专练
证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°.
∵AB∥CD,∴∠A=∠D.
在△AEB和△DFC中,
∠AEB=∠DFC, AE=DF,∠A=∠D,
∴△AEB≌△DFC(ASA).
∴BE=CF.
∵BE⊥AD,CF⊥AD,
∴BE∥CF.
∴四边形BECF是平行四边形.
考点专练
考点三:三角形的中位线
4.如图,已知在△ABC中,D,E分别是AB,AC的中点,F,G分别是AD,AE的中点,且FG=2 cm,则BC的长度是______cm.
8
考点专练
5.如图, ABCD,点E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)过点D作DG⊥AE于点G,H为DG的中点,判断CH与DG的位置关系,并说明理由.
考点专练
(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD. ∴∠B=∠ECF.
∵E为BC的中点,∴BE=CE.
在△ABE和△FCE中,
∠B=∠ECF,BE=CE,∠AEB=∠FEC,
∴△ABE≌△FCE(ASA).
(2)解:CH⊥DG. 理由如下.
由(1)知△ABE≌△FCE,∴AB=CF.
∵AB=CD,∴DC=CF.
∵H为DG的中点,∴CH∥FG.
∵DG⊥AE,∴CH⊥DG.
考点专练
考点四:多边形内角和与外角和
6. 如图,∠1是五边形ABCDE的一个外角,若∠1=65°,则∠A+∠B+∠C+∠D=________.
425°
考点专练
7. 如图,某人从点A出发,前进8 m后向右转60°,再前进8 m后又向右转60°,按照这样的方式一直走下去,当他第一次回到出发点A时,共走了( )
A. 24 m B. 32 m
C. 40 m D. 48 m
D
复习题
第3、5、6、9、11、13、14题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
