专题04:圆-2023-2024学年六年级上册数学期末核心考点集训课件 人教版(共25张PPT)
文档属性
| 名称 | 专题04:圆-2023-2024学年六年级上册数学期末核心考点集训课件 人教版(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 21:42:43 | ||
图片预览







文档简介
(共25张PPT)
圆
复习专题
人教版六年级数学上册
圆的认识
1
圆的周长
2
圆的面积
3
扇形
4
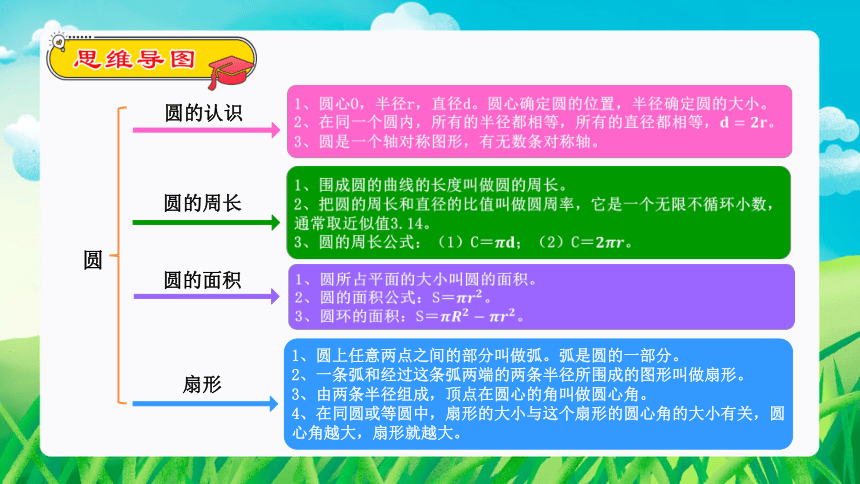
圆
1、围成圆的曲线的长度叫做圆的周长。
2、把圆的周长和直径的比值叫做圆周率,它是一个无限不循环小数,通常取近似值3.14。
3、圆的周长公式:(1)C=;(2)C=。
1、圆所占平面的大小叫圆的面积。
2、圆的面积公式:S=。
3、圆环的面积:S=。
圆的认识
圆的周长
圆的面积
1、圆心O,半径r,直径d。圆心确定圆的位置,半径确定圆的大小。
2、在同一个圆内,所有的半径都相等,所有的直径都相等,。
3、圆是一个轴对称图形,有无数条对称轴。
1、圆上任意两点之间的部分叫做弧。弧是圆的一部分。
2、一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
3、由两条半径组成,顶点在圆心的角叫做圆心角。
4、在同圆或等圆中,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形就越大。
扇形
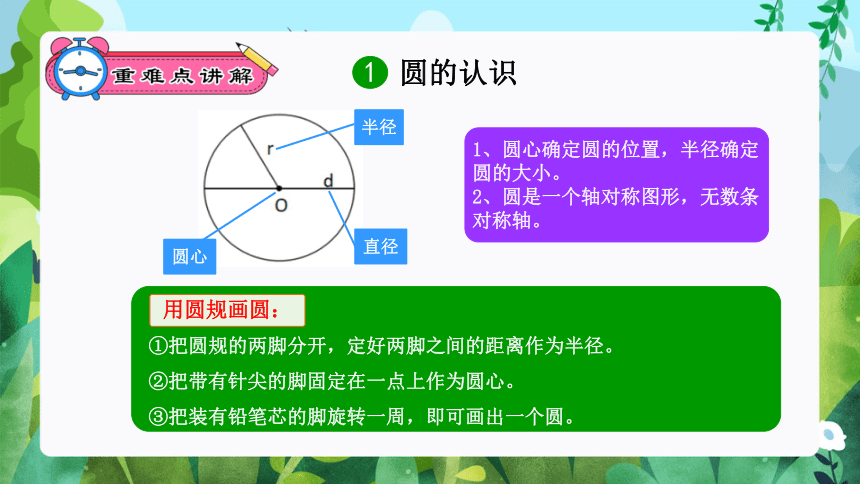
①把圆规的两脚分开,定好两脚之间的距离作为半径。
②把带有针尖的脚固定在一点上作为圆心。
③把装有铅笔芯的脚旋转一周,即可画出一个圆。
用圆规画圆:
圆的认识
1
圆心
半径
直径
1、圆心确定圆的位置,半径确定圆的大小。
2、圆是一个轴对称图形,无数条对称轴。
【例1】第十九届亚洲运动会于2023年9月23日晚在浙江省杭州市隆重开幕。杭州亚运会的金牌的直径为8厘米,那么它的半径是( )厘米。
A、8 B、6 C、4 D、2
C
1、在同一个圆内,所有的半径都相等,所有的直径都相等。
2、直径是半径的两倍,用字母表示是: 或
圆的特征:
1、下列说法中,正确的是( )。
A、篮球是一个圆。
B、一个圆有1条对称轴。
C、直径是圆中最长的一条直线。
D、把一个半圆沿着直径所在的直线作轴对称图形可以得到一个整圆。
D
球
无数条
线段
圆的周长
2
【例2】荷兰是一个拥有丰富历史和文化的国家,风车是荷兰的标志性建筑之一。一座荷兰风车的一片叶片长12米,那么这片风车叶片旋转一周叶片顶端扫过多少米?
1、围成圆的曲线的长度叫做圆的周长。
2、圆的周长公式:
(1)C= ;
(2)C= 。
3、一般在计算时π取3.14。
圆的周长:
【分析】风车叶片的长度就是圆的半径。
圆的周长=半径×3.14×2。
12×3.14×2
=37.68×2
=75.36(米)
答:这片风车叶片旋转一周叶片顶端扫过75.36米。
【例3】何阿姨用一根麻绳绕着一根直径是18分米的树干绕了5圈,还剩下6分米,这根麻绳长多少分米?
【分析】麻绳的长度=直径×3.14×5圈+剩下的长度。
18×3.14×5+6
=56.52×5+6
=282.6+6
=288.6(分米)
答:这根麻绳长288.6分米。
C=
圆的周长公式:
1、有一台压路机的振动滚筒的半径是0.6米,如果这个振动滚筒每分转5周,那么它每小时能前进多少米?
【分析】振动滚筒滚动一周的路程=半径×2×3.14
总路程=振动滚筒滚动一周的路程×每分转5周×60分钟
0.6×2×3.14
=1.2×3.14
=3.768(米)
3.768×5×60
=18.84×60
=1130.4(米)
答:它每小时能前进1130.4米。
【例4】如图,学校有一条环形跑道。
(1)请你求一求这条是多少米?
(2)刘小胖跑步的速度是每秒2米,他绕着环形
跑道最外围的一圈跑道跑完一圈要多少分钟?
【分析】(1)环形跑道的周长=直径×3.14+143×2
(1)100×3.14+143×2
=314+286
=600(米)
答:这条环形跑道的周长是600米。
【例4】如图,学校有一条环形跑道。
(1)请你求一求这条是多少米?
(2)刘小胖跑步的速度是每秒2米,他绕着环形
跑道最外围的一圈跑道跑完一圈要多少分钟?
【分析】(2)时间=路程÷速度
(2)600÷2=300(秒)
300秒=5分钟
答:他跑完一圈要5分钟。
1、计算下面图形的周长。
【分析】图形周长=小圆的周长+大圆周长的一半
8×3.14=25.12(厘米)
8×3.14×2÷2=25.12(厘米)
25.12+25.12=50.24(厘米)
圆的面积
3
【例5】有一个圆形的蓄水池,它的直径是12米,这个蓄水池的占地面积是多少平方米?
1、圆所占平面的大小叫圆的面积。
2、圆的面积公式: S=。
3、一般在计算时π取3.14。
圆的面积:
【分析】圆的半径=圆的直径÷2;
圆的面积=半径的平方×3.14。
12÷2=6(米)
×3.14
=36×3.14
=113.04(平方米)
答:这个蓄水池的占地面积是113.04平方米。
1、墙上挂着一只时钟,它的分针长0.9分米,经过30分钟后,这根分针扫过的面积是多少平方分米?(得数保留一位小数。)
×3.14÷2
=0.81×3.14÷2
=2.5434÷2
=1.2717
≈1.3(平方分米)
【分析】经过30分钟分针所扫过的区域面积就是半个圆的面积;
所求的面积=半径的平方×3.14÷2。
答:这根分针的扫过的面积是1.3平方分米。
【例6】已知一个长方形的长是19.8分米,宽是11.6分米,这个长方形的周长与一个圆的周长相等,这个圆的面积是多少平方分米?
(19.8+11.6)×2
=31.4×2
=62.8(分米)
【分析】长方形的周长(即圆的周长)=(长方形的长+长方形的宽)×2;
圆的半径=圆的周长÷2÷3.14;
圆的面积=半径的平方×3.14。
62.8÷3.14÷2
=20÷2
=10(分米)
×3.14
=100×3.14
=314(平方分米)
答:这个圆的面积是314平方分米。
【例7】在一张边长是10厘米的正方形纸片中画一个最大的圆,这个圆的面积是多少平方厘米?
正方形的边长即为这个最大的圆的直径。
这个正方形的对角线的长度即为圆的直径。
在正方形内画一个最大的圆:
【分析】 圆的面积=半径的平方×3.14。
×3.14
×3.14
=25×3.14
=78.5(平方厘米)
答:这个圆的面积是78.5平方厘米。
在圆内画一个最大的正方形:
【例8】市民广场修建了一个半径是7米圆形景观池,现在要在景观池的外围修一条2米宽的环形石子路,这条环形石子路的面积是多少平方米?
【分析】大圆的半径=小圆半径+2;
环形石子路的面积=大圆的面积-小圆的面积。
7+2=9(米)
×3.14- ×3.14
=81×3.14-49×3.14
=254.34-153.86
=100.48(平方米)
S=
圆环面积公式:
答:这条环形石子路的面积是100.48平方米。
扇形
4
1、圆上任意两点之间的部分叫做弧。弧是圆的一部分。
2、一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
3、由两条半径组成,顶点在圆心的角叫做圆心角。
4、在同圆或等圆中,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形就越大。
扇形:
A
B
弧
圆心角
扇形
【例9】在一个半径是3厘米的圆中有一个圆心角为90°的扇形,这个扇形的面积是( )平方厘米 。
7.065
【分析】圆的面积=半径的平方×3.14;
圆心角为90°的扇形的面积=×圆的面积
×3.14×
=9×3.14×
=28.26×
=7.065(平方厘米)
1、判断题。(对的在括号里打“√”,错的打“×”)
(1)用一张边长为12厘米的正方形卡纸剪出四个同样的最大的圆,圆的直径是6厘米。( )
(2)两个圆一定可以拼成一个圆环。( )
(3)如果大圆的半径是小圆半径的2倍,那么大圆面积是小圆面积的4倍( )。
(4)如果两个圆的半径相等,则它们的面积不一定相等。( )
(5)一个半圆的面积就等于这个圆面积的一半。( )
(6)将一个圆的半径缩小,这个圆的面积就缩小了。( )
√
×
√
×
√
√
2、将一个圆对折两次,可以得到这个圆的( )。
A、周长 B、直径 C、圆心 D、面积
3、李玲用圆规要画一个直径为6.8厘米的圆,圆规两脚间的距离应该是( )厘米。
4、如果两个圆的半径的比是7∶5,那么这两个圆的周长比是( ),面积比的( )。
6.8÷2=3.4(厘米)
3.4
7∶5
49∶25
C
5、刘丁丁想在一张长为18厘米、宽为14厘米的长方形纸内画一个最大的圆,那么这个圆的半径是( )厘米。
6、如果把一个周长是125.6厘米的圆平均分成两个半圆,那么每个半圆的周长是( )厘米。
125.6÷3.14=40(厘米)
40+125.6÷2
=40+62.8
=102.8(厘米)
7
102.8
14÷2=7(厘米)
7、工程队挖了一个直径是3米的圆形坑来修补道路下方破损的排水管,现在要沿着这个圆形坑的边线拉一圈警示线,这圈警示线长多少米?
3×3.14=9.42(米)
答:这圈警示线长9.42米。
8、何叔叔需要一些直径是8厘米的圆形铁片,他在一张长是6分米、宽是5.4分米的长方形铁片上,最多能剪多少个的这样的圆形铁片?
8厘米=0.8分米
6÷0.8≈7(个)
5.4÷0.8≈6(个)
6×7=42(个)
答:最多能剪42个的这样的圆形铁片。
每一份努力,都将在学习中得到最好的回报。加油!
圆
复习专题
人教版六年级数学上册
圆的认识
1
圆的周长
2
圆的面积
3
扇形
4
圆
1、围成圆的曲线的长度叫做圆的周长。
2、把圆的周长和直径的比值叫做圆周率,它是一个无限不循环小数,通常取近似值3.14。
3、圆的周长公式:(1)C=;(2)C=。
1、圆所占平面的大小叫圆的面积。
2、圆的面积公式:S=。
3、圆环的面积:S=。
圆的认识
圆的周长
圆的面积
1、圆心O,半径r,直径d。圆心确定圆的位置,半径确定圆的大小。
2、在同一个圆内,所有的半径都相等,所有的直径都相等,。
3、圆是一个轴对称图形,有无数条对称轴。
1、圆上任意两点之间的部分叫做弧。弧是圆的一部分。
2、一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
3、由两条半径组成,顶点在圆心的角叫做圆心角。
4、在同圆或等圆中,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形就越大。
扇形
①把圆规的两脚分开,定好两脚之间的距离作为半径。
②把带有针尖的脚固定在一点上作为圆心。
③把装有铅笔芯的脚旋转一周,即可画出一个圆。
用圆规画圆:
圆的认识
1
圆心
半径
直径
1、圆心确定圆的位置,半径确定圆的大小。
2、圆是一个轴对称图形,无数条对称轴。
【例1】第十九届亚洲运动会于2023年9月23日晚在浙江省杭州市隆重开幕。杭州亚运会的金牌的直径为8厘米,那么它的半径是( )厘米。
A、8 B、6 C、4 D、2
C
1、在同一个圆内,所有的半径都相等,所有的直径都相等。
2、直径是半径的两倍,用字母表示是: 或
圆的特征:
1、下列说法中,正确的是( )。
A、篮球是一个圆。
B、一个圆有1条对称轴。
C、直径是圆中最长的一条直线。
D、把一个半圆沿着直径所在的直线作轴对称图形可以得到一个整圆。
D
球
无数条
线段
圆的周长
2
【例2】荷兰是一个拥有丰富历史和文化的国家,风车是荷兰的标志性建筑之一。一座荷兰风车的一片叶片长12米,那么这片风车叶片旋转一周叶片顶端扫过多少米?
1、围成圆的曲线的长度叫做圆的周长。
2、圆的周长公式:
(1)C= ;
(2)C= 。
3、一般在计算时π取3.14。
圆的周长:
【分析】风车叶片的长度就是圆的半径。
圆的周长=半径×3.14×2。
12×3.14×2
=37.68×2
=75.36(米)
答:这片风车叶片旋转一周叶片顶端扫过75.36米。
【例3】何阿姨用一根麻绳绕着一根直径是18分米的树干绕了5圈,还剩下6分米,这根麻绳长多少分米?
【分析】麻绳的长度=直径×3.14×5圈+剩下的长度。
18×3.14×5+6
=56.52×5+6
=282.6+6
=288.6(分米)
答:这根麻绳长288.6分米。
C=
圆的周长公式:
1、有一台压路机的振动滚筒的半径是0.6米,如果这个振动滚筒每分转5周,那么它每小时能前进多少米?
【分析】振动滚筒滚动一周的路程=半径×2×3.14
总路程=振动滚筒滚动一周的路程×每分转5周×60分钟
0.6×2×3.14
=1.2×3.14
=3.768(米)
3.768×5×60
=18.84×60
=1130.4(米)
答:它每小时能前进1130.4米。
【例4】如图,学校有一条环形跑道。
(1)请你求一求这条是多少米?
(2)刘小胖跑步的速度是每秒2米,他绕着环形
跑道最外围的一圈跑道跑完一圈要多少分钟?
【分析】(1)环形跑道的周长=直径×3.14+143×2
(1)100×3.14+143×2
=314+286
=600(米)
答:这条环形跑道的周长是600米。
【例4】如图,学校有一条环形跑道。
(1)请你求一求这条是多少米?
(2)刘小胖跑步的速度是每秒2米,他绕着环形
跑道最外围的一圈跑道跑完一圈要多少分钟?
【分析】(2)时间=路程÷速度
(2)600÷2=300(秒)
300秒=5分钟
答:他跑完一圈要5分钟。
1、计算下面图形的周长。
【分析】图形周长=小圆的周长+大圆周长的一半
8×3.14=25.12(厘米)
8×3.14×2÷2=25.12(厘米)
25.12+25.12=50.24(厘米)
圆的面积
3
【例5】有一个圆形的蓄水池,它的直径是12米,这个蓄水池的占地面积是多少平方米?
1、圆所占平面的大小叫圆的面积。
2、圆的面积公式: S=。
3、一般在计算时π取3.14。
圆的面积:
【分析】圆的半径=圆的直径÷2;
圆的面积=半径的平方×3.14。
12÷2=6(米)
×3.14
=36×3.14
=113.04(平方米)
答:这个蓄水池的占地面积是113.04平方米。
1、墙上挂着一只时钟,它的分针长0.9分米,经过30分钟后,这根分针扫过的面积是多少平方分米?(得数保留一位小数。)
×3.14÷2
=0.81×3.14÷2
=2.5434÷2
=1.2717
≈1.3(平方分米)
【分析】经过30分钟分针所扫过的区域面积就是半个圆的面积;
所求的面积=半径的平方×3.14÷2。
答:这根分针的扫过的面积是1.3平方分米。
【例6】已知一个长方形的长是19.8分米,宽是11.6分米,这个长方形的周长与一个圆的周长相等,这个圆的面积是多少平方分米?
(19.8+11.6)×2
=31.4×2
=62.8(分米)
【分析】长方形的周长(即圆的周长)=(长方形的长+长方形的宽)×2;
圆的半径=圆的周长÷2÷3.14;
圆的面积=半径的平方×3.14。
62.8÷3.14÷2
=20÷2
=10(分米)
×3.14
=100×3.14
=314(平方分米)
答:这个圆的面积是314平方分米。
【例7】在一张边长是10厘米的正方形纸片中画一个最大的圆,这个圆的面积是多少平方厘米?
正方形的边长即为这个最大的圆的直径。
这个正方形的对角线的长度即为圆的直径。
在正方形内画一个最大的圆:
【分析】 圆的面积=半径的平方×3.14。
×3.14
×3.14
=25×3.14
=78.5(平方厘米)
答:这个圆的面积是78.5平方厘米。
在圆内画一个最大的正方形:
【例8】市民广场修建了一个半径是7米圆形景观池,现在要在景观池的外围修一条2米宽的环形石子路,这条环形石子路的面积是多少平方米?
【分析】大圆的半径=小圆半径+2;
环形石子路的面积=大圆的面积-小圆的面积。
7+2=9(米)
×3.14- ×3.14
=81×3.14-49×3.14
=254.34-153.86
=100.48(平方米)
S=
圆环面积公式:
答:这条环形石子路的面积是100.48平方米。
扇形
4
1、圆上任意两点之间的部分叫做弧。弧是圆的一部分。
2、一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
3、由两条半径组成,顶点在圆心的角叫做圆心角。
4、在同圆或等圆中,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形就越大。
扇形:
A
B
弧
圆心角
扇形
【例9】在一个半径是3厘米的圆中有一个圆心角为90°的扇形,这个扇形的面积是( )平方厘米 。
7.065
【分析】圆的面积=半径的平方×3.14;
圆心角为90°的扇形的面积=×圆的面积
×3.14×
=9×3.14×
=28.26×
=7.065(平方厘米)
1、判断题。(对的在括号里打“√”,错的打“×”)
(1)用一张边长为12厘米的正方形卡纸剪出四个同样的最大的圆,圆的直径是6厘米。( )
(2)两个圆一定可以拼成一个圆环。( )
(3)如果大圆的半径是小圆半径的2倍,那么大圆面积是小圆面积的4倍( )。
(4)如果两个圆的半径相等,则它们的面积不一定相等。( )
(5)一个半圆的面积就等于这个圆面积的一半。( )
(6)将一个圆的半径缩小,这个圆的面积就缩小了。( )
√
×
√
×
√
√
2、将一个圆对折两次,可以得到这个圆的( )。
A、周长 B、直径 C、圆心 D、面积
3、李玲用圆规要画一个直径为6.8厘米的圆,圆规两脚间的距离应该是( )厘米。
4、如果两个圆的半径的比是7∶5,那么这两个圆的周长比是( ),面积比的( )。
6.8÷2=3.4(厘米)
3.4
7∶5
49∶25
C
5、刘丁丁想在一张长为18厘米、宽为14厘米的长方形纸内画一个最大的圆,那么这个圆的半径是( )厘米。
6、如果把一个周长是125.6厘米的圆平均分成两个半圆,那么每个半圆的周长是( )厘米。
125.6÷3.14=40(厘米)
40+125.6÷2
=40+62.8
=102.8(厘米)
7
102.8
14÷2=7(厘米)
7、工程队挖了一个直径是3米的圆形坑来修补道路下方破损的排水管,现在要沿着这个圆形坑的边线拉一圈警示线,这圈警示线长多少米?
3×3.14=9.42(米)
答:这圈警示线长9.42米。
8、何叔叔需要一些直径是8厘米的圆形铁片,他在一张长是6分米、宽是5.4分米的长方形铁片上,最多能剪多少个的这样的圆形铁片?
8厘米=0.8分米
6÷0.8≈7(个)
5.4÷0.8≈6(个)
6×7=42(个)
答:最多能剪42个的这样的圆形铁片。
每一份努力,都将在学习中得到最好的回报。加油!
