2.1.2 整式——单项式 课件(共18张PPT)
文档属性
| 名称 | 2.1.2 整式——单项式 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 450.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 09:17:52 | ||
图片预览






文档简介
(共18张PPT)
01情境导入
02问题导探
03典例导练
04小结导构
用含有字母的式子表示下列数量关系.
(1) 如果每年植树绿化x公顷荒山,那么这五
年内植树绿化荒山 公顷.
(2) 每本笔记本为m元,买六本笔记本需支付
元.
(3) 半径为r的圆的面积是 .
(4) 全校总人数是x,其中女生人数占了48%,
则女生人数是 .
5x
6m
0.48x
02问题导探
01情境导入
03典例导练
04小结导构
探究:观察下列所填代数式,它们有什么共同的特点吗?
5x
6m
0.48x
数字
字母
数字
字母
数字
字母
数字
字母
×
×
×
×
都是数与字母的乘积形式.
2.1.2 单项式
02问题导探
01情境导入
03典例导练
04小结导构
单项式的定义
只含有数与字母的积的式子叫做单项式.
注意:
单独的一个数或一个字母也是单项式.
比如: -3,0,m … …
02问题导探
01情境导入
03典例导练
04小结导构
判断下列各代数式是否是单项式?
⑤ ⑥
⑨ ⑩
圆周率 是常数
02问题导探
01情境导入
03典例导练
04小结导构
解剖单项式
单项式中的数字因数称为单项式的系数.
注意:单项式的系数要包括其前面的性质符号(正号可以省略,负号绝对不能落).
02问题导探
01情境导入
03典例导练
04小结导构
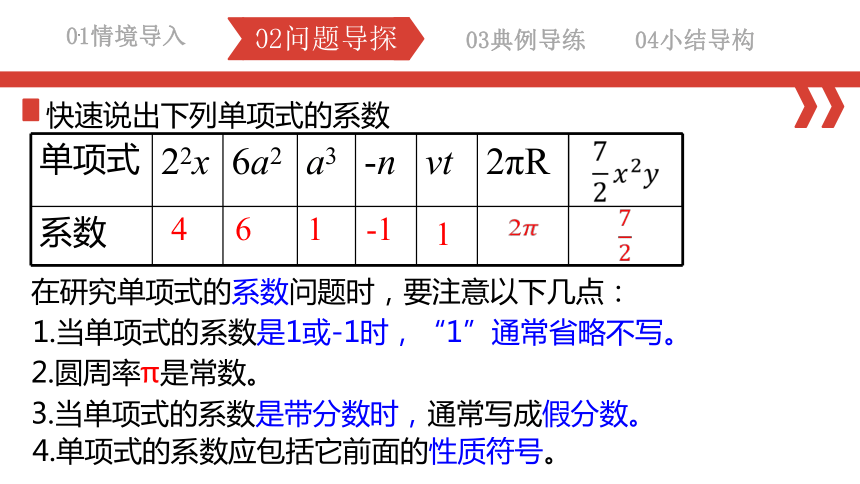
快速说出下列单项式的系数
单项式 22x 6a2 a3 -n vt 2πR
系数
4
在研究单项式的系数问题时,要注意以下几点:
1.当单项式的系数是1或-1时,“1”通常省略不写。
2.圆周率π是常数。
3.当单项式的系数是带分数时,通常写成假分数。
4.单项式的系数应包括它前面的性质符号。
6
1
-1
1
2
02问题导探
01情境导入
03典例导练
04小结导构
解剖单项式
所有字母指数的和称为单项式的次数
02问题导探
01情境导入
03典例导练
04小结导构
快速说出下列单项式的次数
单项式 22x 6a2 a3 -n vt 2πR
次数
1
在研究单项式的次数问题时,要注意以下几点:
1.在一个单项式中,所有字母的指数的和才叫做单项式的次数
2.单独一个数的次数记为0。
2
3
1
2
1
03典例导练
01情境导入
02问题导探
04小结导构
例1.用单项式填空,并指出它们的系数和次数.
1. 每包书有12册,n包书有_____册;
2. 底边长为a,高为h的三角形的面积是_____;
3. 一个长方体的长和宽都是a,高为h,它的体积是_____;
4. 一台电视机原价为a元,现按原价的九折出售,这台电视机 现在的售价为____;
5. 一个长方形的长为0.9,宽为a,面积是____.
12n
0.9a
0.9a
同一个式子可以表示不同的含义
12,一次
二次
1,三次
0.9,一次
0.9,一次
02问题导探
01情境导入
03典例导练
04小结导构
练习1.分别写出下列数的系数和次数:
你觉得找单项式的系数应注意什么?次数呢?
① ② ③
④ 1 ⑤ -1 ⑥ 0
03典例导练
01情境导入
02问题导探
04小结导构
练习2.判断,错误的地方请予以改正.
①-7xy2的系数是7;( )
②-x2y3与x3没有系数;( )
③-34ab3c2的次数是10;( )
④-a3的系数是-1; ( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是2( )
×
×
×
×
×
√
03典例导练
01情境导入
02问题导探
04小结导构
练习3.写出一个含有x、y,而且系数是-3,
次数是4的单项式.
x、y的指数之和为4即可
03典例导练
01情境导入
02问题导探
04小结导构
例2.
若是关于 x,y 的一个四次单项式,m,n应满足的条件?
即m≠ 2,n=2.
2+n=4,
m-2 ≠ 0
解:由题意得:
03典例导练
01情境导入
02问题导探
04小结导构
练习4.
若(-2)axby 与 的次数相同,系数的
整数部分相同,求正整数a、b的值.
03典例导练
01情境导入
02问题导探
04小结导构
当堂训练
1.下列各式是不是单项式?为什么?
2.判断下列各说法是否正确,将错误的改正过来.
(1)单项式 的系数是0, 次数是2. ( )
(2)单项式 的系数是2, 次数是10 . ( )
(3)单项式 的系数是 ,次数是n+1 . ( )
03典例导练
01情境导入
02问题导探
04小结导构
当堂训练
3.若a2x2yb-1是关于x,y的单项式,系数为9,次数是3,求a、b的值.
04小结导构
01情境导入
02问题导探
03典例导练
1.单独的一个数或一个字母也是单项式;
2.当一个单项式的系数是1或-1时,通常省略不写,如x2,-a2b等
3.圆周率π是常数,把它当作系数;
4.如果单项式系数为0,它就是0次单项式.
5.单项式次数只与字母指数有关
……
本节课你收获了什么?
01情境导入
02问题导探
03典例导练
04小结导构
用含有字母的式子表示下列数量关系.
(1) 如果每年植树绿化x公顷荒山,那么这五
年内植树绿化荒山 公顷.
(2) 每本笔记本为m元,买六本笔记本需支付
元.
(3) 半径为r的圆的面积是 .
(4) 全校总人数是x,其中女生人数占了48%,
则女生人数是 .
5x
6m
0.48x
02问题导探
01情境导入
03典例导练
04小结导构
探究:观察下列所填代数式,它们有什么共同的特点吗?
5x
6m
0.48x
数字
字母
数字
字母
数字
字母
数字
字母
×
×
×
×
都是数与字母的乘积形式.
2.1.2 单项式
02问题导探
01情境导入
03典例导练
04小结导构
单项式的定义
只含有数与字母的积的式子叫做单项式.
注意:
单独的一个数或一个字母也是单项式.
比如: -3,0,m … …
02问题导探
01情境导入
03典例导练
04小结导构
判断下列各代数式是否是单项式?
⑤ ⑥
⑨ ⑩
圆周率 是常数
02问题导探
01情境导入
03典例导练
04小结导构
解剖单项式
单项式中的数字因数称为单项式的系数.
注意:单项式的系数要包括其前面的性质符号(正号可以省略,负号绝对不能落).
02问题导探
01情境导入
03典例导练
04小结导构
快速说出下列单项式的系数
单项式 22x 6a2 a3 -n vt 2πR
系数
4
在研究单项式的系数问题时,要注意以下几点:
1.当单项式的系数是1或-1时,“1”通常省略不写。
2.圆周率π是常数。
3.当单项式的系数是带分数时,通常写成假分数。
4.单项式的系数应包括它前面的性质符号。
6
1
-1
1
2
02问题导探
01情境导入
03典例导练
04小结导构
解剖单项式
所有字母指数的和称为单项式的次数
02问题导探
01情境导入
03典例导练
04小结导构
快速说出下列单项式的次数
单项式 22x 6a2 a3 -n vt 2πR
次数
1
在研究单项式的次数问题时,要注意以下几点:
1.在一个单项式中,所有字母的指数的和才叫做单项式的次数
2.单独一个数的次数记为0。
2
3
1
2
1
03典例导练
01情境导入
02问题导探
04小结导构
例1.用单项式填空,并指出它们的系数和次数.
1. 每包书有12册,n包书有_____册;
2. 底边长为a,高为h的三角形的面积是_____;
3. 一个长方体的长和宽都是a,高为h,它的体积是_____;
4. 一台电视机原价为a元,现按原价的九折出售,这台电视机 现在的售价为____;
5. 一个长方形的长为0.9,宽为a,面积是____.
12n
0.9a
0.9a
同一个式子可以表示不同的含义
12,一次
二次
1,三次
0.9,一次
0.9,一次
02问题导探
01情境导入
03典例导练
04小结导构
练习1.分别写出下列数的系数和次数:
你觉得找单项式的系数应注意什么?次数呢?
① ② ③
④ 1 ⑤ -1 ⑥ 0
03典例导练
01情境导入
02问题导探
04小结导构
练习2.判断,错误的地方请予以改正.
①-7xy2的系数是7;( )
②-x2y3与x3没有系数;( )
③-34ab3c2的次数是10;( )
④-a3的系数是-1; ( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是2( )
×
×
×
×
×
√
03典例导练
01情境导入
02问题导探
04小结导构
练习3.写出一个含有x、y,而且系数是-3,
次数是4的单项式.
x、y的指数之和为4即可
03典例导练
01情境导入
02问题导探
04小结导构
例2.
若是关于 x,y 的一个四次单项式,m,n应满足的条件?
即m≠ 2,n=2.
2+n=4,
m-2 ≠ 0
解:由题意得:
03典例导练
01情境导入
02问题导探
04小结导构
练习4.
若(-2)axby 与 的次数相同,系数的
整数部分相同,求正整数a、b的值.
03典例导练
01情境导入
02问题导探
04小结导构
当堂训练
1.下列各式是不是单项式?为什么?
2.判断下列各说法是否正确,将错误的改正过来.
(1)单项式 的系数是0, 次数是2. ( )
(2)单项式 的系数是2, 次数是10 . ( )
(3)单项式 的系数是 ,次数是n+1 . ( )
03典例导练
01情境导入
02问题导探
04小结导构
当堂训练
3.若a2x2yb-1是关于x,y的单项式,系数为9,次数是3,求a、b的值.
04小结导构
01情境导入
02问题导探
03典例导练
1.单独的一个数或一个字母也是单项式;
2.当一个单项式的系数是1或-1时,通常省略不写,如x2,-a2b等
3.圆周率π是常数,把它当作系数;
4.如果单项式系数为0,它就是0次单项式.
5.单项式次数只与字母指数有关
……
本节课你收获了什么?
