广东省肇庆市重点中学2023-2024学年高一上学期12月联考数学试题(含解析)
文档属性
| 名称 | 广东省肇庆市重点中学2023-2024学年高一上学期12月联考数学试题(含解析) | 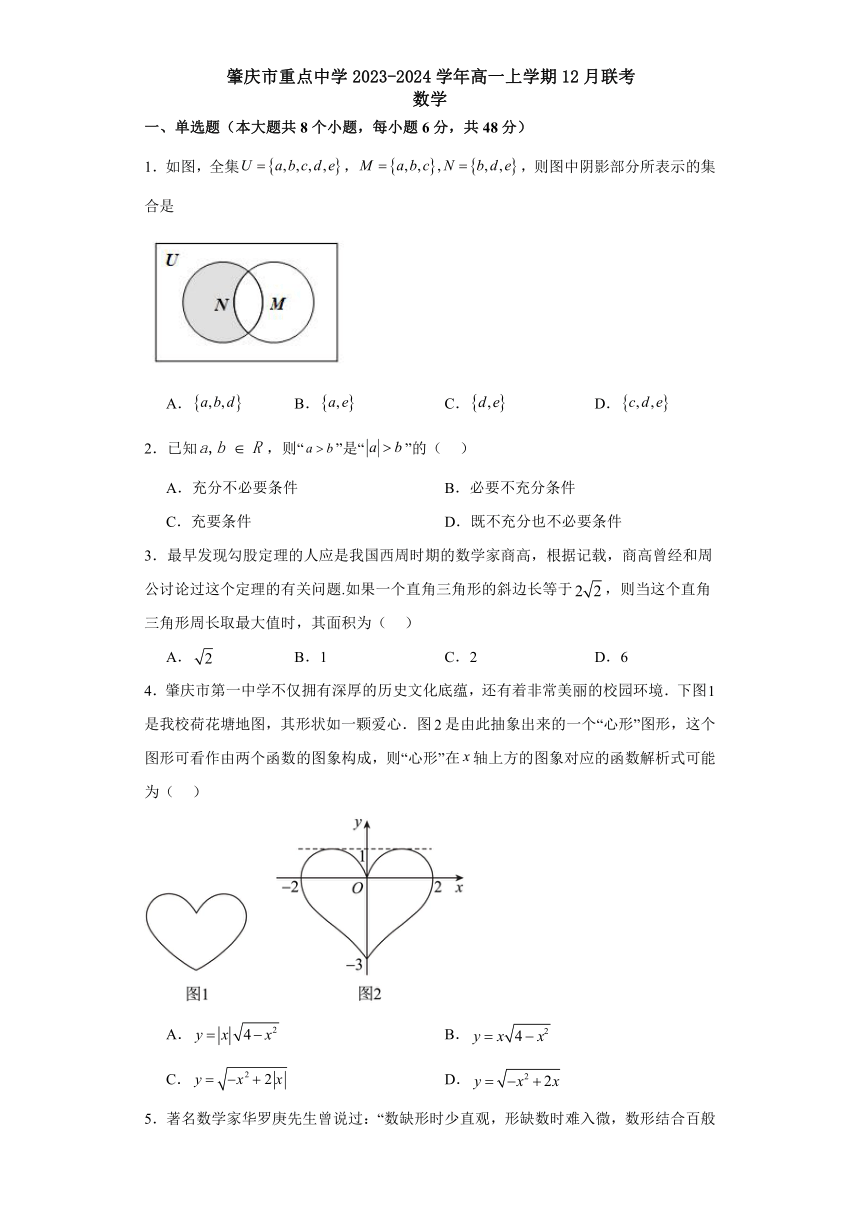 | |
| 格式 | docx | ||
| 文件大小 | 687.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 23:35:12 | ||
图片预览




文档简介
肇庆市重点中学2023-2024学年高一上学期12月联考
数学
一、单选题(本大题共8个小题,每小题6分,共48分)
1.如图,全集,,则图中阴影部分所表示的集合是
A. B. C. D.
2.已知,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.最早发现勾股定理的人应是我国西周时期的数学家商高,根据记载,商高曾经和周公讨论过这个定理的有关问题.如果一个直角三角形的斜边长等于,则当这个直角三角形周长取最大值时,其面积为( )
A. B.1 C.2 D.6
4.肇庆市第一中学不仅拥有深厚的历史文化底蕴,还有着非常美丽的校园环境.下图是我校荷花塘地图,其形状如一颗爱心.图是由此抽象出来的一个“心形”图形,这个图形可看作由两个函数的图象构成,则“心形”在轴上方的图象对应的函数解析式可能为( )
A. B.
C. D.
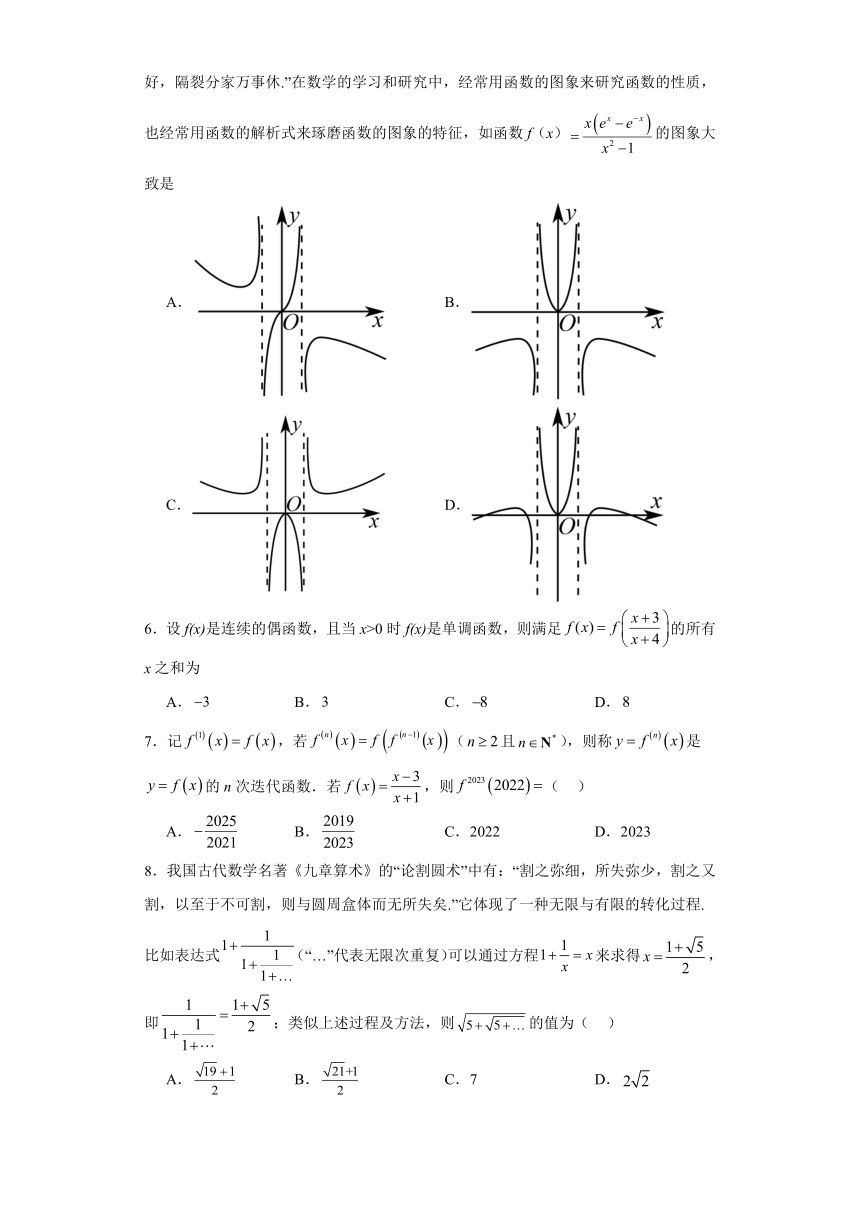
5.著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如函数f(x)的图象大致是
A. B.
C. D.
6.设f(x)是连续的偶函数,且当x>0时f(x)是单调函数,则满足的所有x之和为
A. B. C. D.
7.记,若(且),则称是的n次迭代函数.若,则( )
A. B. C.2022 D.2023
8.我国古代数学名著《九章算术》的“论割圆术”中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周盒体而无所失矣.”它体现了一种无限与有限的转化过程.比如表达式(“…”代表无限次重复)可以通过方程来求得,即;类似上述过程及方法,则的值为( )
A. B. C.7 D.
二、填空题(本大题共8个小题,每小题6分,共48分)
9.若,则 .
10.对于,不等式恒成立,则实数的取值范围是 .
11.若两个正实数满足,且不等式有解,则实数的取值范围是 .
12.若均为正数,且,则的最小值为 .
13.若命题:“任意实数使得不等式成立”为假命题,则实数的范围是 .
14.已知关于的不等式的解集是,则的取值范围是 .
15.高斯函数属于初等函数,以大数学家约翰·卡尔·弗里德里希·高斯的名字命名,高斯函数应用范围很广,在自然科学 社会科学 数学以及工程学等领域都能看到它的身影,设,用表示不超过的最大整数,则称为高斯函数,例如:,.则函数的值域为 .
16.在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,布劳威尔不动点定理得名于荷兰数学家鲁伊兹·布劳威尔(LEJBrouwer),简单的讲就是对于满足一定条件的图象不间断的函数,存在,使,那么我们称该函数为“不动点”函数,为函数的不动点.若,则的不动点为 .
三、解答题(共3小题,17题16分,18题16分,19题22分,共54分)
17.已知函数 对一切实数 都有 成立,且
(1)求 的解析式;
(2),若存在 ,使得 ,有 成立,求 的取值范围.
18.已知,满足
①求的最小值;
②当取最小值时,求的最大值.
19.已知函数,其中为常数.
(1)当时,解不等式的解集;
(2)当时,写出函数的单调区间;
(3)若在上存在个不同的实数,,使得,求实数的取值范围.
答案
1.C
解:由题意得,所以图中阴影部分所表示的集合为
2.A
解:当:
若异号,即,显然成立;
若或,均有成立;
所以充分性成立;
当:若,,显然不成立,故必要性不成立.
所以“”是“”的充分不必要条件.
3.C
解:设该直角三角形的斜边为,直角边为,,则,
因为,所以,即,
当且仅当,且,即时,等号成立.
因为,,所以,所以的最大值为4,
该直角三角形周长,
故这个直角三角形周长取最大值时,,
此时三角形的面积为.
4.C
解:对于A,(当且仅当,即时取等号),
在上的最大值为,与图象不符,A错误;
对于B,当时,,与图象不符,B错误;
对于C,,当时,;
又过点;
由得:,解得:,即函数定义域为;
又,
为定义在上的偶函数,图象关于轴对称;
当时,,则函数在上单调递增,在上单调递减;
综上所述:与图象相符,C正确;
对于D,由得:,不存在部分的图象,D错误.
5.C
解:函数的定义域为{x|x±1},
f(﹣x)f(x),则函数f(x)是偶函数,图象关于y轴对称,排除A,
当x1时,f(x)0恒成立,排除B,D,
6.C
解:试题分析:根据已知函数是连续的偶函数,且当时是单调函数,且有,则说明而来,那么解方程可知满足方程的解求解得到方程的根满足,那么结合韦达定理可知四个根的和为-8,
7.B
解:根据题意,,即,则,,,故有,
所以,故.
8.B
解:由题意,令,则,
整理得,解得,,,
9.
解:由题意,∵集合中有元素,
∴,
又∵,
∴,则,
∴,
∴,解得:或,
当时,,不满足集合中元素的互异性,故舍去;
当时,,,
满足,
∴,则.
10.
解:对于,不等式恒成立,
即的最小值大于或等于,
由绝对值的意义:表示数轴上的x对应点到和对应点的距离之和,
它的最小值为4,故,即,解得,
故实数的取值范围是.
11.
解:若不等式 有解, 即即可,
由题意可知:
,
当且仅当 , 即时, 等号成立,
可得, 即, 解得或,
所以实数 的取值范围是.
12.
解:因为均为正数,所以,则,
又因为,所以,
令,则,即,
解得或(舍去),
当且仅当时,等号成立,
所以的最小值为.
13.
解:由题意,存在实数使得不等式成立,
所以不等式的解集非空,
①当时,,得,符合题意,
②当时,不等式对应的二次函数开口向下,
故的解集显然非空,符合题意,
③当时,因为不等式的解集非空,
所以,即,解得或,
所以或,
综上或,
14.
解:关于的不等式的解集是,
所以,,且是一元二次方程的
两个根,可知,,解得:或,
所以,.又有,,.
所以,;
所以,.
15.
解:令,
所以,
因为,所以,所以,
所以,
所以,
所以函数的值域为.
16.0或1
解:设的不动点为,则由题意,又,故,即,所以,故为的不动点,故,即,解得或,即的不动点为0或1.
17.(1)
(2)
解:(1)∵函数 对一切实数 都有 成立,且 ,
令y=1,则,
.
.
(2)由题意,有,
则,
对于g(x),当x=0时,g(0)=0,
当时,,设,
则在(0,1)单调递减,在单调递增,在x=1处取到最小值,
所以,所以,
综上,,当且仅当x=1时取到,
所以;
设,则h(x)为开口向上的二次函数,其对称轴为x=a,下面通过对称轴的位置对h(x)的最值情况进行分类讨论:
当时,对称轴距离区间右侧x=2更远,故,
∴,即;
2)当时,对称轴距离区间左侧x=-1更远,故,
∴,即;
综上,.
18.①2;②
解:①因为,等号成立的条件是,所以,当时,S可取最小值2.
②当S取最小值时,,从而,;
令则从而,(负值舍去).
由在单减,因此,当时,c有最大值
19.(1)
(2)的严格增区间为和,严格减区间为
(3)
(1)解:当时,,
当时,,解得,所以,
当时,成立,
当时,,解得,
综上,不等式的解集为;
(2)解:当时,,
所以由二次函数的单调性知,的严格增区间为和,严格减区间为.
(3)解:①当时,在上单调递增,
所以
,
所以,解得;
②当时,,在上单调递增,
所以
所以,解得;
③当时,则,在上单调递增,在上单调递减,
所以
,不满足条件,
④当时,,
在、上单调递增,在上单调递减,
所以
,不满足条件,
综上,实数的取值范围为.
数学
一、单选题(本大题共8个小题,每小题6分,共48分)
1.如图,全集,,则图中阴影部分所表示的集合是
A. B. C. D.
2.已知,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.最早发现勾股定理的人应是我国西周时期的数学家商高,根据记载,商高曾经和周公讨论过这个定理的有关问题.如果一个直角三角形的斜边长等于,则当这个直角三角形周长取最大值时,其面积为( )
A. B.1 C.2 D.6
4.肇庆市第一中学不仅拥有深厚的历史文化底蕴,还有着非常美丽的校园环境.下图是我校荷花塘地图,其形状如一颗爱心.图是由此抽象出来的一个“心形”图形,这个图形可看作由两个函数的图象构成,则“心形”在轴上方的图象对应的函数解析式可能为( )
A. B.
C. D.
5.著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如函数f(x)的图象大致是
A. B.
C. D.
6.设f(x)是连续的偶函数,且当x>0时f(x)是单调函数,则满足的所有x之和为
A. B. C. D.
7.记,若(且),则称是的n次迭代函数.若,则( )
A. B. C.2022 D.2023
8.我国古代数学名著《九章算术》的“论割圆术”中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周盒体而无所失矣.”它体现了一种无限与有限的转化过程.比如表达式(“…”代表无限次重复)可以通过方程来求得,即;类似上述过程及方法,则的值为( )
A. B. C.7 D.
二、填空题(本大题共8个小题,每小题6分,共48分)
9.若,则 .
10.对于,不等式恒成立,则实数的取值范围是 .
11.若两个正实数满足,且不等式有解,则实数的取值范围是 .
12.若均为正数,且,则的最小值为 .
13.若命题:“任意实数使得不等式成立”为假命题,则实数的范围是 .
14.已知关于的不等式的解集是,则的取值范围是 .
15.高斯函数属于初等函数,以大数学家约翰·卡尔·弗里德里希·高斯的名字命名,高斯函数应用范围很广,在自然科学 社会科学 数学以及工程学等领域都能看到它的身影,设,用表示不超过的最大整数,则称为高斯函数,例如:,.则函数的值域为 .
16.在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,布劳威尔不动点定理得名于荷兰数学家鲁伊兹·布劳威尔(LEJBrouwer),简单的讲就是对于满足一定条件的图象不间断的函数,存在,使,那么我们称该函数为“不动点”函数,为函数的不动点.若,则的不动点为 .
三、解答题(共3小题,17题16分,18题16分,19题22分,共54分)
17.已知函数 对一切实数 都有 成立,且
(1)求 的解析式;
(2),若存在 ,使得 ,有 成立,求 的取值范围.
18.已知,满足
①求的最小值;
②当取最小值时,求的最大值.
19.已知函数,其中为常数.
(1)当时,解不等式的解集;
(2)当时,写出函数的单调区间;
(3)若在上存在个不同的实数,,使得,求实数的取值范围.
答案
1.C
解:由题意得,所以图中阴影部分所表示的集合为
2.A
解:当:
若异号,即,显然成立;
若或,均有成立;
所以充分性成立;
当:若,,显然不成立,故必要性不成立.
所以“”是“”的充分不必要条件.
3.C
解:设该直角三角形的斜边为,直角边为,,则,
因为,所以,即,
当且仅当,且,即时,等号成立.
因为,,所以,所以的最大值为4,
该直角三角形周长,
故这个直角三角形周长取最大值时,,
此时三角形的面积为.
4.C
解:对于A,(当且仅当,即时取等号),
在上的最大值为,与图象不符,A错误;
对于B,当时,,与图象不符,B错误;
对于C,,当时,;
又过点;
由得:,解得:,即函数定义域为;
又,
为定义在上的偶函数,图象关于轴对称;
当时,,则函数在上单调递增,在上单调递减;
综上所述:与图象相符,C正确;
对于D,由得:,不存在部分的图象,D错误.
5.C
解:函数的定义域为{x|x±1},
f(﹣x)f(x),则函数f(x)是偶函数,图象关于y轴对称,排除A,
当x1时,f(x)0恒成立,排除B,D,
6.C
解:试题分析:根据已知函数是连续的偶函数,且当时是单调函数,且有,则说明而来,那么解方程可知满足方程的解求解得到方程的根满足,那么结合韦达定理可知四个根的和为-8,
7.B
解:根据题意,,即,则,,,故有,
所以,故.
8.B
解:由题意,令,则,
整理得,解得,,,
9.
解:由题意,∵集合中有元素,
∴,
又∵,
∴,则,
∴,
∴,解得:或,
当时,,不满足集合中元素的互异性,故舍去;
当时,,,
满足,
∴,则.
10.
解:对于,不等式恒成立,
即的最小值大于或等于,
由绝对值的意义:表示数轴上的x对应点到和对应点的距离之和,
它的最小值为4,故,即,解得,
故实数的取值范围是.
11.
解:若不等式 有解, 即即可,
由题意可知:
,
当且仅当 , 即时, 等号成立,
可得, 即, 解得或,
所以实数 的取值范围是.
12.
解:因为均为正数,所以,则,
又因为,所以,
令,则,即,
解得或(舍去),
当且仅当时,等号成立,
所以的最小值为.
13.
解:由题意,存在实数使得不等式成立,
所以不等式的解集非空,
①当时,,得,符合题意,
②当时,不等式对应的二次函数开口向下,
故的解集显然非空,符合题意,
③当时,因为不等式的解集非空,
所以,即,解得或,
所以或,
综上或,
14.
解:关于的不等式的解集是,
所以,,且是一元二次方程的
两个根,可知,,解得:或,
所以,.又有,,.
所以,;
所以,.
15.
解:令,
所以,
因为,所以,所以,
所以,
所以,
所以函数的值域为.
16.0或1
解:设的不动点为,则由题意,又,故,即,所以,故为的不动点,故,即,解得或,即的不动点为0或1.
17.(1)
(2)
解:(1)∵函数 对一切实数 都有 成立,且 ,
令y=1,则,
.
.
(2)由题意,有,
则,
对于g(x),当x=0时,g(0)=0,
当时,,设,
则在(0,1)单调递减,在单调递增,在x=1处取到最小值,
所以,所以,
综上,,当且仅当x=1时取到,
所以;
设,则h(x)为开口向上的二次函数,其对称轴为x=a,下面通过对称轴的位置对h(x)的最值情况进行分类讨论:
当时,对称轴距离区间右侧x=2更远,故,
∴,即;
2)当时,对称轴距离区间左侧x=-1更远,故,
∴,即;
综上,.
18.①2;②
解:①因为,等号成立的条件是,所以,当时,S可取最小值2.
②当S取最小值时,,从而,;
令则从而,(负值舍去).
由在单减,因此,当时,c有最大值
19.(1)
(2)的严格增区间为和,严格减区间为
(3)
(1)解:当时,,
当时,,解得,所以,
当时,成立,
当时,,解得,
综上,不等式的解集为;
(2)解:当时,,
所以由二次函数的单调性知,的严格增区间为和,严格减区间为.
(3)解:①当时,在上单调递增,
所以
,
所以,解得;
②当时,,在上单调递增,
所以
所以,解得;
③当时,则,在上单调递增,在上单调递减,
所以
,不满足条件,
④当时,,
在、上单调递增,在上单调递减,
所以
,不满足条件,
综上,实数的取值范围为.
同课章节目录
