等腰三角形复习课
图片预览



文档简介
课件18张PPT。等腰三角形复习课1.等腰三角形腰=腰 底边底角=底角 顶角注意! 两种情况+检验例1.等腰三角形的周长为17cm,其中一边长
为4cm,则该等腰三角形的底边长为______.
例2.等腰三角形的一个角是70°,则它的顶角
度数为______;若一个角为100°,则它的顶角
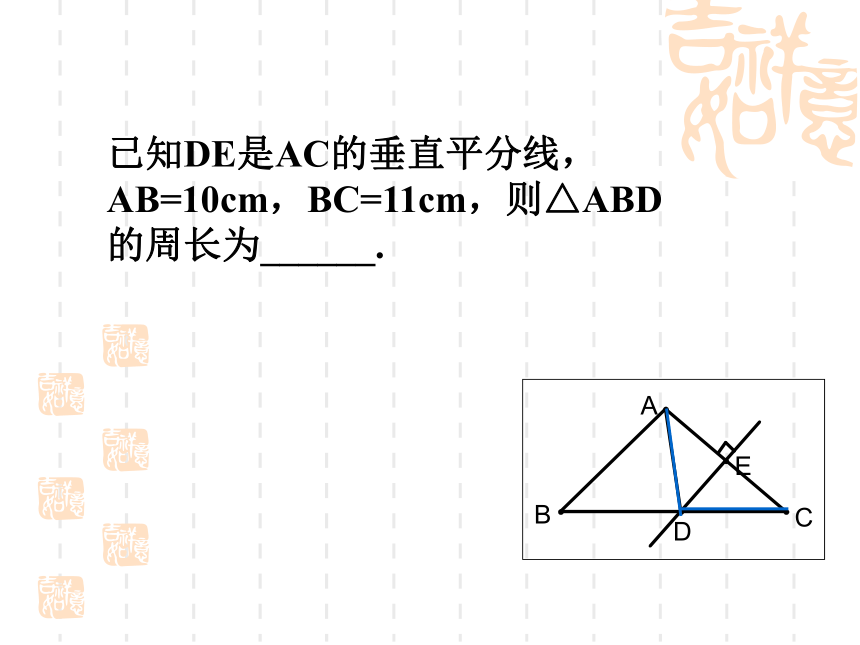
度数为______.比一比!谁更快! 2. 若等腰三角形的一个内角是45°,则它的顶角为90°( ) 1.若等腰三角形两条边的长分别是5和8,则它的周长为 .21或18NO(Yes or no!)已知DE是AC的垂直平分线,
AB=10cm,BC=11cm,则△ABD
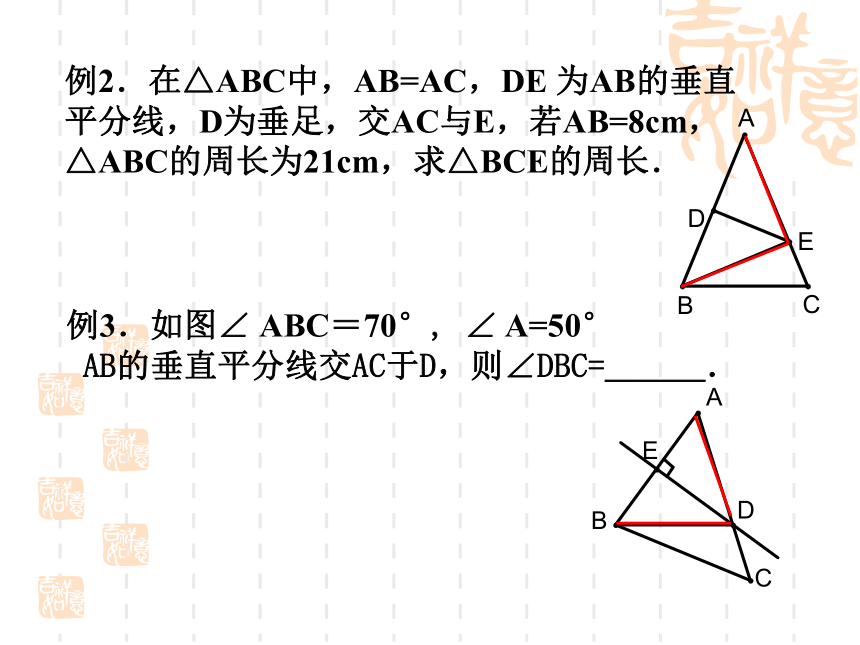
的周长为______.例2.在△ABC中,AB=AC,DE 为AB的垂直
平分线,D为垂足,交AC与E,若AB=8cm,
△ABC的周长为21cm,求△BCE的周长.例3.如图∠ ABC=70°, ∠ A=50°
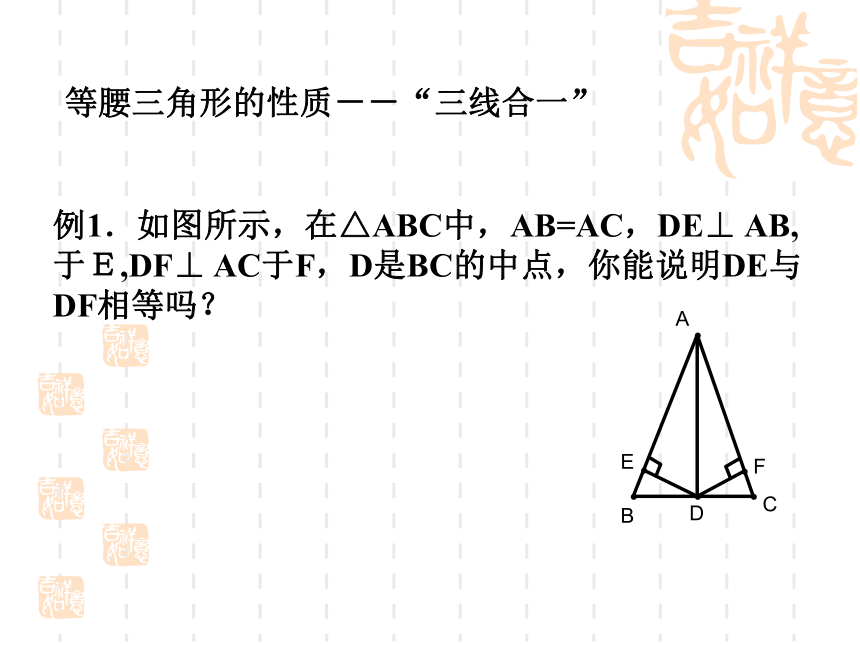
AB的垂直平分线交AC于D,则∠DBC=___. 等腰三角形的性质--“三线合一”例1.如图所示,在△ABC中,AB=AC,DE⊥ AB,
于E,DF⊥ AC于F,D是BC的中点,你能说明DE与
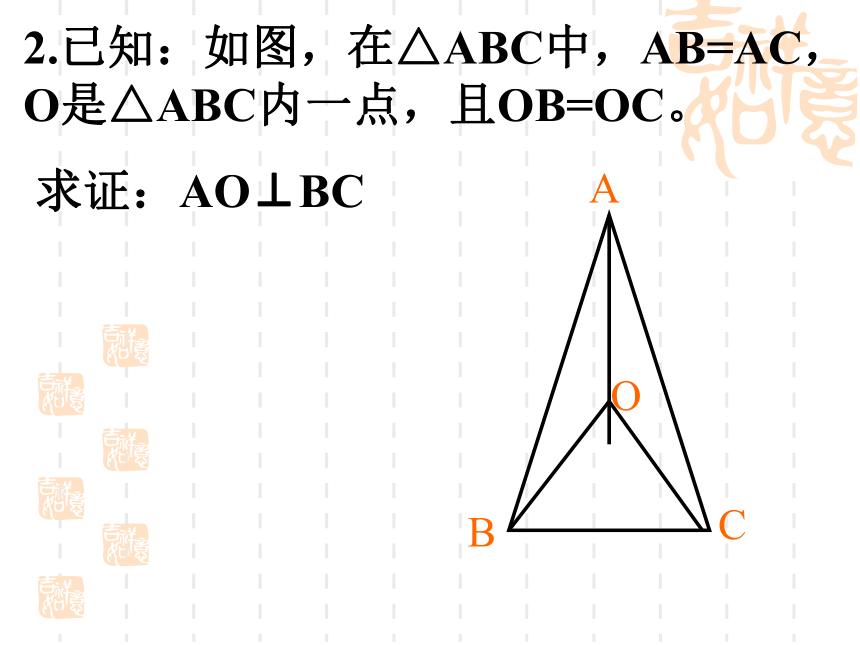
DF相等吗?2.已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC。
求证:AO⊥BCC如图:在三角形ABC中,AB=AC , D在 AC上,且BD=BC=AD,求△ABC各内角的度数?问题解析讨论:2、∠A与哪些角相等?1、∠C与哪些角相等?(∠3、 ∠ABC )123( ∠1、 ∠2 )3、 ∠C与∠A是什么关系?( ∠C=2 ∠A )解:∵BD=AD, ∴ ∠1= ∠A∵ ∠3= ∠1+ ∠A, ∴ ∠3=2 ∠A∵ BD=BC, ∴ ∠3= ∠C, ∴ ∠C=2 ∠A∵ AB=AC, ∴ ∠ABC= ∠C=2 ∠A∵ ∠A+ ∠ABC+ ∠C=1800, ∴ 5 ∠A=1800,
∴ ∠A=360, ∴ ∠ABC= ∠C=2 ∠A=720CABO 等腰直角三角形ABC两底角的平分线AO与BO交于点O, 过O点作底边AB的平行线交AC于点F,交BC于点E. 则:
3. 若AC=10,则△CEF的周长为多少?2. AF、FE、EB三条线段的长度有何关系?1. 图中有几个等腰三角形?
AF+ EB=FE相等角之间的转化相等线段之间的转化让我们继续探索:如图(二)当AC=12,BC=8.求△CFE的周长?
解:因为OA平分∠CAB.
所以∠FAO=∠OAB.
又因为EF∥AB.
所以∠FOA=∠OAB.
所以∠FAO=∠FOA
即:AF=OF 所以AC=AF+FC=OF+FC.
同理可得:BC=BE+EC=OE+EC.
所以△CFE的周长: =OF+FC+OE+EC
=AC+BC=12+8=20如图, △ABC中,∠ABC=500, ∠ACB=800,
延长 CB至D,使DB=BA,
延长BC至E,使CE=CA,连接AD,AE,
求∠D,∠E,∠DAE如图,P、Q是△ABC边上的两点,BP=PQ=QC=AP=AQ,
求∠BAC的度数。在三角形ABC中,CD是斜边AB边上的高, ∠A=30°
求证:BD= AB如图,AD是△ABC的角平分线,DE,DF分别是△ABD和
△ACD的高,
求证:AD垂直平分EF.尺规作图尺规作角的平分线尺规作线段的垂直平分线作点关于直线的对应点例1.如图所示,P、Q为△ABC 边AB与AC上两点,
在BC上求作一点M,使△PQM的周长最小.如图,求作一点P,使PC=PD,并且使点P
到∠AOB 的两边的距离相等,并说明理由.如图,求作一点P,使PC=PD,并且使点P
到∠AOB 的两边的距离相等,并说明理由.
为4cm,则该等腰三角形的底边长为______.
例2.等腰三角形的一个角是70°,则它的顶角
度数为______;若一个角为100°,则它的顶角
度数为______.比一比!谁更快! 2. 若等腰三角形的一个内角是45°,则它的顶角为90°( ) 1.若等腰三角形两条边的长分别是5和8,则它的周长为 .21或18NO(Yes or no!)已知DE是AC的垂直平分线,
AB=10cm,BC=11cm,则△ABD
的周长为______.例2.在△ABC中,AB=AC,DE 为AB的垂直
平分线,D为垂足,交AC与E,若AB=8cm,
△ABC的周长为21cm,求△BCE的周长.例3.如图∠ ABC=70°, ∠ A=50°
AB的垂直平分线交AC于D,则∠DBC=___. 等腰三角形的性质--“三线合一”例1.如图所示,在△ABC中,AB=AC,DE⊥ AB,
于E,DF⊥ AC于F,D是BC的中点,你能说明DE与
DF相等吗?2.已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC。
求证:AO⊥BCC如图:在三角形ABC中,AB=AC , D在 AC上,且BD=BC=AD,求△ABC各内角的度数?问题解析讨论:2、∠A与哪些角相等?1、∠C与哪些角相等?(∠3、 ∠ABC )123( ∠1、 ∠2 )3、 ∠C与∠A是什么关系?( ∠C=2 ∠A )解:∵BD=AD, ∴ ∠1= ∠A∵ ∠3= ∠1+ ∠A, ∴ ∠3=2 ∠A∵ BD=BC, ∴ ∠3= ∠C, ∴ ∠C=2 ∠A∵ AB=AC, ∴ ∠ABC= ∠C=2 ∠A∵ ∠A+ ∠ABC+ ∠C=1800, ∴ 5 ∠A=1800,
∴ ∠A=360, ∴ ∠ABC= ∠C=2 ∠A=720CABO 等腰直角三角形ABC两底角的平分线AO与BO交于点O, 过O点作底边AB的平行线交AC于点F,交BC于点E. 则:
3. 若AC=10,则△CEF的周长为多少?2. AF、FE、EB三条线段的长度有何关系?1. 图中有几个等腰三角形?
AF+ EB=FE相等角之间的转化相等线段之间的转化让我们继续探索:如图(二)当AC=12,BC=8.求△CFE的周长?
解:因为OA平分∠CAB.
所以∠FAO=∠OAB.
又因为EF∥AB.
所以∠FOA=∠OAB.
所以∠FAO=∠FOA
即:AF=OF 所以AC=AF+FC=OF+FC.
同理可得:BC=BE+EC=OE+EC.
所以△CFE的周长: =OF+FC+OE+EC
=AC+BC=12+8=20如图, △ABC中,∠ABC=500, ∠ACB=800,
延长 CB至D,使DB=BA,
延长BC至E,使CE=CA,连接AD,AE,
求∠D,∠E,∠DAE如图,P、Q是△ABC边上的两点,BP=PQ=QC=AP=AQ,
求∠BAC的度数。在三角形ABC中,CD是斜边AB边上的高, ∠A=30°
求证:BD= AB如图,AD是△ABC的角平分线,DE,DF分别是△ABD和
△ACD的高,
求证:AD垂直平分EF.尺规作图尺规作角的平分线尺规作线段的垂直平分线作点关于直线的对应点例1.如图所示,P、Q为△ABC 边AB与AC上两点,
在BC上求作一点M,使△PQM的周长最小.如图,求作一点P,使PC=PD,并且使点P
到∠AOB 的两边的距离相等,并说明理由.如图,求作一点P,使PC=PD,并且使点P
到∠AOB 的两边的距离相等,并说明理由.
