【深圳专用】九上数学反比例函数压轴专项训练02
文档属性
| 名称 | 【深圳专用】九上数学反比例函数压轴专项训练02 |  | |
| 格式 | docx | ||
| 文件大小 | 973.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 16:15:33 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2023年12月5日初三数学作业
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.(2023上·广东深圳·九年级深圳市高级中学校考期中)建筑是一门不断演化和创新的艺术,从古代的大理石殿堂到现代的钢铁森林,它的魅力在于其无限的可能性.近年来,一种名为双曲铝单板的新兴材料以其独特的曲线和光泽,为建筑注入了新的时尚元素,同时也赋予了建筑更多的创意和流动性.
图2为某广东厂家设计制造的双曲铝单板建筑的横截面,可以看作由两条曲线、(反比例函数图像的一支)和若干线段围成,其中四边形与四边形均为矩形,,,,,,如图2所示,取中点,以点为原点,所在直线为轴建立平面直角坐标系.
请回答下列问题:
(1)如图2,求所在双曲线的解析式;
(2)如图3,为在曲面实现自动化操作,工程师安装了支架,并加装了始终垂直于的伸缩机械臂用来雕刻所在曲面的花纹,请问点在上滑动过程中,最长为多少米?
(3)如图4,为通风透气避免潮湿,在某一时刻,打开遮光板,太阳光线经点恰好照射到点,请求出此时线段上光线无法直射部分即线段的长.
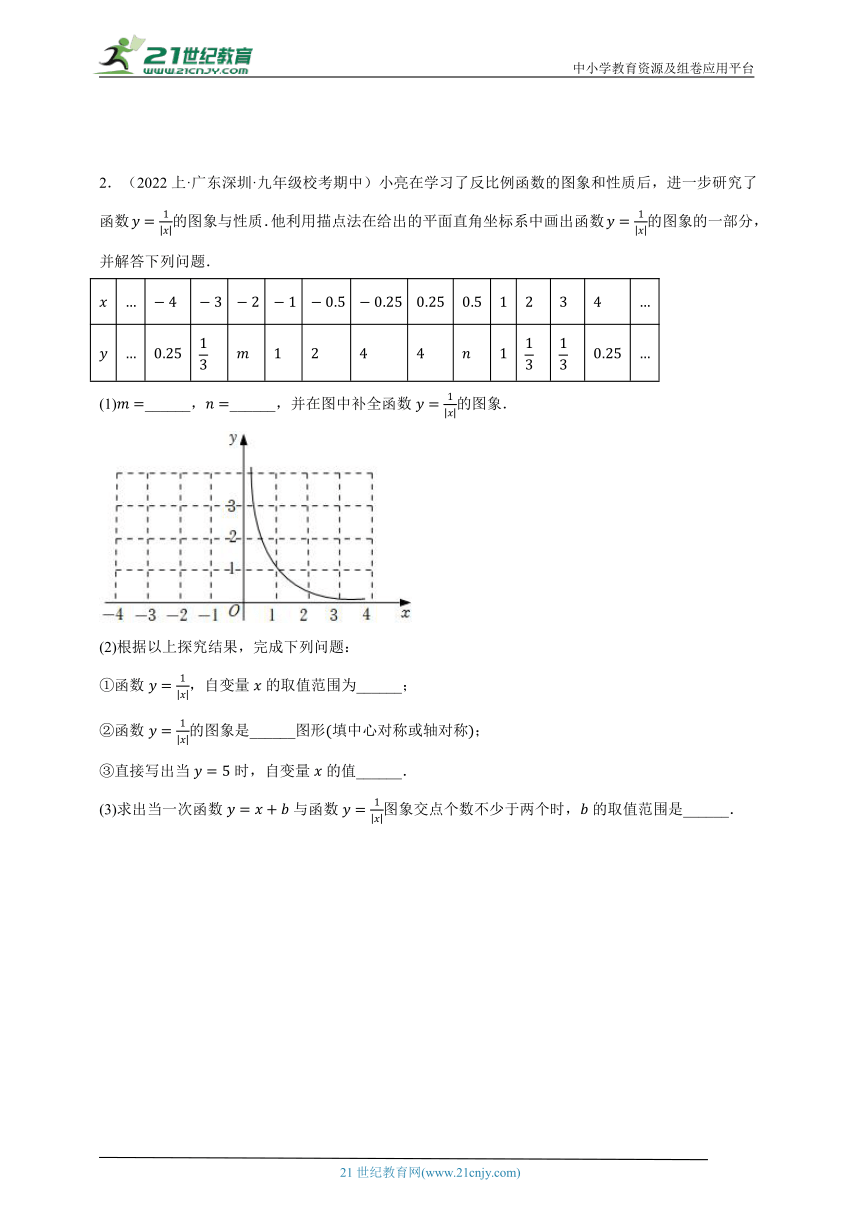
2.(2022上·广东深圳·九年级校考期中)小亮在学习了反比例函数的图象和性质后,进一步研究了函数的图象与性质.他利用描点法在给出的平面直角坐标系中画出函数的图象的一部分,并解答下列问题.
(1)______,______,并在图中补全函数的图象.
(2)根据以上探究结果,完成下列问题:
①函数,自变量的取值范围为______;
②函数的图象是______图形填中心对称或轴对称;
③直接写出当时,自变量的值______.
(3)求出当一次函数与函数图象交点个数不少于两个时,的取值范围是______.
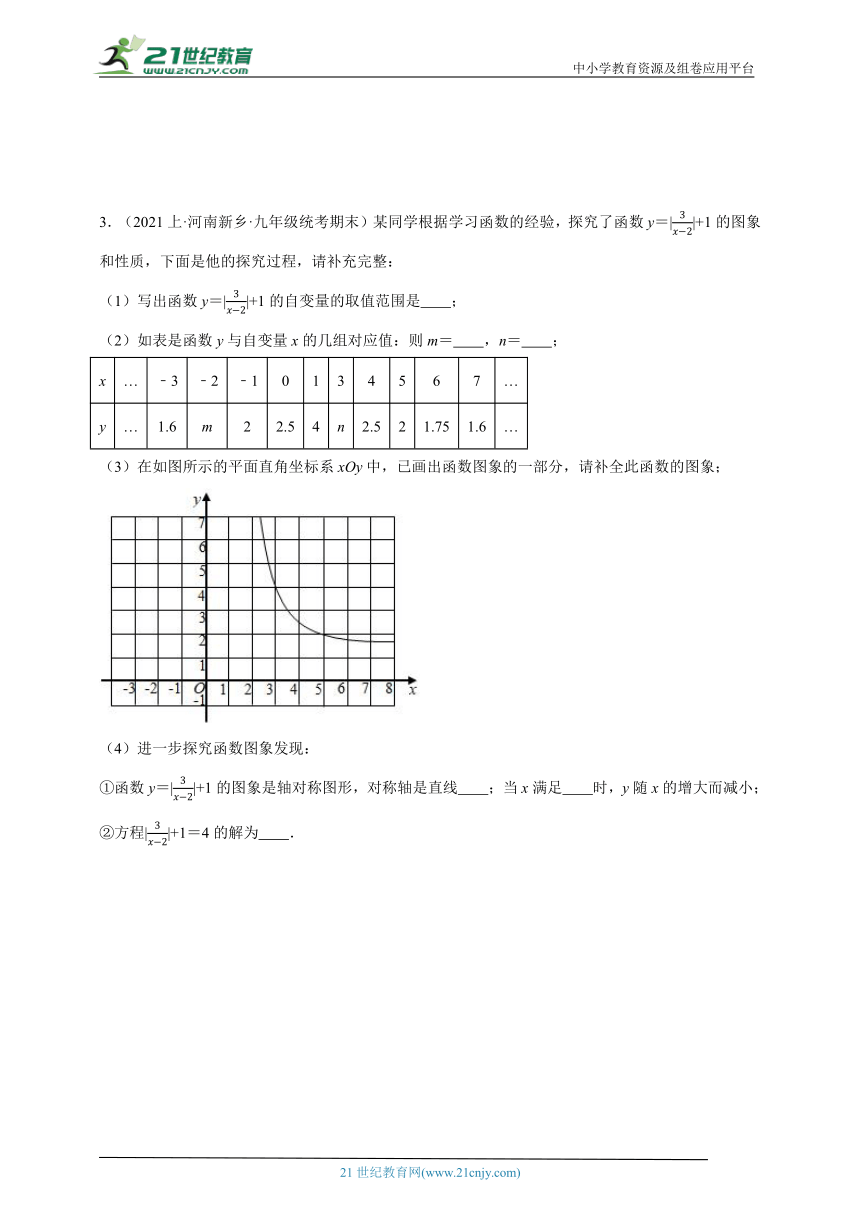
3.(2021上·河南新乡·九年级统考期末)某同学根据学习函数的经验,探究了函数y=||+1的图象和性质,下面是他的探究过程,请补充完整:
(1)写出函数y=||+1的自变量的取值范围是 ;
(2)如表是函数y与自变量x的几组对应值:则m= ,n= ;
x … ﹣3 ﹣2 ﹣1 0 1 3 4 5 6 7 …
y … 1.6 m 2 2.5 4 n 2.5 2 1.75 1.6 …
(3)在如图所示的平面直角坐标系xOy中,已画出函数图象的一部分,请补全此函数的图象;
(4)进一步探究函数图象发现:
①函数y=||+1的图象是轴对称图形,对称轴是直线 ;当x满足 时,y随x的增大而减小;
②方程||+1=4的解为 .
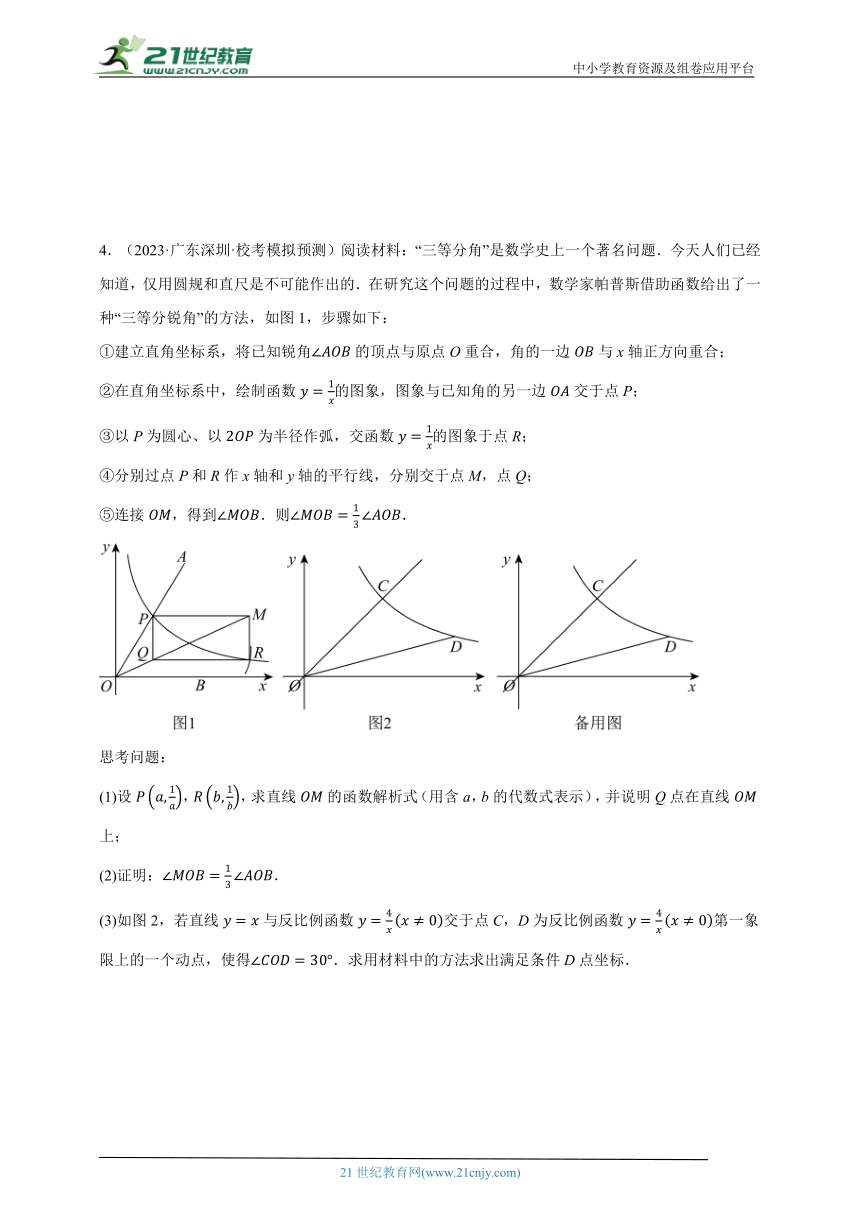
4.(2023·广东深圳·校考模拟预测)阅读材料:“三等分角”是数学史上一个著名问题.今天人们已经知道,仅用圆规和直尺是不可能作出的.在研究这个问题的过程中,数学家帕普斯借助函数给出了一种“三等分锐角”的方法,如图1,步骤如下:
①建立直角坐标系,将已知锐角的顶点与原点O重合,角的一边与x轴正方向重合;
②在直角坐标系中,绘制函数的图象,图象与已知角的另一边交于点P;
③以P为圆心、以为半径作弧,交函数的图象于点R;
④分别过点P和R作x轴和y轴的平行线,分别交于点M,点Q;
⑤连接,得到.则.
思考问题:
(1)设,,求直线的函数解析式(用含a,b的代数式表示),并说明Q点在直线上;
(2)证明:.
(3)如图2,若直线与反比例函数交于点C,D为反比例函数第一象限上的一个动点,使得.求用材料中的方法求出满足条件D点坐标.
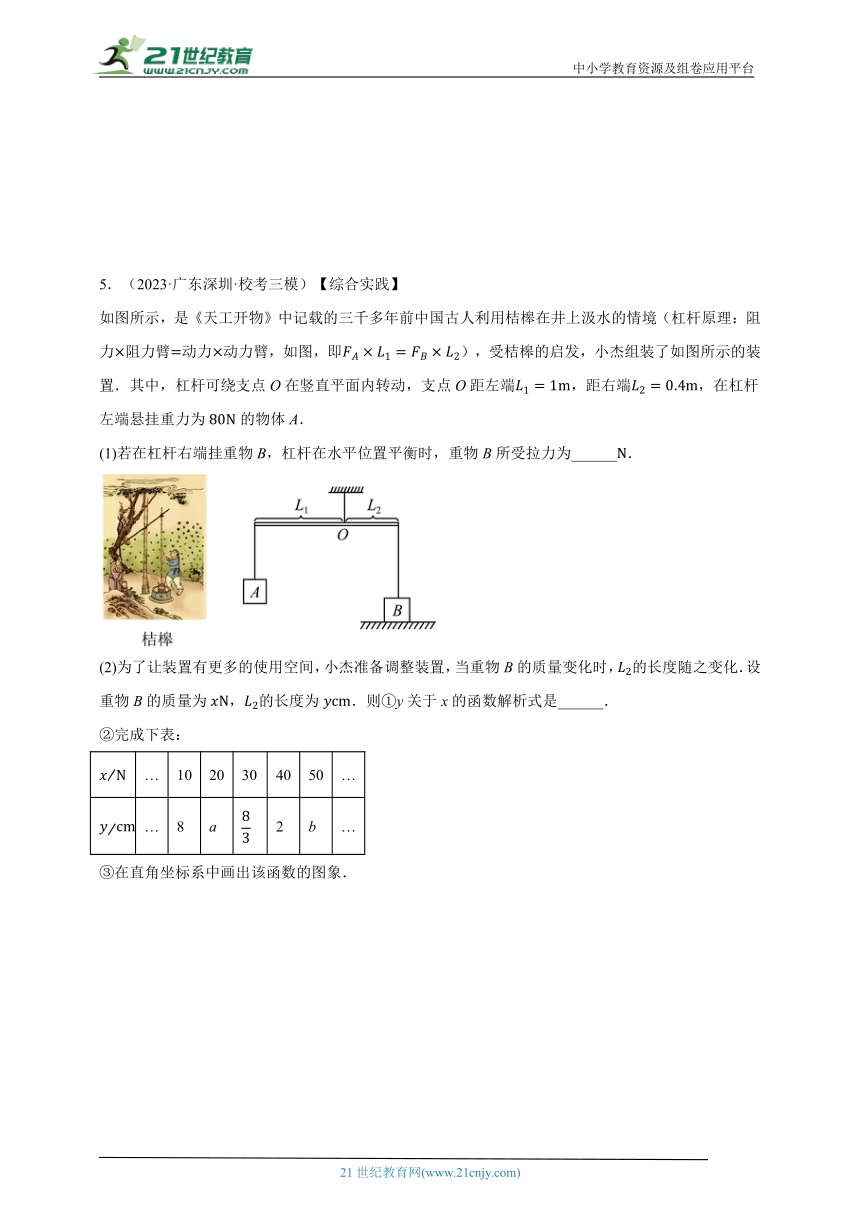
5.(2023·广东深圳·校考三模)【综合实践】
如图所示,是《天工开物》中记载的三千多年前中国古人利用桔槔在井上汲水的情境(杠杆原理:阻力阻力臂动力动力臂,如图,即),受桔槔的启发,小杰组装了如图所示的装置.其中,杠杆可绕支点O在竖直平面内转动,支点O距左端,距右端,在杠杆左端悬挂重力为的物体A.
(1)若在杠杆右端挂重物B,杠杆在水平位置平衡时,重物B所受拉力为______.
(2)为了让装置有更多的使用空间,小杰准备调整装置,当重物B的质量变化时,的长度随之变化.设重物B的质量为,的长度为.则①y关于x的函数解析式是______.
②完成下表:
… 10 20 30 40 50 …
… 8 a 2 b …
③在直角坐标系中画出该函数的图象.
(3)在(2)的条件下,将函数图象向右平移4个单位长度,与原来的图像组成一个新的函数图象,记为L.若点A的坐标为,在L上存在点Q,使得.请直接写出所有满足条件的点Q的坐标.
6.(2023·广东深圳·校考一模)【定义】在平面内,把一个图形上任意一点与另一个图形上任意一点之间的距离的最小值,称为这两个图形之间的距离,即A,B分别是图形M和图形N上任意一点,当的长最小时,称这个最小值为图形M与图形N之间的距离.
例如,如图1,,线段的长度称为点A与直线之间的距离,当时,线段的长度也是与之间的距离.
【应用】
(1)如图2,在等腰中,,,点D为边上一点,过点D作交于点E.若,,则与之间的距离是 ;
(2)如图3,已知直线与双曲线交于与B两点,点A与点B之间的距离是 ,点O与双曲线之间的距离是 ;
【拓展】
(3)按规定,住宅小区的外延到高速路的距离不超过时,需要在高速路旁修建与高速路相同走向的隔音屏障(如图4).有一条“东南 西北”走向的笔直高速路,路旁某住宅小区建筑外延呈双曲线的形状,它们之间的距离小于.现以高速路上某一合适位置为坐标原点,建立如图5所示的直角坐标系,此时高速路所在直线的函数表达式为,小区外延所在双曲线的函数表达式为,那么需要在高速路旁修建隔音屏障的长度是多少?
7.(2023下·广东深圳·九年级校联考阶段练习)在平面直角坐标系中,如果一个点的横坐标与纵坐标相等,则称该点为“不动点”
例如、、都是“不动点”,已知双曲线
(1)下列说法不正确的是( )
A.直线的图象上有无数个“不动点”
B.函数的图象上没有“不动点”
C.直线的图象上有无数个“不动点”
D.函数的图象上有两个“不动点”
(2)求双曲线上的“不动点”;
(3)若抛物线(、为常数)上有且只有一个“不动点”,
①当时,求的取值范围.
②如果,过双曲线图象上第一象限的“不动点”作平行于轴的直线,若抛物线上有四个点到的距离为,直接写出的取值范围.
8.(2022·广东深圳·深圳市宝安中学(集团)校考三模)y=x+是一种类似于反比例函数的对勾函数,形如y=ax+.其函数图像形状酷似双勾,故称“对勾函数”,也称“勾勾函数”、“海鸥函数”.y=x+函数图像如下图所示.根据y=x+图像对函数y=|x|+的图像和性质进行了探究.
(1)绘制函数图像:y=|x|+
列表:下表是x与y的几组对应值
x ……… -3 -2 -1 - - 1 2 3 ………
y ……… 2 2 ………
描点:根据表中各组对应值,在平面直角坐标系中描出各点;
连线:用平滑的曲线顺次连接各点,请你在平面直角坐标系中将y=|x|+图像补充完整;
(2)观察发现:
①写出函数y=|x|+的一条性质_________
②函数图像与直线y=2有_________个交点,
所以对应的方程|x|+有_________个实数根.
(3)分析思考:
③方程的|x-1|+-2=0的解为_________
④不等式|x|+-<0,x的取值范围为_________
(4)延伸探究:
⑤当x>0时,直线y=kx+3与y=|x|+只有一个交点,求k的值?
9.(2022·广东深圳·模拟预测)【建模】某班开端午联欢会,生活委员彤彤先购买了2个装饰挂件共计3元,又购买了单价为2元的粽形香囊x个,设y(元)是所有装饰挂件和粽形香囊的平均价格,则y与x的关系式为 .
【探究】根据函数的概念,彤彤发现:y是x的函数.结合自己学习函数的经验,为了更好地研究这个函数,彤彤打算先脱离实际背景,对该函数的完整图象与性质展开探究.请根据所给信息,将彤彤的探究过程补充完整:
(1)列表:
x … ﹣4 ﹣3 ﹣1 0 …
y … …
(2)在平面直角坐标系中描点、连线,画出该函数图象:
(3)观察图象,彤彤发现以下性质:
①该函数图象是中心对称图形,对称中心是 ;
②该函数值y不可能等于 ;
③当x>﹣2时,y随x的增大而 (填“增大”或者“减小”),当x<﹣2时,亦是如此.
【应用】根据上述探究,结合实际经验,彤彤得到结论:粽形香囊越多,所购买物品的平均价格越 (填“高”或者“低”),但不会突破 元.
10.(2022·广东深圳·统考二模)在并联电路中,电源电压为,小亮根据“并联电路分流不分压”的原理知道:(,).已知R1为定值电阻,当R变化时,干路电流也会发生变化,且干路电流与R之间满足如下关系:.
(1)定值电阻的阻值为__________;
(2)小亮根据学习函数的经验,参照研究函数的过程与方法,对比反比例函数来探究函数的图象与性质.
①列表:下表列出点与R的几组对应值,请写出m,n的值:__________,__________;
R … 3 4 5 6 …
… 2 1.5 1.2 1 …
… 3 m 2.2 n …
②描点、连线:在平面直角坐标系中,以①给出的R的取值为横坐标,以相对应的值为纵坐标,描出相应的点,并将各点用光滑曲线顺次连接起来;
(3)观察图象并分析表格,回答下列问题:
①随R的增大而__________;(填“增大”或“减小”)
②函数的图象是由的图象向__________平移__________个单位而得到.
参考答案:
1.(1);
(2)
(3)8
【分析】(1)根据题意可得,再利用待定系数法解答,即可求解;
(2)先求出所在直线解析式为,再根据反比例函数图像轴对称的性质,可得曲线关于直线轴对称,然后联立,即可求解;
(3)先求出所在直线解析式为,再根据,可设直线解析式为,然后,整理得:,利用一元二次方程根的判别式,可得,从而得到,进而得到解析式为,即可求解.
【详解】(1)解:,,,为中点,,
,
设所在双曲线的表达式为,
将点坐标代入表达式中,得:
解得:,
抛物线表达式为;
(2)解:根据题意得:点与点坐标分别为,,
设所在直线解析式为,
将、两点坐标代入得:,
解得,,
所在直线解析式为,
根据反比例函数图像轴对称的性质,曲线关于直线轴对称,
联立,解得,
联立,解得,
,
(3)解:如图,光线与曲线只有一个交点,
设直线的解析式为,
将点,点代入得:,
解得,,
所在直线解析式为,
∵,
可设直线解析式为,
∴,
整理得:
∴
解得:,(舍去),
解析式为,
将分别代入,
解得:,
∴点,点,点点,
.
【点睛】本题主要查了反比例函数的实际应用,一元二次方程根的判别式,利用数形结合思想解答是解题的关键.
2.(1),,图见解析
(2)①;②轴对称;③或
(3)
【分析】(1)利用函数解析式分别求出对应的函数值,利用描点法画出图象即可.
(2)观察图象即可得到结论.
(3)利用图象即可解决问题.
【详解】(1)把,代入得,把代入得,
,.
故答案为:,.
画出函数的图象如图所示,
;
(2)观察函数图象,
函数,自变量的取值范围为;
函数的图象是轴对称图形填中心对称或轴对称;
当时,自变量的值是或
故答案为:,轴对称,或.
(3)如图,
当直线过时,函数的图象与函数的图象有两个交点,此时,
由图象可知,当时,函数的图象与函数的图象交点个数不少于两个,
故答案为:.
【点睛】本题是反比例函数与一次函数的交点问题,考查反比例函数的图象与性质,数形结合是解题的关键.
3.(1)x≠2;(2), 4;(3)见解析;(4)①x=2,x>2;②x1=1,x2=3.
【分析】(1)分母不为零;
(2)把x=-2和3分别代入y=||+1即可求得;
(3)画出函数图象即可;
(4)根据图象得出结论.
【详解】解:(1)函数y=||+1的自变量x的取值范围是:x≠2;
(2)把x=﹣2和3分别代入y=||+1得,m=+1=,n=3+1=4,
故答案为,4;
(3)如图所示;
(4)由图象发现:①函数y=||+1的图象是轴对称图形,对称轴是直线x=2;当x满足x>2时,y随x的增大而减小;
故答案为x=2,x>2;
②方程||+1=4的解为x1=1,x2=3,
故答案为x1=1,x2=3.
【点睛】此题考查了反比例函数图象和性质,涉及的知识有:自变量的取值范围、画图象、熟练掌握数形结合的思想是解本题的关键.
4.(1),证明见解析
(2)见解析
(3)或
【分析】(1)由轴,轴,,,即可得出M点的坐标,即可,再将点Q的坐标代入解析式即可判断点Q是否在直线上;
(2)连接,交于点S,由矩形的性质和平行线的性质即可得到结论;
(3)先求出点,可得,然后分两种情况讨论:当D点在下方时,当D点在上方时,即可求解.
【详解】(1)解:设直线的函数表达式为,
由题意得:,
∴四边形为矩形,
∵,,
∴,,
把点代入得:,
∴直线的函数表达式为,
∵的坐标满足,
∴点Q在直线上;
(2)解:连接,交于点S,
由题意得四边形是矩形,
∴,,,
∴,
∴,
∴
∵,
∴.
∴,
∵轴,
∴,
∴,即.
(3)解:∵直线与反比例函数交于点C,
∴,解得:或(舍去),
∴,
∴,
当D点在下方时,如图,以C为圆心,为半径画弧,交反比例函数于点E,作轴,作轴,连接并延长交反比例与点F,作,连接,与交于点H,,,,
作于I,则,,,
,
则,,
即,
同理,当D点在上方时,有.
【点睛】此题在考查三等分角的作法时,综合考查了待定系数法求函数解析式的方法、矩形的性质以及三角形外角的性质等,综合性较强.
5.(1)
(2)①;②见解析;③见解析
(3)或
【分析】(1)根据公式进行计算即可;
(2)①根据公式即可得到;②根据(2)①所求求出a、b的值即可;③先描点,再连线,画出函数图象即可;
(3)先根据面积求出点Q的纵坐标,再根据反比例函数性质和平移的性质求出点Q的坐标即可.
【详解】(1)解:∵,
∴
∴重物B所受拉力为,
故答案为:;
(2)解:①∵,
∴,即,
故答案为:;
②由(2)①得,
填表如下:
… 10 20 30 40 50 …
… 8 4 2 …
③函数图象如下所示:
(3)解:∵点A的坐标为,
∴,
∵,
∴,
∴,
在中,当时,
∴在函数上满足题意的Q的坐标为,
∵将函数图象向右平移4个单位长度,与原来的图像组成一个新的函数图象,记为L,
∴点,即也在L上,即满足题意的Q的坐标为;
综上所述,点Q的坐标为或.
【点睛】本题主要考查了反比例函数的实际运用,正确理解题意是解题的关键.
6.(1);(2),;(3)80米
【分析】(1)过点D作于点H,得出是等腰直角三角形,根据等腰直角三角形的性质求出结果即可;
(2)先根据一次函数解析式求出,然后再求出反比例函数解析式,再求出点,根据两点点距离公式求出的值即可;作,且与双曲线只有一个交点,设直线的解析式为,求出一次函数解析式,再求出交点坐标,最后求出的值即可;
(3)作直线,设的解析式为,与双曲线交于点A、B,过点O作于点P,过点P作轴于点H,过点A、B分别作直线的垂线、,垂足为E、F,先求出直线的解析式,然后求出点A、B的坐标,根据两点之间距离公式求出的长,进而即可得出答案.
【详解】解:(1)如图,过点D作于点H,
∵,,
∴,
∵,
∴是等腰直角三角形,
∴,
∵,,
∴,
∴;
故答案为:;
(2)把代入中,得:,
∴,
把代入,得:,
∴,
∴双曲线的解析式为,
联立,得:,
即,
解得:,,
∴,
∴;
如图,作,且与双曲线只有一个交点,设直线的解析式为,
则,
整理得:,
∴,
∴或(不符合题意,舍去),
∴直线的解析式为,
由,
解得:,
∴,
∴;
故答案为:;.
(3)如图,作直线,设的解析式为,与双曲线交于点A、B,过点O作于点P,过点P作轴于点H,过点A、B分别作直线的垂线、,垂足为E、F,
则,
∵直线平分第二、四象限角,
∴,
∴,
∴是等腰直角三角形,
∴,
∴,
代入,得,
解得:,
∴,
联立得:,
解得:或,
∴,,
∴,
∵,,
∴四边形是平行四边形,
∵,
∴四边形是矩形,
∴,
答:需要在高速路旁修建隔音屏障的长度是80米.
【点睛】本题主要考查了一次函数和反比例函数的综合应用,两点之间距离公式,矩形的判定和性质,解题的关键是作出辅助线,熟练掌握两点之间距离公式,准确计算.
7.(1)C
(2)和
(3)①;②
【分析】(1)首先根据“不动点”的定义,可知,据此再根据方程的解的性质,即可一一判定;
(2)首先根据“不动点”的定义,可知,据此再解方程,即可求得;
(3)①根据“不动点”的定义,可知,可得方程,再根据该函数图象上有且只有一个“不动点”,利用一元二次方程根的判别式可得,再根据a的范围即可求解;
②首先由,,可求得,据此即可求得该二次函数的顶点坐标,再由(2)可知:双曲线图象上第一象限的“不动点”为,可得抛物线与直线有两个交点,据此即可解答.
【详解】(1)解:A.直线的图象上有无数个“不动点”,故该说法正确,不符合题意;
B.当时,可得,此方程无解,故函数的图象上没有“不动点”, 故该说法正确,不符合题意;
C.当时,可得,此方程无解,故直线的图象上没有“不动点”,故该说法不正确,符合题意;
D.当时,可得,解得,,故函数的图象上有两个“不动点”, 故该说法正确,不符合题意;
故选:C;
(2)解:根据题意得:,
解得或,
故双曲线上的“不动点”为和;
(3)解:①抛物线(、为常数)上有且只有一个“不动点”,
方程组只有一组解,
方程有两个相等的实数根,
,
解得,
,
故的取值范围为;
②,,
,
,
该抛物线的开口向上,顶点坐标为,
由(2)知:双曲线图象上第一象限的“不动点”为,
过双曲线图象上第一象限的“不动点”做平行于轴的直线,且,
抛物线与直线有两个交点,
如图:
抛物线上有四个点到的距离为,
的取值范围为.
【点睛】本题考查二次函数的图象及性质,新定义,一元二次方程根的判别式,熟练掌握二次函数的图象及性质,理解定义,并与二次函数的性质结合解题是关键.
8.(1)见解析
(2)①关于y轴对称;②2;2
(3)③x1=2,x2=0;④或
(4)或1
【分析】(1)先描点,再连线即可得到;
(2)①通过观察图像,可得图像关于轴对称;②利用数形结合的思想进行求解,把方程的解转化为图像之间的交点的横坐标即可求解;
(3)③根据图像的平移的性质即可求解;④通过数形结合的思想进行求解即可;
(4)把交点转化为方程的根,一个交点,即方程只有一个根,需要进行分类讨论.
【详解】(1)解:y=|x|+图像如下:
(2)解:①通过观察图像可得:y=|x|+图像关于轴对称,
故答案为:关于y轴对称;
②如图可知函数图像与直线y=2有2个交点;
即方程|x|+有2个实数根;
故答案为:2,2;
(3)解:③方程的|x-1|+-2=0的解为方程|x|+的解x1=1,x2=-1向右平移一个单位,得x1=2,x2=0,
④当|x|+-,由图像可得解为:,
不等式|x|+-<0的解集为:或;
故答案为:x1=2,x2=0;或;
(4)解:当x>0时,直线y=kx+3与y=|x|+只有一个交点,
即只有一个根,
,
,
当时,解得;
当时,是一元二次方程,
,
即,
解得:,
综上:k的值为或1时,直线y=kx+3与y=|x|+只有一个交点.
【点睛】题考查了反比例函数的图像和性质、画函数图象、方程的根、不等式的解集、函数图象的平移,解题的关键是理解题意,运用数形结合的思想进行求解.
9.;(1),3,4,0,1,;(2)见解析;(3)①(﹣2,2),②2,③增大;高,2
【分析】[建模]依据平均数的算法,可得y与x的关系式;
(1)利用函数关系式,根据自变量x的值,即可得到y的值;
(2)依据坐标,进行描点、连线,即可得到函数图象;
(3)①由函数图象可得对称中心的坐标;
②依据函数图象与直线y=2无限接近,即可得出该函数值y不可能等于2;
③依据函数图象的增减性,即可得出y随x的增大而增大.
[应用]依据函数图象的增减性,即可得到y随x的增大而增大,函数值y与2无限接近.
【详解】解:[建模]由题意得:y与x的关系式为,
故答案为:;
(1)当x=﹣4时,y=;
当x=﹣3时,y=3;
当x=﹣时,y=4;
当x=﹣时,y=0;
当x=﹣1时,y=1;
当x=0时,y=;
故答案为:;3;4;0;1;;
(2)如图所示:
(3)①由函数图象可得,对称中心是(﹣2,2);
②函数图象与直线y=2无限接近,故该函数值y不可能等于2;
③由函数图象可得,当x>﹣2时,函数图象从左往右上升,即y随x的增大而增大.
故答案为:①(﹣2,2);②2;③增大;
[应用]由函数图象可得,当x≥0时,函数图象从左往右上升,与直线y=2无限接近,即y随x的增大而增大,函数值y与2无限接近,
故粽形香囊越多,所购买物品的平均价格越高,但不会突破2元.
故答案为:高,2.
【点睛】本题主要考查了反比例函数的图象和性质,利用图象解决问题,从图上获取有用的信息是解题的关键所在.还能利用图象直接比较函数值或是自变量的大小.将数形结合在一起是分析解决函数问题的一种常用方法.
10.(1)6
(2)①2.5,2;②见解析
(3)①减小;②上,1
【分析】(1)根据,,关联两个等式计算即可求解;
(2)①将,分别代入计算即可求解;②根据题(2)①表格数据,先描出各点,顺次连接各点即可画出所求函数图象;
(3)①根据题(2)②所求图象特征即可得到结论;②根据反比例函数平移规律即可求解.
【详解】(1)∵并联电路,,
∴,即,
故答案为:6;
(2)①当时,,即,
当时,,即,
故答案为:2.5,2;
②如图所示:
先描出点(3,3),(4,2.5),(5,2.2),(6,2),再顺次连接这些点即可画出所求函数图象,
(3)①由题(2)②所求图象可知,是减函数,其函数值随R的增大而减小,
故答案为:减小;
②根据反比例函数平移规律可得:向上平移1个单位可得:,
故答案为:上,1.
【点睛】本题考查函数图象,涉及到画函数图象、函数的性质,解题的关键是掌握函数的研究方法:列表、描点、连线画函数图象,再利用数形结合的思想理解函数的性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年12月5日初三数学作业
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.(2023上·广东深圳·九年级深圳市高级中学校考期中)建筑是一门不断演化和创新的艺术,从古代的大理石殿堂到现代的钢铁森林,它的魅力在于其无限的可能性.近年来,一种名为双曲铝单板的新兴材料以其独特的曲线和光泽,为建筑注入了新的时尚元素,同时也赋予了建筑更多的创意和流动性.
图2为某广东厂家设计制造的双曲铝单板建筑的横截面,可以看作由两条曲线、(反比例函数图像的一支)和若干线段围成,其中四边形与四边形均为矩形,,,,,,如图2所示,取中点,以点为原点,所在直线为轴建立平面直角坐标系.
请回答下列问题:
(1)如图2,求所在双曲线的解析式;
(2)如图3,为在曲面实现自动化操作,工程师安装了支架,并加装了始终垂直于的伸缩机械臂用来雕刻所在曲面的花纹,请问点在上滑动过程中,最长为多少米?
(3)如图4,为通风透气避免潮湿,在某一时刻,打开遮光板,太阳光线经点恰好照射到点,请求出此时线段上光线无法直射部分即线段的长.
2.(2022上·广东深圳·九年级校考期中)小亮在学习了反比例函数的图象和性质后,进一步研究了函数的图象与性质.他利用描点法在给出的平面直角坐标系中画出函数的图象的一部分,并解答下列问题.
(1)______,______,并在图中补全函数的图象.
(2)根据以上探究结果,完成下列问题:
①函数,自变量的取值范围为______;
②函数的图象是______图形填中心对称或轴对称;
③直接写出当时,自变量的值______.
(3)求出当一次函数与函数图象交点个数不少于两个时,的取值范围是______.
3.(2021上·河南新乡·九年级统考期末)某同学根据学习函数的经验,探究了函数y=||+1的图象和性质,下面是他的探究过程,请补充完整:
(1)写出函数y=||+1的自变量的取值范围是 ;
(2)如表是函数y与自变量x的几组对应值:则m= ,n= ;
x … ﹣3 ﹣2 ﹣1 0 1 3 4 5 6 7 …
y … 1.6 m 2 2.5 4 n 2.5 2 1.75 1.6 …
(3)在如图所示的平面直角坐标系xOy中,已画出函数图象的一部分,请补全此函数的图象;
(4)进一步探究函数图象发现:
①函数y=||+1的图象是轴对称图形,对称轴是直线 ;当x满足 时,y随x的增大而减小;
②方程||+1=4的解为 .
4.(2023·广东深圳·校考模拟预测)阅读材料:“三等分角”是数学史上一个著名问题.今天人们已经知道,仅用圆规和直尺是不可能作出的.在研究这个问题的过程中,数学家帕普斯借助函数给出了一种“三等分锐角”的方法,如图1,步骤如下:
①建立直角坐标系,将已知锐角的顶点与原点O重合,角的一边与x轴正方向重合;
②在直角坐标系中,绘制函数的图象,图象与已知角的另一边交于点P;
③以P为圆心、以为半径作弧,交函数的图象于点R;
④分别过点P和R作x轴和y轴的平行线,分别交于点M,点Q;
⑤连接,得到.则.
思考问题:
(1)设,,求直线的函数解析式(用含a,b的代数式表示),并说明Q点在直线上;
(2)证明:.
(3)如图2,若直线与反比例函数交于点C,D为反比例函数第一象限上的一个动点,使得.求用材料中的方法求出满足条件D点坐标.
5.(2023·广东深圳·校考三模)【综合实践】
如图所示,是《天工开物》中记载的三千多年前中国古人利用桔槔在井上汲水的情境(杠杆原理:阻力阻力臂动力动力臂,如图,即),受桔槔的启发,小杰组装了如图所示的装置.其中,杠杆可绕支点O在竖直平面内转动,支点O距左端,距右端,在杠杆左端悬挂重力为的物体A.
(1)若在杠杆右端挂重物B,杠杆在水平位置平衡时,重物B所受拉力为______.
(2)为了让装置有更多的使用空间,小杰准备调整装置,当重物B的质量变化时,的长度随之变化.设重物B的质量为,的长度为.则①y关于x的函数解析式是______.
②完成下表:
… 10 20 30 40 50 …
… 8 a 2 b …
③在直角坐标系中画出该函数的图象.
(3)在(2)的条件下,将函数图象向右平移4个单位长度,与原来的图像组成一个新的函数图象,记为L.若点A的坐标为,在L上存在点Q,使得.请直接写出所有满足条件的点Q的坐标.
6.(2023·广东深圳·校考一模)【定义】在平面内,把一个图形上任意一点与另一个图形上任意一点之间的距离的最小值,称为这两个图形之间的距离,即A,B分别是图形M和图形N上任意一点,当的长最小时,称这个最小值为图形M与图形N之间的距离.
例如,如图1,,线段的长度称为点A与直线之间的距离,当时,线段的长度也是与之间的距离.
【应用】
(1)如图2,在等腰中,,,点D为边上一点,过点D作交于点E.若,,则与之间的距离是 ;
(2)如图3,已知直线与双曲线交于与B两点,点A与点B之间的距离是 ,点O与双曲线之间的距离是 ;
【拓展】
(3)按规定,住宅小区的外延到高速路的距离不超过时,需要在高速路旁修建与高速路相同走向的隔音屏障(如图4).有一条“东南 西北”走向的笔直高速路,路旁某住宅小区建筑外延呈双曲线的形状,它们之间的距离小于.现以高速路上某一合适位置为坐标原点,建立如图5所示的直角坐标系,此时高速路所在直线的函数表达式为,小区外延所在双曲线的函数表达式为,那么需要在高速路旁修建隔音屏障的长度是多少?
7.(2023下·广东深圳·九年级校联考阶段练习)在平面直角坐标系中,如果一个点的横坐标与纵坐标相等,则称该点为“不动点”
例如、、都是“不动点”,已知双曲线
(1)下列说法不正确的是( )
A.直线的图象上有无数个“不动点”
B.函数的图象上没有“不动点”
C.直线的图象上有无数个“不动点”
D.函数的图象上有两个“不动点”
(2)求双曲线上的“不动点”;
(3)若抛物线(、为常数)上有且只有一个“不动点”,
①当时,求的取值范围.
②如果,过双曲线图象上第一象限的“不动点”作平行于轴的直线,若抛物线上有四个点到的距离为,直接写出的取值范围.
8.(2022·广东深圳·深圳市宝安中学(集团)校考三模)y=x+是一种类似于反比例函数的对勾函数,形如y=ax+.其函数图像形状酷似双勾,故称“对勾函数”,也称“勾勾函数”、“海鸥函数”.y=x+函数图像如下图所示.根据y=x+图像对函数y=|x|+的图像和性质进行了探究.
(1)绘制函数图像:y=|x|+
列表:下表是x与y的几组对应值
x ……… -3 -2 -1 - - 1 2 3 ………
y ……… 2 2 ………
描点:根据表中各组对应值,在平面直角坐标系中描出各点;
连线:用平滑的曲线顺次连接各点,请你在平面直角坐标系中将y=|x|+图像补充完整;
(2)观察发现:
①写出函数y=|x|+的一条性质_________
②函数图像与直线y=2有_________个交点,
所以对应的方程|x|+有_________个实数根.
(3)分析思考:
③方程的|x-1|+-2=0的解为_________
④不等式|x|+-<0,x的取值范围为_________
(4)延伸探究:
⑤当x>0时,直线y=kx+3与y=|x|+只有一个交点,求k的值?
9.(2022·广东深圳·模拟预测)【建模】某班开端午联欢会,生活委员彤彤先购买了2个装饰挂件共计3元,又购买了单价为2元的粽形香囊x个,设y(元)是所有装饰挂件和粽形香囊的平均价格,则y与x的关系式为 .
【探究】根据函数的概念,彤彤发现:y是x的函数.结合自己学习函数的经验,为了更好地研究这个函数,彤彤打算先脱离实际背景,对该函数的完整图象与性质展开探究.请根据所给信息,将彤彤的探究过程补充完整:
(1)列表:
x … ﹣4 ﹣3 ﹣1 0 …
y … …
(2)在平面直角坐标系中描点、连线,画出该函数图象:
(3)观察图象,彤彤发现以下性质:
①该函数图象是中心对称图形,对称中心是 ;
②该函数值y不可能等于 ;
③当x>﹣2时,y随x的增大而 (填“增大”或者“减小”),当x<﹣2时,亦是如此.
【应用】根据上述探究,结合实际经验,彤彤得到结论:粽形香囊越多,所购买物品的平均价格越 (填“高”或者“低”),但不会突破 元.
10.(2022·广东深圳·统考二模)在并联电路中,电源电压为,小亮根据“并联电路分流不分压”的原理知道:(,).已知R1为定值电阻,当R变化时,干路电流也会发生变化,且干路电流与R之间满足如下关系:.
(1)定值电阻的阻值为__________;
(2)小亮根据学习函数的经验,参照研究函数的过程与方法,对比反比例函数来探究函数的图象与性质.
①列表:下表列出点与R的几组对应值,请写出m,n的值:__________,__________;
R … 3 4 5 6 …
… 2 1.5 1.2 1 …
… 3 m 2.2 n …
②描点、连线:在平面直角坐标系中,以①给出的R的取值为横坐标,以相对应的值为纵坐标,描出相应的点,并将各点用光滑曲线顺次连接起来;
(3)观察图象并分析表格,回答下列问题:
①随R的增大而__________;(填“增大”或“减小”)
②函数的图象是由的图象向__________平移__________个单位而得到.
参考答案:
1.(1);
(2)
(3)8
【分析】(1)根据题意可得,再利用待定系数法解答,即可求解;
(2)先求出所在直线解析式为,再根据反比例函数图像轴对称的性质,可得曲线关于直线轴对称,然后联立,即可求解;
(3)先求出所在直线解析式为,再根据,可设直线解析式为,然后,整理得:,利用一元二次方程根的判别式,可得,从而得到,进而得到解析式为,即可求解.
【详解】(1)解:,,,为中点,,
,
设所在双曲线的表达式为,
将点坐标代入表达式中,得:
解得:,
抛物线表达式为;
(2)解:根据题意得:点与点坐标分别为,,
设所在直线解析式为,
将、两点坐标代入得:,
解得,,
所在直线解析式为,
根据反比例函数图像轴对称的性质,曲线关于直线轴对称,
联立,解得,
联立,解得,
,
(3)解:如图,光线与曲线只有一个交点,
设直线的解析式为,
将点,点代入得:,
解得,,
所在直线解析式为,
∵,
可设直线解析式为,
∴,
整理得:
∴
解得:,(舍去),
解析式为,
将分别代入,
解得:,
∴点,点,点点,
.
【点睛】本题主要查了反比例函数的实际应用,一元二次方程根的判别式,利用数形结合思想解答是解题的关键.
2.(1),,图见解析
(2)①;②轴对称;③或
(3)
【分析】(1)利用函数解析式分别求出对应的函数值,利用描点法画出图象即可.
(2)观察图象即可得到结论.
(3)利用图象即可解决问题.
【详解】(1)把,代入得,把代入得,
,.
故答案为:,.
画出函数的图象如图所示,
;
(2)观察函数图象,
函数,自变量的取值范围为;
函数的图象是轴对称图形填中心对称或轴对称;
当时,自变量的值是或
故答案为:,轴对称,或.
(3)如图,
当直线过时,函数的图象与函数的图象有两个交点,此时,
由图象可知,当时,函数的图象与函数的图象交点个数不少于两个,
故答案为:.
【点睛】本题是反比例函数与一次函数的交点问题,考查反比例函数的图象与性质,数形结合是解题的关键.
3.(1)x≠2;(2), 4;(3)见解析;(4)①x=2,x>2;②x1=1,x2=3.
【分析】(1)分母不为零;
(2)把x=-2和3分别代入y=||+1即可求得;
(3)画出函数图象即可;
(4)根据图象得出结论.
【详解】解:(1)函数y=||+1的自变量x的取值范围是:x≠2;
(2)把x=﹣2和3分别代入y=||+1得,m=+1=,n=3+1=4,
故答案为,4;
(3)如图所示;
(4)由图象发现:①函数y=||+1的图象是轴对称图形,对称轴是直线x=2;当x满足x>2时,y随x的增大而减小;
故答案为x=2,x>2;
②方程||+1=4的解为x1=1,x2=3,
故答案为x1=1,x2=3.
【点睛】此题考查了反比例函数图象和性质,涉及的知识有:自变量的取值范围、画图象、熟练掌握数形结合的思想是解本题的关键.
4.(1),证明见解析
(2)见解析
(3)或
【分析】(1)由轴,轴,,,即可得出M点的坐标,即可,再将点Q的坐标代入解析式即可判断点Q是否在直线上;
(2)连接,交于点S,由矩形的性质和平行线的性质即可得到结论;
(3)先求出点,可得,然后分两种情况讨论:当D点在下方时,当D点在上方时,即可求解.
【详解】(1)解:设直线的函数表达式为,
由题意得:,
∴四边形为矩形,
∵,,
∴,,
把点代入得:,
∴直线的函数表达式为,
∵的坐标满足,
∴点Q在直线上;
(2)解:连接,交于点S,
由题意得四边形是矩形,
∴,,,
∴,
∴,
∴
∵,
∴.
∴,
∵轴,
∴,
∴,即.
(3)解:∵直线与反比例函数交于点C,
∴,解得:或(舍去),
∴,
∴,
当D点在下方时,如图,以C为圆心,为半径画弧,交反比例函数于点E,作轴,作轴,连接并延长交反比例与点F,作,连接,与交于点H,,,,
作于I,则,,,
,
则,,
即,
同理,当D点在上方时,有.
【点睛】此题在考查三等分角的作法时,综合考查了待定系数法求函数解析式的方法、矩形的性质以及三角形外角的性质等,综合性较强.
5.(1)
(2)①;②见解析;③见解析
(3)或
【分析】(1)根据公式进行计算即可;
(2)①根据公式即可得到;②根据(2)①所求求出a、b的值即可;③先描点,再连线,画出函数图象即可;
(3)先根据面积求出点Q的纵坐标,再根据反比例函数性质和平移的性质求出点Q的坐标即可.
【详解】(1)解:∵,
∴
∴重物B所受拉力为,
故答案为:;
(2)解:①∵,
∴,即,
故答案为:;
②由(2)①得,
填表如下:
… 10 20 30 40 50 …
… 8 4 2 …
③函数图象如下所示:
(3)解:∵点A的坐标为,
∴,
∵,
∴,
∴,
在中,当时,
∴在函数上满足题意的Q的坐标为,
∵将函数图象向右平移4个单位长度,与原来的图像组成一个新的函数图象,记为L,
∴点,即也在L上,即满足题意的Q的坐标为;
综上所述,点Q的坐标为或.
【点睛】本题主要考查了反比例函数的实际运用,正确理解题意是解题的关键.
6.(1);(2),;(3)80米
【分析】(1)过点D作于点H,得出是等腰直角三角形,根据等腰直角三角形的性质求出结果即可;
(2)先根据一次函数解析式求出,然后再求出反比例函数解析式,再求出点,根据两点点距离公式求出的值即可;作,且与双曲线只有一个交点,设直线的解析式为,求出一次函数解析式,再求出交点坐标,最后求出的值即可;
(3)作直线,设的解析式为,与双曲线交于点A、B,过点O作于点P,过点P作轴于点H,过点A、B分别作直线的垂线、,垂足为E、F,先求出直线的解析式,然后求出点A、B的坐标,根据两点之间距离公式求出的长,进而即可得出答案.
【详解】解:(1)如图,过点D作于点H,
∵,,
∴,
∵,
∴是等腰直角三角形,
∴,
∵,,
∴,
∴;
故答案为:;
(2)把代入中,得:,
∴,
把代入,得:,
∴,
∴双曲线的解析式为,
联立,得:,
即,
解得:,,
∴,
∴;
如图,作,且与双曲线只有一个交点,设直线的解析式为,
则,
整理得:,
∴,
∴或(不符合题意,舍去),
∴直线的解析式为,
由,
解得:,
∴,
∴;
故答案为:;.
(3)如图,作直线,设的解析式为,与双曲线交于点A、B,过点O作于点P,过点P作轴于点H,过点A、B分别作直线的垂线、,垂足为E、F,
则,
∵直线平分第二、四象限角,
∴,
∴,
∴是等腰直角三角形,
∴,
∴,
代入,得,
解得:,
∴,
联立得:,
解得:或,
∴,,
∴,
∵,,
∴四边形是平行四边形,
∵,
∴四边形是矩形,
∴,
答:需要在高速路旁修建隔音屏障的长度是80米.
【点睛】本题主要考查了一次函数和反比例函数的综合应用,两点之间距离公式,矩形的判定和性质,解题的关键是作出辅助线,熟练掌握两点之间距离公式,准确计算.
7.(1)C
(2)和
(3)①;②
【分析】(1)首先根据“不动点”的定义,可知,据此再根据方程的解的性质,即可一一判定;
(2)首先根据“不动点”的定义,可知,据此再解方程,即可求得;
(3)①根据“不动点”的定义,可知,可得方程,再根据该函数图象上有且只有一个“不动点”,利用一元二次方程根的判别式可得,再根据a的范围即可求解;
②首先由,,可求得,据此即可求得该二次函数的顶点坐标,再由(2)可知:双曲线图象上第一象限的“不动点”为,可得抛物线与直线有两个交点,据此即可解答.
【详解】(1)解:A.直线的图象上有无数个“不动点”,故该说法正确,不符合题意;
B.当时,可得,此方程无解,故函数的图象上没有“不动点”, 故该说法正确,不符合题意;
C.当时,可得,此方程无解,故直线的图象上没有“不动点”,故该说法不正确,符合题意;
D.当时,可得,解得,,故函数的图象上有两个“不动点”, 故该说法正确,不符合题意;
故选:C;
(2)解:根据题意得:,
解得或,
故双曲线上的“不动点”为和;
(3)解:①抛物线(、为常数)上有且只有一个“不动点”,
方程组只有一组解,
方程有两个相等的实数根,
,
解得,
,
故的取值范围为;
②,,
,
,
该抛物线的开口向上,顶点坐标为,
由(2)知:双曲线图象上第一象限的“不动点”为,
过双曲线图象上第一象限的“不动点”做平行于轴的直线,且,
抛物线与直线有两个交点,
如图:
抛物线上有四个点到的距离为,
的取值范围为.
【点睛】本题考查二次函数的图象及性质,新定义,一元二次方程根的判别式,熟练掌握二次函数的图象及性质,理解定义,并与二次函数的性质结合解题是关键.
8.(1)见解析
(2)①关于y轴对称;②2;2
(3)③x1=2,x2=0;④或
(4)或1
【分析】(1)先描点,再连线即可得到;
(2)①通过观察图像,可得图像关于轴对称;②利用数形结合的思想进行求解,把方程的解转化为图像之间的交点的横坐标即可求解;
(3)③根据图像的平移的性质即可求解;④通过数形结合的思想进行求解即可;
(4)把交点转化为方程的根,一个交点,即方程只有一个根,需要进行分类讨论.
【详解】(1)解:y=|x|+图像如下:
(2)解:①通过观察图像可得:y=|x|+图像关于轴对称,
故答案为:关于y轴对称;
②如图可知函数图像与直线y=2有2个交点;
即方程|x|+有2个实数根;
故答案为:2,2;
(3)解:③方程的|x-1|+-2=0的解为方程|x|+的解x1=1,x2=-1向右平移一个单位,得x1=2,x2=0,
④当|x|+-,由图像可得解为:,
不等式|x|+-<0的解集为:或;
故答案为:x1=2,x2=0;或;
(4)解:当x>0时,直线y=kx+3与y=|x|+只有一个交点,
即只有一个根,
,
,
当时,解得;
当时,是一元二次方程,
,
即,
解得:,
综上:k的值为或1时,直线y=kx+3与y=|x|+只有一个交点.
【点睛】题考查了反比例函数的图像和性质、画函数图象、方程的根、不等式的解集、函数图象的平移,解题的关键是理解题意,运用数形结合的思想进行求解.
9.;(1),3,4,0,1,;(2)见解析;(3)①(﹣2,2),②2,③增大;高,2
【分析】[建模]依据平均数的算法,可得y与x的关系式;
(1)利用函数关系式,根据自变量x的值,即可得到y的值;
(2)依据坐标,进行描点、连线,即可得到函数图象;
(3)①由函数图象可得对称中心的坐标;
②依据函数图象与直线y=2无限接近,即可得出该函数值y不可能等于2;
③依据函数图象的增减性,即可得出y随x的增大而增大.
[应用]依据函数图象的增减性,即可得到y随x的增大而增大,函数值y与2无限接近.
【详解】解:[建模]由题意得:y与x的关系式为,
故答案为:;
(1)当x=﹣4时,y=;
当x=﹣3时,y=3;
当x=﹣时,y=4;
当x=﹣时,y=0;
当x=﹣1时,y=1;
当x=0时,y=;
故答案为:;3;4;0;1;;
(2)如图所示:
(3)①由函数图象可得,对称中心是(﹣2,2);
②函数图象与直线y=2无限接近,故该函数值y不可能等于2;
③由函数图象可得,当x>﹣2时,函数图象从左往右上升,即y随x的增大而增大.
故答案为:①(﹣2,2);②2;③增大;
[应用]由函数图象可得,当x≥0时,函数图象从左往右上升,与直线y=2无限接近,即y随x的增大而增大,函数值y与2无限接近,
故粽形香囊越多,所购买物品的平均价格越高,但不会突破2元.
故答案为:高,2.
【点睛】本题主要考查了反比例函数的图象和性质,利用图象解决问题,从图上获取有用的信息是解题的关键所在.还能利用图象直接比较函数值或是自变量的大小.将数形结合在一起是分析解决函数问题的一种常用方法.
10.(1)6
(2)①2.5,2;②见解析
(3)①减小;②上,1
【分析】(1)根据,,关联两个等式计算即可求解;
(2)①将,分别代入计算即可求解;②根据题(2)①表格数据,先描出各点,顺次连接各点即可画出所求函数图象;
(3)①根据题(2)②所求图象特征即可得到结论;②根据反比例函数平移规律即可求解.
【详解】(1)∵并联电路,,
∴,即,
故答案为:6;
(2)①当时,,即,
当时,,即,
故答案为:2.5,2;
②如图所示:
先描出点(3,3),(4,2.5),(5,2.2),(6,2),再顺次连接这些点即可画出所求函数图象,
(3)①由题(2)②所求图象可知,是减函数,其函数值随R的增大而减小,
故答案为:减小;
②根据反比例函数平移规律可得:向上平移1个单位可得:,
故答案为:上,1.
【点睛】本题考查函数图象,涉及到画函数图象、函数的性质,解题的关键是掌握函数的研究方法:列表、描点、连线画函数图象,再利用数形结合的思想理解函数的性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
