物理人教版(2019)选择性必修第一册4.1光的折射(共35张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册4.1光的折射(共35张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 38.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-06 00:00:00 | ||
图片预览







文档简介
(共35张PPT)
4.1 光的折射
物理人教版(新教材)选择性必修第一册
光射到水面发生了什么?
界面
入射光线
反射光线
法线
入射角
反射角
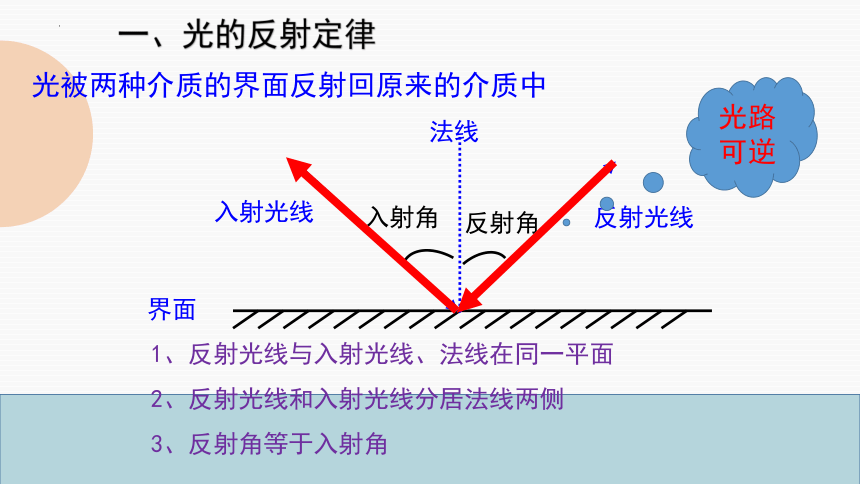
光被两种介质的界面反射回原来的介质中
一、光的反射定律
1、反射光线与入射光线、法线在同一平面
2、反射光线和入射光线分居法线两侧
3、反射角等于入射角
光路可逆
二、光的折射定律
1、折射光线、入射光线、法线在同一平面内
2、折射光线和入射光线分居法线两侧
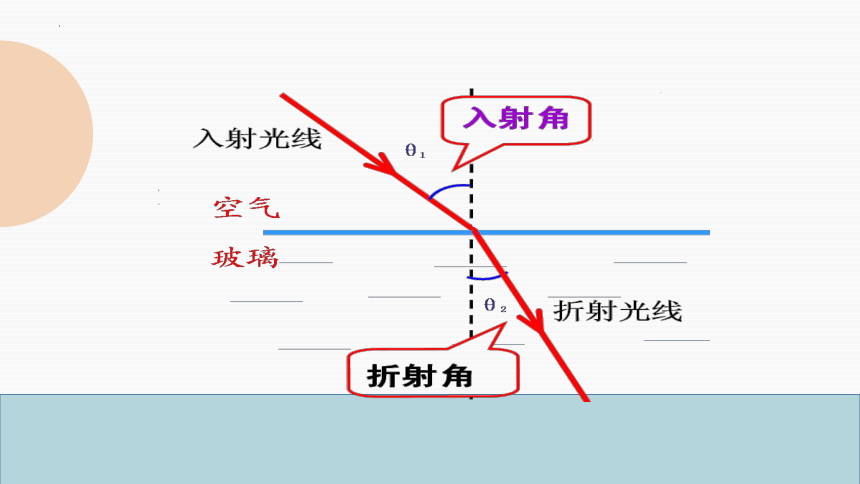
折射角、入射角有什么关系呢 ?
θ1
θ2
空气
玻璃
N
N'
A
O
B
3、当光从空气斜射入玻璃中时,折射角小于入射角
玻璃
4、当光从玻璃斜射入空气中时,折射角大于入射角
空气
水
玻璃
5、当入射角增大时,折射角也随着增大
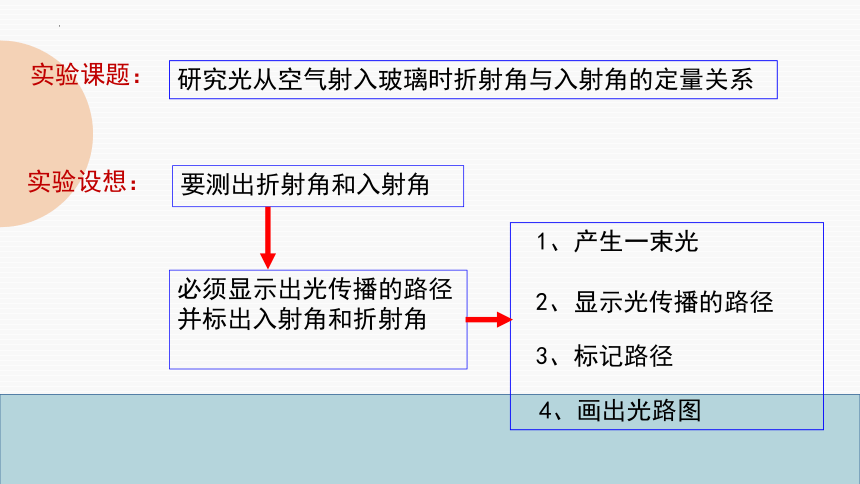
实验课题:
研究光从空气射入玻璃时折射角与入射角的定量关系
实验设想:
要测出折射角和入射角
必须显示出光传播的路径并标出入射角和折射角
1、产生一束光
2、显示光传播的路径
3、标记路径
4、画出光路图
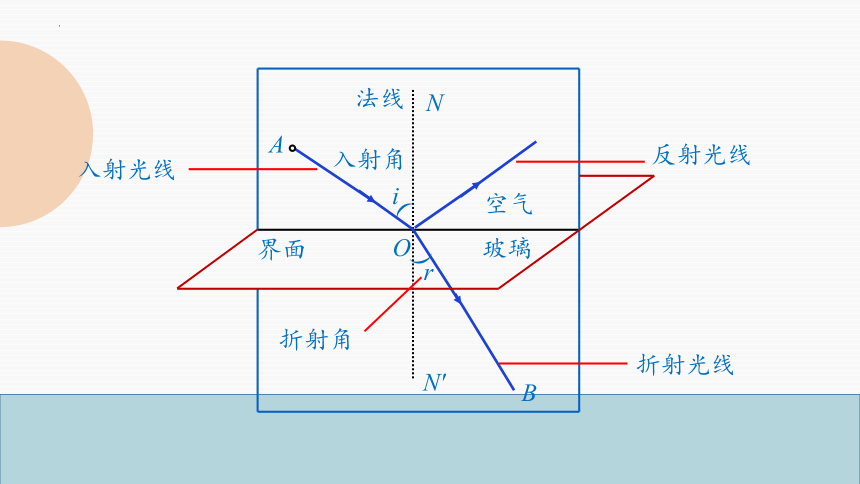
光的折射现象
N
N′
空气
玻璃
i
r
O
A
B
界面
法线
入射光线
折射光线
入射角
折射角
(
(
反射光线
光的折射规律
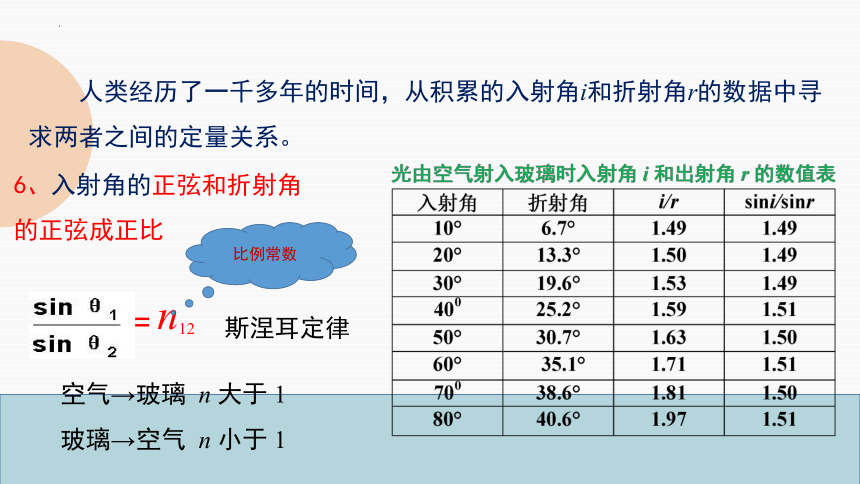
人类经历了一千多年的时间,从积累的入射角i和折射角r的数据中寻求两者之间的定量关系。
6、入射角的正弦和折射角的正弦成正比
=
n12
比例常数
空气→玻璃 n 大于 1
玻璃→空气 n 小于 1
斯涅耳定律
1、规律得出的过程:
2、正确规律的得出往往要经过曲折的过程,要经过实践的多次检验。
自主感悟
古希腊哲学家托勒密的结论:折射角与入射角成正比
荷兰数学家斯涅耳的结论:
折射角与入射角的正弦成正比
托勒密的实验数据记录非常详细、准确,只可惜欠缺数学眼光,致使结论的总结出现错误。而这个看来仅仅一步之遥的距离却又使人类经历了一千五百多年的探索!
7、折射率
(1)折射率-----是光从真空射入某种介质中时的折射率(光从真空射入某种介质时的折射率,叫做该种介质的绝对折射率,也简称为某种介质的折射率.相对折射率在高中不作要求 )
(2)n的大小与介质有关,与θ1和θ2无关,对于确定的介质,n是定值,不能说n∝sinθ1或n∝1/sinθ2
(3)折射率无单位,任何介质的折射率皆大于1。
定义式:
折射率
灵机一动
θ1
θ2
光很有可能是一种波
这跟惠更斯原理揭示的波折射的规律何其相似
光的反射、折射、干涉、衍射、多普勒效应等波动特征在以后的学习中会一一碰到
光确实是一种波
某介质的折射率,等于光在真空中的速度c与光在介质中的速度v之比:
c
v
n=
(n>1)
光在不同介质中的速度不同,这正是发生折射的原因。
研究表明:
折射光路也是可逆的吗?
i
r
空气
水
折射光路是可逆的
[自我检测]
1.正误判断
(1)光从一种介质进入另一种介质时传播方向就会变化。( )
解析 如果光垂直分界面入射时,光的传播方向就不会变化。
答案 ×
(2)介质的密度越大,其折射率一定也越大。( )
解析 介质的折射率与介质的密度没有必然联系,密度大,其折射率不一定大。
答案 ×
(3)光从真空斜射入任何介质时,入射角均大于折射角。( )
答案 √
(4)折射定律是确定折射光线位置的规律。( )
答案 √
(5)光的折射率随入射角增大而增大。( )
答案 ×
例1.(多选)关于光的反射与折射,下列说法正确的是( )
A.光发生反射时,光的传播方向不一定改变
B.光发生反射时,光的传播方向可能偏转90°
C.光发生反射时,光的传播方向一定改变
D.光发生折射时,一定伴随着反射现象
解析 光发生反射时,光的传播方向一定发生改变,且可以改变90°,A项错,B、C两项对;发生折射时,一定伴随着反射现象,但有反射现象,不一定有折射现象,D项对。
答案 BCD
实验:测定玻璃的折射率
三、实验器材
长方形玻璃砖、白纸、木板、大头针、图钉、量角器、三角板(或直尺)、铅笔。
一、实验目的
测定玻璃的折射率。
二、实验原理
用插针法确定光路,找出跟入射光线相对应的出射光线,用量角器测入射角θ1和折射角θ2,根据折射定律计算出玻璃的折射率 。
四、实验步骤
1.用图钉把白纸固定在木板上.
2.在白纸上画一条直线aa′,并取aa′上的一点O为入射点,作过O的法线NN′.
3.画出线段AO作为入射光线,并在AO上插上P1、P2两根大头针.
4.在白纸上放上玻璃砖,使玻璃砖的一条长边与直线aa′对齐,并画出另一条长边的对齐线bb′.
5.眼睛在bb′的一侧透过玻璃砖观察两个大头针并调整视线方向,使P1的像被P2的像挡住,然后在眼睛这一侧插上大头针P3,使P3挡住P1、P2的像,再插上P4,使P4挡住P3和P1、P2的像.
6.移去玻璃砖,拔去大头针,由大头针P3、P4的针孔位置确定出射光线O′B及出射点O′,连接O、O′得线段OO′.
7.用量角器测量入射角θ1和折射角θ2,并查出其正弦值sin θ1和sin θ2.
8.改变入射角,重复实验,算出不同入射角时的,并取平均值.
五、数据处理
1.平均值法
算出不同入射角时的比值 ,最后求出在几次实验中所测的 平均值,即为玻璃砖的折射率。
2.图象法
以sin θ1值为横坐标、以sinθ2值为纵坐标,建立直角坐标系,如图1所示。描数据点,过数据点连线得一条过原点的直线。求解图线斜
率k,则 ,故玻璃砖折射率 。
3.作图法
在找到入射光线和折射光线以后,以入射点O为圆心,以任意长为半径画圆,分别与AO交于C点、OO′(或OO′的延长线)交于D点,过C、D两点分别向NN′作垂线,交NN′于C′、D′,用直尺量出CC′和DD′的长,如图 2所示。由于 , ,且CO=DO,所以折射率 。
六、注意事项
(1)实验时,尽可能将大头针竖直插在纸上,且P1和P2之间,P2与O点之间,P3与P4之间,P3与O′点之间距离要稍大一些。
(2)入射角θ1应适当大一些,以减小测量角度的误差,但入射角不宜太大,也不宜太小。
(3)在操作时,手不能触摸玻璃砖的光洁面。更不能把玻璃砖界面当尺子画界线。
(4)在实验过程中,玻璃砖与白纸的相对位置不能改变。
(5)玻璃砖应选用宽度较大的,宜在5 cm以上。若宽度太小,则测量误差较大。
七、误差分析
(1)入射光线和出射光线确定得不够精确,因此要求插大头针时,两大头针间距应适当大一些。
(2)入射角和折射角的测量造成误差,故入射角应适当大些,以减小测量的相对误差。
1.关于介质的折射率,下列说法正确的是( )
A.由折射率的公式 可知,介质的折射率与入射角θ1的正弦成正比
B.由折射率公式 可知,介质折射率与光在介质中的传播速度v成反比
C.折射率反映的是介质本身的光学性质由介质本身及光的性质共同决定
D.玻璃的折射率大于1,水的折射率小于1
B
2.如图所示是光线以相同的入射角从空气射入三种不同介质时的折射情况,则在三种介质中光的传播速度最小的是( )
A.介质甲 B.介质乙 C.介质丙 D.三种介质均一样
C
3.如图所示,光在真空和某介质界面MN上发生折射,由图可知( )
A.光是从真空射入介质的
B.光是由介质射入真空的
C.介质的折射率为
D.介质的折射率为
B
4.一条光线以40°的入射角从真空中射到平板透明材料上,光的一部分被反射,一部分被折射,折射光线与反射光线的夹角可能( )
A.小于40°
B.在50°~100°之间
C.在100°~140°之间
D.大于140°
C
5.如图所示,用插针法测定玻璃砖折射率的实验中,下列说法中正确的是( )
A.若P1、P2的距离较大时,通过玻璃砖会看不到P1、P2的像
B.为减少测量误差,P1、P2的连线与法线NN'的夹角应尽量小些
C.为了减小作图误差,P3和P4的距离应适当取大些
D.若P1、P2的连线与法线NN'夹角较大时,有可能在bb′面发生全反射
C
6.如图所示,单色光沿AO从空气射入水中,以O点为圆心,作两半径分别为R和r(R>r)的同心圆,大圆与入射光线相交于A,与折射光线相交于B,小圆与AO延长线相交于M,BM连线恰好和水平界面垂直,垂足为N,则下列说法正确的是( )
A.水的折射率
B.光线从空气中进入水中,频率变大了
C.光线在AO段的传播时间tAO的大于在OB段的传播时间tOB
D.由于数据不足,无法确定入射角和折射角的大小,故无法计算折射率
D
7.某同学做测定玻璃折射率实验时,用他测得的多组入射角θ1与折射角θ2作出sinθ1-sinθ2图像,如图所示,则下列判断正确的是( )
A.他做实验时,研究的是光从空气射入玻璃的折射现象
B.玻璃的折射率为0.67
C.玻璃的折射率为1.5
D.他做实验时,研究的是光从玻璃射入空气的折射现象
AC
8.光从某介质射入空气,入射角θ1从零开始增大到某一值的过程中,折射角θ2也随之增大,则下列说法正确的是( )
A.比值 不变
B.比值不变
C.比值 是一个大于1的常数
D.比值 是一个小于1的常数
BD
4.1 光的折射
物理人教版(新教材)选择性必修第一册
光射到水面发生了什么?
界面
入射光线
反射光线
法线
入射角
反射角
光被两种介质的界面反射回原来的介质中
一、光的反射定律
1、反射光线与入射光线、法线在同一平面
2、反射光线和入射光线分居法线两侧
3、反射角等于入射角
光路可逆
二、光的折射定律
1、折射光线、入射光线、法线在同一平面内
2、折射光线和入射光线分居法线两侧
折射角、入射角有什么关系呢 ?
θ1
θ2
空气
玻璃
N
N'
A
O
B
3、当光从空气斜射入玻璃中时,折射角小于入射角
玻璃
4、当光从玻璃斜射入空气中时,折射角大于入射角
空气
水
玻璃
5、当入射角增大时,折射角也随着增大
实验课题:
研究光从空气射入玻璃时折射角与入射角的定量关系
实验设想:
要测出折射角和入射角
必须显示出光传播的路径并标出入射角和折射角
1、产生一束光
2、显示光传播的路径
3、标记路径
4、画出光路图
光的折射现象
N
N′
空气
玻璃
i
r
O
A
B
界面
法线
入射光线
折射光线
入射角
折射角
(
(
反射光线
光的折射规律
人类经历了一千多年的时间,从积累的入射角i和折射角r的数据中寻求两者之间的定量关系。
6、入射角的正弦和折射角的正弦成正比
=
n12
比例常数
空气→玻璃 n 大于 1
玻璃→空气 n 小于 1
斯涅耳定律
1、规律得出的过程:
2、正确规律的得出往往要经过曲折的过程,要经过实践的多次检验。
自主感悟
古希腊哲学家托勒密的结论:折射角与入射角成正比
荷兰数学家斯涅耳的结论:
折射角与入射角的正弦成正比
托勒密的实验数据记录非常详细、准确,只可惜欠缺数学眼光,致使结论的总结出现错误。而这个看来仅仅一步之遥的距离却又使人类经历了一千五百多年的探索!
7、折射率
(1)折射率-----是光从真空射入某种介质中时的折射率(光从真空射入某种介质时的折射率,叫做该种介质的绝对折射率,也简称为某种介质的折射率.相对折射率在高中不作要求 )
(2)n的大小与介质有关,与θ1和θ2无关,对于确定的介质,n是定值,不能说n∝sinθ1或n∝1/sinθ2
(3)折射率无单位,任何介质的折射率皆大于1。
定义式:
折射率
灵机一动
θ1
θ2
光很有可能是一种波
这跟惠更斯原理揭示的波折射的规律何其相似
光的反射、折射、干涉、衍射、多普勒效应等波动特征在以后的学习中会一一碰到
光确实是一种波
某介质的折射率,等于光在真空中的速度c与光在介质中的速度v之比:
c
v
n=
(n>1)
光在不同介质中的速度不同,这正是发生折射的原因。
研究表明:
折射光路也是可逆的吗?
i
r
空气
水
折射光路是可逆的
[自我检测]
1.正误判断
(1)光从一种介质进入另一种介质时传播方向就会变化。( )
解析 如果光垂直分界面入射时,光的传播方向就不会变化。
答案 ×
(2)介质的密度越大,其折射率一定也越大。( )
解析 介质的折射率与介质的密度没有必然联系,密度大,其折射率不一定大。
答案 ×
(3)光从真空斜射入任何介质时,入射角均大于折射角。( )
答案 √
(4)折射定律是确定折射光线位置的规律。( )
答案 √
(5)光的折射率随入射角增大而增大。( )
答案 ×
例1.(多选)关于光的反射与折射,下列说法正确的是( )
A.光发生反射时,光的传播方向不一定改变
B.光发生反射时,光的传播方向可能偏转90°
C.光发生反射时,光的传播方向一定改变
D.光发生折射时,一定伴随着反射现象
解析 光发生反射时,光的传播方向一定发生改变,且可以改变90°,A项错,B、C两项对;发生折射时,一定伴随着反射现象,但有反射现象,不一定有折射现象,D项对。
答案 BCD
实验:测定玻璃的折射率
三、实验器材
长方形玻璃砖、白纸、木板、大头针、图钉、量角器、三角板(或直尺)、铅笔。
一、实验目的
测定玻璃的折射率。
二、实验原理
用插针法确定光路,找出跟入射光线相对应的出射光线,用量角器测入射角θ1和折射角θ2,根据折射定律计算出玻璃的折射率 。
四、实验步骤
1.用图钉把白纸固定在木板上.
2.在白纸上画一条直线aa′,并取aa′上的一点O为入射点,作过O的法线NN′.
3.画出线段AO作为入射光线,并在AO上插上P1、P2两根大头针.
4.在白纸上放上玻璃砖,使玻璃砖的一条长边与直线aa′对齐,并画出另一条长边的对齐线bb′.
5.眼睛在bb′的一侧透过玻璃砖观察两个大头针并调整视线方向,使P1的像被P2的像挡住,然后在眼睛这一侧插上大头针P3,使P3挡住P1、P2的像,再插上P4,使P4挡住P3和P1、P2的像.
6.移去玻璃砖,拔去大头针,由大头针P3、P4的针孔位置确定出射光线O′B及出射点O′,连接O、O′得线段OO′.
7.用量角器测量入射角θ1和折射角θ2,并查出其正弦值sin θ1和sin θ2.
8.改变入射角,重复实验,算出不同入射角时的,并取平均值.
五、数据处理
1.平均值法
算出不同入射角时的比值 ,最后求出在几次实验中所测的 平均值,即为玻璃砖的折射率。
2.图象法
以sin θ1值为横坐标、以sinθ2值为纵坐标,建立直角坐标系,如图1所示。描数据点,过数据点连线得一条过原点的直线。求解图线斜
率k,则 ,故玻璃砖折射率 。
3.作图法
在找到入射光线和折射光线以后,以入射点O为圆心,以任意长为半径画圆,分别与AO交于C点、OO′(或OO′的延长线)交于D点,过C、D两点分别向NN′作垂线,交NN′于C′、D′,用直尺量出CC′和DD′的长,如图 2所示。由于 , ,且CO=DO,所以折射率 。
六、注意事项
(1)实验时,尽可能将大头针竖直插在纸上,且P1和P2之间,P2与O点之间,P3与P4之间,P3与O′点之间距离要稍大一些。
(2)入射角θ1应适当大一些,以减小测量角度的误差,但入射角不宜太大,也不宜太小。
(3)在操作时,手不能触摸玻璃砖的光洁面。更不能把玻璃砖界面当尺子画界线。
(4)在实验过程中,玻璃砖与白纸的相对位置不能改变。
(5)玻璃砖应选用宽度较大的,宜在5 cm以上。若宽度太小,则测量误差较大。
七、误差分析
(1)入射光线和出射光线确定得不够精确,因此要求插大头针时,两大头针间距应适当大一些。
(2)入射角和折射角的测量造成误差,故入射角应适当大些,以减小测量的相对误差。
1.关于介质的折射率,下列说法正确的是( )
A.由折射率的公式 可知,介质的折射率与入射角θ1的正弦成正比
B.由折射率公式 可知,介质折射率与光在介质中的传播速度v成反比
C.折射率反映的是介质本身的光学性质由介质本身及光的性质共同决定
D.玻璃的折射率大于1,水的折射率小于1
B
2.如图所示是光线以相同的入射角从空气射入三种不同介质时的折射情况,则在三种介质中光的传播速度最小的是( )
A.介质甲 B.介质乙 C.介质丙 D.三种介质均一样
C
3.如图所示,光在真空和某介质界面MN上发生折射,由图可知( )
A.光是从真空射入介质的
B.光是由介质射入真空的
C.介质的折射率为
D.介质的折射率为
B
4.一条光线以40°的入射角从真空中射到平板透明材料上,光的一部分被反射,一部分被折射,折射光线与反射光线的夹角可能( )
A.小于40°
B.在50°~100°之间
C.在100°~140°之间
D.大于140°
C
5.如图所示,用插针法测定玻璃砖折射率的实验中,下列说法中正确的是( )
A.若P1、P2的距离较大时,通过玻璃砖会看不到P1、P2的像
B.为减少测量误差,P1、P2的连线与法线NN'的夹角应尽量小些
C.为了减小作图误差,P3和P4的距离应适当取大些
D.若P1、P2的连线与法线NN'夹角较大时,有可能在bb′面发生全反射
C
6.如图所示,单色光沿AO从空气射入水中,以O点为圆心,作两半径分别为R和r(R>r)的同心圆,大圆与入射光线相交于A,与折射光线相交于B,小圆与AO延长线相交于M,BM连线恰好和水平界面垂直,垂足为N,则下列说法正确的是( )
A.水的折射率
B.光线从空气中进入水中,频率变大了
C.光线在AO段的传播时间tAO的大于在OB段的传播时间tOB
D.由于数据不足,无法确定入射角和折射角的大小,故无法计算折射率
D
7.某同学做测定玻璃折射率实验时,用他测得的多组入射角θ1与折射角θ2作出sinθ1-sinθ2图像,如图所示,则下列判断正确的是( )
A.他做实验时,研究的是光从空气射入玻璃的折射现象
B.玻璃的折射率为0.67
C.玻璃的折射率为1.5
D.他做实验时,研究的是光从玻璃射入空气的折射现象
AC
8.光从某介质射入空气,入射角θ1从零开始增大到某一值的过程中,折射角θ2也随之增大,则下列说法正确的是( )
A.比值 不变
B.比值不变
C.比值 是一个大于1的常数
D.比值 是一个小于1的常数
BD
