8.2.1 消元——解二元一次方程组(代入法)课件(共16张PPT) 2022-2023学年人教版数学七年级下册
文档属性
| 名称 | 8.2.1 消元——解二元一次方程组(代入法)课件(共16张PPT) 2022-2023学年人教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 260.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-06 19:12:23 | ||
图片预览






文档简介
(共16张PPT)
8.2.1代入法
解二元一次方程组
01情境导入
02问题导探
03典例导练
04小结导构
二元一次方程x+y=7
(1)用x的代数式表示y
(2)用y的代数式表示x
x=7-y
y=7-x
y克
.
.
x克
200克
y克
x克
10克
01情境导入
04小结导构
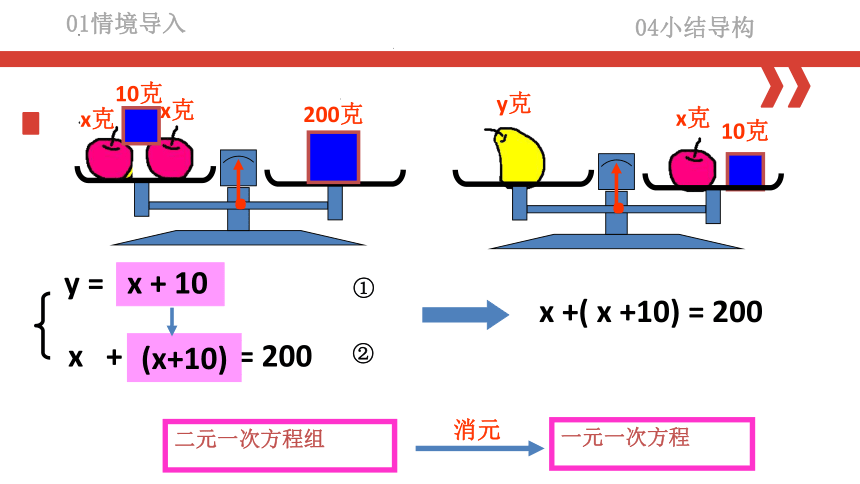
x + y = 200
y = x + 10
一元一次方程
二元一次方程组
消元
x克
10克
(x+10)
x +( x +10) = 200
①
②
03典例导练
01情境导入
02问题导探
04小结导构
例1 解方程组
2y – 3x = 1
x = y - 1
①
②
解:把②代入①得:
2y – 3(y – 1)= 1
解得:y = 2
把y = 2代入②,得
x = 1
∴原方程组的解为
x = 1
y = 2
03典例导练
01情境导入
02问题导探
04小结导构
练1 解方程组
x = 2y
2x + y = 1
(1)
y = 1 – 3x
x - 2y + 9 = 0
(2)
解:把①代入②得:
2 ×2y+y = 1
解得:y =
把y = 代入①,得
x =
∴原方程组的解为
x =
y =
①
②
①
②
解:把①代入②得:
x - 2(1 –3x) + 9 = 0
解得:x = -1
把x = -1代入①,得
y = 4
∴原方程组的解为
x =- 1
y = 4
03典例导练
01情境导入
02问题导探
04小结导构
例2 解方程组
3x – 2y = 19
2x + y = 1
①
②
解:由②得:
y = 1 – 2x
③
把③代入①得:
3x – 2(1 – 2x)= 19
解得:x = 3
把x = 3代入③,得
y
= - 5
∴原方程组的解为
x = 3
y = - 5
1、变形:将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、代入求解(把变形后的方程代入到另一个方程中,消元后求出未知数的值
4、写解
3、回代求解(把求得的未知数的值代入到变形的方程中,求出另一个未知数的值
03典例导练
01情境导入
02问题导探
04小结导构
练2 解方程组
x – 2y = 4
2x + 3y = 1
(1)
x – 2y = 7
3x - 4y = 0
(2)
x = 2
y = -1
x = -14
y = -10.5
03典例导练
01情境导入
02问题导探
04小结导构
x+y =5
2x+3y=11
(3)
3x+2y=13
x-2y=5
(4)
x = 4
y = 1
x = 4.5
y = -0.25
03典例导练
01情境导入
02问题导探
04小结导构
例3 有48支队520名运动员参加篮球、排球比赛,其中每支篮球队10人,每支排 球队12人,每名运动员只能参加一项比赛. 篮球、排球队各有多少支参赛?
解:设篮球队有x支参赛,排球队有y支参赛.
根据题意,得
由①得:y=48-x ③
将③代入②得:10x+12(48-x)=520
03典例导练
01情境导入
02问题导探
04小结导构
解得:x=28
将x=28代入③得:y=20
∴原方程组的解为
答:篮球队有28支参赛,排球队有20支参赛.
03典例导练
01情境导入
02问题导探
04小结导构
练3:张翔从学校出发骑自行车去县城,中途因道路施工步行一段路,1.5 h 后到达县城. 他骑车的平均速度是15 km/h,步行的平均速度是5 km/h,路程全长20 km. 他骑车与步行各用多少时间?
03典例导练
01情境导入
02问题导探
04小结导构
综合运用:
2.如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
1.若方程5x 2m+n + 4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
03典例导练
01情境导入
02问题导探
04小结导构
1、若 则 (b-a)2 015=( )
A.-1 B.1
C.5 2 015 D.-5 2 015
A
当堂练习
03典例导练
01情境导入
02问题导探
04小结导构
3.已知关于x,y的方程组 则y用只含x的式子表示为( )
A.y=2x+7 B.y=7-2x
C.y=-2x-5 D.y=2x-5
B
03典例导练
01情境导入
02问题导探
04小结导构
4.解方程组
x+1=2(y-1)
3(x+1)=5(y-1)
(1)
2x – 7y = 8
3x - 8y = 10
(2)
01情境导入
02问题导探
04小结导构
03典例导练
本节课你收获了什么?
8.2.1代入法
解二元一次方程组
01情境导入
02问题导探
03典例导练
04小结导构
二元一次方程x+y=7
(1)用x的代数式表示y
(2)用y的代数式表示x
x=7-y
y=7-x
y克
.
.
x克
200克
y克
x克
10克
01情境导入
04小结导构
x + y = 200
y = x + 10
一元一次方程
二元一次方程组
消元
x克
10克
(x+10)
x +( x +10) = 200
①
②
03典例导练
01情境导入
02问题导探
04小结导构
例1 解方程组
2y – 3x = 1
x = y - 1
①
②
解:把②代入①得:
2y – 3(y – 1)= 1
解得:y = 2
把y = 2代入②,得
x = 1
∴原方程组的解为
x = 1
y = 2
03典例导练
01情境导入
02问题导探
04小结导构
练1 解方程组
x = 2y
2x + y = 1
(1)
y = 1 – 3x
x - 2y + 9 = 0
(2)
解:把①代入②得:
2 ×2y+y = 1
解得:y =
把y = 代入①,得
x =
∴原方程组的解为
x =
y =
①
②
①
②
解:把①代入②得:
x - 2(1 –3x) + 9 = 0
解得:x = -1
把x = -1代入①,得
y = 4
∴原方程组的解为
x =- 1
y = 4
03典例导练
01情境导入
02问题导探
04小结导构
例2 解方程组
3x – 2y = 19
2x + y = 1
①
②
解:由②得:
y = 1 – 2x
③
把③代入①得:
3x – 2(1 – 2x)= 19
解得:x = 3
把x = 3代入③,得
y
= - 5
∴原方程组的解为
x = 3
y = - 5
1、变形:将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、代入求解(把变形后的方程代入到另一个方程中,消元后求出未知数的值
4、写解
3、回代求解(把求得的未知数的值代入到变形的方程中,求出另一个未知数的值
03典例导练
01情境导入
02问题导探
04小结导构
练2 解方程组
x – 2y = 4
2x + 3y = 1
(1)
x – 2y = 7
3x - 4y = 0
(2)
x = 2
y = -1
x = -14
y = -10.5
03典例导练
01情境导入
02问题导探
04小结导构
x+y =5
2x+3y=11
(3)
3x+2y=13
x-2y=5
(4)
x = 4
y = 1
x = 4.5
y = -0.25
03典例导练
01情境导入
02问题导探
04小结导构
例3 有48支队520名运动员参加篮球、排球比赛,其中每支篮球队10人,每支排 球队12人,每名运动员只能参加一项比赛. 篮球、排球队各有多少支参赛?
解:设篮球队有x支参赛,排球队有y支参赛.
根据题意,得
由①得:y=48-x ③
将③代入②得:10x+12(48-x)=520
03典例导练
01情境导入
02问题导探
04小结导构
解得:x=28
将x=28代入③得:y=20
∴原方程组的解为
答:篮球队有28支参赛,排球队有20支参赛.
03典例导练
01情境导入
02问题导探
04小结导构
练3:张翔从学校出发骑自行车去县城,中途因道路施工步行一段路,1.5 h 后到达县城. 他骑车的平均速度是15 km/h,步行的平均速度是5 km/h,路程全长20 km. 他骑车与步行各用多少时间?
03典例导练
01情境导入
02问题导探
04小结导构
综合运用:
2.如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
1.若方程5x 2m+n + 4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
03典例导练
01情境导入
02问题导探
04小结导构
1、若 则 (b-a)2 015=( )
A.-1 B.1
C.5 2 015 D.-5 2 015
A
当堂练习
03典例导练
01情境导入
02问题导探
04小结导构
3.已知关于x,y的方程组 则y用只含x的式子表示为( )
A.y=2x+7 B.y=7-2x
C.y=-2x-5 D.y=2x-5
B
03典例导练
01情境导入
02问题导探
04小结导构
4.解方程组
x+1=2(y-1)
3(x+1)=5(y-1)
(1)
2x – 7y = 8
3x - 8y = 10
(2)
01情境导入
02问题导探
04小结导构
03典例导练
本节课你收获了什么?
