15.4电阻的串联和并联 课件(共20张PPT)2023-2024学年沪科版物理九年级全一册
文档属性
| 名称 | 15.4电阻的串联和并联 课件(共20张PPT)2023-2024学年沪科版物理九年级全一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 607.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-06 11:43:27 | ||
图片预览



文档简介
(共20张PPT)
15.4 电阻的串联和并联
学习目标
1.知道串联电路和并联电路中电阻间的关系。
2.能用欧姆定律结合串、并联电路中电流、电压、电阻的关系进行综合计算。
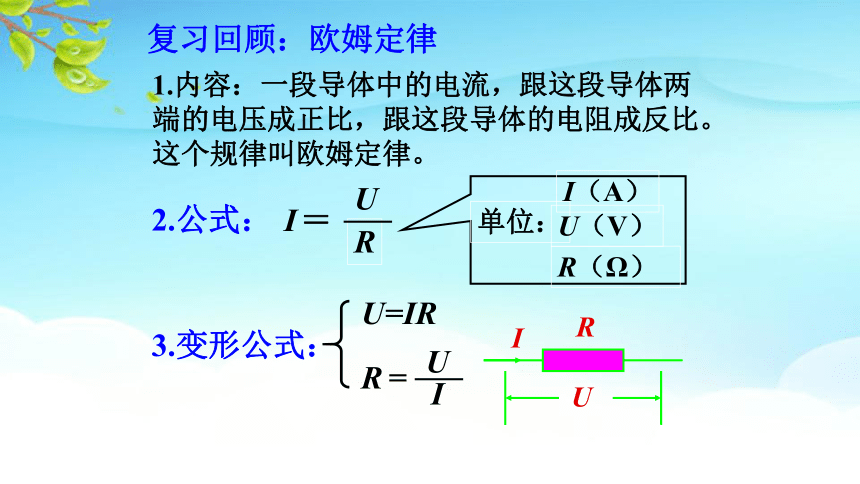
复习回顾:欧姆定律
1.内容:一段导体中的电流,跟这段导体两端的电压成正比,跟这段导体的电阻成反比。这个规律叫欧姆定律。
2.公式:
I
R
U
=
3.变形公式:
U=IR
R
=
I
U
R(Ω)
单位:
I(A)
U(V)
R
U
I
V1
V2
A2
A1
V
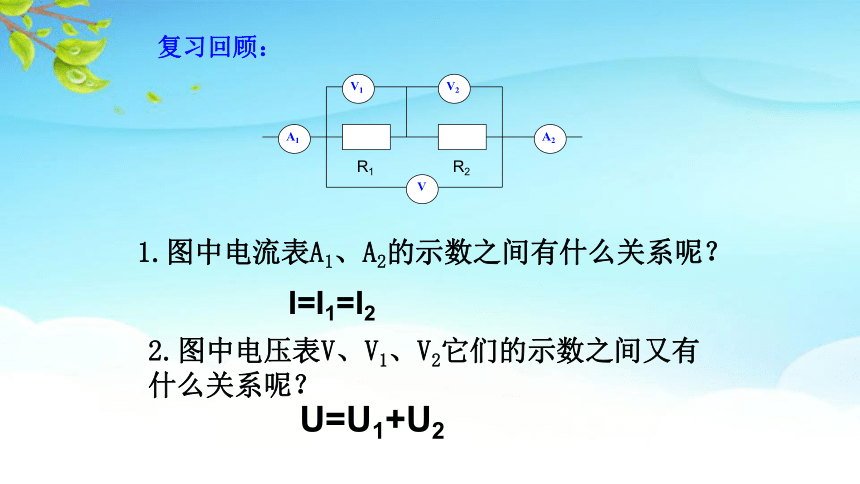
1.图中电流表A1、A2的示数之间有什么关系呢?
2.图中电压表V、V1、V2它们的示数之间又有什么关系呢?
复习回顾:
R1
R2
U=U1+U2
I=I1=I2
A1
V2
V1
A
A2
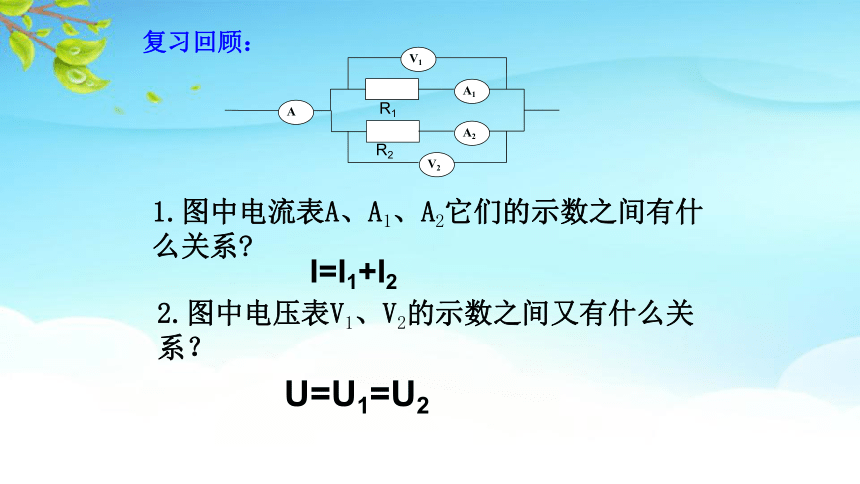
1.图中电流表A、A1、A2它们的示数之间有什么关系
2.图中电压表V1、V2的示数之间又有什么关系?
复习回顾:
R1
R2
I=I1+I2
U=U1=U2
我们已经掌握了:
串联电路
串联电路中各处电流相等。
串联电路两端的总电压等于各部分两端的电压之和。
并联电路
并联电路中各支路两端的电压相等。
并联电路干路的总电流等于各支路的电流之和。
我们又有了新的问题:电阻串联或并联时,总电阻与参与串联或并联的电阻是什么关系呢?是比原来大了还是小了?
I=I1=I2
I=I1+I2
U=U1+U2
U=U1=U2
串联电路中的电阻有什么规律?
我们可以应用实验和欧姆定律进行研究。
串联电路的总电阻特点
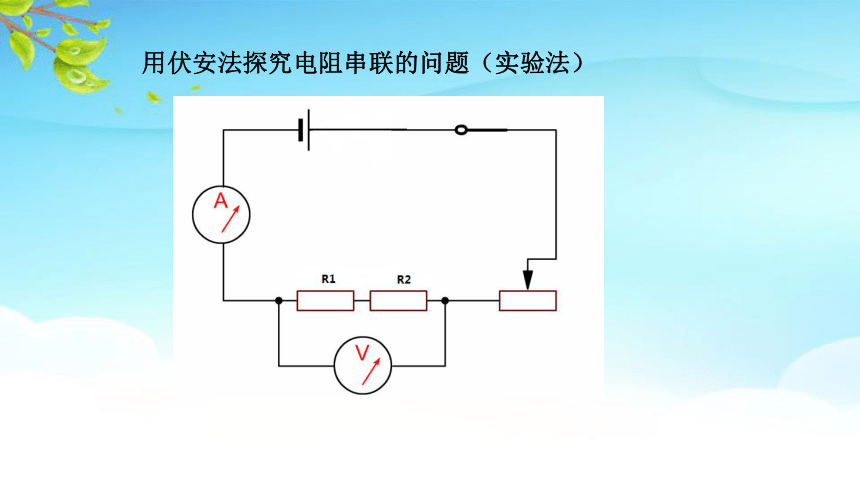
用伏安法探究电阻串联的问题(实验法)
推导法:
R1
R2
U1
U2
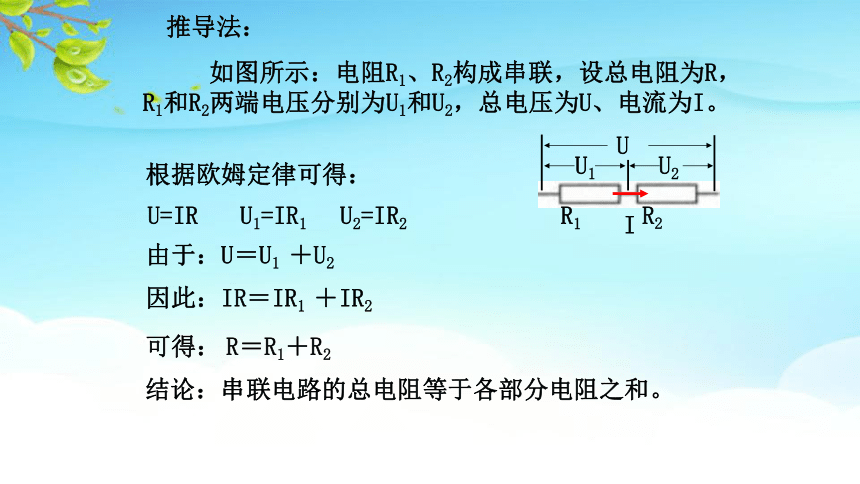
如图所示:电阻R1、R2构成串联,设总电阻为R,R1和R2两端电压分别为U1和U2,总电压为U、电流为I。
由于:U=U1 +U2
根据欧姆定律可得:
可得:
因此:IR=IR1 +IR2
R=R1+R2
U
结论:串联电路的总电阻等于各部分电阻之和。
I
U=IR U1=IR1 U2=IR2
1、串联电路的总电阻特点(记录)
串联电路总电阻大于其中任何一个导体的电阻值。
+
=
因为导体串联相当于增加了导体的长度
2、 若有n 个电阻R1、R2、···、Rn串 联,则它们的总电阻R 等于多少?
R=R1+R2+···+Rn
3、n个相同阻值电阻RO串联,总电阻R=nR
并联电路总电阻小于各支路电阻,
因为电阻并联相当于增大导体的横截面积。
1、并联电路的总电阻特点
2、n个相同阻值R0电阻并联,总电阻
R= R0
串联电路 并联电路
电流的特点
电压的特点
电阻的特点
电流电压电阻之间关系
I = I1 = I2
R=R1+R2
U=U1+U2
I一定,电压与电阻成正比
I = I1 + I2
U=U1=U2
1/R=1/R1+1/R2
U一定,电流与电阻成反比
小结
提出问题:
几个电阻并联后的总电阻,与各个分电阻相比,是大了还是小了?
猜想与假设:
两段导体并在一起,相当于导体的横截面积变 ,因此,其电阻值可能会 。
大
变小
二、并联电阻的规律
进行实验与收集证据
—
0.6
3
A
B
R
R
10Ω
15Ω
6Ω
1、电阻并联后总电阻的阻值比任何一个分电阻的阻值
得出结论
都小
例:一个阻为1Ω的电阻与一个阻值为1000Ω的电阻并联,其总电阻为( )A.大于1000Ω B.小于1Ω
C.大于1Ω且小于1000Ω
D.无法确定
B
让我们一起来推导公式:
等效于
R
U
I
I
I1
I2
U
由欧姆定律,可得:
由于I=I1+I2,所以:
2、两个并联:总电阻的倒数等于两分电阻的倒数之和。
即
问题1、n个阻值不同的电阻并联,总电阻与各个电阻的关系
(2).n个阻值相同的电阻Ro并联,总电阻与各个电阻的关系:
⑴.电阻R1R2并联,总电阻:
例两个10Ω的电阻并联,则总电阻为__Ω,如果是10个并联,则总电阻为___Ω。
例一个20Ω的电阻与一个30Ω的电阻并联,则总电阻为___Ω。
5
1
12
∴ R=12Ω
串、并联电路电流、电压、电阻的规律总结:
串联电路 并联电路
电流 I=I1=I2 I=I1+I2
电压 U=U1+U2 U=U1=U2
电阻 R总=R1+R2
分压或 分流
课堂小结
谢 谢!
15.4 电阻的串联和并联
学习目标
1.知道串联电路和并联电路中电阻间的关系。
2.能用欧姆定律结合串、并联电路中电流、电压、电阻的关系进行综合计算。
复习回顾:欧姆定律
1.内容:一段导体中的电流,跟这段导体两端的电压成正比,跟这段导体的电阻成反比。这个规律叫欧姆定律。
2.公式:
I
R
U
=
3.变形公式:
U=IR
R
=
I
U
R(Ω)
单位:
I(A)
U(V)
R
U
I
V1
V2
A2
A1
V
1.图中电流表A1、A2的示数之间有什么关系呢?
2.图中电压表V、V1、V2它们的示数之间又有什么关系呢?
复习回顾:
R1
R2
U=U1+U2
I=I1=I2
A1
V2
V1
A
A2
1.图中电流表A、A1、A2它们的示数之间有什么关系
2.图中电压表V1、V2的示数之间又有什么关系?
复习回顾:
R1
R2
I=I1+I2
U=U1=U2
我们已经掌握了:
串联电路
串联电路中各处电流相等。
串联电路两端的总电压等于各部分两端的电压之和。
并联电路
并联电路中各支路两端的电压相等。
并联电路干路的总电流等于各支路的电流之和。
我们又有了新的问题:电阻串联或并联时,总电阻与参与串联或并联的电阻是什么关系呢?是比原来大了还是小了?
I=I1=I2
I=I1+I2
U=U1+U2
U=U1=U2
串联电路中的电阻有什么规律?
我们可以应用实验和欧姆定律进行研究。
串联电路的总电阻特点
用伏安法探究电阻串联的问题(实验法)
推导法:
R1
R2
U1
U2
如图所示:电阻R1、R2构成串联,设总电阻为R,R1和R2两端电压分别为U1和U2,总电压为U、电流为I。
由于:U=U1 +U2
根据欧姆定律可得:
可得:
因此:IR=IR1 +IR2
R=R1+R2
U
结论:串联电路的总电阻等于各部分电阻之和。
I
U=IR U1=IR1 U2=IR2
1、串联电路的总电阻特点(记录)
串联电路总电阻大于其中任何一个导体的电阻值。
+
=
因为导体串联相当于增加了导体的长度
2、 若有n 个电阻R1、R2、···、Rn串 联,则它们的总电阻R 等于多少?
R=R1+R2+···+Rn
3、n个相同阻值电阻RO串联,总电阻R=nR
并联电路总电阻小于各支路电阻,
因为电阻并联相当于增大导体的横截面积。
1、并联电路的总电阻特点
2、n个相同阻值R0电阻并联,总电阻
R= R0
串联电路 并联电路
电流的特点
电压的特点
电阻的特点
电流电压电阻之间关系
I = I1 = I2
R=R1+R2
U=U1+U2
I一定,电压与电阻成正比
I = I1 + I2
U=U1=U2
1/R=1/R1+1/R2
U一定,电流与电阻成反比
小结
提出问题:
几个电阻并联后的总电阻,与各个分电阻相比,是大了还是小了?
猜想与假设:
两段导体并在一起,相当于导体的横截面积变 ,因此,其电阻值可能会 。
大
变小
二、并联电阻的规律
进行实验与收集证据
—
0.6
3
A
B
R
R
10Ω
15Ω
6Ω
1、电阻并联后总电阻的阻值比任何一个分电阻的阻值
得出结论
都小
例:一个阻为1Ω的电阻与一个阻值为1000Ω的电阻并联,其总电阻为( )A.大于1000Ω B.小于1Ω
C.大于1Ω且小于1000Ω
D.无法确定
B
让我们一起来推导公式:
等效于
R
U
I
I
I1
I2
U
由欧姆定律,可得:
由于I=I1+I2,所以:
2、两个并联:总电阻的倒数等于两分电阻的倒数之和。
即
问题1、n个阻值不同的电阻并联,总电阻与各个电阻的关系
(2).n个阻值相同的电阻Ro并联,总电阻与各个电阻的关系:
⑴.电阻R1R2并联,总电阻:
例两个10Ω的电阻并联,则总电阻为__Ω,如果是10个并联,则总电阻为___Ω。
例一个20Ω的电阻与一个30Ω的电阻并联,则总电阻为___Ω。
5
1
12
∴ R=12Ω
串、并联电路电流、电压、电阻的规律总结:
串联电路 并联电路
电流 I=I1=I2 I=I1+I2
电压 U=U1+U2 U=U1=U2
电阻 R总=R1+R2
分压或 分流
课堂小结
谢 谢!
同课章节目录
- 第十二章 温度与物态变化
- 第一节 温度与温度计
- 第二节 熔化与凝固
- 第三节 汽化与液化
- 第四节 升华与凝华
- 第五节 全球变暖与水资源危机
- 第十三章 内能与热机
- 第一节 物体的内能
- 第二节 科学探究:物质的比热容
- 第三节 内燃机
- 第四节 热机效率和环境保护
- 第十四章 了解电路
- 第一节 电是什么
- 第二节 让电灯发光
- 第三节 连接串联电路和并联电路
- 第四节 科学探究:串联和并联电路的电流
- 第五节 测量电压
- 第十五章 探究电路
- 第一节 电阻和变阻器
- 第二节 科学探究:欧姆定律
- 第三节 “伏安法”测电阻
- 第四节 电阻的串联和并联
- 第五节 家庭用电
- 第十六章 电流做功与电功率
- 第一节 电流做功
- 第二节 电流做功的快慢
- 第三节 测量电功率
- 第四节 科学探究:电流的热效应
- 第十七章 从指南针到磁浮列车
- 第一节 磁是什么
- 第二节 电流的磁场
- 第三节 科学探究:电动机为什么会转动
- 第十八章 电能从哪里来
- 第一节 电能的产生
- 第二节 科学探究:怎样产生感应电流
- 第三节 电能的输送
- 第十九章 走进信息时代
- 第一节 感受信息
- 第二节 让信息“飞”起来
- 第三节 踏上信息高速公路
- 第二十章 能源、材料与社会
- 第一节 能量的转化与守恒
- 第二节 能源的开发和利用
- 第三节 材料的开发和利用
