3.4.2力的合成与分解课件(共42张PPT)高一上学期物理人教版(2019)必修第一册
文档属性
| 名称 | 3.4.2力的合成与分解课件(共42张PPT)高一上学期物理人教版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 37.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-06 19:15:08 | ||
图片预览





文档简介
(共42张PPT)
3.4 力的合成与分解
新课引入
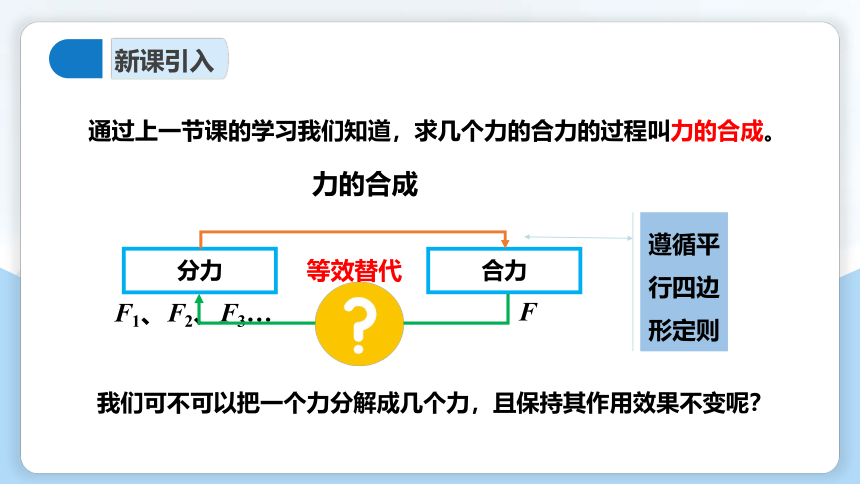
通过上一节课的学习我们知道,求几个力的合力的过程叫力的合成。
分力
合力
等效替代
F
F1、F2、F3…
力的合成
我们可不可以把一个力分解成几个力,且保持其作用效果不变呢?
遵循平行四边形定则
力的分解
力的分解
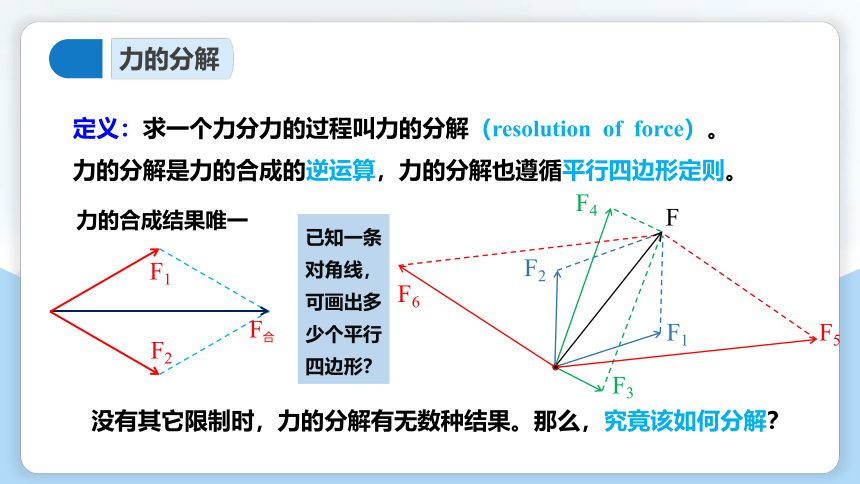
定义:求一个力分力的过程叫力的分解(resolution of force)。
力的分解是力的合成的逆运算,力的分解也遵循平行四边形定则。
F合
力的合成结果唯一
F1
F2
F3
F4
F5
F6
F
F1
F2
没有其它限制时,力的分解有无数种结果。那么,究竟该如何分解?
已知一条对角线,可画出多少个平行四边形?
亲自体会
动手试试:如图,用铅笔支起图中的绳子
F的作用效果:
①橡皮条被拉伸
②掌心受到压力
A
B
C
θ
F
F1
θ
F2
看来按力的作用效果来分解比较合适
分解方式探究
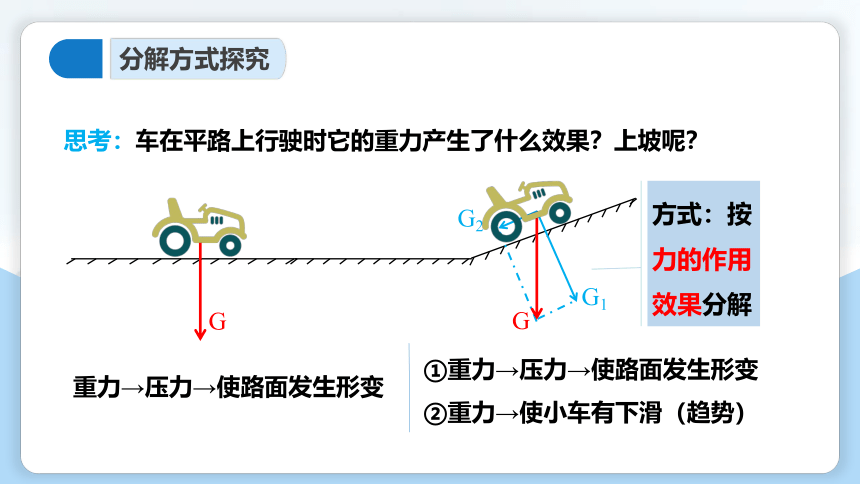
思考:车在平路上行驶时它的重力产生了什么效果?上坡呢?
G
重力→压力→使路面发生形变
G
G1
G2
①重力→压力→使路面发生形变
②重力→使小车有下滑(趋势)
方式:按力的作用效果分解
力的分解步骤
力的分解步骤:
1.分析力的作用效果;
2.据力的作用效果定分力的方向;(画两个分力的方向)
3.用平行四边形定则定分力的大小;
4.据数学知识求分力的大小和方向。
可以举例说明吗?
实例分析
问题模型1
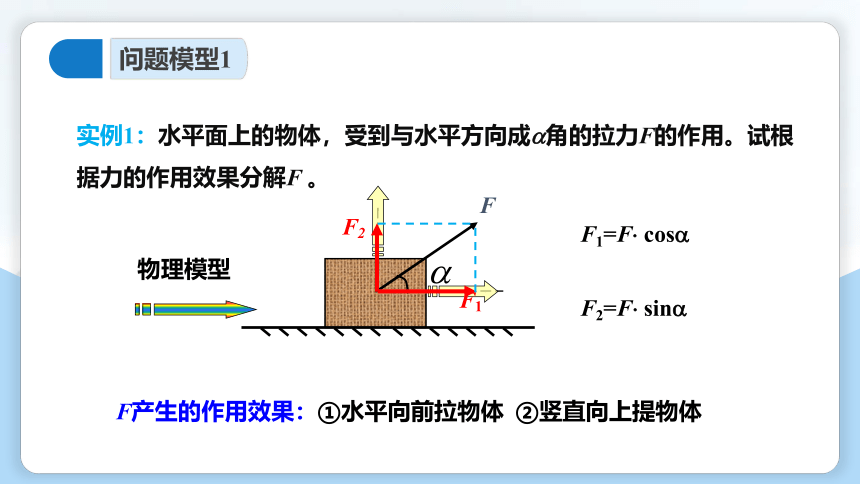
实例1:水平面上的物体,受到与水平方向成 角的拉力F的作用。试根据力的作用效果分解F 。
物理模型
F
F1=F cos
F2=F sin
F1
F2
F产生的作用效果:①水平向前拉物体 ②竖直向上提物体
问题模型2
物理模型
按照力的作用效果分解
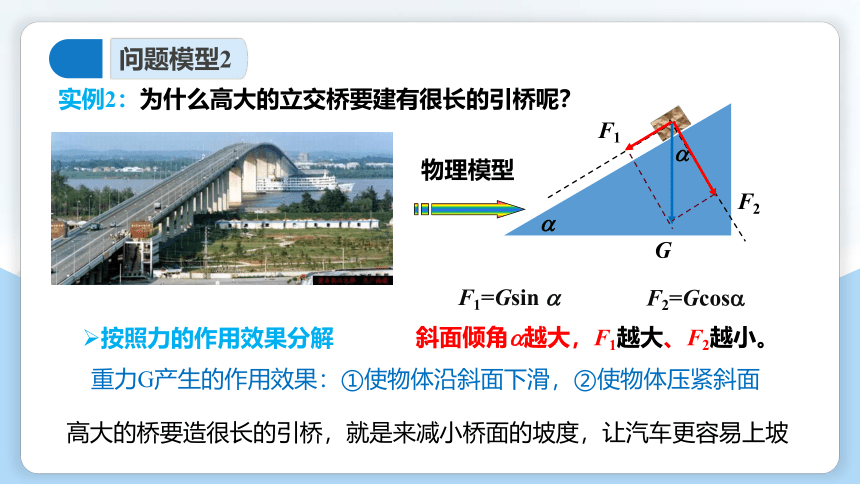
实例2:为什么高大的立交桥要建有很长的引桥呢?
G
F1
F2
F1=Gsin
F2=Gcos
斜面倾角 越大,F1越大、F2越小。
重力G产生的作用效果:①使物体沿斜面下滑,②使物体压紧斜面
高大的桥要造很长的引桥,就是来减小桥面的坡度,让汽车更容易上坡
问题模型3
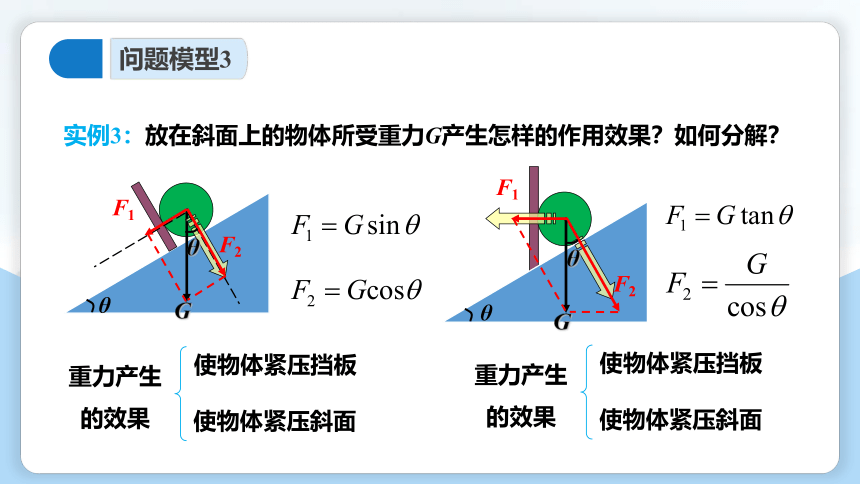
实例3:放在斜面上的物体所受重力G产生怎样的作用效果?如何分解?
θ
G
F1
F2
θ
θ
F1
F2
G
θ
重力产生的效果
使物体紧压挡板
使物体紧压斜面
重力产生的效果
使物体紧压挡板
使物体紧压斜面
问题模型4
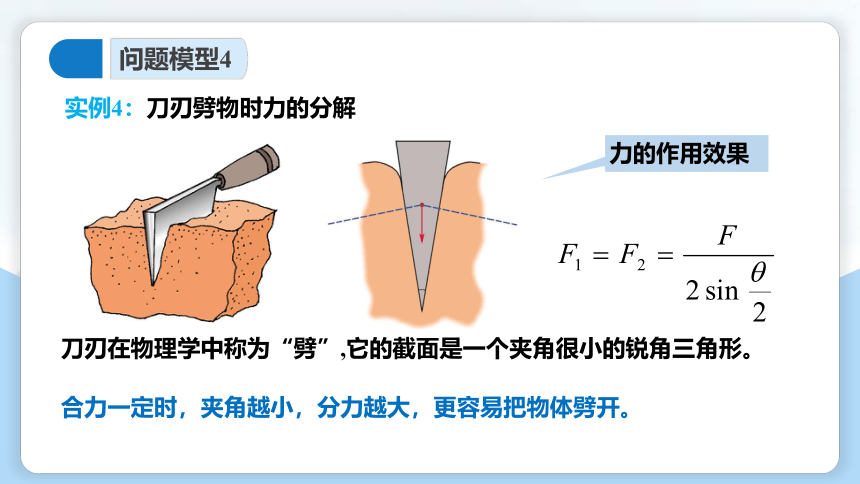
刀刃在物理学中称为“劈”,它的截面是一个夹角很小的锐角三角形。
实例4:刀刃劈物时力的分解
力的作用效果
合力一定时,夹角越小,分力越大,更容易把物体劈开。
问题模型4
学生活动:找一找衣服上的“劈”
F
F1
F2
F
F1
F2
F
F1
F2
规律总结
力的分解时一般按力的作用效果和实际需要进行分解
某同学用轻质圆规做了如图所示的小实验,圆规两脚A与B分别模拟横梁与斜梁,钥匙模拟重力,重力为mg,将钥匙对绳子的拉力分解为拉伸A脚的分力F1和压缩B脚的分力F2,则
A.F1=mgtan α B.F1=mgsin α
C.F2=mgtan α D.F2=mgsin α
例1
√
在日常生活中,力的分解有着广泛的应用,如图甲用斧子把木桩劈开,已知两个侧面之间的夹角为2θ,斧子对木桩施加一个向下的力F时,产生了大小相等的两个侧向分力F1、F2,由图乙可得下列关系正确的是
例2
√
力的正交
分解
力的正交分解
力的正交分解:将力沿两互相垂的方向分解
Fx
Fy
Fy=F·sinθ
x方向的分力:
Fx =F·cosθ
0
x
y
y方向的分力:
θ
F
为什么要正交分解呢?
正交分解的目的和思想
化复杂的矢量运算为普通的代数运算,将力的合成化简为同向或反向或垂直方向。便于运用普通代数运算公式来解决矢量的运算。
1.正交分解的目的
正交分解法求合力,运用了“欲合先分”的策略,即为了合成而分解,降低了运算的难度,是一种重要思想方法。
2.正交分解的基本思想
分解时最好兼顾力的实际效果
正交分解的步骤
F1
F2
x
y
O
F2y
F1y
F1x
F2X
2.将不在坐标轴上的力分解到坐标轴上;
1.建立xoy直角坐标系
F1X=F1cosθ1
F1y=F1sinθ1
F2X=F2cosθ2
F2y=F2sinθ2
F1
F2
θ1
θ2
3.分别求出x轴、y轴上各分力的矢量和,即
Fx=F1x+F2x+……
Fy=F1y+F2y+……
4.求共点力的合力:
与x轴正方向的夹角为θ
x
y
o
FX
Fy
F
θ
大小:
方向:
正交分解的步骤
正交分解的两种常见模型
F拉
θ
x
y
G
f静
N
o
F2
F1
θ
O
x
y
v
G
F
N
f滑
典例分析
如图所示,静置于水平面上的长方体木箱,受到与水平面成的拉力F的作用,现将该拉力分解为水平分力和竖直分力,则以下关系正确的是( )
A. B. C. D.
如图所示,一个物体在平面直角坐标系的坐标原点,只受到F1和F2的作用F1 =10N, ,则物体的合力( )
A.方向沿+x B.方向沿-x
C.大小等于10N D.大小等于
典例分析
一个物体受到四个力的作用,已知F1=1N,方向正东;F2=2N,方向东偏北600,F3=N,方向西偏北300;F4=4N,方向东偏南600,求物体所受的合力。
【解析】
F1
F2
F3
F4
x
y
F2x
F2y
F3y
F3x
F4x
F4y
600
300
600
Fy= N
Fx = -1/2 N
F =1N
x
y
【解析】
典例分析
在同一平面内的三个力F1、F2、F3的大小依次为18 N、40 N、24 N,方向如图所示,求它们的合力。(sin 37°=0.6,cos 37°=0.8)
例3
50 N,方向与F1相同
如图所示,倾角为15°的斜面上放着木箱,用100 N的拉力斜向上拉着木箱,F与水平方向成45°角。分别以平行于斜面和垂直于斜面的方向为x轴和y轴建立直角坐标系,把F分解为沿着两个坐标轴的分力。试在图中作出分力Fx和Fy,并计算它们的大小。
例4
力的分解
分类讨论
几种常见情况
当一个确定的力加上相应条件限制,它的分解情况是否是唯一的?
1.已知两分力的方向:
2.已知一个分力的大小和方向:
F
F
F1
F1
F2
F2
唯一解
唯一解
几种常见情况
3.已知一个确定的合力和两个分力F1和F2的大小:
两个解
F1+F2>F
F1+F2=F
F1+F2<F
F2
F1
F
F2
F1
F
F
F1
F2
F2
F1
F
无解
一个解
F1、F2和F一起构成封闭三角形
4.已知一个确定的合力和一个分力F1的方向和另一个分力F2的大小:
O
F
F1
θ
①当 F2< Fsinθ 时,无解;
②当 F2=Fsinθ 时,有唯一解;
③当 Fsinθ④当 F2≥F 时, 有唯一解。
几种常见情况
已知两个共点力的合力为50 N,分力F1的方向与合力F的方向成30°角,分力F2的大小为30 N,则
A.F1的大小是唯一的 B.F2的方向是唯一的
C.F2有两个方向 D.F2可取任意方向
例5
√
(多选)如图所示,将一个已知力F分解为F1和F2,已知F=10 N,F1与F的夹角为37°(已知sin 37°=0.6,cos 37°=0.8),则F2的大小
A.可能大于10 N B.不可能等于10 N
C.可能小于10 N D.最小值为8 N
例6
√
√
矢量与标量
矢量与标量
标量:在物理学中,只有大小而没有方向的物理量叫标量。
矢量:在物理学中,既有大小又有方向的物理量叫矢量。
如:力、位移、速度、加速度等
如:时间、路程、质量、温度、长度、能量、速率等
矢量运算遵循平行四边形定则
标量运算遵循算术加法法则
巩固提升
第四部分
课堂小结
力的
分解
01
02
实例分析
04
正交
分解
03
分类
讨论
力的分解是力的合成的逆运算,力的分解也遵循平行四边形定则。
已知一个确定的合力和一个分力F1的方向和另一个分力F2的大小:
①当 F2< Fsinθ 时,无解;
②当 F2=Fsinθ 时,有唯一解;
③当 Fsinθ④当 F2≥F 时, 有唯一解。
力的正交分解:将力沿两互相垂的方向分解
力的分解的方法:按实际作用效果分解力。
练习1
如图所示,某工人正在修理草坪,推力F与水平方向成α角,则推力在水平方向的分力为( )
A.Fsinα B.Fcosα
C. D.
精选练习
【参考答案:B】
练习2
车载手机支架是一种非常实用的小工具,可将其简化成相互垂直的斜面AB和斜面BC(如图),斜面BC与水平面的夹角为θ,质量为m的手机在两个斜面之间保持静止,重力加速度为g。将重力沿AB、BC方向分解,则沿斜面AB的分力大小为( )
A.mgsinθ B.mgcosθ
C. D.
精选练习
【参考答案:B】
练习3
明朝谢肇淛的《五杂组》中记载:“明姑苏虎丘寺庙倾侧,议欲正之,非万缗不可。一游僧见之,曰:无烦也,我能正之、”游僧每天将木楔从塔身倾斜一侧的砖缝间敲进去,经月余扶正了塔身。假设所用的木楔为等腰三角形,木楔的顶角为θ,现在木楔背上加一力F,方向如图所示,木楔两侧产生推力FN,则( )
A.若F一定,θ大时FN大 B.若F一定,θ小时FN大
C.若θ一定,F大时FN小 D.若θ一定,F小时FN大
精选练习
【参考答案:B】
练习4
如图所示,将力F分解为F1和F2两个分力,若已知F1的大小,F2与F之间的夹角α,且α为锐角。在求解F2大小时( )
A.若F1>Fsinα时,则F2一定有两解
B.若F1=Fsinα时,则F2有唯一解
C.若F1D.若F1>F时,则F2一定无解
精选练习
【参考答案:B】
练习5
如图所示,质量为的物体放在水平面上,物体与水平面间的动摩擦因数,g取。当物体做匀速直线运动时,下列说法正确的是( )
A.牵引力F的最小值为
B.牵引力F的最小值为
C.最小牵引力F与水平面的夹角为
D.最小牵引力F与水平面的夹角为
精选练习
【参考答案:D】
解析
分析物体受力情况,受到重力、支持力、拉力、摩擦力,建立直角坐标系进行力的分解,如图所示,根据平衡条件得根据摩擦力的计算公式可得
联立解得
其中则所以F的最小值为
此时,故选D。
精选练习
【参考答案:D】
练习6
同在xOy平面内的六个力如图所示,大小分别为F1=10N,,F3=12N,,F5=30N,F6=12N,求合力的大小和方向。
精选练习
解析
根据平行四边形定则将各力垂直分解到两个坐标轴上,则可得x轴方向的合力为
y轴方向的合力为
所以合力大小为
方向沿x正方向。
精选练习
3.4 力的合成与分解
新课引入
通过上一节课的学习我们知道,求几个力的合力的过程叫力的合成。
分力
合力
等效替代
F
F1、F2、F3…
力的合成
我们可不可以把一个力分解成几个力,且保持其作用效果不变呢?
遵循平行四边形定则
力的分解
力的分解
定义:求一个力分力的过程叫力的分解(resolution of force)。
力的分解是力的合成的逆运算,力的分解也遵循平行四边形定则。
F合
力的合成结果唯一
F1
F2
F3
F4
F5
F6
F
F1
F2
没有其它限制时,力的分解有无数种结果。那么,究竟该如何分解?
已知一条对角线,可画出多少个平行四边形?
亲自体会
动手试试:如图,用铅笔支起图中的绳子
F的作用效果:
①橡皮条被拉伸
②掌心受到压力
A
B
C
θ
F
F1
θ
F2
看来按力的作用效果来分解比较合适
分解方式探究
思考:车在平路上行驶时它的重力产生了什么效果?上坡呢?
G
重力→压力→使路面发生形变
G
G1
G2
①重力→压力→使路面发生形变
②重力→使小车有下滑(趋势)
方式:按力的作用效果分解
力的分解步骤
力的分解步骤:
1.分析力的作用效果;
2.据力的作用效果定分力的方向;(画两个分力的方向)
3.用平行四边形定则定分力的大小;
4.据数学知识求分力的大小和方向。
可以举例说明吗?
实例分析
问题模型1
实例1:水平面上的物体,受到与水平方向成 角的拉力F的作用。试根据力的作用效果分解F 。
物理模型
F
F1=F cos
F2=F sin
F1
F2
F产生的作用效果:①水平向前拉物体 ②竖直向上提物体
问题模型2
物理模型
按照力的作用效果分解
实例2:为什么高大的立交桥要建有很长的引桥呢?
G
F1
F2
F1=Gsin
F2=Gcos
斜面倾角 越大,F1越大、F2越小。
重力G产生的作用效果:①使物体沿斜面下滑,②使物体压紧斜面
高大的桥要造很长的引桥,就是来减小桥面的坡度,让汽车更容易上坡
问题模型3
实例3:放在斜面上的物体所受重力G产生怎样的作用效果?如何分解?
θ
G
F1
F2
θ
θ
F1
F2
G
θ
重力产生的效果
使物体紧压挡板
使物体紧压斜面
重力产生的效果
使物体紧压挡板
使物体紧压斜面
问题模型4
刀刃在物理学中称为“劈”,它的截面是一个夹角很小的锐角三角形。
实例4:刀刃劈物时力的分解
力的作用效果
合力一定时,夹角越小,分力越大,更容易把物体劈开。
问题模型4
学生活动:找一找衣服上的“劈”
F
F1
F2
F
F1
F2
F
F1
F2
规律总结
力的分解时一般按力的作用效果和实际需要进行分解
某同学用轻质圆规做了如图所示的小实验,圆规两脚A与B分别模拟横梁与斜梁,钥匙模拟重力,重力为mg,将钥匙对绳子的拉力分解为拉伸A脚的分力F1和压缩B脚的分力F2,则
A.F1=mgtan α B.F1=mgsin α
C.F2=mgtan α D.F2=mgsin α
例1
√
在日常生活中,力的分解有着广泛的应用,如图甲用斧子把木桩劈开,已知两个侧面之间的夹角为2θ,斧子对木桩施加一个向下的力F时,产生了大小相等的两个侧向分力F1、F2,由图乙可得下列关系正确的是
例2
√
力的正交
分解
力的正交分解
力的正交分解:将力沿两互相垂的方向分解
Fx
Fy
Fy=F·sinθ
x方向的分力:
Fx =F·cosθ
0
x
y
y方向的分力:
θ
F
为什么要正交分解呢?
正交分解的目的和思想
化复杂的矢量运算为普通的代数运算,将力的合成化简为同向或反向或垂直方向。便于运用普通代数运算公式来解决矢量的运算。
1.正交分解的目的
正交分解法求合力,运用了“欲合先分”的策略,即为了合成而分解,降低了运算的难度,是一种重要思想方法。
2.正交分解的基本思想
分解时最好兼顾力的实际效果
正交分解的步骤
F1
F2
x
y
O
F2y
F1y
F1x
F2X
2.将不在坐标轴上的力分解到坐标轴上;
1.建立xoy直角坐标系
F1X=F1cosθ1
F1y=F1sinθ1
F2X=F2cosθ2
F2y=F2sinθ2
F1
F2
θ1
θ2
3.分别求出x轴、y轴上各分力的矢量和,即
Fx=F1x+F2x+……
Fy=F1y+F2y+……
4.求共点力的合力:
与x轴正方向的夹角为θ
x
y
o
FX
Fy
F
θ
大小:
方向:
正交分解的步骤
正交分解的两种常见模型
F拉
θ
x
y
G
f静
N
o
F2
F1
θ
O
x
y
v
G
F
N
f滑
典例分析
如图所示,静置于水平面上的长方体木箱,受到与水平面成的拉力F的作用,现将该拉力分解为水平分力和竖直分力,则以下关系正确的是( )
A. B. C. D.
如图所示,一个物体在平面直角坐标系的坐标原点,只受到F1和F2的作用F1 =10N, ,则物体的合力( )
A.方向沿+x B.方向沿-x
C.大小等于10N D.大小等于
典例分析
一个物体受到四个力的作用,已知F1=1N,方向正东;F2=2N,方向东偏北600,F3=N,方向西偏北300;F4=4N,方向东偏南600,求物体所受的合力。
【解析】
F1
F2
F3
F4
x
y
F2x
F2y
F3y
F3x
F4x
F4y
600
300
600
Fy= N
Fx = -1/2 N
F =1N
x
y
【解析】
典例分析
在同一平面内的三个力F1、F2、F3的大小依次为18 N、40 N、24 N,方向如图所示,求它们的合力。(sin 37°=0.6,cos 37°=0.8)
例3
50 N,方向与F1相同
如图所示,倾角为15°的斜面上放着木箱,用100 N的拉力斜向上拉着木箱,F与水平方向成45°角。分别以平行于斜面和垂直于斜面的方向为x轴和y轴建立直角坐标系,把F分解为沿着两个坐标轴的分力。试在图中作出分力Fx和Fy,并计算它们的大小。
例4
力的分解
分类讨论
几种常见情况
当一个确定的力加上相应条件限制,它的分解情况是否是唯一的?
1.已知两分力的方向:
2.已知一个分力的大小和方向:
F
F
F1
F1
F2
F2
唯一解
唯一解
几种常见情况
3.已知一个确定的合力和两个分力F1和F2的大小:
两个解
F1+F2>F
F1+F2=F
F1+F2<F
F2
F1
F
F2
F1
F
F
F1
F2
F2
F1
F
无解
一个解
F1、F2和F一起构成封闭三角形
4.已知一个确定的合力和一个分力F1的方向和另一个分力F2的大小:
O
F
F1
θ
①当 F2< Fsinθ 时,无解;
②当 F2=Fsinθ 时,有唯一解;
③当 Fsinθ
几种常见情况
已知两个共点力的合力为50 N,分力F1的方向与合力F的方向成30°角,分力F2的大小为30 N,则
A.F1的大小是唯一的 B.F2的方向是唯一的
C.F2有两个方向 D.F2可取任意方向
例5
√
(多选)如图所示,将一个已知力F分解为F1和F2,已知F=10 N,F1与F的夹角为37°(已知sin 37°=0.6,cos 37°=0.8),则F2的大小
A.可能大于10 N B.不可能等于10 N
C.可能小于10 N D.最小值为8 N
例6
√
√
矢量与标量
矢量与标量
标量:在物理学中,只有大小而没有方向的物理量叫标量。
矢量:在物理学中,既有大小又有方向的物理量叫矢量。
如:力、位移、速度、加速度等
如:时间、路程、质量、温度、长度、能量、速率等
矢量运算遵循平行四边形定则
标量运算遵循算术加法法则
巩固提升
第四部分
课堂小结
力的
分解
01
02
实例分析
04
正交
分解
03
分类
讨论
力的分解是力的合成的逆运算,力的分解也遵循平行四边形定则。
已知一个确定的合力和一个分力F1的方向和另一个分力F2的大小:
①当 F2< Fsinθ 时,无解;
②当 F2=Fsinθ 时,有唯一解;
③当 Fsinθ
力的正交分解:将力沿两互相垂的方向分解
力的分解的方法:按实际作用效果分解力。
练习1
如图所示,某工人正在修理草坪,推力F与水平方向成α角,则推力在水平方向的分力为( )
A.Fsinα B.Fcosα
C. D.
精选练习
【参考答案:B】
练习2
车载手机支架是一种非常实用的小工具,可将其简化成相互垂直的斜面AB和斜面BC(如图),斜面BC与水平面的夹角为θ,质量为m的手机在两个斜面之间保持静止,重力加速度为g。将重力沿AB、BC方向分解,则沿斜面AB的分力大小为( )
A.mgsinθ B.mgcosθ
C. D.
精选练习
【参考答案:B】
练习3
明朝谢肇淛的《五杂组》中记载:“明姑苏虎丘寺庙倾侧,议欲正之,非万缗不可。一游僧见之,曰:无烦也,我能正之、”游僧每天将木楔从塔身倾斜一侧的砖缝间敲进去,经月余扶正了塔身。假设所用的木楔为等腰三角形,木楔的顶角为θ,现在木楔背上加一力F,方向如图所示,木楔两侧产生推力FN,则( )
A.若F一定,θ大时FN大 B.若F一定,θ小时FN大
C.若θ一定,F大时FN小 D.若θ一定,F小时FN大
精选练习
【参考答案:B】
练习4
如图所示,将力F分解为F1和F2两个分力,若已知F1的大小,F2与F之间的夹角α,且α为锐角。在求解F2大小时( )
A.若F1>Fsinα时,则F2一定有两解
B.若F1=Fsinα时,则F2有唯一解
C.若F1
精选练习
【参考答案:B】
练习5
如图所示,质量为的物体放在水平面上,物体与水平面间的动摩擦因数,g取。当物体做匀速直线运动时,下列说法正确的是( )
A.牵引力F的最小值为
B.牵引力F的最小值为
C.最小牵引力F与水平面的夹角为
D.最小牵引力F与水平面的夹角为
精选练习
【参考答案:D】
解析
分析物体受力情况,受到重力、支持力、拉力、摩擦力,建立直角坐标系进行力的分解,如图所示,根据平衡条件得根据摩擦力的计算公式可得
联立解得
其中则所以F的最小值为
此时,故选D。
精选练习
【参考答案:D】
练习6
同在xOy平面内的六个力如图所示,大小分别为F1=10N,,F3=12N,,F5=30N,F6=12N,求合力的大小和方向。
精选练习
解析
根据平行四边形定则将各力垂直分解到两个坐标轴上,则可得x轴方向的合力为
y轴方向的合力为
所以合力大小为
方向沿x正方向。
精选练习
