4.2平行线分线段成比例(教案)2023-2024学年度北师大版数学九年级上册
文档属性
| 名称 | 4.2平行线分线段成比例(教案)2023-2024学年度北师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 195.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-06 23:02:18 | ||
图片预览

文档简介
2 平行线分线段成比例
教学目标:
1.理解并掌握平行线分线段成比例的基本事实及其推论,并会灵活应用.
2.通过应用,培养识图能力和推理论证能力.
3.培养学生积极地思考、动手、观察的能力,使学生感悟数学知识在生活中的价值,养成合作交流的习惯.
教学重难点:
重点:平行线分线段成比例的推论及其应用.
难点:平行线分线段成比例及推论的灵活应用,平行线分线段成比例的变式.
教学过程:
导入
1.什么叫比例线段
解:四条线段a,b,c,d中,如果a∶b=c∶d,那么这四条线段a,b,c,d叫做成比例的线段,简称比例线段.
2.比例的基本性质
解:如果a∶b=c∶d,那么ad=bc.
如果ad=bc(a,b,c,d都不等于0),
那么a∶b=c∶d.
3.等比性质的内容是什么
解:如果==…=(b+d+…+n≠0),那么 =,
必须保证b+d+…+n≠0,否则结果无意义.
讲授新课
知识点1 平行线分线段成比例
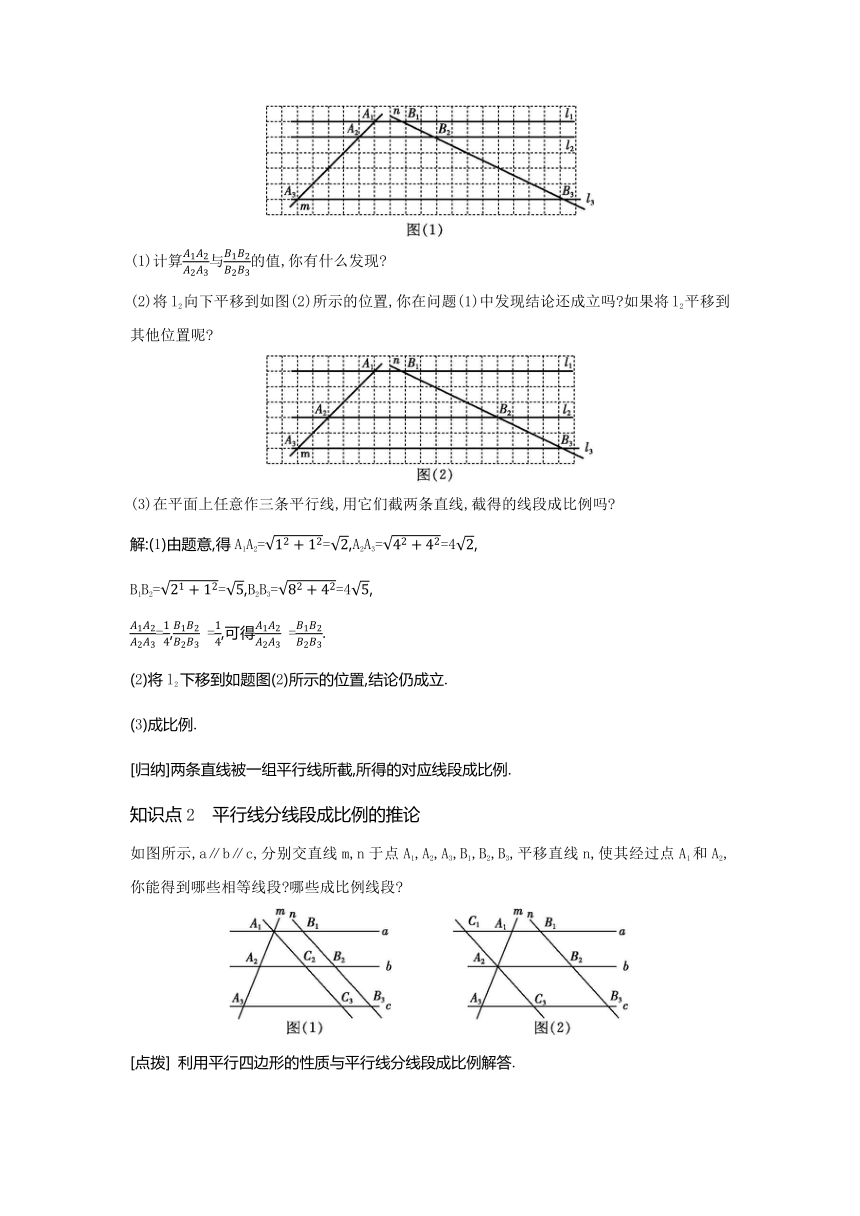
在图(1)中,小方格的边长均为1,直线l1∥l2∥l3,分别交直线m,n于格点A1,A2,A3,B1,B2,B3.
(1)计算与的值,你有什么发现
(2)将l2向下平移到如图(2)所示的位置,你在问题(1)中发现结论还成立吗 如果将l2平移到其他位置呢
(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗
解:(1)由题意,得A1A2==,A2A3==4,
B1B2==,B2B3==4,
=, =,可得 =.
(2)将l2下移到如题图(2)所示的位置,结论仍成立.
(3)成比例.
[归纳]两条直线被一组平行线所截,所得的对应线段成比例.
知识点2 平行线分线段成比例的推论
如图所示,a∥b∥c,分别交直线m,n于点A1,A2,A3,B1,B2,B3,平移直线n,使其经过点A1和A2,你能得到哪些相等线段 哪些成比例线段
[点拨] 利用平行四边形的性质与平行线分线段成比例解答.
解:图(1)中,A1C2=B1B2,C2C3=B2B3,图(2)中,A2C1=B1B2,A2C3=B2B3,
= = , = =等.
[归纳]平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.
范例应用
例1 如图所示,a∥b∥c.直线m,n与a,b,c分别相交于点A,B,C和点D,E,F.若AB∶BC=2∶5.DF=10,求EF的长.
解:因为 =,
所以 =,
因为a∥b∥c,
所以 =.
所以 =.
所以EF=.
例2 如图所示,在△ABC中,D,E在边AB,AC上,DE∥BC,AB=3,AC=4,EC=1,求AD的长度.
解:因为AB=3,AC=4,
EC=1,所以AE=3.
因为DE∥BC,所以 =.
即 =.所以AD=.
课堂训练
1.如图所示,直线l1∥l2∥l3,直线a,b与l1,l2,l3分别交于点A,B,C和点D,E,F.若AB∶BC=2∶3,EF=9,则DE的长是(B)
A.4 B.6 C.7 D.12
第1题图 第2题图 第3题图 第4题图
2.如图所示,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为(B)
A.3 B.4 C.5 D.6
3.如图所示,已知AB∥CD∥EF,它们依次交直线l1,l2于点A,D,F和点B,C,E.如果=,BE=20,那么线段BC的长是 8 .
4.如图所示,BD是△ABC的中线,点E是BC边上一点,AE交BD于点F,若BF=FD,则 = .
5.如图所示,△ABC中,DG∥EC,EG∥BC,求证:=.
证明:因为DG∥EC,
所以 =.
因为EG∥BC,
所以 =.
所以=.
小结
1.平行线分线段成比例
(1)基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
(2)应用格式:如图所示,因为l3∥l4∥l5,
所以=,=,=.
2.平行线分线段成比例的推论
(1)平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.
(2)应用格式:如图所示,在三角形中,因为DE∥BC,所以=,=,=.
板书
2 平行线分线段成比例
1.平行线分线段成比例.
2.平行线分线段成比例的推论.
反思
本课时通过让学生动手计算,讨论,总结出平行线分线段成比例的基本事实及推论,在运用推论解题的过程中,学生容易找错对应线段,应引导学生深刻体会平行线分线段成比例的推论的推导过程,体会从特殊到一般的数学思维过程.
教学目标:
1.理解并掌握平行线分线段成比例的基本事实及其推论,并会灵活应用.
2.通过应用,培养识图能力和推理论证能力.
3.培养学生积极地思考、动手、观察的能力,使学生感悟数学知识在生活中的价值,养成合作交流的习惯.
教学重难点:
重点:平行线分线段成比例的推论及其应用.
难点:平行线分线段成比例及推论的灵活应用,平行线分线段成比例的变式.
教学过程:
导入
1.什么叫比例线段
解:四条线段a,b,c,d中,如果a∶b=c∶d,那么这四条线段a,b,c,d叫做成比例的线段,简称比例线段.
2.比例的基本性质
解:如果a∶b=c∶d,那么ad=bc.
如果ad=bc(a,b,c,d都不等于0),
那么a∶b=c∶d.
3.等比性质的内容是什么
解:如果==…=(b+d+…+n≠0),那么 =,
必须保证b+d+…+n≠0,否则结果无意义.
讲授新课
知识点1 平行线分线段成比例
在图(1)中,小方格的边长均为1,直线l1∥l2∥l3,分别交直线m,n于格点A1,A2,A3,B1,B2,B3.
(1)计算与的值,你有什么发现
(2)将l2向下平移到如图(2)所示的位置,你在问题(1)中发现结论还成立吗 如果将l2平移到其他位置呢
(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗
解:(1)由题意,得A1A2==,A2A3==4,
B1B2==,B2B3==4,
=, =,可得 =.
(2)将l2下移到如题图(2)所示的位置,结论仍成立.
(3)成比例.
[归纳]两条直线被一组平行线所截,所得的对应线段成比例.
知识点2 平行线分线段成比例的推论
如图所示,a∥b∥c,分别交直线m,n于点A1,A2,A3,B1,B2,B3,平移直线n,使其经过点A1和A2,你能得到哪些相等线段 哪些成比例线段
[点拨] 利用平行四边形的性质与平行线分线段成比例解答.
解:图(1)中,A1C2=B1B2,C2C3=B2B3,图(2)中,A2C1=B1B2,A2C3=B2B3,
= = , = =等.
[归纳]平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.
范例应用
例1 如图所示,a∥b∥c.直线m,n与a,b,c分别相交于点A,B,C和点D,E,F.若AB∶BC=2∶5.DF=10,求EF的长.
解:因为 =,
所以 =,
因为a∥b∥c,
所以 =.
所以 =.
所以EF=.
例2 如图所示,在△ABC中,D,E在边AB,AC上,DE∥BC,AB=3,AC=4,EC=1,求AD的长度.
解:因为AB=3,AC=4,
EC=1,所以AE=3.
因为DE∥BC,所以 =.
即 =.所以AD=.
课堂训练
1.如图所示,直线l1∥l2∥l3,直线a,b与l1,l2,l3分别交于点A,B,C和点D,E,F.若AB∶BC=2∶3,EF=9,则DE的长是(B)
A.4 B.6 C.7 D.12
第1题图 第2题图 第3题图 第4题图
2.如图所示,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为(B)
A.3 B.4 C.5 D.6
3.如图所示,已知AB∥CD∥EF,它们依次交直线l1,l2于点A,D,F和点B,C,E.如果=,BE=20,那么线段BC的长是 8 .
4.如图所示,BD是△ABC的中线,点E是BC边上一点,AE交BD于点F,若BF=FD,则 = .
5.如图所示,△ABC中,DG∥EC,EG∥BC,求证:=.
证明:因为DG∥EC,
所以 =.
因为EG∥BC,
所以 =.
所以=.
小结
1.平行线分线段成比例
(1)基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
(2)应用格式:如图所示,因为l3∥l4∥l5,
所以=,=,=.
2.平行线分线段成比例的推论
(1)平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.
(2)应用格式:如图所示,在三角形中,因为DE∥BC,所以=,=,=.
板书
2 平行线分线段成比例
1.平行线分线段成比例.
2.平行线分线段成比例的推论.
反思
本课时通过让学生动手计算,讨论,总结出平行线分线段成比例的基本事实及推论,在运用推论解题的过程中,学生容易找错对应线段,应引导学生深刻体会平行线分线段成比例的推论的推导过程,体会从特殊到一般的数学思维过程.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
