函数的概念

课件28张PPT。1.2.1 函数的概念 设在一个变化过程中有两个变量x与y，如果对于x的每一个值，y都有唯一的值与它对应，则称x是自变量，y是x的函数；其中自变量x的取值的集合叫做函数的定义域，和自变量x值对应的y的值叫做函数的值域。初中学习的函数的概念是什么？思考？下面先看几个实例： (1)一枚炮弹发射后，经过26s落到地面击中目标，炮弹的射高为845m，且炮弹距地面的高度h(单位：m)随时间t(单位:s)变化的规律是
h=130t-5t2 (*)
这里，炮弹飞行时间t的变化范围是数集A={t|0≤t≤26},炮弹距地面的高度h的变化范围是数集B ={h|0≤h≤845}.从问题的实际意义可知，对于数集A中的任意一个时间t，按照对应关系(*)，在数集B中都有唯一的高度h和它对应。 (2) 近几十年来，大气中的臭氧迅速减少，因而出现了臭氧层空洞问题。下图中的曲线显示了南极上空臭氧空洞的面积从1979~2001年的变化情况：根据下图中的曲线可知，时间t的变化范围是数集A ={t|1979≤t≤2001}，臭氧层空洞面积S的变化范围是数集B ={S|0≤S≤26}.并且，对于数集A中的每一个时刻t，按照图中的曲线，在数集B中都有唯一确定的臭氧层空洞面积S和它对应. (3) 国际上常用恩格尔系数反映一个国家人民生活质量的高低，恩格尔系数越低，生活质量越高。下表中恩格尔系数随时间(年)变化的情况表明，“八五”计划以来我国城镇居民的生活质量发生了显著变化。 归纳以上三个实例，我们看到，三个实例中变量之间的关系可以描述为：
对于数集A中的每一个x，按照某种对应关系f，在数集B中都有唯一确定的y和它对应，记作
f: A→B. 设A、B是非空数集，如果按照某种对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f: A→B为从集合A到集合B的一个函数，记作
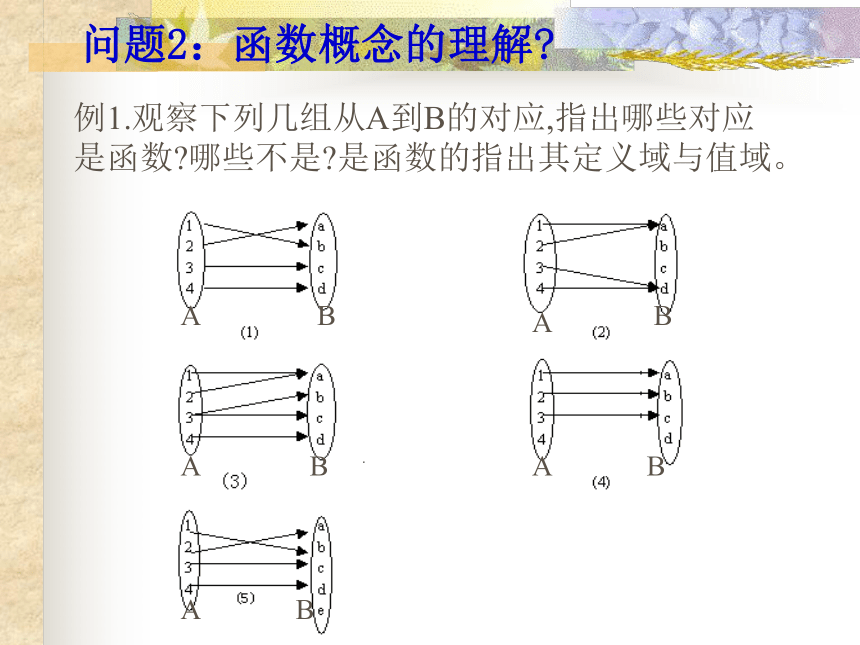
y=f(x),x∈A 其中，x叫做自变量，x的取值范围A叫做函数的定义域；与x的值相对应的y的值叫做函数值，函数值合{f(x)|x∈A}叫做函数的值域。AAABBB 1 2 3 1 2 3 4 5 6 1 1 2 2 3 3 1 4 9 －－－ 1 2 3 4 1 (1)(2)(3)乘2平方求倒数问题2：函数概念的理解?例1.观察下列几组从A到B的对应,指出哪些对应是函数?哪些不是?是函数的指出其定义域与值域。ABABABABAB例2 在下列图象中，请指出哪一个是函数图象，哪一个不是，并说明理由。xxxxyyyyoooo(1)(2)(3)(4)例3下列说法中，不正确的是( )
A、函数值域中的每一个数都有定义域中的一个数与之对应
B、函数的定义域和值域一定是无限集合
C、定义域和对应关系确定后，函数值域也就确定
D、若函数的定义域只有一个元素，则值域也只有一个元素B例4、对于函数y=f(x)，以下说法正确的有( )
①y是x的函数 ②对于不同的x,y的值也不同 ③ f(a)表示当x=a时函数f(x)的值，是一个常量 ④ f(x)一定可以用一个具体的式子表示出来
A、1个 B、2个 C、3个 D、4个B例5、给出四个命题： ①函数就是定义域到值域的对应关系 ②若函数的定义域只含有一个元素，则值域也只有一个元素 ③因f(x)=5(x∈R),这个函数值不随x的变化范围而变化，所以f(0)=5也成立 ④定义域和对应关系确定后，函数值也就确定了 正确有( )
A、1个 B、2个 C、3个 D、4个D练习：P19 2注意⑴ 定义域,值域,对应关系f 称为函数的三要素.B不一定是函数的值域,值域由定义域和对应关系f 确定.例6 下列两个函数是否表示同一个函数？（1） （2） （3）（4）探究问题：两个函数相同需满足的条件是什么？探究小结: 两个函数相同的条件是什么?两函数的定义域和对应法则相同 本课总结：
知识内容:
(1)函数的定义 (2)函数的三要素 (3)两函数相同的条件
思想方法:
(1)数形结合思想 (2)利用举反例来证明命题是错误的方法
探究方式:
(1)从特殊到一般逐步探索，从而解决新问题
(2)从己有知识中利用对比、迁移的方式来解决新问题
设a,b是两个实数，而且a(1)、满足不等式a≤x≤b的实数x的集合叫做闭区间，表示为 [a,b].
(2)、满足不等式a(1)、满足不等式a≤x满足x≥a,x>a,x≤a,x[a, +∞)、(a, +∞)、(-∞，a]、(-∞,a).例1、试用区间表示下列实集：
{x|5 ≤ x<6} (2) {x|x ≥9}
(3) {x|x ≤ -1} ∩{x| -5 ≤ x<2}
(4) {x|x < 9}∪{x| -9 < x<20} 例1求下列函数的定义域
求定义域的几种情况：(1)如果f(x)是整式，那么函数的定义域是实数R (2)如果f(x)是分式，那么函数的定义域是使分母不等于0的实数的集合 (3)如果f(x)是二次根式，那么函数的定义域是使根号内的式子大于或等于0的实数的集合 (4)如果f(x)是由几个部分的数学式子构成的，那么函数的定义域是使各部分式子都有意义的实数集合.（即求各集合的交集）课堂练习求下列函数的定义域
（1）
（2）
（4）
（5）三、函数的值域函数值的集合{f(x)| x∈A }叫做函数的值域 例1、求函数 的值域例2、求函数 的值域 例3求函数的解析式
例1、若函数f(x)的定义域为[1，4]，则函数f(x+2)的定义域为______.[-1,2]练习、若函数y=f(x+1)的定义域为[-2，3]，则y=f(2x-1)的定义域是（ ）。
A、[0，5/2] B、[-1，4]
C、[-5，5] D、[-3，7]作业：
p24 : 1 和 3集合表示区间表示数轴表示{x a＜x＜b}(a , b)。。{x a≤x≤b}[a , b]..{x a≤x＜b}[a , b).。{x a＜x≤b}(a , b].。{x x＜a}(－∞, a)。{x x≤a}(－∞, a].{x x＞b}(b , +∞)。{x x≥b}[b , +∞).{x x∈R}(－∞,+∞)数轴上所有的点