1.2乘、除法的意义和各个部分间的关系(课件)人教版四年级下册数学(共16张PPT)
文档属性
| 名称 | 1.2乘、除法的意义和各个部分间的关系(课件)人教版四年级下册数学(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 711.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-06 19:29:29 | ||
图片预览



文档简介
(共16张PPT)
乘、除法的意义和
各个部分间的关系
四年级下册
第一单元
探究新知
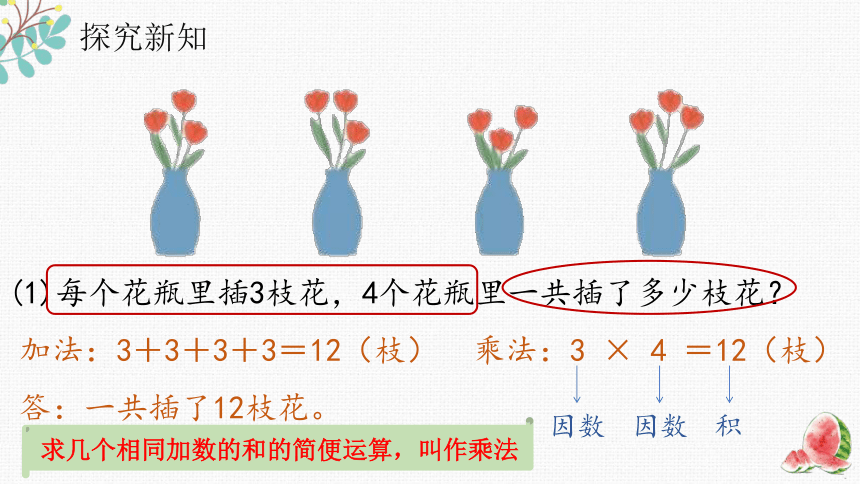
(1)每个花瓶里插3枝花,4个花瓶里一共插了多少枝花?
加法:3+3+3+3=12(枝)
乘法:3 × 4 =12(枝)
答:一共插了12枝花。
因数
因数
积
求几个相同加数的和的简便运算,叫作乘法
探究新知
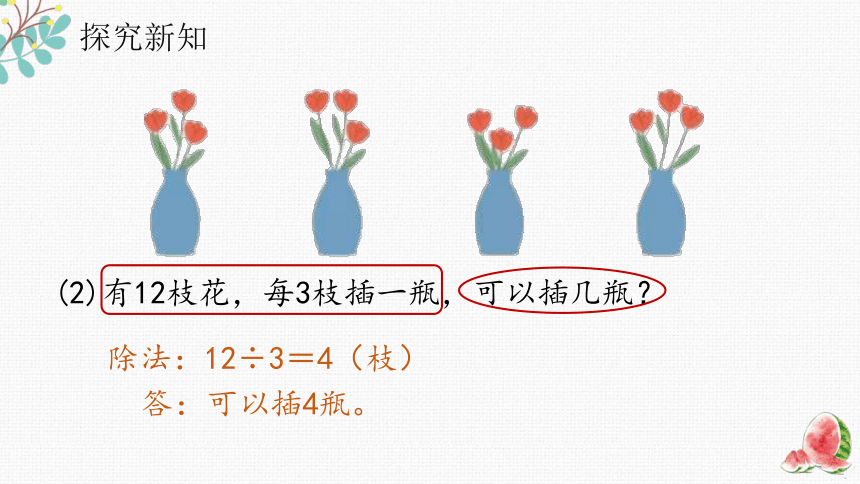
(2)有12枝花,每3枝插一瓶,可以插几瓶?
除法:12÷3=4(枝)
答:可以插4瓶。
探究新知
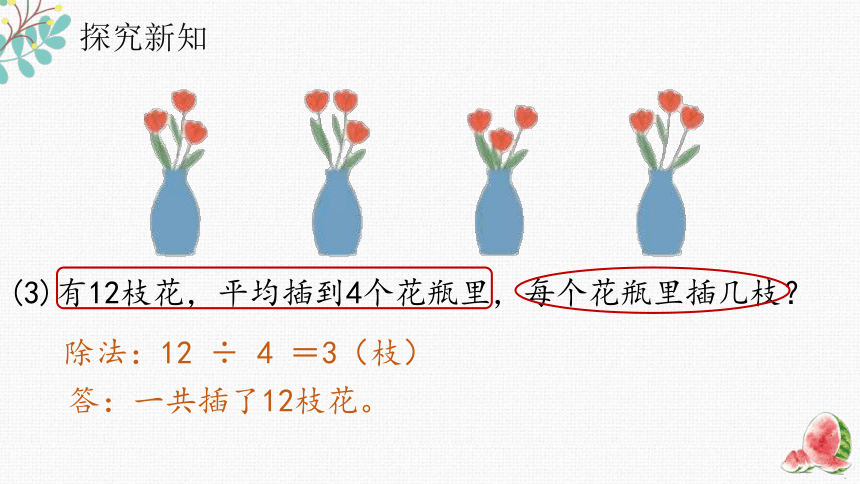
(3)有12枝花,平均插到4个花瓶里,每个花瓶里插几枝?
除法:12 ÷ 4 =3(枝)
答:一共插了12枝花。
探究新知
把(1)3×4=12、(2)12÷3=4和(3)12÷4=3比较,你发现了什么?
3 × 4 = 12
已知两个因数的积与其中一个因数,求另一个因数的运算,叫作除法。
12 ÷ 3 = 4
12 ÷ 4 = 3
积
因数
因数
因数
因数
积
除法是乘法的逆运算
探究新知
12 ÷ 4 = 3
已知的积叫作被除数;
已知的一个因数叫作除数,求得的另一个因数叫作商。
被除数
除数
商
探究新知
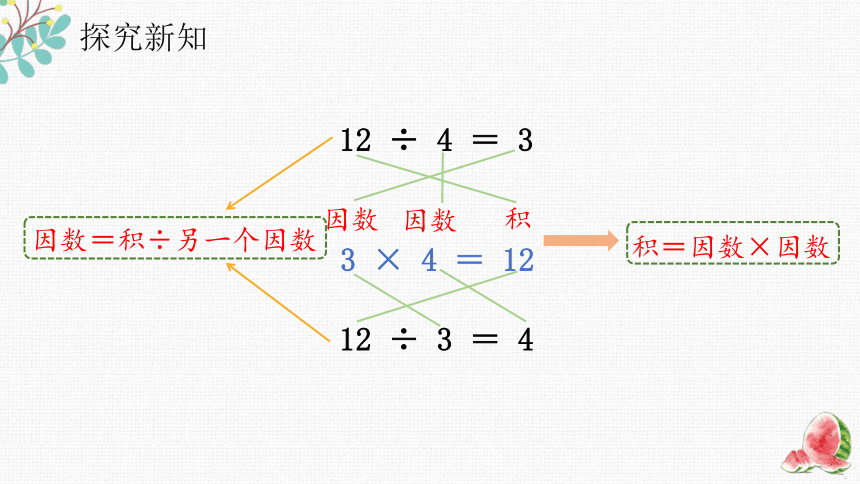
3 × 4 = 12
因数
因数
积
积=因数×因数
12 ÷ 3 = 4
12 ÷ 4 = 3
因数=积÷另一个因数
探究新知
12 ÷ 3 = 4
12 ÷ 4 = 3
被除数
除数
商
被除数
除数
商
商=被除数÷除数
探究新知
12 ÷ 3 = 4
12 ÷ 4 = 3
被除数
除数
商
被除数
除数
商
除数=被除数÷商
12 ÷ 4 = 3
12 ÷ 3 = 4
3 × 4 = 12
3 × 4 = 12
被除数=商×除数
探究新知
在有余数的除法里,被除数与商、除数和余数之间有什么关系?
34 ÷ 5 =6......4
被除数
除数
商
余数
被除数=商×除数+余数
商=(被除数-余数)÷除数
除数=(被除数-余数)÷商
余数=被除数-商×余数
探究新知
观察下列算式,它们有什么共同点?
5+0=5 9-9=0 9×0=0 0×0=0 0÷9=0
(1)在加法中,一个数加上0,还得原数。
(2)在减法中,一个数减去0,还得原数;当被减数等于
减数时,差是0。
(3)在乘法中,一个数和0相乘,仍得0,0乘0得0。
(4)在除法中,0除以一个非0的数,还得0。
有关0的运算:
课堂练习
根据36×14=504,直接写出下面两道题的得数。
504÷14=
504÷36=
36
14
课堂练习
根据乘、除法各个部分间的关系,写出另外两个算式。
28+19=47 47-19=28
47-28=19
203+147=350
17×42=714 714÷17=42
714÷42=17
208×67=13936
1125÷25=45
1008÷38=21
13936÷67=208
13936÷208=67
45×25=1125
1125÷45=25
21×38=1008
1008÷21=38
课堂练习
直接写出得数。
24+0= 13-13= 0×8=
0÷9= 70-0= 0+504=
0÷36= 392×0=
24
0
0
0
70
504
0
392
课堂小结
通过本节课的学习,你有什么收获?
1、乘法各部分间的关系:积=因数×因数;
因数=积÷另一个因数。
2、除法各部分间的关系:
(1)在没有余数的除法里,商=被除数÷除数,
除数=被除数÷商,被除数=商×除数;
(2)在有余数的除法里,被除数=商×除数+余数,
商=(被除数-余数)÷除数,除数=(被除数-余数)÷商,
余数=被除数-商× 除数。
3、乘、除法之间的关系:除法是乘法的逆运算。
感谢观看
四年级下册
第一单元
乘、除法的意义和
各个部分间的关系
四年级下册
第一单元
探究新知
(1)每个花瓶里插3枝花,4个花瓶里一共插了多少枝花?
加法:3+3+3+3=12(枝)
乘法:3 × 4 =12(枝)
答:一共插了12枝花。
因数
因数
积
求几个相同加数的和的简便运算,叫作乘法
探究新知
(2)有12枝花,每3枝插一瓶,可以插几瓶?
除法:12÷3=4(枝)
答:可以插4瓶。
探究新知
(3)有12枝花,平均插到4个花瓶里,每个花瓶里插几枝?
除法:12 ÷ 4 =3(枝)
答:一共插了12枝花。
探究新知
把(1)3×4=12、(2)12÷3=4和(3)12÷4=3比较,你发现了什么?
3 × 4 = 12
已知两个因数的积与其中一个因数,求另一个因数的运算,叫作除法。
12 ÷ 3 = 4
12 ÷ 4 = 3
积
因数
因数
因数
因数
积
除法是乘法的逆运算
探究新知
12 ÷ 4 = 3
已知的积叫作被除数;
已知的一个因数叫作除数,求得的另一个因数叫作商。
被除数
除数
商
探究新知
3 × 4 = 12
因数
因数
积
积=因数×因数
12 ÷ 3 = 4
12 ÷ 4 = 3
因数=积÷另一个因数
探究新知
12 ÷ 3 = 4
12 ÷ 4 = 3
被除数
除数
商
被除数
除数
商
商=被除数÷除数
探究新知
12 ÷ 3 = 4
12 ÷ 4 = 3
被除数
除数
商
被除数
除数
商
除数=被除数÷商
12 ÷ 4 = 3
12 ÷ 3 = 4
3 × 4 = 12
3 × 4 = 12
被除数=商×除数
探究新知
在有余数的除法里,被除数与商、除数和余数之间有什么关系?
34 ÷ 5 =6......4
被除数
除数
商
余数
被除数=商×除数+余数
商=(被除数-余数)÷除数
除数=(被除数-余数)÷商
余数=被除数-商×余数
探究新知
观察下列算式,它们有什么共同点?
5+0=5 9-9=0 9×0=0 0×0=0 0÷9=0
(1)在加法中,一个数加上0,还得原数。
(2)在减法中,一个数减去0,还得原数;当被减数等于
减数时,差是0。
(3)在乘法中,一个数和0相乘,仍得0,0乘0得0。
(4)在除法中,0除以一个非0的数,还得0。
有关0的运算:
课堂练习
根据36×14=504,直接写出下面两道题的得数。
504÷14=
504÷36=
36
14
课堂练习
根据乘、除法各个部分间的关系,写出另外两个算式。
28+19=47 47-19=28
47-28=19
203+147=350
17×42=714 714÷17=42
714÷42=17
208×67=13936
1125÷25=45
1008÷38=21
13936÷67=208
13936÷208=67
45×25=1125
1125÷45=25
21×38=1008
1008÷21=38
课堂练习
直接写出得数。
24+0= 13-13= 0×8=
0÷9= 70-0= 0+504=
0÷36= 392×0=
24
0
0
0
70
504
0
392
课堂小结
通过本节课的学习,你有什么收获?
1、乘法各部分间的关系:积=因数×因数;
因数=积÷另一个因数。
2、除法各部分间的关系:
(1)在没有余数的除法里,商=被除数÷除数,
除数=被除数÷商,被除数=商×除数;
(2)在有余数的除法里,被除数=商×除数+余数,
商=(被除数-余数)÷除数,除数=(被除数-余数)÷商,
余数=被除数-商× 除数。
3、乘、除法之间的关系:除法是乘法的逆运算。
感谢观看
四年级下册
第一单元
