【深圳专用】北师大版八年级上一次函数压轴训练01(含解析)
文档属性
| 名称 | 【深圳专用】北师大版八年级上一次函数压轴训练01(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 833.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 16:19:06 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023年10月23日初二数学作业
学校:___________姓名:___________班级:___________考号:___________
一、解答题
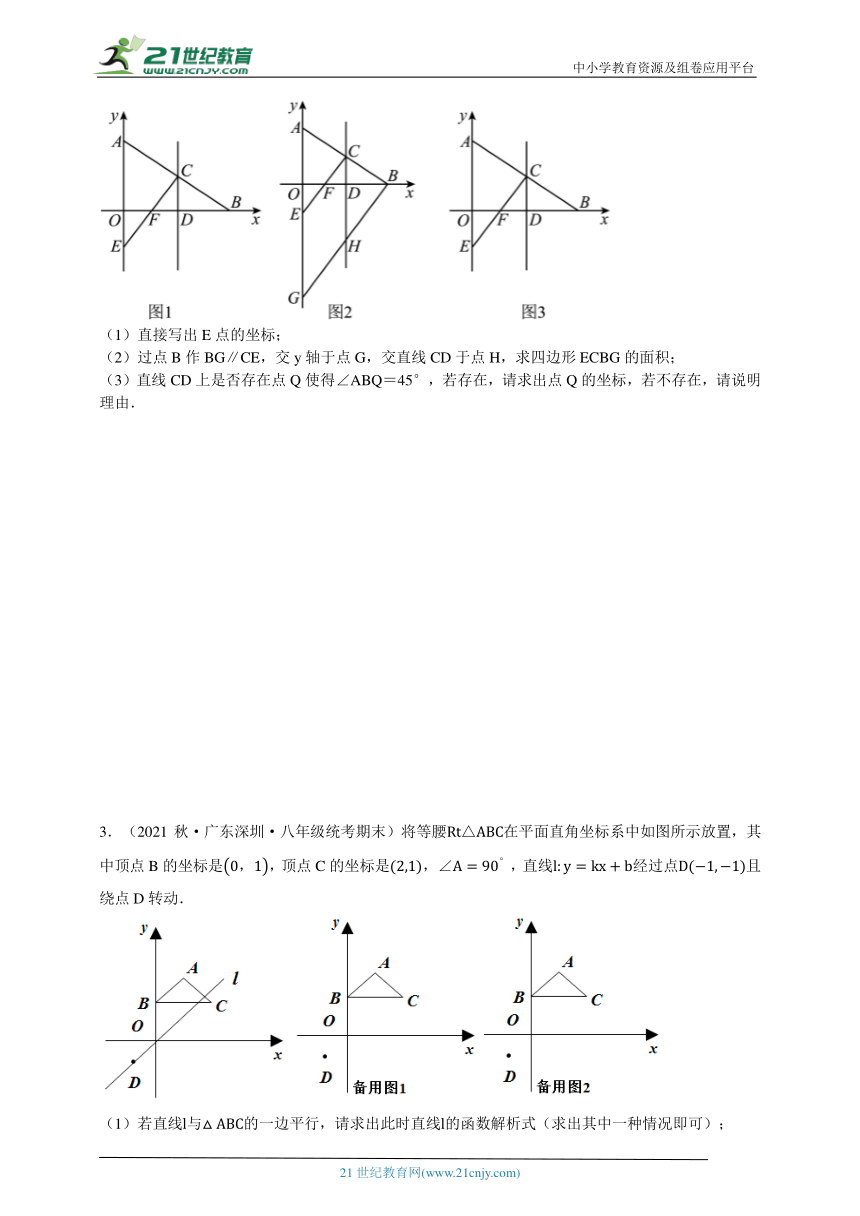
1.(2020秋·广东深圳·八年级深圳第三高中校考期中)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=-x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求点A、点B、点C的坐标,并求出△COB的面积;
(2)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,请求出点P的坐标;
(3)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
2.(2021秋·广东深圳·八年级统考期末)如图,在平面直角坐标系中,A(0,4)、B(6,0)为坐标轴上的点,点C为线段AB的中点,过点C作DC⊥x轴,垂足为D,点E为y轴负半轴上一点,连结CE交x轴于点F,且CF=FE.
(1)直接写出E点的坐标;
(2)过点B作BG∥CE,交y轴于点G,交直线CD于点H,求四边形ECBG的面积;
(3)直线CD上是否存在点Q使得∠ABQ=45°,若存在,请求出点Q的坐标,若不存在,请说明理由.
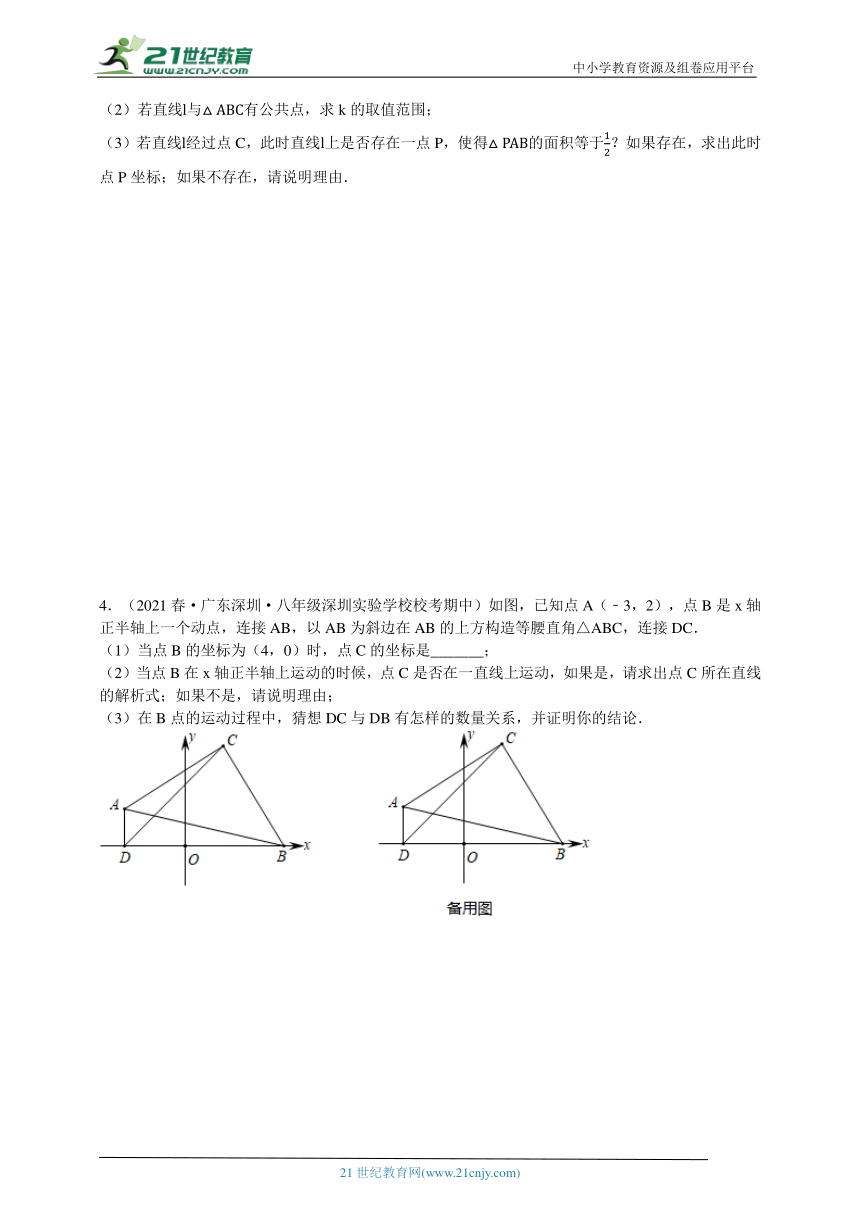
3.(2021秋·广东深圳·八年级统考期末)将等腰在平面直角坐标系中如图所示放置,其中顶点B的坐标是,顶点C的坐标是,直线经过点且绕点D转动.
(1)若直线与的一边平行,请求出此时直线的函数解析式(求出其中一种情况即可);
(2)若直线与有公共点,求k的取值范围;
(3)若直线经过点C,此时直线上是否存在一点P,使得的面积等于?如果存在,求出此时点P坐标;如果不存在,请说明理由.
4.(2021春·广东深圳·八年级深圳实验学校校考期中)如图,已知点A(﹣3,2),点B是x轴正半轴上一个动点,连接AB,以AB为斜边在AB的上方构造等腰直角△ABC,连接DC.
(1)当点B的坐标为(4,0)时,点C的坐标是_______;
(2)当点B在x轴正半轴上运动的时候,点C是否在一直线上运动,如果是,请求出点C所在直线的解析式;如果不是,请说明理由;
(3)在B点的运动过程中,猜想DC与DB有怎样的数量关系,并证明你的结论.
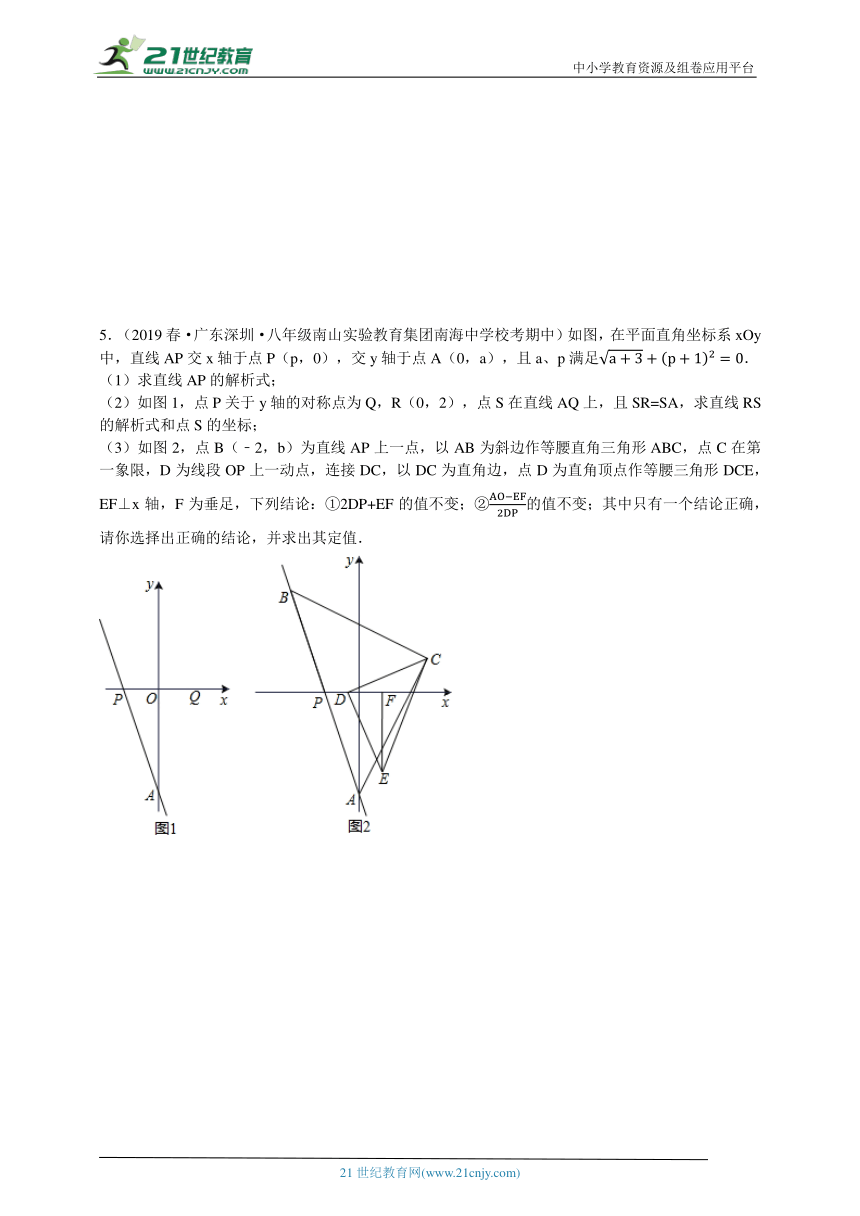
5.(2019春·广东深圳·八年级南山实验教育集团南海中学校考期中)如图,在平面直角坐标系xOy中,直线AP交x轴于点P(p,0),交y轴于点A(0,a),且a、p满足.
(1)求直线AP的解析式;
(2)如图1,点P关于y轴的对称点为Q,R(0,2),点S在直线AQ上,且SR=SA,求直线RS的解析式和点S的坐标;
(3)如图2,点B(﹣2,b)为直线AP上一点,以AB为斜边作等腰直角三角形ABC,点C在第一象限,D为线段OP上一动点,连接DC,以DC为直角边,点D为直角顶点作等腰三角形DCE,EF⊥x轴,F为垂足,下列结论:①2DP+EF的值不变;②的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.
6.(2022秋·广东深圳·八年级校考期中)如图,在平面直角坐标系中,直线y= 2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C.
(1)求点C的坐标.
(2)若P是x轴上的一个动点,直接写出当△POC是等腰三角形时P的坐标.
(3)在直线AB上是否存在点M,使得△MOC的面积是△AOC面积的2倍?若存在,请求出点M的坐标;若不存在,请说明理由.
7.(2019秋·广东深圳·八年级深圳市宝安第一外国语学校校考期中)如图 1,在平面直角坐标系中,直线l1:yx5与x轴,y轴分别交于A.B两点.直线l2:y4xb与l1交于点 D(-3,8)且与x轴,y轴分别交于C、E.
(1)求出点A坐标,直线l2的解析式;
(2)如图2,点P为线段AD上一点(不含端点),连接CP,一动点Q从C出发,沿线段CP 以每秒1个单位的速度运动到点P,再沿着线段PD以每秒个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;
(3)如图3,平面直角坐标系中有一点G(m,2),使得SCEGSCEB,求点G的坐标.
8.(2019春·广东深圳·八年级统考期末)如图1,在平面直角坐标系中,直线y=﹣x+b与x轴、y轴相交于A、B两点,动点C(m,0)在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
(1)求m和b的数量关系;
(2)当m=1时,如图2,将△BCD沿x轴正方向平移得△B′C′D′,当直线B′C′经过点D时,求点B′的坐标及△BCD平移的距离;
(3)在(2)的条件下,直线AB上是否存在一点P,以P、C、D为顶点的三角形是等腰直角三角形?若存在,写出满足条件的P点坐标;若不存在,请说明理由.
9.(2020秋·广东深圳·八年级深圳市高级中学校考期中)模型建立:
(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.
求证:△BEC≌△CDA.
模型应用:
(2)已知直线l1:y=x+4与y轴交于A点,将直线l1绕着A点顺时针旋转45°至l2,如图2,求l2的函数解析式.
(3)如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x-6上的一点,若△APD是不以A为直角顶点的等腰Rt△,请直接写出点D的坐标.
10.(2018秋·广东深圳·八年级校联考期末)如图,在平面直角坐标系中,直线l1的解析式为y=-x,直线l2与l1交于点A(a,-a),与y轴交于点B(0,b),其中a,b满足(a+3)2+=0.
(1)求直线l2的解析式;
(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;
(3)已知平行于y轴左侧有一动直线,分别与l1,l2交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请求出满足条件的点Q的坐标.
11 . 如图1,在平面直角坐标系中将y=2x+1向下平移3个单位长度得到直线,直线与x轴交于点C;直线:y=x+2与x轴、y轴交于A、B两点,且与直线交于点D.
(1)填空:点A的坐标为______,点B的坐标为______;
(2)直线的表达式为______;
(3)在直线上是否存在点E,使?若存在,则求出点E的坐标;若不存在,请说明理由.
(4)如图2,点P为线段AD上一点不含端点,连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.
12 . 如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;
(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.
13. 如图,矩形ABC0位于直角坐标平面,O为原点,A、C分别在坐标轴上,B的坐标为(8,6),线段BC上有一动点P,已知点D在第一象限.
(1)D是直线y=2x+6上一点,若△APD是等腰直角三角形,求点D的坐标;
(2)D是直线y=2x﹣6上一点,若△APD是等腰直角三角形.求点D的坐标.
14 . 建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
实践操作:过点A作AD⊥l于点D,过点B作BE⊥l于点E,求证:△CAD≌△BCE.
模型应用:(1)如图2,在直角坐标系中,直线l1:y= x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
如图,直线y=2x+m与x轴交于点A(-2,0),直线y= -x+n与x轴、y轴分别交于B、C两点,并与直线y=2x+m相交于点D,若AB=4.
(1)、求点D的坐标;
、求出四边形AOCD的面积;
、若E为x轴上一点,且为等腰三角形,写出点E的坐标直接写出答案.
参考答案:
1.(1)点A、B的坐标分别为(6,0),(0,3),点C(2,2);△COB的面积=3;(2)P(4,1);(3)点Q的坐标为(0,)或(0,)或(0,)
【分析】(1)点A、B的坐标分别为(6,0)、(0,3),联立式y=x,y=﹣x+3得:点C(2,2);△COB的面积=,即可求解;
(2)设点P(m,﹣m+3),S△COP=S△COB,则BC=PC,则(m﹣2)2+(﹣m+3﹣2)2=22+12=5,即可求解;
(3)分∠MQN=90°、∠QNM=90°、∠NMQ=90°三种情况,分别求解即可.
【详解】解:(1)直线l2的解析式为y=-x+3,与x轴、y轴分别交于点A、点B,则点A、B的坐标分别为(6,0)、(0,3),
联立式y=x,y=-x+3并解得:x=2,故点C(2,2);
△COB的面积==×3×2=3;
(2)设点P(m,-m+3),
S△COP=S△COB,则BC=PC,
则(m-2)2+(-m+3-2)2=22+12=5,
解得:m=4或0(舍去0),
故点P(4,1);
(3)设点M、N、Q的坐标分别为(m,m)、(m,3-m)、(0,n),
①当∠MQN=90°时,
∵∠GNQ+∠GQN=90°,∠GQN+∠HQM=90°,
∴∠MQH=∠GNQ,∠NGQ=∠QHM=90°,QM=QN,
∴△NGQ≌△QHM(AAS),
∴GN=QH,GQ=HM,
即:m=3-m-n,n-m=m,
解得:m=,n=;
②当∠QNM=90°时,
则MN=QN,即:3-m-m=m,解得:m=,
n==3-;
③当∠NMQ=90°时,
同理可得:n=;
综上,点Q的坐标为(0,)或(0,)或(0,).
【点睛】本题主要考查一次函数与几何的综合,熟练掌握一次函数的性质及等腰三角形的性质是解题的关键.
2.(1)E(0,﹣2);(2)27;(3)存在,点Q的坐标为(3,15)或(3,﹣).
【分析】(1)证明△CDF≌△EOF(AAS),由全等三角形的性质得出CD=OE,由中位线定理求出CD=2,则可得出答案;
(2)过出直线CE的解析式,可求出直线BG的解析式,则求出AG=12,由S四边形ECBG=S△ABG﹣S△ACE可求出答案;
(3)分点Q在x轴的上方或点Q在x轴下方两种情况画出图形,由等腰直角三角形的性质和全等三角形的性质可求出答案.
【详解】解:(1)∵CD⊥x轴,
∴∠CDF=90°=∠EOF,
又∵∠CFD=∠EFO,CF=EF,
∴△CDF≌△EOF(AAS),
∴CD=OE,
又∵A(0,4),B(6,0),
∴OA=4,OB=6,
∵点C为AB的中点,CD∥y轴,
∴CDOA=2,
∴OE=2,
∴E(0,﹣2);
(2)设直线CE的解析式为y=kx+b,
∵C为AB的中点,A(0,4),B(6,0),
∴C(3,2),
∴,
解得,
∴直线CE的解析式为yx﹣2,
∵BG∥CE,
∴设直线BG的解析式为yx+m,
∴6+m=0,
∴m=﹣8,
∴G点的坐标为(0,﹣8),
∴AG=12,
∴S四边形ECBG=S△ABG﹣S△ACE
AE×OD
6×3
=27.
(3)直线CD上存在点Q使得∠ABQ=45°,分两种情况:
如图1,当点Q在x轴的上方时,∠ABQ=45°,
过点A作AM⊥AB,交BQ于点M,过点M作MH⊥y轴于点H,
则△ABM为等腰直角三角形,
∴AM=AB,
∵∠HAM+∠OAB=∠OAB+∠ABO=90°,
∴∠HAM=∠ABO,
∵∠AHM=∠AOB=90°,
∴△AMH≌△BAO(AAS),
∴MH=AO=4,AH=BO=6,
∴OH=AH+OA=6+4=10,
∴M(4,10),
∵B(6,0),
∴直线BM的解析式为y=﹣5x+30,
∵C(3,2),CD∥y轴,
∴C点的横坐标为3,
∴y=﹣5×3+30=15,
∴Q(3,15).
如图2,当点Q在x轴下方时,∠ABQ=45°,
过点A作AN⊥AB,交BQ于点N,过点N作NG⊥y轴于点G,
同理可得△ANG≌△BAO,
∴NG=AO=4,AG=OB=6,
∴N(﹣4,﹣2),
∴直线BN的解析式为yx,
∴Q(3,).
综上所述,点Q的坐标为(3,15)或(3,).
【点睛】本题是综合题,考查了等腰直角三角形的判定与性质,全等三角形的判定与性质,一次函数解析式的求法,四边形的面积,坐标与图形的性质,熟练掌握全等三角形的判定与性质是解题的关键.
3.(1)y=x(答案不唯一);(2)≤k≤2;(3)存在,P(-1,-1)或(-7,-5)
【分析】(1)根据两直线平行,解析式的比例系数相等,再用待定系数法求解即可;
(2)分别求出①当直线l过点B时,②当直线l过点C时,一次函数所对应的比例系数,进而即可得到k的范围;
(3)先求出直线l过点C时的函数解析式,再求出过点P且平行AB的直线解析式,设直线y=x 与y轴的交点为M,表示出BM的长度,过点B作BN⊥PM,表示出MN的长度,进而即可求解.
【详解】(1)∵等腰中,顶点B的坐标是,顶点C的坐标是,
∴点A的横坐标为:(0+2)÷2=1,点A的纵坐标为:1+1=2,
∴A(1,2),
设直线AB的函数解析式为:y=mx+n,
把,(1,2),代入上式得:,解得:,
∴y=x+1,
若 l∥AB时,则k=1,
∵直线经过点,
∴b=0,
∴直线的函数解析式为:y=x(答案不唯一);
(2)①当直线l过点B时,则,解得k=2,
②当直线l过点C时,则,解得:k=,b=
综上所述:直线与有公共点时,≤k≤2;
(3)由(2)可知,当直线l过点C时,k=,b=,
∴y=x,
设P(m,m),
设过点P且平行AB的直线解析式为:y=x+b,
把P(m,m)代入y=x+b,得:m=m+b,解得:b= ,
∴过点P且平行AB的直线解析式为:y=x ,
∴设直线y=x 与y轴的交点为M,则M(0, ),
∴BM=|1-( )|=|+|,
过点B作BN⊥PM,
∵PM∥AB,
∴∠BMP=45°,即 BMN是等腰直角三角形,
∴MN=BM÷=|+|÷=,
∵AB=,
∴的面积=××=,解得:m=-1或-7,
∴P(-1,-1)或(-7,-5).
【点睛】本题主要考查一次函数与平面几何的综合,熟练掌握一次函数的图像和性质,待定系数法,合理的添加辅助线,是解题的关键.
4.(1)(,) (2)是; (3);证明见解析
【分析】(1)设C(m,n)后,由题意得,根据BO=4可以列出关于n的方程,解方程可以得到n的值,再根据m=n-3可以得到m的值,从而得到C的坐标;
(2)把上问的BO=4改为BO=t后,可以把C点坐标用含t的代数式表示出来,消去t后即可得到C点坐标的解析式;
(3)由(2)可以把CD、BD用含t的代数式表示出来,消去t后即可得到BD、CD满足的关系式.
【详解】解:(1)如图,作DF⊥x轴,BE⊥x轴,过C作CP⊥DF,CQ⊥BE
∵
又∠APC=∠CQB=90°,AC=BC,
∴
设C(m,n)
∴DP=n,AP=n-2
即CQ=n-2,PC=BQ=n,BO=MQ=CQ+MC=n-2+n-3=4
∴
(2)设B:(t,0)C(m,n)时,则由上问
OB=MQ= CQ+MC=n-2+n-3=t,
m=MC=n-3=
令x=
∴C在直线上运动,直线解析式为:
(3)由上问当B为(t,0)时C()
∴BD=t-(-3)=t+3,CD=
即CD=,
∴,
∴
【点睛】本题考查利用坐标解决三角形的综合问题,把问题中的点和线段用坐标正确地表示出来是解题关键.
5.(1)y=﹣3x﹣3;(2)S(,﹣), y=﹣3x+2;(3)②;定值为.
【分析】(1)根据非负数的性质列式求出a、p的值,从而得到点A、P的坐标,然后利用待定系数法求直线的解析式;
(2)根据关于y轴的点的对称求出点Q的坐标,再利用待定系数法求出直线AQ的解析式,设出点S的坐标,然后利用两点间的距离公式列式进行计算即可求出点S的坐标,再利用待定系数法求解直线RS的解析式;
(3)根据点B的横坐标为-2,可知点P为AB的中点,然后求出点B得到坐标,连接PC,过点C作CG⊥x轴于点G,利用角角边证明△APO与△PCG全等,根据全等三角形对应边相等可得PG=AO,CG=PO,再根据△DCE是等腰直角三角形,利用角角边证明△CDG与△EDF全等,根据全等三角形对应边相等可得DG=EF,然后用EF表示出DP的长度,然后代入两个结论进行计算即可找出正确的结论并得到定值.
【详解】(1)根据题意得,a+3=0,p+1=0,
解得a=﹣3,p=﹣1,
∴点A、P的坐标分别为A(0,﹣3)、P(﹣1,0),
设直线AP的解析式为y=mx+n,
则,
解得,
∴直线AP的解析式为y=﹣3x﹣3;
(2)根据题意,点Q的坐标为(1,0),
设直线AQ的解析式为y=kx+c,
则,
解得,
∴直线AQ的解析式为y=3x﹣3,
设点S的坐标为(x,3x﹣3),
则SR=,
SA=,
∵SR=SA,
∴=,
解得x=,
∴3x﹣3=3×﹣3=﹣,
∴点S的坐标为S(,﹣),
设直线RS的解析式为y=ex+f,
则,
解得,
∴直线RS的解析式为y=﹣3x+2;
(3)∵点B(﹣2,b),
∴点P为AB的中点,
连接PC,过点C作CG⊥x轴于点G,
∵△ABC是等腰直角三角形,
∴PC=PA=AB,PC⊥AP,
∴∠CPG+∠APO=90°,∠APO+∠PAO=90°,
∴∠CPG=∠PAO,
在△APO与△PCG中,
,
∴△APO≌△PCG(AAS),
∴PG=AO=3,CG=PO,
∵△DCE是等腰直角三角形,
∴CD=DE,∠CDG+∠EDF=90°,
又∵EF⊥x轴,
∴∠DEF+∠EDF=90°,
∴∠CDG=∠DEF,
在△CDG与△EDF中,
,
∴△CDG≌△EDF(AAS),
∴DG=EF,
∴DP=PG﹣DG=3﹣EF,
①2DP+EF=2(3﹣EF)+EF=6﹣EF,
∴2DP+EF的值随点D的变化而变化,不是定值,
②,
的值与点D的变化无关,是定值.
【点睛】本题综合考查了一次函数的问题,待定系数法求直线解析式,非负数的性质,等腰直角三角形的性质,全等三角形的判定与性质,以及关于y轴对称的点的坐标的特点,综合性较强,难度较大,需仔细分析找准问题的突破口.
6.(1)(4,4);(2)(4,0)或(8,0) 或(,0) 或(,0) ;(3)存在,理由见解析,M(8, 4)或(0,12)
【分析】(1)联立两直线解析式成方程组,解方程组即可得出点C的坐标;
(2)分OC=PC,OC=OP,PC=OP三种情况进行讨论;
(3)分两种情况讨论:当M在x轴下方时;当M在x轴上方时.把△MOC的面积是△AOC面积的2倍的数量关系转化为△MOA的面积与△AOC面积的数量关系即可求解.
【详解】解: (1)联立两直线解析式成方程组,得:,
解得:,
∴点C的坐标为(4,4).
(2) 如图, 分三种情况讨论:
OC为腰,当OC=P1C时,
∵C(4,4),
∴P1(8,0);
OC为腰,当OC=OP2= OP3时,
∵C(4,4),
∴OC=,
,;
当P4C=OP4时,设P(x,0),
则x= ,
解得x=4,
∴P4(4,0).
综上所述,P点坐标为P1(8,0),P2(,0),,P4(4,0).
(3)当y=0时,有0= 2x+12,
解得:x=6,
∴点A的坐标为(6,0),
∴OA=6,
∴S△OAC=× 6× 4=12.
设M(x,y),当M在x轴下方时△MOC的面积是△AOC面积的2倍,
∴△MOA的面积等于△AOC的面积,,
∴,
∴y= 4,
∴,
∴x=8,
∴M(8, 4)
当M在x轴上方时△MOC的面积是△AOC面积的2倍,
∴△MOA的面积等于△AOC的面积的3倍,
∴
∴y=12时,
∴,
∴x=0,
∴M(0,12)
综上所述,M(8, 4)或(0,12).
【点睛】本题考查的是一次函数综合题,涉及到一次函数图象上点的坐标问题及等腰三角形的性质和判定等知识,在解答(2)、(3)时要注意进行分类讨论,不要漏解.
7.(1)A(5,0),y4x-4;
(2)8秒, P(-1,6);
(3).
【分析】(1)根据l1解析式,y=0即可求出点A坐标,将D点代入l2解析式并解方程,即可求出l2解析式
(2)根据OA=OB可知ABO和DPQ都为等腰直角三角形,根据路程和速度,可得点Q在整个运动过程中所用的时间为,当C,P,Q三点共线时,t有最小值,根据矩形的判定和性质可以求出P和Q的坐标以及最小时间.
(3)用面积法,用含m的表达式求出,根据SCEGSCEB可以求出G点坐标.
【详解】(1)直线l1:yx5,令y=0,则x=5,
故A(5,0).
将点D(-3,8)代入l2:y4xb,
解得b=-4,
则直线l2的解析式为y4x-4.
∴点A坐标为A(5,0),直线l2的解析式为y4x-4.
(2)如图所示,过P点做y轴平行线PQ,做D点做x轴平行线DQ,PQ与DQ相交于点Q,可知DPQ为等腰直角三角形,.
依题意有
当C,P,Q三点共线时,t有最小值,此时
故点Q在整个运功过程中所用的最少时间是8秒,此时点P的坐标为(-1,6).
(3)如图过G做x轴平行线,交直线CD于点H,过C点做CJ⊥HG.
根据l2的解析式,可得点H(),E(0,-4),C(-1,0)
根据l1的解析式,可得点A(5,0),B(0,5)
则GH=
又SCEGSCEB
所以,解得
故
【点睛】本题考查一次函数的综合题、待定系数法、平行线的性质、等高模型、垂线段最短等性质,解题的关键是灵活运用所学的知识解决问题,学会用转化的思想思考问题,属于压轴题.
8.(1)b=3m;(2)个单位长度;(3)P(0,3)或(2,2)
【分析】(1)易证△BOC≌△CED,可得BO=CE=b,DE=OC=m,可得点D坐标,代入解析式可求m和b的数量关系;
(2)首先求出点D的坐标,再求出直线B′C′的解析式,求出点C′的坐标即可解决问题;
(3)分两种情况讨论,由等腰直角三角形的性质可求点P坐标.
【详解】解:(1)直线y=﹣x+b中,x=0时,y=b,
所以,B(0,b),又C(m,0),
所以,OB=b,OC=m,
在和中
∴点
(2)∵m=1,
∴b=3,点C(1,0),点D(4,1)
∴直线AB解析式为:
设直线BC解析式为:y=ax+3,且过(1,0)
∴0=a+3
∴a=-3
∴直线BC的解析式为y=-3x+3,
设直线B′C′的解析式为y=-3x+c,把D(4,1)代入得到c=13,
∴直线B′C′的解析式为y=-3x+13,
当y=3时,
当y=0时,
∴△BCD平移的距离是个单位.
(3)当∠PCD=90°,PC=CD时,点P与点B重合,
∴点P(0,3)
如图,当∠CPD=90°,PC=PD时,
∵BC=CD,∠BCD=90°,∠CPD=90°
∴BP=PD
∴点P是BD的中点,且点B(0,3),点D(4,1)
∴点P(2,2)
综上所述,点P为(0,3)或(2,2)时,以P、C、D为顶点的三角形是等腰直角三角形.
【点睛】本题考查一次函数综合题、等腰直角三角形的性质、全等三角形的判定和性质、待定系数法等知识,解题的关键是灵活运用待定系数法解决问题,学会用分类讨论的思想思考问题,学会用平移性质解决问题,属于中考压轴题.
9.(1)证明见解析;(2)y=x+4;(3)(4,2),(,),(,).
【分析】(1)先根据△ABC为等腰直角三角形得出CB=CA,再由AAS定理可知△ACD≌△CBE;
(2)过点B作BC⊥AB于点B,交l2于点C,过C作CD⊥x轴于D,根据∠BAC=45°可知△ABC为等腰Rt△,由(1)可知△CBD≌△BAO,由全等三角形的性质得出C点坐标,利用待定系数法求出直线l2的函数解析式即可;
(3)当点D为直角顶点,分点D在矩形AOCB的内部与外部两种情况;点P为直角顶点,显然此时点D位于矩形AOCB的外部,由此可得出结论.
【详解】(1)∵△ABC为等腰直角三角形,
∴CB=CA,
又∵AD⊥CD,BE⊥EC,
∴∠D=∠E=90°,∠ACD+∠BCE=180°-90°=90°,
又∵∠EBC+∠BCE=90°,
∴∠ACD=∠EBC,
在△ACD与△CBE中,
,
∴△ACD≌△EBC(AAS);
(2)过点B作BC⊥AB于点B,交l2于点C,过C作CD⊥x轴于D,
如图1,
∵∠BAC=45°,
∴△ABC为等腰Rt△,
由(1)可知:△CBD≌△BAO,
∴BD=AO,CD=OB,
∵直线l1:y=x+4,
∴A(0,4),B(-3,0),
∴BD=AO=4.CD=OB=3,
∴OD=4+3=7,
∴C(-7,3),
设l2的解析式为y=kx+b(k≠0),
∴,
∴,
∴l2的解析式:y=x+4;
(3)当点D位于直线y=2x-6上时,分两种情况:
①点D为直角顶点,分两种情况:
当点D在矩形AOCB的内部时,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,设D(x,2x-6);
则OE=2x-6,AE=6-(2x-6)=12-2x,DF=EF-DE=8-x;
则△ADE≌△DPF,得DF=AE,即:
12-2x=8-x,x=4;
∴D(4,2);
当点D在矩形AOCB的外部时,设D(x,2x-6);
则OE=2x-6,AE=OE-OA=2x-6-6=2x-12,DF=EF-DE=8-x;
同1可知:△ADE≌△DPF,
∴AE=DF,即:2x-12=8-x,x=;
∴D(,);
②点P为直角顶点,显然此时点D位于矩形AOCB的外部;
设点D(x,2x-6),则CF=2x-6,BF=2x-6-6=2x-12;
同(1)可得,△APB≌△PDF,
∴AB=PF=8,PB=DF=x-8;
∴BF=PF-PB=8-(x-8)=16-x;
联立两个表示BF的式子可得:
2x-12=16-x,即x=;
∴D(,);
综合上面六种情况可得:存在符合条件的等腰直角三角形;
且D点的坐标为:(4,2),(,),(,).
【点睛】考查的是一次函数综合题,涉及到点的坐标、矩形的性质、一次函数的应用、等腰直角三角形以及全等三角形等相关知识的综合应用,需要考虑的情况较多,难度较大.
10.(1)y=x+4;(2)P点坐标为(-1,5)或(-9,5);(3)Q点的坐标为(0,)或(0,)或(0,).
【分析】(1)根据非负数的性质,可得a,b,根据待定系数法,可得函数解析式;
(2)根据平行线间的距离相等,可得Q到AO的距离等于B到AO的距离,根据等底等高的三角形的面积相等,可得S△AOP=S△AOB,根据解方程组,可得P点坐标;
(3)根据等腰直角三角形的性质,可得关于a的方程,根据解方程,可得a,根据平行于x轴直线上点的纵坐标相等,可得答案.
【详解】解:(1)由(a+3)2+=0,得
a=-3,b=4,
即A(-3,3),B(0,4),
设l2的解析式为y=kx+b,将A,B点坐标代入函数解析式,得
,
解得,
l2的解析式为y=x+4;
(2)如图1,
作PB∥AO,P到AO的距离等于B到AO的距离,
S△AOP=S△AOB.
∵PB∥AO,PB过B点(0,4),
∴PB的解析式为y=-x+4或y=-x-4,
又P在直线y=5上,
联立PB及直线y=5,得
-x+4=5或-x-4=5,
解得x=-1或-9,
∴P点坐标为(-1,5)或(-9,5);
(3)设M点的坐标为(a,-a),N(a,a+4),
∵点M在点N的下方,
∴MN=a+4-(-a)=+4,
如图2,
当∠NMQ=90°时,即MQ∥x轴,NM=MQ,+4=-a,
解得a=-,即M(-,),
∴Q(0,);
如图3,
当∠MNQ=90°时,即NQ∥x轴,NM=NQ,+4=-a,
解得a=-,即N(-,),
∴Q(0,),
如图4,
当∠MQN=90°时,即NM∥y轴,MQ=NQ,a+2=-a,
解得a=-,
∴Q(0,).
综上所述:Q点的坐标为(0,)或(0,)或(0,).
【点睛】本题考查了一次函数综合题,解(1)的关键是利用非负数的性质得出a,b的值,又利用了待定系数法;解(2)的关键是利用等底等高的三角形的面积相等得出P在过B点且平行AO的直线上;解(3)的关键是利用等腰直角三角形的性质得出关于a的方程,要分类讨论,以防遗漏.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023年10月23日初二数学作业
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.(2020秋·广东深圳·八年级深圳第三高中校考期中)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=-x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求点A、点B、点C的坐标,并求出△COB的面积;
(2)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,请求出点P的坐标;
(3)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
2.(2021秋·广东深圳·八年级统考期末)如图,在平面直角坐标系中,A(0,4)、B(6,0)为坐标轴上的点,点C为线段AB的中点,过点C作DC⊥x轴,垂足为D,点E为y轴负半轴上一点,连结CE交x轴于点F,且CF=FE.
(1)直接写出E点的坐标;
(2)过点B作BG∥CE,交y轴于点G,交直线CD于点H,求四边形ECBG的面积;
(3)直线CD上是否存在点Q使得∠ABQ=45°,若存在,请求出点Q的坐标,若不存在,请说明理由.
3.(2021秋·广东深圳·八年级统考期末)将等腰在平面直角坐标系中如图所示放置,其中顶点B的坐标是,顶点C的坐标是,直线经过点且绕点D转动.
(1)若直线与的一边平行,请求出此时直线的函数解析式(求出其中一种情况即可);
(2)若直线与有公共点,求k的取值范围;
(3)若直线经过点C,此时直线上是否存在一点P,使得的面积等于?如果存在,求出此时点P坐标;如果不存在,请说明理由.
4.(2021春·广东深圳·八年级深圳实验学校校考期中)如图,已知点A(﹣3,2),点B是x轴正半轴上一个动点,连接AB,以AB为斜边在AB的上方构造等腰直角△ABC,连接DC.
(1)当点B的坐标为(4,0)时,点C的坐标是_______;
(2)当点B在x轴正半轴上运动的时候,点C是否在一直线上运动,如果是,请求出点C所在直线的解析式;如果不是,请说明理由;
(3)在B点的运动过程中,猜想DC与DB有怎样的数量关系,并证明你的结论.
5.(2019春·广东深圳·八年级南山实验教育集团南海中学校考期中)如图,在平面直角坐标系xOy中,直线AP交x轴于点P(p,0),交y轴于点A(0,a),且a、p满足.
(1)求直线AP的解析式;
(2)如图1,点P关于y轴的对称点为Q,R(0,2),点S在直线AQ上,且SR=SA,求直线RS的解析式和点S的坐标;
(3)如图2,点B(﹣2,b)为直线AP上一点,以AB为斜边作等腰直角三角形ABC,点C在第一象限,D为线段OP上一动点,连接DC,以DC为直角边,点D为直角顶点作等腰三角形DCE,EF⊥x轴,F为垂足,下列结论:①2DP+EF的值不变;②的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.
6.(2022秋·广东深圳·八年级校考期中)如图,在平面直角坐标系中,直线y= 2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C.
(1)求点C的坐标.
(2)若P是x轴上的一个动点,直接写出当△POC是等腰三角形时P的坐标.
(3)在直线AB上是否存在点M,使得△MOC的面积是△AOC面积的2倍?若存在,请求出点M的坐标;若不存在,请说明理由.
7.(2019秋·广东深圳·八年级深圳市宝安第一外国语学校校考期中)如图 1,在平面直角坐标系中,直线l1:yx5与x轴,y轴分别交于A.B两点.直线l2:y4xb与l1交于点 D(-3,8)且与x轴,y轴分别交于C、E.
(1)求出点A坐标,直线l2的解析式;
(2)如图2,点P为线段AD上一点(不含端点),连接CP,一动点Q从C出发,沿线段CP 以每秒1个单位的速度运动到点P,再沿着线段PD以每秒个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;
(3)如图3,平面直角坐标系中有一点G(m,2),使得SCEGSCEB,求点G的坐标.
8.(2019春·广东深圳·八年级统考期末)如图1,在平面直角坐标系中,直线y=﹣x+b与x轴、y轴相交于A、B两点,动点C(m,0)在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
(1)求m和b的数量关系;
(2)当m=1时,如图2,将△BCD沿x轴正方向平移得△B′C′D′,当直线B′C′经过点D时,求点B′的坐标及△BCD平移的距离;
(3)在(2)的条件下,直线AB上是否存在一点P,以P、C、D为顶点的三角形是等腰直角三角形?若存在,写出满足条件的P点坐标;若不存在,请说明理由.
9.(2020秋·广东深圳·八年级深圳市高级中学校考期中)模型建立:
(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.
求证:△BEC≌△CDA.
模型应用:
(2)已知直线l1:y=x+4与y轴交于A点,将直线l1绕着A点顺时针旋转45°至l2,如图2,求l2的函数解析式.
(3)如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x-6上的一点,若△APD是不以A为直角顶点的等腰Rt△,请直接写出点D的坐标.
10.(2018秋·广东深圳·八年级校联考期末)如图,在平面直角坐标系中,直线l1的解析式为y=-x,直线l2与l1交于点A(a,-a),与y轴交于点B(0,b),其中a,b满足(a+3)2+=0.
(1)求直线l2的解析式;
(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;
(3)已知平行于y轴左侧有一动直线,分别与l1,l2交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请求出满足条件的点Q的坐标.
11 . 如图1,在平面直角坐标系中将y=2x+1向下平移3个单位长度得到直线,直线与x轴交于点C;直线:y=x+2与x轴、y轴交于A、B两点,且与直线交于点D.
(1)填空:点A的坐标为______,点B的坐标为______;
(2)直线的表达式为______;
(3)在直线上是否存在点E,使?若存在,则求出点E的坐标;若不存在,请说明理由.
(4)如图2,点P为线段AD上一点不含端点,连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.
12 . 如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;
(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.
13. 如图,矩形ABC0位于直角坐标平面,O为原点,A、C分别在坐标轴上,B的坐标为(8,6),线段BC上有一动点P,已知点D在第一象限.
(1)D是直线y=2x+6上一点,若△APD是等腰直角三角形,求点D的坐标;
(2)D是直线y=2x﹣6上一点,若△APD是等腰直角三角形.求点D的坐标.
14 . 建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
实践操作:过点A作AD⊥l于点D,过点B作BE⊥l于点E,求证:△CAD≌△BCE.
模型应用:(1)如图2,在直角坐标系中,直线l1:y= x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
如图,直线y=2x+m与x轴交于点A(-2,0),直线y= -x+n与x轴、y轴分别交于B、C两点,并与直线y=2x+m相交于点D,若AB=4.
(1)、求点D的坐标;
、求出四边形AOCD的面积;
、若E为x轴上一点,且为等腰三角形,写出点E的坐标直接写出答案.
参考答案:
1.(1)点A、B的坐标分别为(6,0),(0,3),点C(2,2);△COB的面积=3;(2)P(4,1);(3)点Q的坐标为(0,)或(0,)或(0,)
【分析】(1)点A、B的坐标分别为(6,0)、(0,3),联立式y=x,y=﹣x+3得:点C(2,2);△COB的面积=,即可求解;
(2)设点P(m,﹣m+3),S△COP=S△COB,则BC=PC,则(m﹣2)2+(﹣m+3﹣2)2=22+12=5,即可求解;
(3)分∠MQN=90°、∠QNM=90°、∠NMQ=90°三种情况,分别求解即可.
【详解】解:(1)直线l2的解析式为y=-x+3,与x轴、y轴分别交于点A、点B,则点A、B的坐标分别为(6,0)、(0,3),
联立式y=x,y=-x+3并解得:x=2,故点C(2,2);
△COB的面积==×3×2=3;
(2)设点P(m,-m+3),
S△COP=S△COB,则BC=PC,
则(m-2)2+(-m+3-2)2=22+12=5,
解得:m=4或0(舍去0),
故点P(4,1);
(3)设点M、N、Q的坐标分别为(m,m)、(m,3-m)、(0,n),
①当∠MQN=90°时,
∵∠GNQ+∠GQN=90°,∠GQN+∠HQM=90°,
∴∠MQH=∠GNQ,∠NGQ=∠QHM=90°,QM=QN,
∴△NGQ≌△QHM(AAS),
∴GN=QH,GQ=HM,
即:m=3-m-n,n-m=m,
解得:m=,n=;
②当∠QNM=90°时,
则MN=QN,即:3-m-m=m,解得:m=,
n==3-;
③当∠NMQ=90°时,
同理可得:n=;
综上,点Q的坐标为(0,)或(0,)或(0,).
【点睛】本题主要考查一次函数与几何的综合,熟练掌握一次函数的性质及等腰三角形的性质是解题的关键.
2.(1)E(0,﹣2);(2)27;(3)存在,点Q的坐标为(3,15)或(3,﹣).
【分析】(1)证明△CDF≌△EOF(AAS),由全等三角形的性质得出CD=OE,由中位线定理求出CD=2,则可得出答案;
(2)过出直线CE的解析式,可求出直线BG的解析式,则求出AG=12,由S四边形ECBG=S△ABG﹣S△ACE可求出答案;
(3)分点Q在x轴的上方或点Q在x轴下方两种情况画出图形,由等腰直角三角形的性质和全等三角形的性质可求出答案.
【详解】解:(1)∵CD⊥x轴,
∴∠CDF=90°=∠EOF,
又∵∠CFD=∠EFO,CF=EF,
∴△CDF≌△EOF(AAS),
∴CD=OE,
又∵A(0,4),B(6,0),
∴OA=4,OB=6,
∵点C为AB的中点,CD∥y轴,
∴CDOA=2,
∴OE=2,
∴E(0,﹣2);
(2)设直线CE的解析式为y=kx+b,
∵C为AB的中点,A(0,4),B(6,0),
∴C(3,2),
∴,
解得,
∴直线CE的解析式为yx﹣2,
∵BG∥CE,
∴设直线BG的解析式为yx+m,
∴6+m=0,
∴m=﹣8,
∴G点的坐标为(0,﹣8),
∴AG=12,
∴S四边形ECBG=S△ABG﹣S△ACE
AE×OD
6×3
=27.
(3)直线CD上存在点Q使得∠ABQ=45°,分两种情况:
如图1,当点Q在x轴的上方时,∠ABQ=45°,
过点A作AM⊥AB,交BQ于点M,过点M作MH⊥y轴于点H,
则△ABM为等腰直角三角形,
∴AM=AB,
∵∠HAM+∠OAB=∠OAB+∠ABO=90°,
∴∠HAM=∠ABO,
∵∠AHM=∠AOB=90°,
∴△AMH≌△BAO(AAS),
∴MH=AO=4,AH=BO=6,
∴OH=AH+OA=6+4=10,
∴M(4,10),
∵B(6,0),
∴直线BM的解析式为y=﹣5x+30,
∵C(3,2),CD∥y轴,
∴C点的横坐标为3,
∴y=﹣5×3+30=15,
∴Q(3,15).
如图2,当点Q在x轴下方时,∠ABQ=45°,
过点A作AN⊥AB,交BQ于点N,过点N作NG⊥y轴于点G,
同理可得△ANG≌△BAO,
∴NG=AO=4,AG=OB=6,
∴N(﹣4,﹣2),
∴直线BN的解析式为yx,
∴Q(3,).
综上所述,点Q的坐标为(3,15)或(3,).
【点睛】本题是综合题,考查了等腰直角三角形的判定与性质,全等三角形的判定与性质,一次函数解析式的求法,四边形的面积,坐标与图形的性质,熟练掌握全等三角形的判定与性质是解题的关键.
3.(1)y=x(答案不唯一);(2)≤k≤2;(3)存在,P(-1,-1)或(-7,-5)
【分析】(1)根据两直线平行,解析式的比例系数相等,再用待定系数法求解即可;
(2)分别求出①当直线l过点B时,②当直线l过点C时,一次函数所对应的比例系数,进而即可得到k的范围;
(3)先求出直线l过点C时的函数解析式,再求出过点P且平行AB的直线解析式,设直线y=x 与y轴的交点为M,表示出BM的长度,过点B作BN⊥PM,表示出MN的长度,进而即可求解.
【详解】(1)∵等腰中,顶点B的坐标是,顶点C的坐标是,
∴点A的横坐标为:(0+2)÷2=1,点A的纵坐标为:1+1=2,
∴A(1,2),
设直线AB的函数解析式为:y=mx+n,
把,(1,2),代入上式得:,解得:,
∴y=x+1,
若 l∥AB时,则k=1,
∵直线经过点,
∴b=0,
∴直线的函数解析式为:y=x(答案不唯一);
(2)①当直线l过点B时,则,解得k=2,
②当直线l过点C时,则,解得:k=,b=
综上所述:直线与有公共点时,≤k≤2;
(3)由(2)可知,当直线l过点C时,k=,b=,
∴y=x,
设P(m,m),
设过点P且平行AB的直线解析式为:y=x+b,
把P(m,m)代入y=x+b,得:m=m+b,解得:b= ,
∴过点P且平行AB的直线解析式为:y=x ,
∴设直线y=x 与y轴的交点为M,则M(0, ),
∴BM=|1-( )|=|+|,
过点B作BN⊥PM,
∵PM∥AB,
∴∠BMP=45°,即 BMN是等腰直角三角形,
∴MN=BM÷=|+|÷=,
∵AB=,
∴的面积=××=,解得:m=-1或-7,
∴P(-1,-1)或(-7,-5).
【点睛】本题主要考查一次函数与平面几何的综合,熟练掌握一次函数的图像和性质,待定系数法,合理的添加辅助线,是解题的关键.
4.(1)(,) (2)是; (3);证明见解析
【分析】(1)设C(m,n)后,由题意得,根据BO=4可以列出关于n的方程,解方程可以得到n的值,再根据m=n-3可以得到m的值,从而得到C的坐标;
(2)把上问的BO=4改为BO=t后,可以把C点坐标用含t的代数式表示出来,消去t后即可得到C点坐标的解析式;
(3)由(2)可以把CD、BD用含t的代数式表示出来,消去t后即可得到BD、CD满足的关系式.
【详解】解:(1)如图,作DF⊥x轴,BE⊥x轴,过C作CP⊥DF,CQ⊥BE
∵
又∠APC=∠CQB=90°,AC=BC,
∴
设C(m,n)
∴DP=n,AP=n-2
即CQ=n-2,PC=BQ=n,BO=MQ=CQ+MC=n-2+n-3=4
∴
(2)设B:(t,0)C(m,n)时,则由上问
OB=MQ= CQ+MC=n-2+n-3=t,
m=MC=n-3=
令x=
∴C在直线上运动,直线解析式为:
(3)由上问当B为(t,0)时C()
∴BD=t-(-3)=t+3,CD=
即CD=,
∴,
∴
【点睛】本题考查利用坐标解决三角形的综合问题,把问题中的点和线段用坐标正确地表示出来是解题关键.
5.(1)y=﹣3x﹣3;(2)S(,﹣), y=﹣3x+2;(3)②;定值为.
【分析】(1)根据非负数的性质列式求出a、p的值,从而得到点A、P的坐标,然后利用待定系数法求直线的解析式;
(2)根据关于y轴的点的对称求出点Q的坐标,再利用待定系数法求出直线AQ的解析式,设出点S的坐标,然后利用两点间的距离公式列式进行计算即可求出点S的坐标,再利用待定系数法求解直线RS的解析式;
(3)根据点B的横坐标为-2,可知点P为AB的中点,然后求出点B得到坐标,连接PC,过点C作CG⊥x轴于点G,利用角角边证明△APO与△PCG全等,根据全等三角形对应边相等可得PG=AO,CG=PO,再根据△DCE是等腰直角三角形,利用角角边证明△CDG与△EDF全等,根据全等三角形对应边相等可得DG=EF,然后用EF表示出DP的长度,然后代入两个结论进行计算即可找出正确的结论并得到定值.
【详解】(1)根据题意得,a+3=0,p+1=0,
解得a=﹣3,p=﹣1,
∴点A、P的坐标分别为A(0,﹣3)、P(﹣1,0),
设直线AP的解析式为y=mx+n,
则,
解得,
∴直线AP的解析式为y=﹣3x﹣3;
(2)根据题意,点Q的坐标为(1,0),
设直线AQ的解析式为y=kx+c,
则,
解得,
∴直线AQ的解析式为y=3x﹣3,
设点S的坐标为(x,3x﹣3),
则SR=,
SA=,
∵SR=SA,
∴=,
解得x=,
∴3x﹣3=3×﹣3=﹣,
∴点S的坐标为S(,﹣),
设直线RS的解析式为y=ex+f,
则,
解得,
∴直线RS的解析式为y=﹣3x+2;
(3)∵点B(﹣2,b),
∴点P为AB的中点,
连接PC,过点C作CG⊥x轴于点G,
∵△ABC是等腰直角三角形,
∴PC=PA=AB,PC⊥AP,
∴∠CPG+∠APO=90°,∠APO+∠PAO=90°,
∴∠CPG=∠PAO,
在△APO与△PCG中,
,
∴△APO≌△PCG(AAS),
∴PG=AO=3,CG=PO,
∵△DCE是等腰直角三角形,
∴CD=DE,∠CDG+∠EDF=90°,
又∵EF⊥x轴,
∴∠DEF+∠EDF=90°,
∴∠CDG=∠DEF,
在△CDG与△EDF中,
,
∴△CDG≌△EDF(AAS),
∴DG=EF,
∴DP=PG﹣DG=3﹣EF,
①2DP+EF=2(3﹣EF)+EF=6﹣EF,
∴2DP+EF的值随点D的变化而变化,不是定值,
②,
的值与点D的变化无关,是定值.
【点睛】本题综合考查了一次函数的问题,待定系数法求直线解析式,非负数的性质,等腰直角三角形的性质,全等三角形的判定与性质,以及关于y轴对称的点的坐标的特点,综合性较强,难度较大,需仔细分析找准问题的突破口.
6.(1)(4,4);(2)(4,0)或(8,0) 或(,0) 或(,0) ;(3)存在,理由见解析,M(8, 4)或(0,12)
【分析】(1)联立两直线解析式成方程组,解方程组即可得出点C的坐标;
(2)分OC=PC,OC=OP,PC=OP三种情况进行讨论;
(3)分两种情况讨论:当M在x轴下方时;当M在x轴上方时.把△MOC的面积是△AOC面积的2倍的数量关系转化为△MOA的面积与△AOC面积的数量关系即可求解.
【详解】解: (1)联立两直线解析式成方程组,得:,
解得:,
∴点C的坐标为(4,4).
(2) 如图, 分三种情况讨论:
OC为腰,当OC=P1C时,
∵C(4,4),
∴P1(8,0);
OC为腰,当OC=OP2= OP3时,
∵C(4,4),
∴OC=,
,;
当P4C=OP4时,设P(x,0),
则x= ,
解得x=4,
∴P4(4,0).
综上所述,P点坐标为P1(8,0),P2(,0),,P4(4,0).
(3)当y=0时,有0= 2x+12,
解得:x=6,
∴点A的坐标为(6,0),
∴OA=6,
∴S△OAC=× 6× 4=12.
设M(x,y),当M在x轴下方时△MOC的面积是△AOC面积的2倍,
∴△MOA的面积等于△AOC的面积,,
∴,
∴y= 4,
∴,
∴x=8,
∴M(8, 4)
当M在x轴上方时△MOC的面积是△AOC面积的2倍,
∴△MOA的面积等于△AOC的面积的3倍,
∴
∴y=12时,
∴,
∴x=0,
∴M(0,12)
综上所述,M(8, 4)或(0,12).
【点睛】本题考查的是一次函数综合题,涉及到一次函数图象上点的坐标问题及等腰三角形的性质和判定等知识,在解答(2)、(3)时要注意进行分类讨论,不要漏解.
7.(1)A(5,0),y4x-4;
(2)8秒, P(-1,6);
(3).
【分析】(1)根据l1解析式,y=0即可求出点A坐标,将D点代入l2解析式并解方程,即可求出l2解析式
(2)根据OA=OB可知ABO和DPQ都为等腰直角三角形,根据路程和速度,可得点Q在整个运动过程中所用的时间为,当C,P,Q三点共线时,t有最小值,根据矩形的判定和性质可以求出P和Q的坐标以及最小时间.
(3)用面积法,用含m的表达式求出,根据SCEGSCEB可以求出G点坐标.
【详解】(1)直线l1:yx5,令y=0,则x=5,
故A(5,0).
将点D(-3,8)代入l2:y4xb,
解得b=-4,
则直线l2的解析式为y4x-4.
∴点A坐标为A(5,0),直线l2的解析式为y4x-4.
(2)如图所示,过P点做y轴平行线PQ,做D点做x轴平行线DQ,PQ与DQ相交于点Q,可知DPQ为等腰直角三角形,.
依题意有
当C,P,Q三点共线时,t有最小值,此时
故点Q在整个运功过程中所用的最少时间是8秒,此时点P的坐标为(-1,6).
(3)如图过G做x轴平行线,交直线CD于点H,过C点做CJ⊥HG.
根据l2的解析式,可得点H(),E(0,-4),C(-1,0)
根据l1的解析式,可得点A(5,0),B(0,5)
则GH=
又SCEGSCEB
所以,解得
故
【点睛】本题考查一次函数的综合题、待定系数法、平行线的性质、等高模型、垂线段最短等性质,解题的关键是灵活运用所学的知识解决问题,学会用转化的思想思考问题,属于压轴题.
8.(1)b=3m;(2)个单位长度;(3)P(0,3)或(2,2)
【分析】(1)易证△BOC≌△CED,可得BO=CE=b,DE=OC=m,可得点D坐标,代入解析式可求m和b的数量关系;
(2)首先求出点D的坐标,再求出直线B′C′的解析式,求出点C′的坐标即可解决问题;
(3)分两种情况讨论,由等腰直角三角形的性质可求点P坐标.
【详解】解:(1)直线y=﹣x+b中,x=0时,y=b,
所以,B(0,b),又C(m,0),
所以,OB=b,OC=m,
在和中
∴点
(2)∵m=1,
∴b=3,点C(1,0),点D(4,1)
∴直线AB解析式为:
设直线BC解析式为:y=ax+3,且过(1,0)
∴0=a+3
∴a=-3
∴直线BC的解析式为y=-3x+3,
设直线B′C′的解析式为y=-3x+c,把D(4,1)代入得到c=13,
∴直线B′C′的解析式为y=-3x+13,
当y=3时,
当y=0时,
∴△BCD平移的距离是个单位.
(3)当∠PCD=90°,PC=CD时,点P与点B重合,
∴点P(0,3)
如图,当∠CPD=90°,PC=PD时,
∵BC=CD,∠BCD=90°,∠CPD=90°
∴BP=PD
∴点P是BD的中点,且点B(0,3),点D(4,1)
∴点P(2,2)
综上所述,点P为(0,3)或(2,2)时,以P、C、D为顶点的三角形是等腰直角三角形.
【点睛】本题考查一次函数综合题、等腰直角三角形的性质、全等三角形的判定和性质、待定系数法等知识,解题的关键是灵活运用待定系数法解决问题,学会用分类讨论的思想思考问题,学会用平移性质解决问题,属于中考压轴题.
9.(1)证明见解析;(2)y=x+4;(3)(4,2),(,),(,).
【分析】(1)先根据△ABC为等腰直角三角形得出CB=CA,再由AAS定理可知△ACD≌△CBE;
(2)过点B作BC⊥AB于点B,交l2于点C,过C作CD⊥x轴于D,根据∠BAC=45°可知△ABC为等腰Rt△,由(1)可知△CBD≌△BAO,由全等三角形的性质得出C点坐标,利用待定系数法求出直线l2的函数解析式即可;
(3)当点D为直角顶点,分点D在矩形AOCB的内部与外部两种情况;点P为直角顶点,显然此时点D位于矩形AOCB的外部,由此可得出结论.
【详解】(1)∵△ABC为等腰直角三角形,
∴CB=CA,
又∵AD⊥CD,BE⊥EC,
∴∠D=∠E=90°,∠ACD+∠BCE=180°-90°=90°,
又∵∠EBC+∠BCE=90°,
∴∠ACD=∠EBC,
在△ACD与△CBE中,
,
∴△ACD≌△EBC(AAS);
(2)过点B作BC⊥AB于点B,交l2于点C,过C作CD⊥x轴于D,
如图1,
∵∠BAC=45°,
∴△ABC为等腰Rt△,
由(1)可知:△CBD≌△BAO,
∴BD=AO,CD=OB,
∵直线l1:y=x+4,
∴A(0,4),B(-3,0),
∴BD=AO=4.CD=OB=3,
∴OD=4+3=7,
∴C(-7,3),
设l2的解析式为y=kx+b(k≠0),
∴,
∴,
∴l2的解析式:y=x+4;
(3)当点D位于直线y=2x-6上时,分两种情况:
①点D为直角顶点,分两种情况:
当点D在矩形AOCB的内部时,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,设D(x,2x-6);
则OE=2x-6,AE=6-(2x-6)=12-2x,DF=EF-DE=8-x;
则△ADE≌△DPF,得DF=AE,即:
12-2x=8-x,x=4;
∴D(4,2);
当点D在矩形AOCB的外部时,设D(x,2x-6);
则OE=2x-6,AE=OE-OA=2x-6-6=2x-12,DF=EF-DE=8-x;
同1可知:△ADE≌△DPF,
∴AE=DF,即:2x-12=8-x,x=;
∴D(,);
②点P为直角顶点,显然此时点D位于矩形AOCB的外部;
设点D(x,2x-6),则CF=2x-6,BF=2x-6-6=2x-12;
同(1)可得,△APB≌△PDF,
∴AB=PF=8,PB=DF=x-8;
∴BF=PF-PB=8-(x-8)=16-x;
联立两个表示BF的式子可得:
2x-12=16-x,即x=;
∴D(,);
综合上面六种情况可得:存在符合条件的等腰直角三角形;
且D点的坐标为:(4,2),(,),(,).
【点睛】考查的是一次函数综合题,涉及到点的坐标、矩形的性质、一次函数的应用、等腰直角三角形以及全等三角形等相关知识的综合应用,需要考虑的情况较多,难度较大.
10.(1)y=x+4;(2)P点坐标为(-1,5)或(-9,5);(3)Q点的坐标为(0,)或(0,)或(0,).
【分析】(1)根据非负数的性质,可得a,b,根据待定系数法,可得函数解析式;
(2)根据平行线间的距离相等,可得Q到AO的距离等于B到AO的距离,根据等底等高的三角形的面积相等,可得S△AOP=S△AOB,根据解方程组,可得P点坐标;
(3)根据等腰直角三角形的性质,可得关于a的方程,根据解方程,可得a,根据平行于x轴直线上点的纵坐标相等,可得答案.
【详解】解:(1)由(a+3)2+=0,得
a=-3,b=4,
即A(-3,3),B(0,4),
设l2的解析式为y=kx+b,将A,B点坐标代入函数解析式,得
,
解得,
l2的解析式为y=x+4;
(2)如图1,
作PB∥AO,P到AO的距离等于B到AO的距离,
S△AOP=S△AOB.
∵PB∥AO,PB过B点(0,4),
∴PB的解析式为y=-x+4或y=-x-4,
又P在直线y=5上,
联立PB及直线y=5,得
-x+4=5或-x-4=5,
解得x=-1或-9,
∴P点坐标为(-1,5)或(-9,5);
(3)设M点的坐标为(a,-a),N(a,a+4),
∵点M在点N的下方,
∴MN=a+4-(-a)=+4,
如图2,
当∠NMQ=90°时,即MQ∥x轴,NM=MQ,+4=-a,
解得a=-,即M(-,),
∴Q(0,);
如图3,
当∠MNQ=90°时,即NQ∥x轴,NM=NQ,+4=-a,
解得a=-,即N(-,),
∴Q(0,),
如图4,
当∠MQN=90°时,即NM∥y轴,MQ=NQ,a+2=-a,
解得a=-,
∴Q(0,).
综上所述:Q点的坐标为(0,)或(0,)或(0,).
【点睛】本题考查了一次函数综合题,解(1)的关键是利用非负数的性质得出a,b的值,又利用了待定系数法;解(2)的关键是利用等底等高的三角形的面积相等得出P在过B点且平行AO的直线上;解(3)的关键是利用等腰直角三角形的性质得出关于a的方程,要分类讨论,以防遗漏.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
