全等三角形复习课
图片预览






文档简介
课件41张PPT。全等三角形的应用将两个全等的等边三角形△ABC和△ACD如图所示
拼在一起,把含60°角的三角板与这个图形重合,使
三角板的60°角的顶点与点A重合,两边分别与AB、
AC重合。将三角板绕点A按逆时针方向旋转。
(1)当三角板的两边分别与两边BC、CD相交于
点E、F时,如图,通过观察或根据定义你能得
出图中有哪几对三角形全等?并说明理由。
ABECDF将两个全等的等边三角形△ABC和△ACD如图所示
拼在一起,把含60°角的三角板与这个图形重合,使
三角板的60°角的顶点与点A重合,两边分别与AB、
AC重合。将三角板绕点A按逆时针方向旋转。
(2)当三角板两边分别与两边BC、CD的延长线
相交于E、F时,如图,你在①中得出的结论还
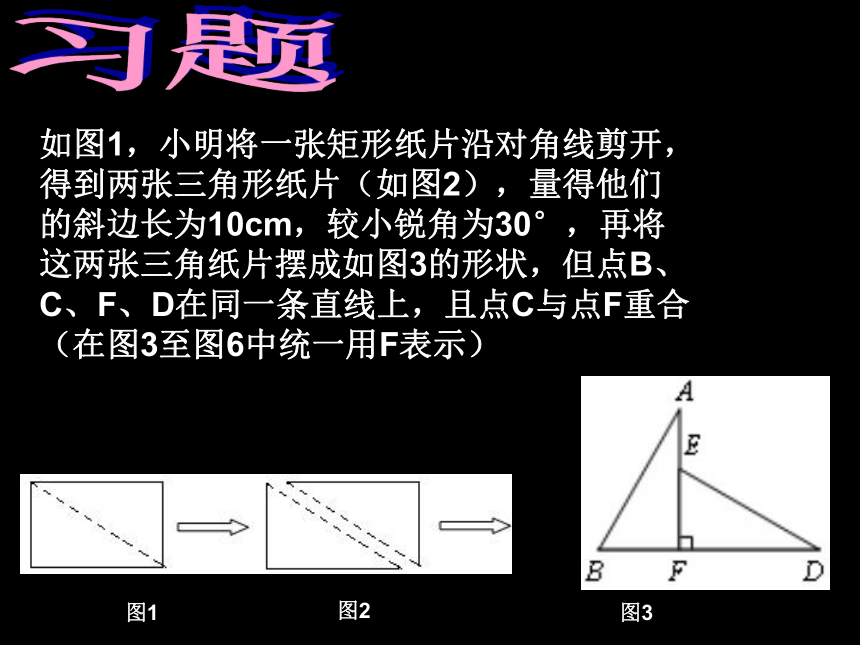
成立吗?简要说明理由。ABDCEF习题如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)图1图3图2习题如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决。
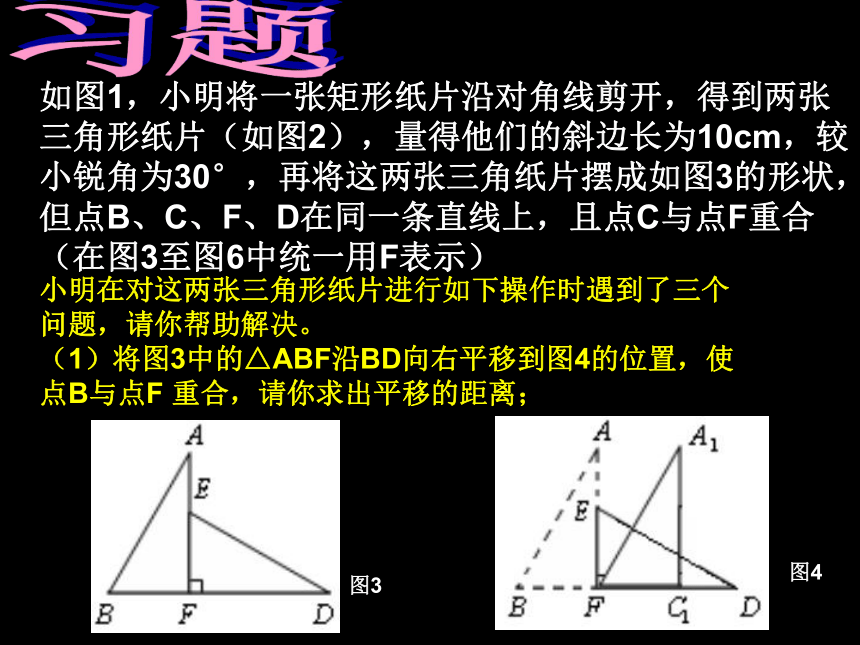
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;图4图3习题如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决。
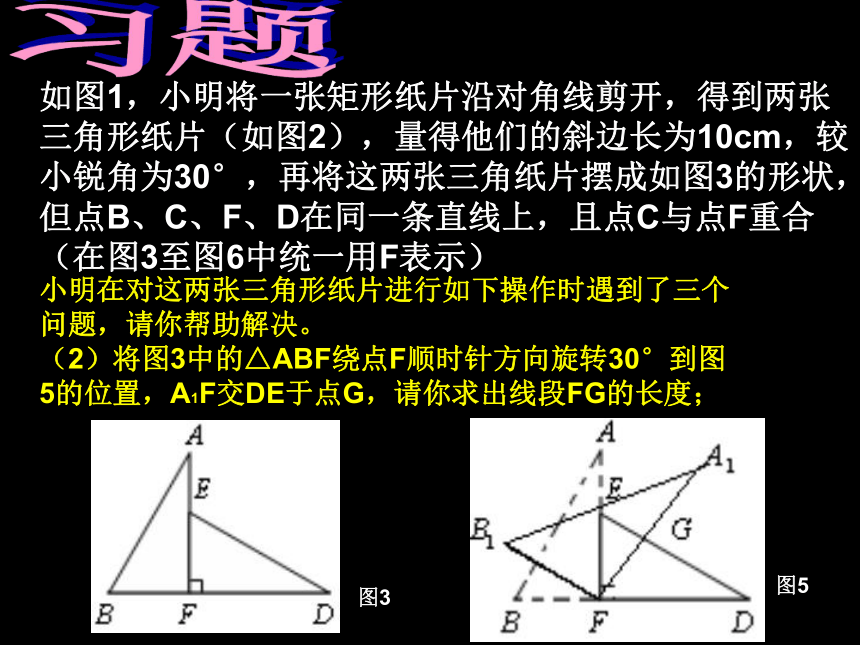
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;图3图5习题如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决。
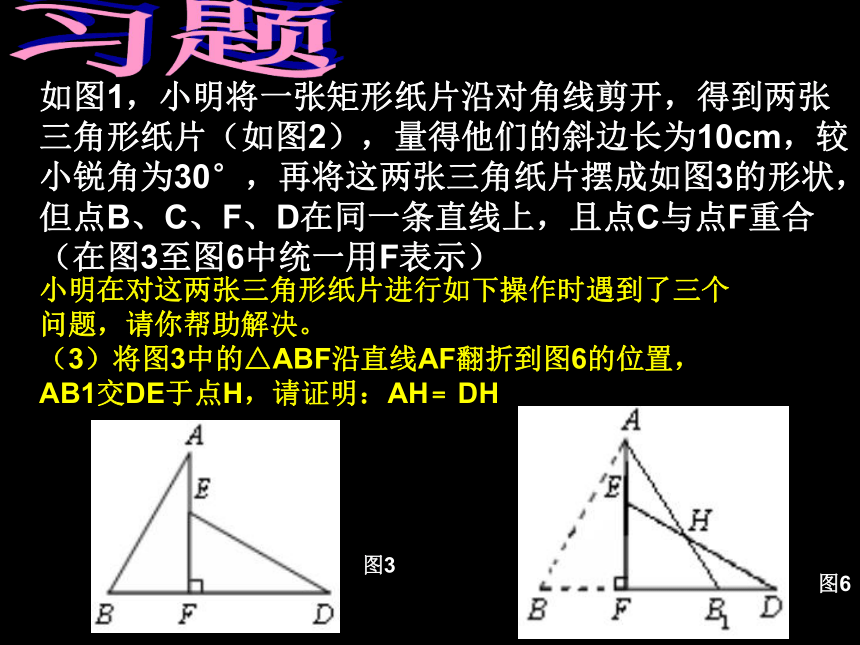
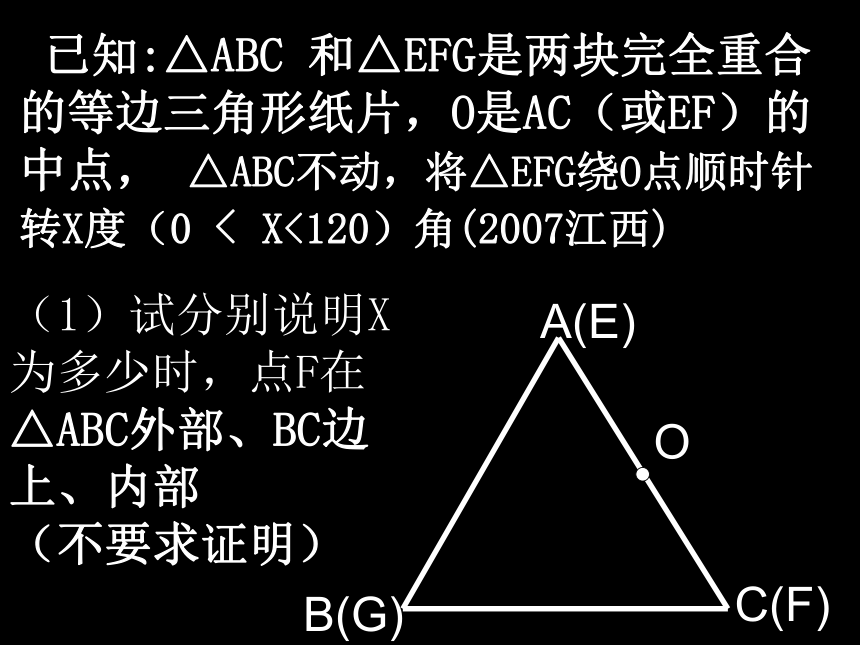
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH﹦DH图6图3(1)操作:固定△ABC,将△C D E绕点C顺时针旋转30? 得到△CDE,联结AD、BE,CE的延长线交AB于F(如图②);′′′′′′ 探究:在图②中,线段BE与AD之间有怎样的大小关系?试证明你的结论.( ′)(1)操作:固定△ABC,将△C D E绕点C顺时针旋转30? 得到△CDE,联结AD、BE,CE的延长线交AB于F(如图②);′′′′′′ 探究:在图②中,线段BE与AD之间有怎样的大小关系?试证明你的结论.ABCDEF图②(30? 已知:△ABC 和△EFG是两块完全重合的等边三角形纸片,O是AC(或EF)的中点, △ABC不动,将△EFG绕O点顺时针转X度(0 < X<120)角(2007江西)(1)试分别说明X
为多少时,点F在
△ABC外部、BC边
上、内部
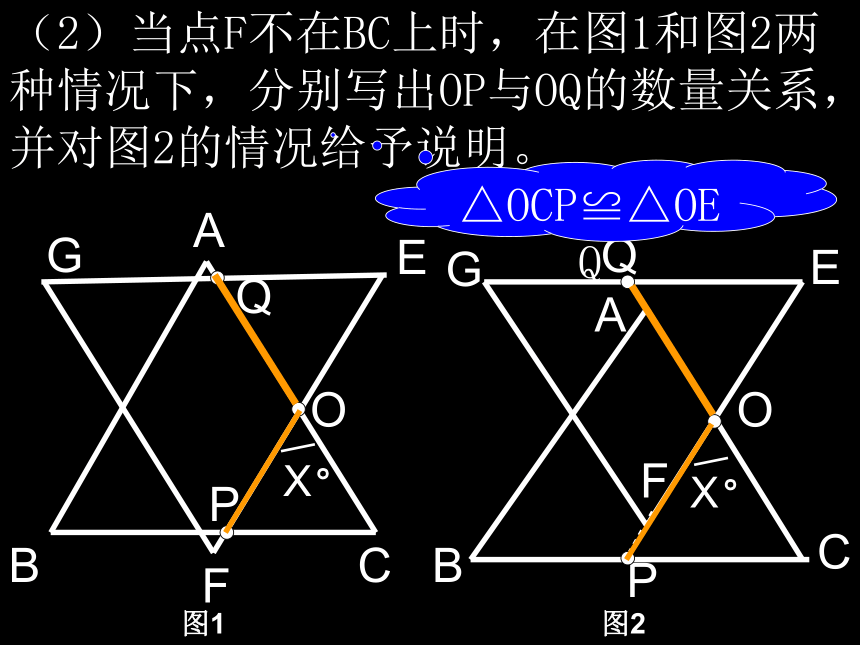
(不要求证明)A(E)B(G)C(F)OABCOABCGEFX。PGEF图1图2Q(2)当点F不在BC上时,在图1和图2两种情况下,分别写出OP与OQ的数量关系,并对图2的情况给予说明。X。PO△OCP≌△OEQQ如图1,已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转。 问题 ⑴在图1中,DE交AB于M,DF交BC于N。①证明DM=DN;②在这一过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边DMBN的面积是否发生变化? 若发生变化,请说明 是如何变化的? 若不发生变化, 求出其面积; 问题第25题图图3图2图1NFEBCDAM⑵继续旋转至如图2的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立, 请给出证明; 若不成立, 请说明理由; 第25题图图2⑶继续旋转至如图3的位置,延长FD交BC于N,延长ED交AB于M,DM=DN是否仍然成立? 若成立, 请给出写出结论, 不用证明。第25题图图3图2四边形背景(07.佳木斯)已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°, ∠ MBN=60°,∠ MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F.
当∠ MBN绕点B旋转到时AE=CF(如图1),易证AE+CF=EF.
当∠ MBN绕点旋转到AE≠CF时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE、CF、EF又有怎样的数量关系?请写出你的猜想,不需证明. 已知正方形ABCD,现将三块不同的
三角板纸片的一个锐角顶点与A重合,适
当绕A点旋转该三角形纸片,该锐角的两
边分别交直线BC、 CD于M、 N,且满足
AN平分 DAM
(1)当M、 N分别
在BC、 CD上时,
求证:
AM=BM+DN
ABMCND且满足AN平分 DAM
(2)当M、 N分别在BC、 CD所在的直线上时,线段AM 、 BM 、DN之间又有怎样的数量关系,请直接写出结论.
ABMCND图2且满足AN平分 DAM
(2)当M、 N分别在BC、 CD所在的直线上时,线段AM 、 BM 、DN之间又有怎样的数量关系,请直接写出结论.
图3ABMCND图3ABMCNDK4xDN=AM+BM5x-1x(07.四川资阳)已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.(1) 求证:BP=DP;
(2) 如图8-2,若四边形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请用反例加以说明;(3) 试选取正方形ABCD的两个顶点,分别与四边形PECF的两个顶点连结,使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论阶梯式习题 四边形 ABCD与四边形CGEF都为正方形,点 D在线段CF上,M 为AE的中点,且CF=2AD.
探 究:线段MD、MF的关系 .MF的关系,并加以证明。 MD=MF
MD⊥MF 阶梯1 四边形 ABCD与四边形CGEF都为正方形,点 D在线段CF上, M 为AE的中点,且CF=2AD.
探究:线段MD、MF的关系 . 究:线段MD、MF的关系, 延长
DM交
FE于N 阶梯1 四边形 ABCD与四边形CGEF都为正方形,点 D在
线段CF上, M 为AE的中点.
探究:线段MD、MF的关系 . 探究:线段MD、MF的关系,并加以证明。 MD=MF
MD⊥MF 阶梯2延长
DM交
FE于N 四边形 ABCD与四边形CGEF都为正方形,点 D在线
段CF上, M 为AE的中点.
探究:线段MD、MF的关系 . 探究:线段MD、MF的 。 阶梯2四边形 ABCD与四边形CGEF为正方形, D在线段CF上, 将正方形CGEF绕点C顺时针旋转45°,DM的延长线交CE于点N,
且AD=NE;其他条件不变; 探究:线段MD、MF的关系 . 连结
FD、
FN
阶梯3 四边形 ABCD与四边形CGEF都为正方形,点 D在线段 CF上, M 为AE的中点.将正方形CGEF绕点C顺时针旋转45°, 其他条件不变;
探究:线段MD、MF的关系 . MD=MF
MD⊥MF 阶梯4 四边形 ABCD与四边形CGEF都为正方形,点 D在线段CF上, M 为AE的中点。 将正方形CGEF绕点C顺时针旋转45°, 其他条件不变;
探究:线段MD、MF的关系 . 延长DM交CE于N,连结 FD、FN .阶梯4方法1 四边形 ABCD与四边形CGEF都为正方形,点 D在线
段CF上, M 为AE的中点. 将正方形CGEF绕点C顺时针旋转45°, 其他条件不变;
探究:线段MD、MF的关系 . 连结AC、FD,延长DM交CE于N,连结 CM并延长交FE于H. 阶梯4方法2 将正方形CGEF绕点C旋转任意角度后,其他条件不变.
探究:线段MD、MF的关系.阶梯5 方法1:延长DM到N,使MN=MD,连结FD、FN、
EN,延长EN与DC延长线交于点H. 方法2:过点E作AD的平行线交DM、DC的延长线于N、H,连结DF、FN.阶梯5 阶梯式习题如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
(1)若把△ADE绕点D旋转一定的角度时,能否与△CDF重合?请说明理由.
(2)现把△DCF向左平移,使DC与AB重合,得△ ABH,AH交ED于点G.
求证:AH⊥ED,
并求AG的长. 与平面直角坐标系如图,点A在Y轴上,点B在X轴上,且OA=OB=1,经过原点O的直线L交线段AB于点C,过C作OC的垂线,与直线X=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:
(1)当△AOC和△BCP全等时,求出t的值。
(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系?并证明你得到的结论。
xyOABC11 在平面直角坐标系中,两个全等的直角三角形的直角顶点及一条直角边重合,点A在第二象限内,点B,点C在轴的负半轴上,
(1)求点C的坐标;
(2)将 绕点C按顺
时针方向旋转30°到
的位置,其中
交直线OA于点E, 分
别交直线OA,CA于点F,G,
则
除外,还有哪几对
全等的三角形,
请直接写出答案;
xyOABC11BAFEG
拼在一起,把含60°角的三角板与这个图形重合,使
三角板的60°角的顶点与点A重合,两边分别与AB、
AC重合。将三角板绕点A按逆时针方向旋转。
(1)当三角板的两边分别与两边BC、CD相交于
点E、F时,如图,通过观察或根据定义你能得
出图中有哪几对三角形全等?并说明理由。
ABECDF将两个全等的等边三角形△ABC和△ACD如图所示
拼在一起,把含60°角的三角板与这个图形重合,使
三角板的60°角的顶点与点A重合,两边分别与AB、
AC重合。将三角板绕点A按逆时针方向旋转。
(2)当三角板两边分别与两边BC、CD的延长线
相交于E、F时,如图,你在①中得出的结论还
成立吗?简要说明理由。ABDCEF习题如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)图1图3图2习题如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决。
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;图4图3习题如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决。
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;图3图5习题如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决。
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH﹦DH图6图3(1)操作:固定△ABC,将△C D E绕点C顺时针旋转30? 得到△CDE,联结AD、BE,CE的延长线交AB于F(如图②);′′′′′′ 探究:在图②中,线段BE与AD之间有怎样的大小关系?试证明你的结论.( ′)(1)操作:固定△ABC,将△C D E绕点C顺时针旋转30? 得到△CDE,联结AD、BE,CE的延长线交AB于F(如图②);′′′′′′ 探究:在图②中,线段BE与AD之间有怎样的大小关系?试证明你的结论.ABCDEF图②(30? 已知:△ABC 和△EFG是两块完全重合的等边三角形纸片,O是AC(或EF)的中点, △ABC不动,将△EFG绕O点顺时针转X度(0 < X<120)角(2007江西)(1)试分别说明X
为多少时,点F在
△ABC外部、BC边
上、内部
(不要求证明)A(E)B(G)C(F)OABCOABCGEFX。PGEF图1图2Q(2)当点F不在BC上时,在图1和图2两种情况下,分别写出OP与OQ的数量关系,并对图2的情况给予说明。X。PO△OCP≌△OEQQ如图1,已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转。 问题 ⑴在图1中,DE交AB于M,DF交BC于N。①证明DM=DN;②在这一过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边DMBN的面积是否发生变化? 若发生变化,请说明 是如何变化的? 若不发生变化, 求出其面积; 问题第25题图图3图2图1NFEBCDAM⑵继续旋转至如图2的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立, 请给出证明; 若不成立, 请说明理由; 第25题图图2⑶继续旋转至如图3的位置,延长FD交BC于N,延长ED交AB于M,DM=DN是否仍然成立? 若成立, 请给出写出结论, 不用证明。第25题图图3图2四边形背景(07.佳木斯)已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°, ∠ MBN=60°,∠ MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F.
当∠ MBN绕点B旋转到时AE=CF(如图1),易证AE+CF=EF.
当∠ MBN绕点旋转到AE≠CF时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE、CF、EF又有怎样的数量关系?请写出你的猜想,不需证明. 已知正方形ABCD,现将三块不同的
三角板纸片的一个锐角顶点与A重合,适
当绕A点旋转该三角形纸片,该锐角的两
边分别交直线BC、 CD于M、 N,且满足
AN平分 DAM
(1)当M、 N分别
在BC、 CD上时,
求证:
AM=BM+DN
ABMCND且满足AN平分 DAM
(2)当M、 N分别在BC、 CD所在的直线上时,线段AM 、 BM 、DN之间又有怎样的数量关系,请直接写出结论.
ABMCND图2且满足AN平分 DAM
(2)当M、 N分别在BC、 CD所在的直线上时,线段AM 、 BM 、DN之间又有怎样的数量关系,请直接写出结论.
图3ABMCND图3ABMCNDK4xDN=AM+BM5x-1x(07.四川资阳)已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.(1) 求证:BP=DP;
(2) 如图8-2,若四边形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请用反例加以说明;(3) 试选取正方形ABCD的两个顶点,分别与四边形PECF的两个顶点连结,使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论阶梯式习题 四边形 ABCD与四边形CGEF都为正方形,点 D在线段CF上,M 为AE的中点,且CF=2AD.
探 究:线段MD、MF的关系 .MF的关系,并加以证明。 MD=MF
MD⊥MF 阶梯1 四边形 ABCD与四边形CGEF都为正方形,点 D在线段CF上, M 为AE的中点,且CF=2AD.
探究:线段MD、MF的关系 . 究:线段MD、MF的关系, 延长
DM交
FE于N 阶梯1 四边形 ABCD与四边形CGEF都为正方形,点 D在
线段CF上, M 为AE的中点.
探究:线段MD、MF的关系 . 探究:线段MD、MF的关系,并加以证明。 MD=MF
MD⊥MF 阶梯2延长
DM交
FE于N 四边形 ABCD与四边形CGEF都为正方形,点 D在线
段CF上, M 为AE的中点.
探究:线段MD、MF的关系 . 探究:线段MD、MF的 。 阶梯2四边形 ABCD与四边形CGEF为正方形, D在线段CF上, 将正方形CGEF绕点C顺时针旋转45°,DM的延长线交CE于点N,
且AD=NE;其他条件不变; 探究:线段MD、MF的关系 . 连结
FD、
FN
阶梯3 四边形 ABCD与四边形CGEF都为正方形,点 D在线段 CF上, M 为AE的中点.将正方形CGEF绕点C顺时针旋转45°, 其他条件不变;
探究:线段MD、MF的关系 . MD=MF
MD⊥MF 阶梯4 四边形 ABCD与四边形CGEF都为正方形,点 D在线段CF上, M 为AE的中点。 将正方形CGEF绕点C顺时针旋转45°, 其他条件不变;
探究:线段MD、MF的关系 . 延长DM交CE于N,连结 FD、FN .阶梯4方法1 四边形 ABCD与四边形CGEF都为正方形,点 D在线
段CF上, M 为AE的中点. 将正方形CGEF绕点C顺时针旋转45°, 其他条件不变;
探究:线段MD、MF的关系 . 连结AC、FD,延长DM交CE于N,连结 CM并延长交FE于H. 阶梯4方法2 将正方形CGEF绕点C旋转任意角度后,其他条件不变.
探究:线段MD、MF的关系.阶梯5 方法1:延长DM到N,使MN=MD,连结FD、FN、
EN,延长EN与DC延长线交于点H. 方法2:过点E作AD的平行线交DM、DC的延长线于N、H,连结DF、FN.阶梯5 阶梯式习题如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
(1)若把△ADE绕点D旋转一定的角度时,能否与△CDF重合?请说明理由.
(2)现把△DCF向左平移,使DC与AB重合,得△ ABH,AH交ED于点G.
求证:AH⊥ED,
并求AG的长. 与平面直角坐标系如图,点A在Y轴上,点B在X轴上,且OA=OB=1,经过原点O的直线L交线段AB于点C,过C作OC的垂线,与直线X=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:
(1)当△AOC和△BCP全等时,求出t的值。
(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系?并证明你得到的结论。
xyOABC11 在平面直角坐标系中,两个全等的直角三角形的直角顶点及一条直角边重合,点A在第二象限内,点B,点C在轴的负半轴上,
(1)求点C的坐标;
(2)将 绕点C按顺
时针方向旋转30°到
的位置,其中
交直线OA于点E, 分
别交直线OA,CA于点F,G,
则
除外,还有哪几对
全等的三角形,
请直接写出答案;
xyOABC11BAFEG
