第三章 图形的平移与旋转复习课件

课件28张PPT。图形的平移与旋转复习学习目标（1分钟）2、会利用性质作图。
3、能够综合运用平移、旋转、轴对称的性质
解决实际问题.
1、巩固平移、旋转、中心对称的相关概念及基本性质； 阅读课本P65-86的内容，思考下列问题：自学指导1（1分钟）学生自学，教师巡视（3分钟）2.平移、旋转 、中心对称各有哪些性质特征？1.平移的两要素是：__________________
旋转的三要素是：_____________________________平移方向和平移距离旋转中心、旋转方向和旋转角度P66P76P823.图形的平移与坐标变化的规律怎样？左右平移，___坐标改变，左____,右____
上下平移，___坐标改变，上____,下____
如果先左（右）平移，再上（下）平移时，横、纵坐标都要改变，此时可以看成是一次平移，平移的方向是__________________
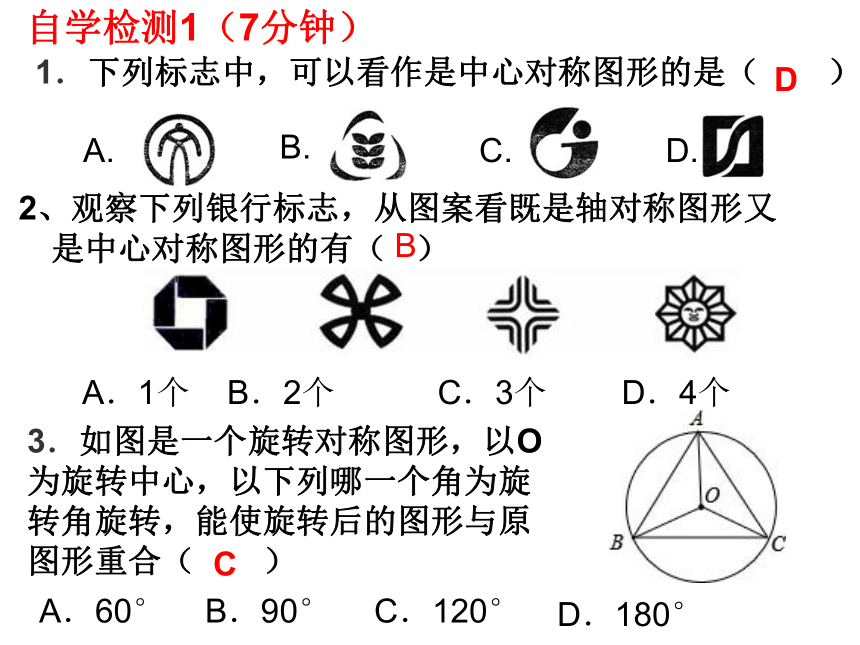
平移的距离是_____________横纵减减加加对应点的连线所在的直线对应点的连线的长度自学检测1（7分钟）1．下列标志中，可以看作是中心对称图形的是（　　）A.B.C.D.D 2、观察下列银行标志，从图案看既是轴对称图形又是中心对称图形的有（ ）

A．1个 B．2个 C．3个 D．4个
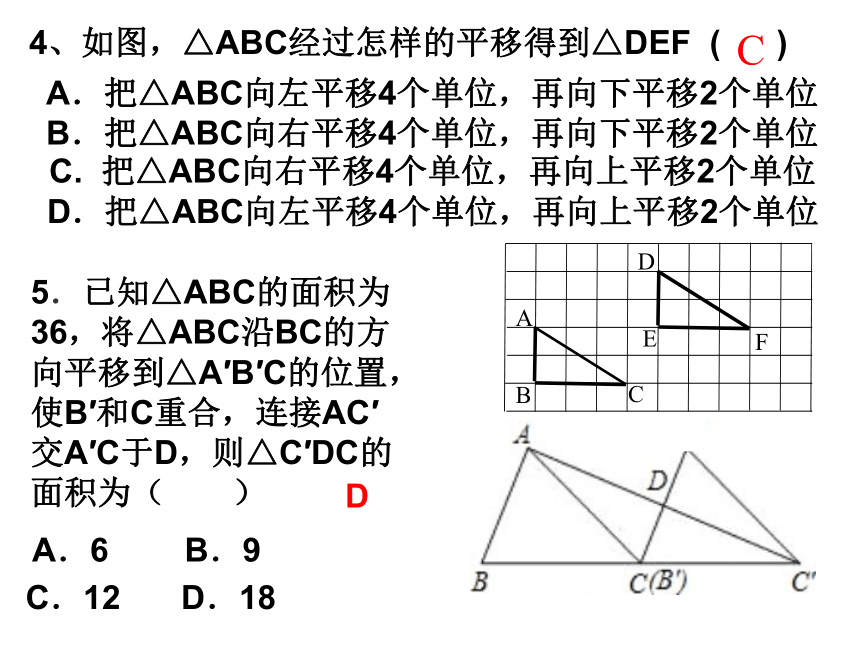
B3．如图是一个旋转对称图形，以O为旋转中心，以下列哪一个角为旋转角旋转，能使旋转后的图形与原图形重合（　　）CD．180° C．120° B．90° A．60° 5．已知△ABC的面积为 36，将△ABC沿BC的方向平移到△A′B′C的位置，使B′和C重合，连接AC′交A′C于D，则△C′DC的面积为（　　） C．12 D．18 B．9 A．6 DA．把△ABC向左平移4个单位，再向下平移2个单位
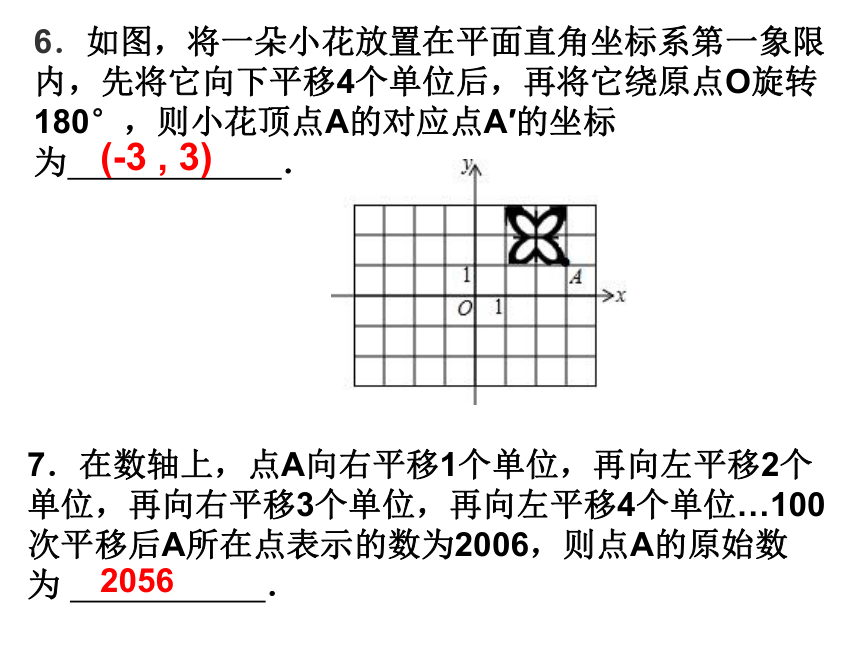
B．把△ABC向右平移4个单位，再向下平移2个单位 C4、如图，△ABC经过怎样的平移得到△DEF ( )C. 把△ABC向右平移4个单位，再向上平移2个单位D．把△ABC向左平移4个单位，再向上平移2个单位 6．如图，将一朵小花放置在平面直角坐标系第一象限内，先将它向下平移4个单位后，再将它绕原点O旋转180°，则小花顶点A的对应点A′的坐标为 ． 7．在数轴上，点A向右平移1个单位，再向左平移2个单位，再向右平移3个单位，再向左平移4个单位…100次平移后A所在点表示的数为2006，则点A的原始数为 ． 2056 (-3 , 3)自学指导2（1分钟）1.看P66例1，P78例题，P82例题，并思考下列问题：
平移、旋转、中心对称的作图方法是什么？
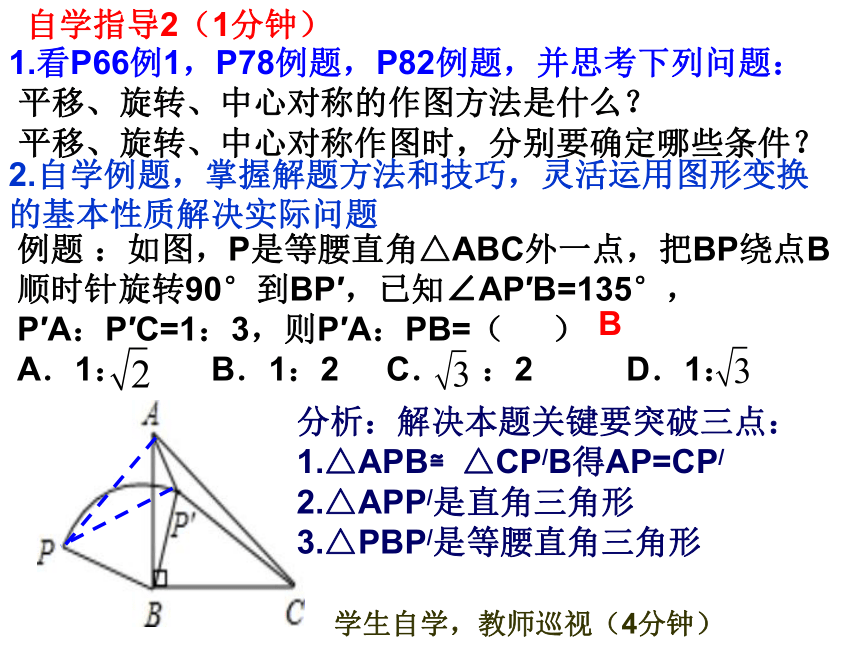
平移、旋转、中心对称作图时，分别要确定哪些条件？2.自学例题，掌握解题方法和技巧，灵活运用图形变换的基本性质解决实际问题例题 ：如图，P是等腰直角△ABC外一点，把BP绕点B顺时针旋转90°到BP′，已知∠AP′B=135°，
P′A：P′C=1：3，则P′A：PB=（ ）
A．1： B．1：2 C． ：2 D．1：B学生自学，教师巡视（4分钟）分析：解决本题关键要突破三点：
1.△APB≌△CP/B得AP=CP/
2.△APP/是直角三角形
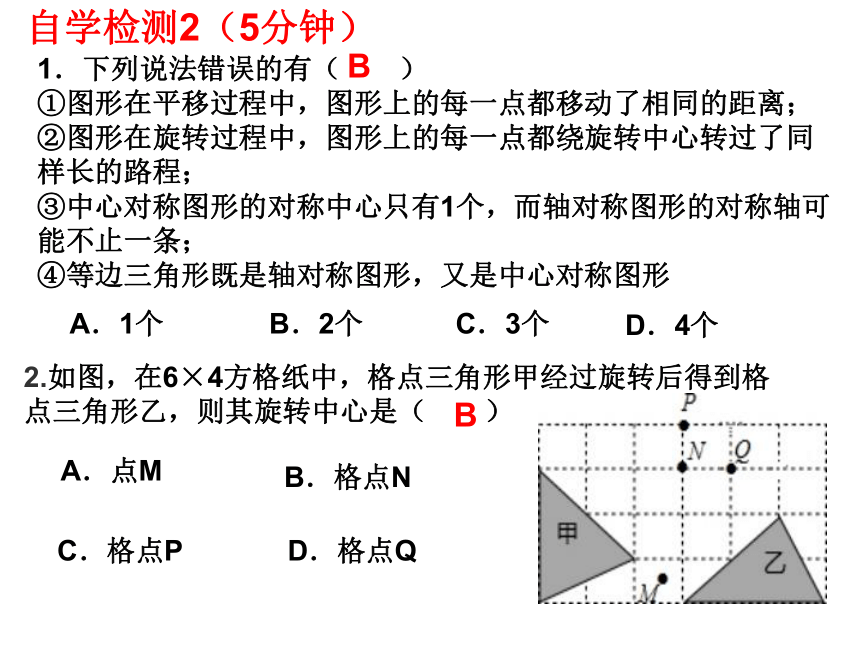
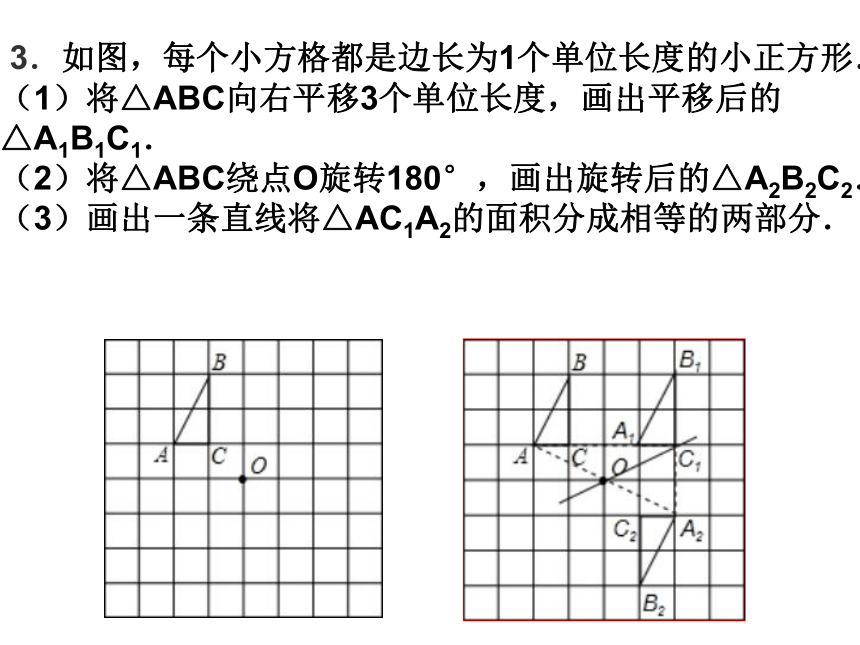
3.△PBP/是等腰直角三角形自学检测2（5分钟）1．下列说法错误的有（　　）①图形在平移过程中，图形上的每一点都移动了相同的距离；②图形在旋转过程中，图形上的每一点都绕旋转中心转过了同样长的路程；③中心对称图形的对称中心只有1个，而轴对称图形的对称轴可能不止一条；④等边三角形既是轴对称图形，又是中心对称图形 A．1个 B．2个 C．3个 D．4个 B 2.如图，在6×4方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是（　　）D．格点Q C．格点P B．格点N A．点M B 3．如图，每个小方格都是边长为1个单位长度的小正方形．（1）将△ABC向右平移3个单位长度，画出平移后的 △A1B1C1．（2）将△ABC绕点O旋转180°，画出旋转后的△A2B2C2．（3）画出一条直线将△AC1A2的面积分成相等的两部分．
5. 如图2所示，在平面内将Rt△ABC绕直角顶点C逆时针旋转90°得到Rt△EFC.若AB=BE的长为 ．,BC=1,则线段 3 4. 如图1，P是正方形ABCD内一点，将△ABP绕点B顺时针方向旋转一定的角度后能与△CBP′重合.若PB=3，则PP′= .图1 P′图2（2013?黄石） 把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=6，DC=7，把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图乙），此时AB与CD1交于点O，则线段AD1的长为（　　） C．4 B．5 B解决此题关键是判断出△ACO是等腰直角三角形.
先求出∠ACD=30°，再根据旋转角求出∠ACD1=45°讨论、更正、点拨（4分钟）点拨：本题用到重要的知识点：1.旋转的性质，2.勾股定理
3.直角三角形中斜边上的中线等于斜边的一半。一、考点：1.平移、旋转、对称的基本性质
2.网格作图
3.基本性质的应用二、难点：1.旋转作图
2.图形的旋转与证明三、易错、易漏点：1.中心对称与中心对称图形的概念
2.旋转作图
3.中心对称与轴对称
4.图形的平移与坐标变化关系
5.旋转具有三要素，缺一不可。课堂小结（3分钟）1．如图的方格纸中，左边图形到右边图形的变换是（　）A．向右平移7格C．绕AB的中点旋转180°，再以AB为对称轴作轴对称
D．以AB为对称轴作轴对称，再向右平移7格
B．以AB的垂直平分线为对称轴作轴对称变换，再以 AB为对称轴作轴对称变换 D 当堂训练（15分钟）2．如图，P是正三角形ABC内的一点，且PA=6，PB=8，PC=10．若将△PAC绕点A逆时针旋转60°后，得到△P′AB，则点P与P′之间的距离为 ，∠APB= ．6150°3．如图，直角三角板ABC的斜边AB=12cm，∠A=30°，将三角板ABC绕C顺时针旋转90°至三角板A'B'C'的位置后，再沿CB方向向左平移，使点B'落在原三角板ABC的斜边AB上，则三角板A'B'C'平移的距离为（　　） B．4cm A．6cm C40 （2）4．如图2所示，△ABC绕点A逆时针旋转某一角度得到△ADE，∠1=∠2=∠3=20°，则旋转角为 度． 若(36,0)5．6.如图，B，C，E是同一直线上的三个点，四边形ABCD与四边形CEFG都是正方形．连接BG，DE．（1）观察猜想BG与DE之间的关系，并证明你的猜想；（2）图中是否存在通过旋转能够互相重合的两个三角形？若存在，请指出，并说出旋转过程；若不存在，请说明理由． 6.解：（1）BG⊥BD，且BG=DE．证明：延长BG与DE交于H点，在△BCG和△DCE中，BC=DC
∠BCG=∠DCE=90°
CG=CE，∴△BCG≌△DCE，∴BG=DE，∠BGC=∠DEC，又∵∠BGC=∠DGH，∠DEC+∠CDE=90°，∴∠DGH+∠GDH=90°，∴∠DHG=90°，故BG⊥DE，且BG=DE．｛（2）存在，△BCG≌△DCE，（1）中已证明，且△BCG和△DCE有共同顶点C，则△DCE沿C点旋转向左90°与△BCG重合． 7．含30°角的直角三角板ABC（∠B=30°）绕直角顶点C沿逆时针方向旋转角α（∠α＜90°），再沿∠A的对边翻折得到△A′B′C，AB与B′C交于点M，A′B′与BC交于点N，A′B′与AB相交于点E．（1）求证：△ACM≌△A′CN；（2）当∠α=30°时，找出ME与MB′的数量关系，并加以说明． 7.（1）证明：∵∠A=∠A′，AC=A′C，∠ACM=∠A'CN=90°-∠MCN，∴△ACM≌△A'CN． （2）解：在Rt△ABC中∵∠B=30°，∴∠A=90°-30°=60°．又∵∠α=30°，∴∠MCN=30°，∴∠ACM=90°-∠MCN=60°．∴∠EMB′=∠AMC=∠A=∠MCA=60°．∵∠B′=∠B=30°，所以三角形MEB′是Rt△MEB′，且∠B′=30°．所以MB′=2ME． 8、如图1．在四边形ABCD中．AB=AD，∠B+∠D=180゜，E、F分别是边BC、CD上的点，且∠BAD=2∠EAF．（1）求证：EF=BE+DF；（2）在（1）问中，若将△AEF绕点A逆时针旋转，当点E、F分别运动到BC、CD延长线上时，如图2所示，试探究EF、BE、DF之间的数量关系． 选做题8.（1)证明：延长CB至M，使BM=DF，连接AM，∵∠ABC+∠D=180°，∠ABC+∠ABM=180°，∴∠D=∠ABM，在△ABM和△ADF中，∴△ABM≌△ADF（SAS），∴AF=AM，∠DAF=∠BAM，∵∠BAD=2∠EAF， BM＝DF∠ABM＝∠D,AB＝AD,∴∠DAF+∠BAE=∠EAF，∴∠EAB+∠BAM=∠EAM=∠EAF，在△FAE和△MAE中，AF＝AM ∠FAE＝∠MAE , AE＝AE , ∴△FAE≌△MAE（SAS），∴EF=EM=BE+BM=BE+DF，即 EF=BE+DF． （2）解：EF、BE、DF之间的关系是EF=BE-DF，理由是：在CB上截取BM=DF，连接AM，∵∠ABC+∠D=180°，∠ADC+∠ADF=180°，∴∠ABC=∠ADF，在△ABM和△ADF中， BM＝DF ,∠B＝∠ADF, AB＝AD ∴△ABM≌△ADF（SAS），∴AF=AM，∠DAF=∠BAM，∵∠BAD=2∠EAF=2（∠EAD+∠DAF）=2（∠EAD+∠BAM）=∠EAF+（∠EAD+∠BAM）?又∵∠BAD=（∠BAM+∠EAD）+∠MAE∴∠MAE=∠EAF在△FAE和△MAE中， AF＝AM ∠FAE＝∠MAE , AE＝AE , ∴△FAE≌△MAE（SAS），∴EF=EM=BE-BM=BE-DF，即EF=BE-DF． 选做题 9（2012?保定一模）如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．（1）求证：△ABQ≌△CAP；（2）当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，则求出它的度数．9. （1）证明：∵△ABC是等边三角形 ∴∠ABQ=∠CAP，AB=CA， 又∵点P、Q运动速度相同， ∴AP=BQ， 在△ABQ与△CAP中，∴△ABQ≌△CAP（SAS）AB＝CA， AP＝BQ ，∠ABQ＝∠CAP （2）解：点P、Q在运动的过程中，∠QMC不变．理由：∵△ABQ≌△CAP，∴∠BAQ=∠ACP，∵∠QMC=∠ACP+∠MAC，∴∠QMC=∠BAQ+∠MAC=∠BAC=60° 选做（3）解：点P、Q在运动到终点后继续在射线AB、BC上运动时，∠QMC不变．理由：∵△ABQ≌△CAP，∴∠BAQ=∠ACP，∵∠QMC=∠BAQ+∠APM，∴∠QMC=∠ACP+∠APM=180°-∠PAC=180°-60°=120°． 10．如图，矩形ABCD中，AB=6，第1次平移将矩形ABCD沿AB的方向向右平移5个单位，得到矩形A1B1C1D1，第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位，得到矩形A2B2C2D2…，第n次平移将矩形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向平移5个单位，得到矩形AnBnCnDn（n＞2）． ???????????????????????????????????????????????????????（1）求AB1和AB2的长．（2）若ABn的长为56，求n． （1）11、16、（2）n=10如图（1）所示，点C为线段AB上一点，△ACM、
△CBN是等边三角形，直线AN、MC交于点E，
直线BM、CN交于点F．（1）求证：AN=MB；（2）将△ACM绕点C按逆时针方向旋转90°，
其他条件不变，在图（2）中补出符合要求的图形，
并判断（1）题中的结论是否依然成立，说明理由． ???????????????????????????????????????????????????????????????????????????????????????????????????
?????????????????????????????????????????????????????????????????????????????????????????????????????????????
11 11（1）证明：∵△ACM、△CBN是等边三角形，∴AC=MC，BC=CN，∠ACM=∠BCN=60°，∴∠ACN=∠MCB=120°，∴△ACN≌△MCB，∴AN=MB． （2）解：连接AN，BM，∵△ACM、△CBN是等边三角形，∴AC=MC，BC=CN，∠ACM=∠BCN=60°，∵∠ACB=90°，∴∠ACN=∠MCB，∴△ACN≌△MCB，∴AN=MB．