6.2 平行四边形的判定(第2课时)同步课件(共24张PPT)
文档属性
| 名称 | 6.2 平行四边形的判定(第2课时)同步课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:47 | ||
图片预览





文档简介
(共24张PPT)
6.2平行四边形的8判定
(第2课时)
1 探索并证明“对角线互相平分的四边形是平行四边形”;
2 应用平行四边形的判定定理解决问题.
判定四边形是平行四边形的方法有哪些?
(1)两组对边分别平行的四边形是平行四边形.
(2)一组对边平行且相等的四边形是平行四边形.
(3)两组对边分别相等的四边形是平行四边形.
核心知识点一:
平行四边形的判定定理3
小明将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD,小明高兴地说:‘’这的确是个平行四边形!”
猜想:对角线互相平分的四边形是平行四边形
你能证明他的猜想吗?
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:
在△AOB和△COD中,
OA=OC (已知),
OB=OD (已知),
∠AOB=∠COD (对顶角相等),
∴△AOB≌△COD(SAS).
∴ ∠BAO=∠OCD ,∠ ABO=∠CDO.
∴AB∥ CD , AD∥ BC.
∴四边形ABCD是平行四边形.
A
C
B
O
D
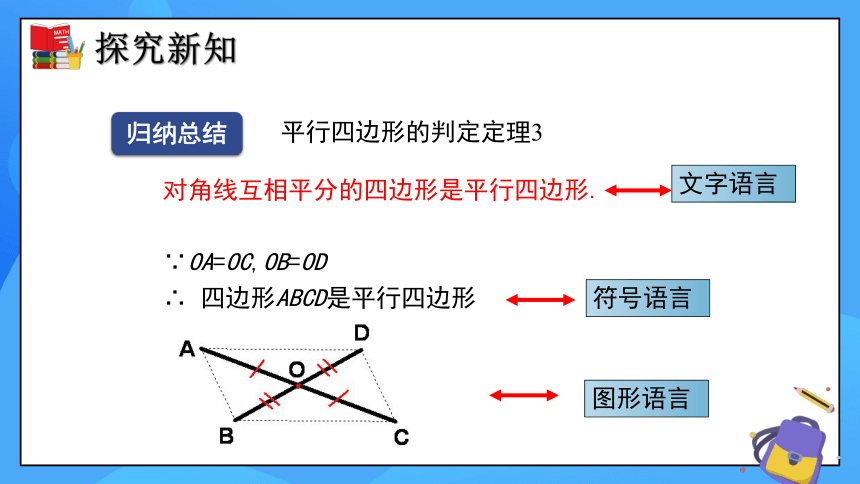
归纳总结
对角线互相平分的四边形是平行四边形.
∵OA=OC,OB=OD
∴ 四边形ABCD是平行四边形
文字语言
符号语言
图形语言
平行四边形的判定定理3
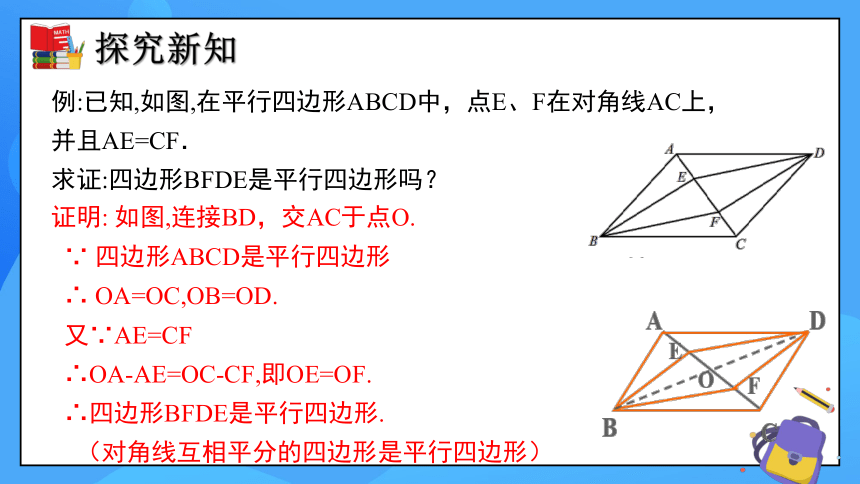
例:已知,如图,在平行四边形ABCD中,点E、F在对角线AC上,并且AE=CF.
求证:四边形BFDE是平行四边形吗?
证明: 如图,连接BD,交AC于点O.
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD.
又∵AE=CF
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE是平行四边形.
(对角线互相平分的四边形是平行四边形)
核心知识点二:
平行四边形的判定定理4
思考:我们可以从角出发来判定一个四边形是否为平行四边形吗?
A
B
C
D
你能根据平行四边形的定义证明它们吗?
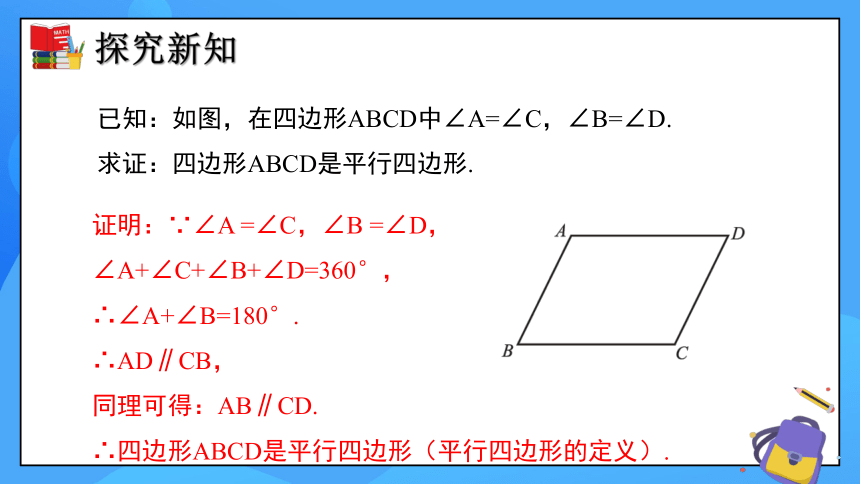
已知:如图,在四边形ABCD中∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
证明:∵∠A =∠C,∠B =∠D,∠A+∠C+∠B+∠D=360°,
∴∠A+∠B=180°.
∴AD∥CB,
同理可得:AB∥CD.
∴四边形ABCD是平行四边形(平行四边形的定义).
平行四边形的判定定理四
A
B
C
D
两组对角分别相等的四边形是平行四边形
∵ ∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形.
归纳总结
文字语言
符号语言
图形语言
从边来判定
1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
1.下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等,②一组对边相等且一条对角线平分另一条对角线,③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分,④对角线互相平分的四边形。
A、①和② B、②和③
C、②和④ D、只有④
D
A
B
C
D
2. 在四边形ABCD中,AC交BD于点O,且AB∥CD,给出以下四种说法:
①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;③如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;其中正确的说法是( )
A.①② B.①③ C.②③ D.②③
C
3.在四边形ABCD中,对角线AC,BD相交于点O,给出下列4组条件:
①AB∥CD,AD∥BC;②AB=CD,AD=BC;
③AO=CO,BO=DO;④AB∥CD,AD=BC.
其中一定能判定这个四边形是平行四边形的条件有( )
A.1组 B.2组 C.3组 D.4组
C
4.如图,四边形ABCD的对角线交于点O,下列条件中不能判定四边形ABCD是平行四边形的是( )
A.OA=OC,OB=OD
B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC
D.AB=CD,AO=CO
D
5.如图,在四边形ABCD中,AC,BD相交于点O.AO=OC,DO=OB,若AB=3,则线段CD的长是( )
C
A.1 B.2 C.3 D.6
6.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,
E、F是对角线AC上的两点,当E,F满足下列哪个条件时,
四边形DEBF不一定是平行四边形. ( )
A OE=OF B.DE=BF
C. ∠ADE= ∠CBF D. ∠ABE= ∠CDF
B
7.在四边形ABCD,对角线AC、BD相交于点O,且OA=OC,OB=OD,∠ABC= 80°,则∠ADC 和∠BCD 的度数分别为( )
A. 80°120 ° B.100° 80°
C. 80° 100° D.120° 80°
C
8.判断下列说法是否正确。
两组对边分别平行的四边形是平行四边形。( )
两组对边分别相等的四边形是平行四边形。( )
一组对边平行,另一组对边相等的四边形是平行四边形。( )
两组对角分别向等的四边形是平行四边形。( )
对角线相等的四边形是平行四边形。( )
√
×
√
√
×
9.已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
∴△ABE≌△FCE(AAS). ∴AE=EF.
又∵BE=CE,∴四边形ABFC是平行四边形.
解:四边形ABFC是平行四边形. 理由如下:
∵AB∥CD,∴∠BAE=∠CFE.
∵E是BC的中点,∴BE=CE.
在△ABE和△FCE中,
10.如图,已知AB∥DE,AB=DE,AF=DC,
求证:四边形BCEF是平行四边形.
证明:连接AE,DB,BE,BE交AD于点O,
∵ABAB平行DE,
∴四边形ABDE是平行四边形,
∴OB=OE,OA=OD.
∵AF=DC,∴OF=OC,
∴四边形BCEF是平行四边形.
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
从对角线考虑
平行四边形的判定方法
两组对角分别相等的四边形是平行四边形(定义拓展)
对角线互相平分的四边形是平行四边形(判定定理3)
“习题6.4”
第1、2、3题
6.2平行四边形的8判定
(第2课时)
1 探索并证明“对角线互相平分的四边形是平行四边形”;
2 应用平行四边形的判定定理解决问题.
判定四边形是平行四边形的方法有哪些?
(1)两组对边分别平行的四边形是平行四边形.
(2)一组对边平行且相等的四边形是平行四边形.
(3)两组对边分别相等的四边形是平行四边形.
核心知识点一:
平行四边形的判定定理3
小明将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD,小明高兴地说:‘’这的确是个平行四边形!”
猜想:对角线互相平分的四边形是平行四边形
你能证明他的猜想吗?
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:
在△AOB和△COD中,
OA=OC (已知),
OB=OD (已知),
∠AOB=∠COD (对顶角相等),
∴△AOB≌△COD(SAS).
∴ ∠BAO=∠OCD ,∠ ABO=∠CDO.
∴AB∥ CD , AD∥ BC.
∴四边形ABCD是平行四边形.
A
C
B
O
D
归纳总结
对角线互相平分的四边形是平行四边形.
∵OA=OC,OB=OD
∴ 四边形ABCD是平行四边形
文字语言
符号语言
图形语言
平行四边形的判定定理3
例:已知,如图,在平行四边形ABCD中,点E、F在对角线AC上,并且AE=CF.
求证:四边形BFDE是平行四边形吗?
证明: 如图,连接BD,交AC于点O.
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD.
又∵AE=CF
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE是平行四边形.
(对角线互相平分的四边形是平行四边形)
核心知识点二:
平行四边形的判定定理4
思考:我们可以从角出发来判定一个四边形是否为平行四边形吗?
A
B
C
D
你能根据平行四边形的定义证明它们吗?
已知:如图,在四边形ABCD中∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
证明:∵∠A =∠C,∠B =∠D,∠A+∠C+∠B+∠D=360°,
∴∠A+∠B=180°.
∴AD∥CB,
同理可得:AB∥CD.
∴四边形ABCD是平行四边形(平行四边形的定义).
平行四边形的判定定理四
A
B
C
D
两组对角分别相等的四边形是平行四边形
∵ ∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形.
归纳总结
文字语言
符号语言
图形语言
从边来判定
1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
1.下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等,②一组对边相等且一条对角线平分另一条对角线,③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分,④对角线互相平分的四边形。
A、①和② B、②和③
C、②和④ D、只有④
D
A
B
C
D
2. 在四边形ABCD中,AC交BD于点O,且AB∥CD,给出以下四种说法:
①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;③如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;其中正确的说法是( )
A.①② B.①③ C.②③ D.②③
C
3.在四边形ABCD中,对角线AC,BD相交于点O,给出下列4组条件:
①AB∥CD,AD∥BC;②AB=CD,AD=BC;
③AO=CO,BO=DO;④AB∥CD,AD=BC.
其中一定能判定这个四边形是平行四边形的条件有( )
A.1组 B.2组 C.3组 D.4组
C
4.如图,四边形ABCD的对角线交于点O,下列条件中不能判定四边形ABCD是平行四边形的是( )
A.OA=OC,OB=OD
B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC
D.AB=CD,AO=CO
D
5.如图,在四边形ABCD中,AC,BD相交于点O.AO=OC,DO=OB,若AB=3,则线段CD的长是( )
C
A.1 B.2 C.3 D.6
6.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,
E、F是对角线AC上的两点,当E,F满足下列哪个条件时,
四边形DEBF不一定是平行四边形. ( )
A OE=OF B.DE=BF
C. ∠ADE= ∠CBF D. ∠ABE= ∠CDF
B
7.在四边形ABCD,对角线AC、BD相交于点O,且OA=OC,OB=OD,∠ABC= 80°,则∠ADC 和∠BCD 的度数分别为( )
A. 80°120 ° B.100° 80°
C. 80° 100° D.120° 80°
C
8.判断下列说法是否正确。
两组对边分别平行的四边形是平行四边形。( )
两组对边分别相等的四边形是平行四边形。( )
一组对边平行,另一组对边相等的四边形是平行四边形。( )
两组对角分别向等的四边形是平行四边形。( )
对角线相等的四边形是平行四边形。( )
√
×
√
√
×
9.已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
∴△ABE≌△FCE(AAS). ∴AE=EF.
又∵BE=CE,∴四边形ABFC是平行四边形.
解:四边形ABFC是平行四边形. 理由如下:
∵AB∥CD,∴∠BAE=∠CFE.
∵E是BC的中点,∴BE=CE.
在△ABE和△FCE中,
10.如图,已知AB∥DE,AB=DE,AF=DC,
求证:四边形BCEF是平行四边形.
证明:连接AE,DB,BE,BE交AD于点O,
∵ABAB平行DE,
∴四边形ABDE是平行四边形,
∴OB=OE,OA=OD.
∵AF=DC,∴OF=OC,
∴四边形BCEF是平行四边形.
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
从对角线考虑
平行四边形的判定方法
两组对角分别相等的四边形是平行四边形(定义拓展)
对角线互相平分的四边形是平行四边形(判定定理3)
“习题6.4”
第1、2、3题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
