锐角三角函数-余弦与正切
文档属性
| 名称 | 锐角三角函数-余弦与正切 |

|
|
| 格式 | zip | ||
| 文件大小 | 292.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-28 00:00:00 | ||
图片预览

文档简介
“一·三·六”导学案——九年级数学(下)
编号:2802 班级: 姓名:
课题:锐角三角函数
主备: 审核: 时间:年 月 日
【明确目标】
1.掌握和理解余弦、正切函数的概念,能够运用cosA、tanA表示直角三角形两边的比.
2.进一步体会锐角三角函数的定义,从而掌握锐角三种三角函数的变化规律.
3.深刻体会数学知识来源于实际生活又服务于实际生活.
【自主预习】
1.什么是正弦?如何求一个角的正弦值?
2.在直角三角形中,当锐角么A的度数一定时,它的邻边比斜边、对边比邻边是否也是一个固定值?
3.把锐角A的__________边与斜边的比叫做∠A的余弦,记作__________,即cosA=__________.【来源:21·世纪·教育·网】
4.把锐角A的__________边与__________边的比叫做∠A的正切,记作__________,即tanA=__________.21·世纪*教育网
5.锐角AR的正弦,__________,__________都是∠A的锐角三角函数.
6.如图,已知在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosB的值为__________.www-2-1-cnjy-com
7.在Rt△ABC中,若∠C=90°,a=6,b=8,则tanA=__________.
8.在Rt△ABC中,∠C=90°,a=8,c=17,∠A的三个三角函数值分别是____________________________.2-1-c-n-j-y
【合作探究】
活动1 新知探究:余弦、正切
(1)学生自主学习教材P64~67中的探究.
(2)学生小组代表讲述对余弦、正切的理解.
(3)研讨cosA,tanA的取值范围.
(4)新知应用
①学生完成P65页例2.
②教材P65练习第1、2题.
活动2 三角函数
学生交流对三角函数的理解:
(1)锐角的三角函数是两条边的比值.
(2)在直角三角形中,对于锐角A的每一个确定的值,sinA、cosA、tanA都有唯一的值与它对应,故把sinA、cosA、tanA叫做∠A的三角函数.
活动3 新知(综合)应用
小组讨论(合作交流)
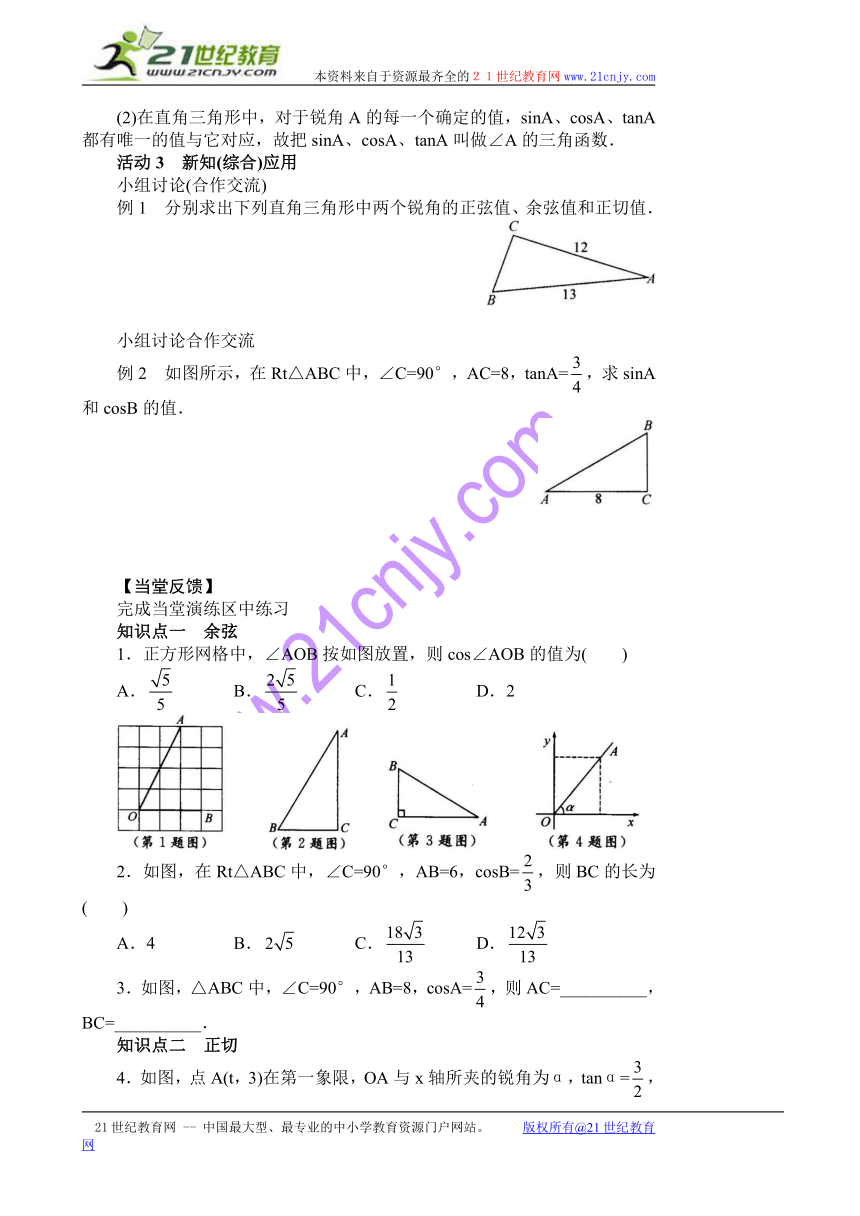
例1 分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
小组讨论合作交流
例2 如图所示,在Rt△ABC中,∠C=90°,AC=8,tanA=,求sinA和cosB的值.21cnjy.com
【当堂反馈】
完成当堂演练区中练习
知识点一 余弦
1.正方形网格中,∠AOB按如图放置,则cos∠AOB的值为( )
A. B. C. D.2
2.如图,在Rt△ABC中,∠C=90°,AB=6,cosB=,则BC的长为( )
A.4 B. C. D.
3.如图,△ABC中,∠C=90°,AB=8,cosA=,则AC=__________,BC=__________.21世纪教育网版权所有
知识点二 正切
4.如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是( )
A.1 B.1.5 C.2 D.3
5.在△ABC中,∠C=90°,AB=3AC,则tanA=( )
A. B.3 C. D.
6.如图,将矩形ABCD沿CE折叠,点B恰好落在边AD的F处,如果,那么tan∠DCF的值是__________.
知识点三 锐角三角函数
7.在△ABC中,∠C=90°,AB=25,BC=24.
(1)求AC的长;
(2)求∠A的三个锐角三角函数值.
【拓展提升】
1.如图所示,△ABC中,∠C=90°,∠BAC的平分线交BC于D,则=__________.
2.如图所示,△ABC中,∠C=90°,D是BC上一点,AC=2,CD=1,记∠CAD=α.
①试写出α的三个三角函数值;
②若∠B=α,求BD的长.
【课后检测】
一、选择题
1.如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OP与x轴正半轴的夹角α的正切值是,则sinα的值为( )
A. B. C. D.
第1题图 第2题图
2.直角三角形纸片的两条直角边长分别为6和8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则cos∠CBE的值是( )
A. B. C. D.
二、填空题
3.如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF,如图2,展开再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为M,EM交AB于N,则tan∠ANE=__________.21教育网
第3题图 第4题图
4.如图,在直角坐标系中,四边形OABC是直角梯形,BC∥OA,⊙P分别与OA、OC、BC相切于点E、D、B,与AB交于点F.已知A(2,0),B(1,2),则tan∠FDE=__________.www.21-cn-jy.com
三、解答题
5.如图所示,在Rt△ABC中,∠C=90°,已知sinA=.
(1)求cosA,tanA的值;
(2)若BC=3,试求AB,AC的长.
6.如图,在直角坐标系中,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.21·cn·jy·com
(1)求点B的坐标;
(2)求cos∠BAO的值.
7.如图,在△ABC中,∠C=90°,点D、E分别在AC、AB上,BD平分∠ABC,DE⊥AB,AE=6,cosA=.求:2·1·c·n·j·y
(1)DE、CD的长;
(2)tan∠DBC的值.
编号:2802 班级: 姓名:
课题:锐角三角函数
主备: 审核: 时间:年 月 日
【明确目标】
1.掌握和理解余弦、正切函数的概念,能够运用cosA、tanA表示直角三角形两边的比.
2.进一步体会锐角三角函数的定义,从而掌握锐角三种三角函数的变化规律.
3.深刻体会数学知识来源于实际生活又服务于实际生活.
【自主预习】
1.什么是正弦?如何求一个角的正弦值?
2.在直角三角形中,当锐角么A的度数一定时,它的邻边比斜边、对边比邻边是否也是一个固定值?
3.把锐角A的__________边与斜边的比叫做∠A的余弦,记作__________,即cosA=__________.【来源:21·世纪·教育·网】
4.把锐角A的__________边与__________边的比叫做∠A的正切,记作__________,即tanA=__________.21·世纪*教育网
5.锐角AR的正弦,__________,__________都是∠A的锐角三角函数.
6.如图,已知在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosB的值为__________.www-2-1-cnjy-com
7.在Rt△ABC中,若∠C=90°,a=6,b=8,则tanA=__________.
8.在Rt△ABC中,∠C=90°,a=8,c=17,∠A的三个三角函数值分别是____________________________.2-1-c-n-j-y
【合作探究】
活动1 新知探究:余弦、正切
(1)学生自主学习教材P64~67中的探究.
(2)学生小组代表讲述对余弦、正切的理解.
(3)研讨cosA,tanA的取值范围.
(4)新知应用
①学生完成P65页例2.
②教材P65练习第1、2题.
活动2 三角函数
学生交流对三角函数的理解:
(1)锐角的三角函数是两条边的比值.
(2)在直角三角形中,对于锐角A的每一个确定的值,sinA、cosA、tanA都有唯一的值与它对应,故把sinA、cosA、tanA叫做∠A的三角函数.
活动3 新知(综合)应用
小组讨论(合作交流)
例1 分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
小组讨论合作交流
例2 如图所示,在Rt△ABC中,∠C=90°,AC=8,tanA=,求sinA和cosB的值.21cnjy.com
【当堂反馈】
完成当堂演练区中练习
知识点一 余弦
1.正方形网格中,∠AOB按如图放置,则cos∠AOB的值为( )
A. B. C. D.2
2.如图,在Rt△ABC中,∠C=90°,AB=6,cosB=,则BC的长为( )
A.4 B. C. D.
3.如图,△ABC中,∠C=90°,AB=8,cosA=,则AC=__________,BC=__________.21世纪教育网版权所有
知识点二 正切
4.如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是( )
A.1 B.1.5 C.2 D.3
5.在△ABC中,∠C=90°,AB=3AC,则tanA=( )
A. B.3 C. D.
6.如图,将矩形ABCD沿CE折叠,点B恰好落在边AD的F处,如果,那么tan∠DCF的值是__________.
知识点三 锐角三角函数
7.在△ABC中,∠C=90°,AB=25,BC=24.
(1)求AC的长;
(2)求∠A的三个锐角三角函数值.
【拓展提升】
1.如图所示,△ABC中,∠C=90°,∠BAC的平分线交BC于D,则=__________.
2.如图所示,△ABC中,∠C=90°,D是BC上一点,AC=2,CD=1,记∠CAD=α.
①试写出α的三个三角函数值;
②若∠B=α,求BD的长.
【课后检测】
一、选择题
1.如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OP与x轴正半轴的夹角α的正切值是,则sinα的值为( )
A. B. C. D.
第1题图 第2题图
2.直角三角形纸片的两条直角边长分别为6和8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则cos∠CBE的值是( )
A. B. C. D.
二、填空题
3.如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF,如图2,展开再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为M,EM交AB于N,则tan∠ANE=__________.21教育网
第3题图 第4题图
4.如图,在直角坐标系中,四边形OABC是直角梯形,BC∥OA,⊙P分别与OA、OC、BC相切于点E、D、B,与AB交于点F.已知A(2,0),B(1,2),则tan∠FDE=__________.www.21-cn-jy.com
三、解答题
5.如图所示,在Rt△ABC中,∠C=90°,已知sinA=.
(1)求cosA,tanA的值;
(2)若BC=3,试求AB,AC的长.
6.如图,在直角坐标系中,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.21·cn·jy·com
(1)求点B的坐标;
(2)求cos∠BAO的值.
7.如图,在△ABC中,∠C=90°,点D、E分别在AC、AB上,BD平分∠ABC,DE⊥AB,AE=6,cosA=.求:2·1·c·n·j·y
(1)DE、CD的长;
(2)tan∠DBC的值.
