锐角三角函数--特殊角的三角函数值
文档属性
| 名称 | 锐角三角函数--特殊角的三角函数值 | 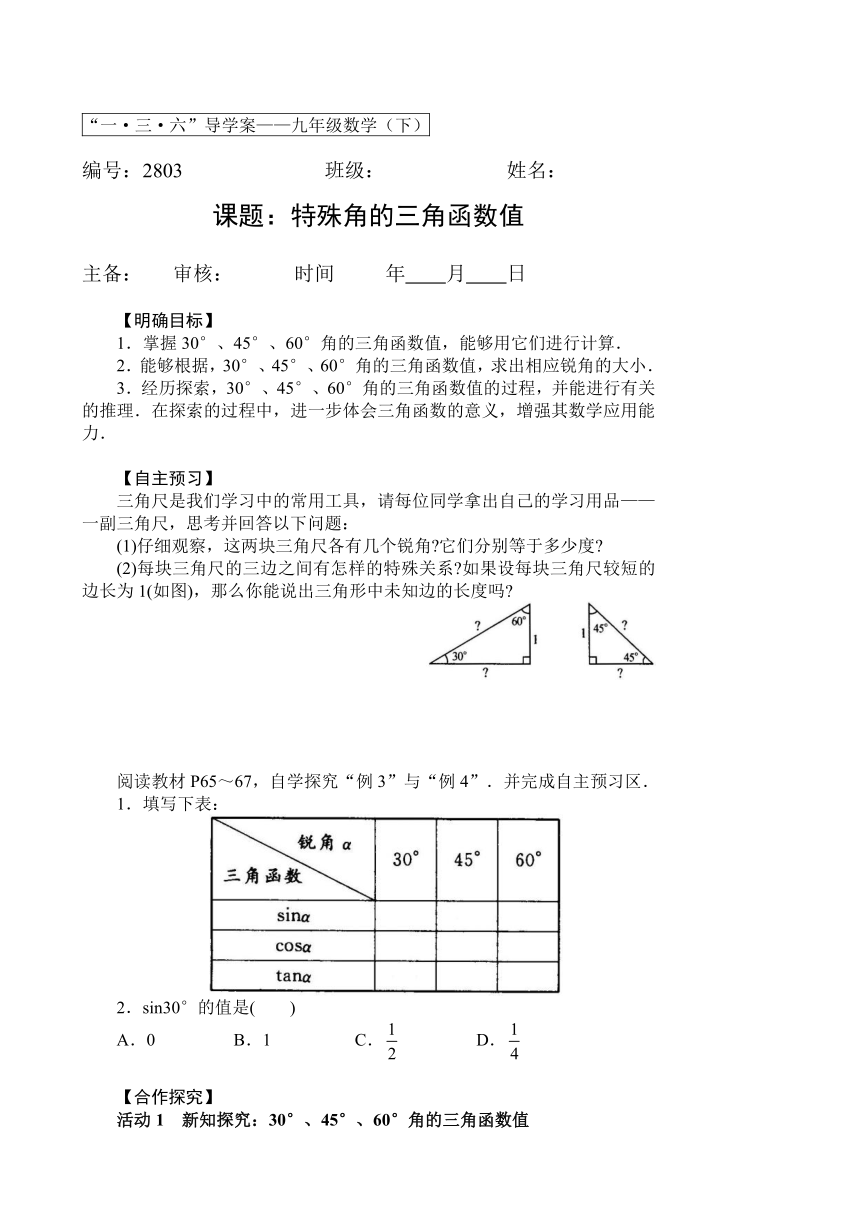 | |
| 格式 | zip | ||
| 文件大小 | 315.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-28 22:35:07 | ||
图片预览


文档简介
“一·三·六”导学案——九年级数学(下)
编号:2803 班级: 姓名:
课题:特殊角的三角函数值
主备: 审核: 时间 年 月 日
【明确目标】
1.掌握30°、45°、60°角的三角函数值,能够用它们进行计算.
2.能够根据,30°、45°、60°角的三角函数值,求出相应锐角的大小.
3.经历探索,30°、45°、60°角的三角函数值的过程,并能进行有关的推理.在探索的过程中,进一步体会三角函数的意义,增强其数学应用能力.
【自主预习】
三角尺是我们学习中的常用工具,请每位同学拿出自己的学习用品——一副三角尺,思考并回答以下问题:
(1)仔细观察,这两块三角尺各有几个锐角?它们分别等于多少度?
(2)每块三角尺的三边之间有怎样的特殊关系?如果设每块三角尺较短的边长为1(如图),那么你能说出三角形中未知边的长度吗?
阅读教材P65~67,自学探究“例3”与“例4”.并完成自主预习区.
1.填写下表:
2.sin30°的值是( )
A.0 B.1 C. D.
【合作探究】
活动1 新知探究:30°、45°、60°角的三角函数值
(1)在30°、45°、60°、90°角的三角形中,分别求出30°、45°、60°角的三角函数值.
(2)建立表格,发现规律,便于记忆,同时讨论一下三角函数的增减性.
活动2 新知应用
学生独立学习教材P66—67例3、例4.
小组讨论(1)
例1 求下列各式的值;
①cos230°+sin230°;
②.
例2 如图所示,在高为2m,斜坡面与地平面夹角为α的楼梯表面铺地毯,楼梯宽2m,共需地毯的面积为m2,则α为多少度?
【当堂反馈】
教材P67练习第1、2题.
知识点一 特殊角的三角函数值的计算
1.计算cos30°=( )
A. B. C. D.
2.3tan30°的值等于( )
A. B. C. D.
3.计算:sin260°+cos60°-tan45°=__________.
4.计算:
(1)sin45°+cos60°; (2)cos30°·tan60°-tan45°;
(3)sin230°+cos230°; (4)·sin45°+sin30°·cos60°.
知识点二 由三角函数值求特殊角
5.若∠A是锐角,tanA=,则∠A=__________;若cosα-=0,则锐角α的度数为__________.
6.已知∠B为锐角,且1-2sinB=0,则cosB等于( )
A. B. C.或 D.1
7.如果△ABC中,sinA=cosB=,则下列最确切的结论是( )
A.△ABC是直角三角形 B.△ABC是等腰三角形
C.△ABC是等腰直角三角形 D.△ABC是锐角三角形
【拓展提升】
1.若4cos2α-(2+2)cosα+=0,则锐角α=__________.
2.化简=__________.
3.思考怎样解决15°、75°、105°等角三角函数值的相关问题.
4.阅读下面的材料,先完成阅读填空,再按要求答题.
观察上述等式,猜想:对任意锐角A,都有sin2A+cos2A=______.④
(1)如图,在锐角三角形ABC中,利用三角函数的定义及勾股定理证明你的猜想;
(2)已知:∠A为锐角(cosA>o)且sinA=,求cosA.
【课后检测】
一、选择题
1.下列计算错误的是( )
A.sin60°-sin30°-sin30° B.sin245°+cos245°=1
C.tan60°= D.sin30°-cos60°
2.式子2cos30°-tan45°-的值是( )
A.-2 B.0 C. D.2
3.在△ABC中,若|sinA-|+(cosB-)2=0,则∠C的度数是( )
A.30° B.45° C.60° D.90°
二、填空题
4.在△ABC中,若∠A、∠B满足|cosA-|+(sinB-)2=0,则∠C=__________.
5.若a=3-tan60°,则(1-)÷=__________.
三、解答题
6.计算:
7.已知:如图,△ABC中,CD⊥AB于D,AD=CD,tanB=,试求∠ACB的度数.
编号:2803 班级: 姓名:
课题:特殊角的三角函数值
主备: 审核: 时间 年 月 日
【明确目标】
1.掌握30°、45°、60°角的三角函数值,能够用它们进行计算.
2.能够根据,30°、45°、60°角的三角函数值,求出相应锐角的大小.
3.经历探索,30°、45°、60°角的三角函数值的过程,并能进行有关的推理.在探索的过程中,进一步体会三角函数的意义,增强其数学应用能力.
【自主预习】
三角尺是我们学习中的常用工具,请每位同学拿出自己的学习用品——一副三角尺,思考并回答以下问题:
(1)仔细观察,这两块三角尺各有几个锐角?它们分别等于多少度?
(2)每块三角尺的三边之间有怎样的特殊关系?如果设每块三角尺较短的边长为1(如图),那么你能说出三角形中未知边的长度吗?
阅读教材P65~67,自学探究“例3”与“例4”.并完成自主预习区.
1.填写下表:
2.sin30°的值是( )
A.0 B.1 C. D.
【合作探究】
活动1 新知探究:30°、45°、60°角的三角函数值
(1)在30°、45°、60°、90°角的三角形中,分别求出30°、45°、60°角的三角函数值.
(2)建立表格,发现规律,便于记忆,同时讨论一下三角函数的增减性.
活动2 新知应用
学生独立学习教材P66—67例3、例4.
小组讨论(1)
例1 求下列各式的值;
①cos230°+sin230°;
②.
例2 如图所示,在高为2m,斜坡面与地平面夹角为α的楼梯表面铺地毯,楼梯宽2m,共需地毯的面积为m2,则α为多少度?
【当堂反馈】
教材P67练习第1、2题.
知识点一 特殊角的三角函数值的计算
1.计算cos30°=( )
A. B. C. D.
2.3tan30°的值等于( )
A. B. C. D.
3.计算:sin260°+cos60°-tan45°=__________.
4.计算:
(1)sin45°+cos60°; (2)cos30°·tan60°-tan45°;
(3)sin230°+cos230°; (4)·sin45°+sin30°·cos60°.
知识点二 由三角函数值求特殊角
5.若∠A是锐角,tanA=,则∠A=__________;若cosα-=0,则锐角α的度数为__________.
6.已知∠B为锐角,且1-2sinB=0,则cosB等于( )
A. B. C.或 D.1
7.如果△ABC中,sinA=cosB=,则下列最确切的结论是( )
A.△ABC是直角三角形 B.△ABC是等腰三角形
C.△ABC是等腰直角三角形 D.△ABC是锐角三角形
【拓展提升】
1.若4cos2α-(2+2)cosα+=0,则锐角α=__________.
2.化简=__________.
3.思考怎样解决15°、75°、105°等角三角函数值的相关问题.
4.阅读下面的材料,先完成阅读填空,再按要求答题.
观察上述等式,猜想:对任意锐角A,都有sin2A+cos2A=______.④
(1)如图,在锐角三角形ABC中,利用三角函数的定义及勾股定理证明你的猜想;
(2)已知:∠A为锐角(cosA>o)且sinA=,求cosA.
【课后检测】
一、选择题
1.下列计算错误的是( )
A.sin60°-sin30°-sin30° B.sin245°+cos245°=1
C.tan60°= D.sin30°-cos60°
2.式子2cos30°-tan45°-的值是( )
A.-2 B.0 C. D.2
3.在△ABC中,若|sinA-|+(cosB-)2=0,则∠C的度数是( )
A.30° B.45° C.60° D.90°
二、填空题
4.在△ABC中,若∠A、∠B满足|cosA-|+(sinB-)2=0,则∠C=__________.
5.若a=3-tan60°,则(1-)÷=__________.
三、解答题
6.计算:
7.已知:如图,△ABC中,CD⊥AB于D,AD=CD,tanB=,试求∠ACB的度数.
