概率的基本性质
图片预览




文档简介
课件15张PPT。概率的基本性质事件
的关系
和运算 概率的
几个基
本性质 一、 事件的关系和运算1.包含关系
2.相等关系
3.事件的并 (或和)
4.事件的交 (或积)
5.事件的互斥
6.对立事件
事件的运算事件的关系1、投掷一枚硬币,考察正面还是反面朝上.
A={正面朝上} ,B={反面朝上} A,B是对立事件 A,B是互斥(事件) 2、某人对靶射击一次,观察命中环数
A =“命中偶数环” B =“命中奇数环”
C =“命中 o 数环”A,B是互斥事件A,B是对立事件3、一名学生独立解答两道物理习题,考察这两道
习题的解答情况.
记 A = “该学生会解答第一题,不会解答第二题”
B = “该学生会解答第一题,还会解答第二题”
试回答:
1. 事件A 与事件B 互斥吗?为什么?
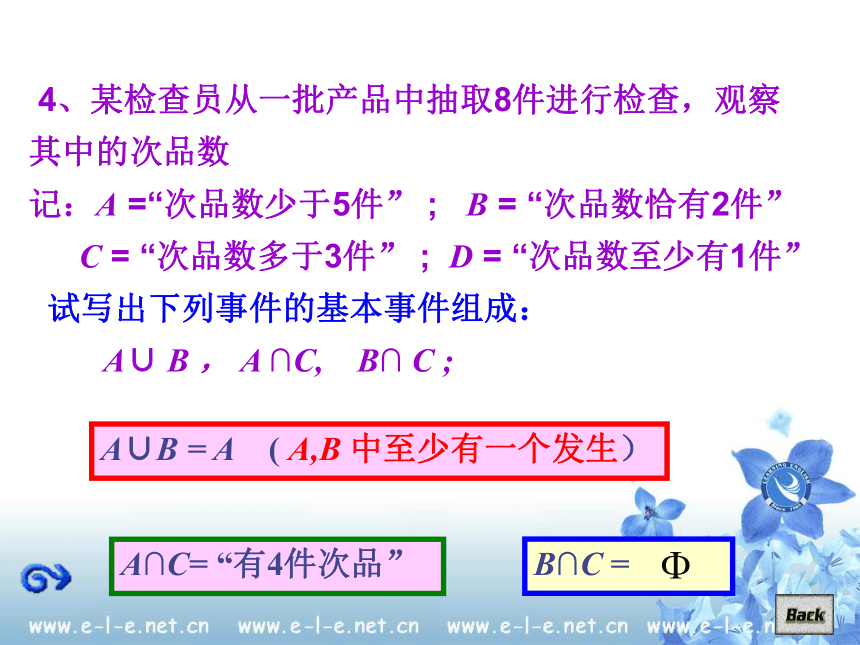
2. 事件A 与事件B 互为对立事件吗?为什么? 4、某检查员从一批产品中抽取8件进行检查,观察其中的次品数
记:A =“次品数少于5件” ; B = “次品数恰有2件”
C = “次品数多于3件” ; D = “次品数至少有1件”
试写出下列事件的基本事件组成:
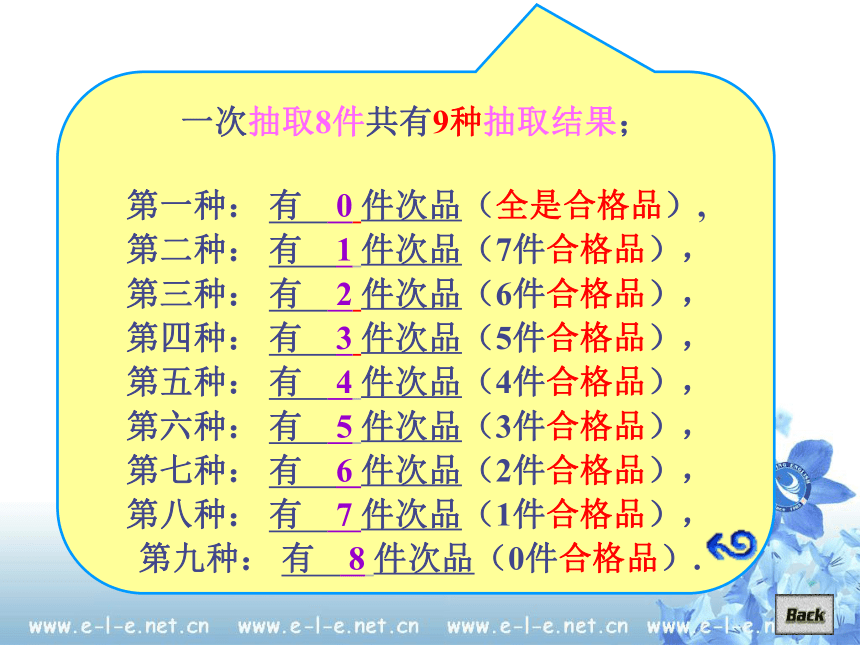
A∪ B , A ∩C, B∩ C ;A∪B = A ( A,B 中至少有一个发生)A∩C= “有4件次品”一次抽取8件共有9种抽取结果;
第一种: 有 0 件次品(全是合格品),
第二种: 有 1 件次品(7件合格品),
第三种: 有 2 件次品(6件合格品),
第四种: 有 3 件次品(5件合格品),
第五种: 有 4 件次品(4件合格品),
第六种: 有 5 件次品(3件合格品),
第七种: 有 6 件次品(2件合格品),
第八种: 有 7 件次品(1件合格品),
第九种: 有 8 件次品(0件合格品).3.1.3 概率的基本性质二、概率的几个基本性质(1)、对于任何事件的概率的范围是:
0≤P(A)≤1
其中不可能事件的概率是P(A)=0
必然事件的概率是P(A)=1
不可能事件与必然事件是一般事件的特殊情况(2)、当事件A与事件B互斥时,A∪B的频率
fn(A∪B)= fn(A)+ fn(B)
由此得到概率的加法公式:
如果事件A与事件B互斥,则
P(A∪B)=P(A)+P(B)3.1.3 概率的基本性质二、概率的几个基本性质(3)、特别地,当事件A与事件B是对立事件时,有
P(A)=1- P(B)
3.1.3 概率的基本性质二、概率的几个基本性质利用上述的基本性质,可以简化概率的计算 互斥事件与对立事件的区别与联系,互斥事件是指事件A与事件B在一次试验中不会同时发生,其具体包括三种不同的情形:
(1)事件A发生且事件B不发生;
(2)事件A不发生且事件B发生;
(3)事件A与事件B同时不发生,
而对立事件是指事件A与事件B有且仅有一个发生,其包括两种情形;
(1)事件A发生B不发生;
(2)事件B发生事件A不发生,对立事件互斥事件的特殊情形。例1、抛掷色子,事件A= “朝上一面的数是奇数”,
事件B = “朝上一面的数不超过3”,
求P(A∪B)解法一:
因为P(A)=3/6=1/2,P(B)=3/6=1/2
所以P(A∪B)= P(A)+ P(B)=1解法二:
A∪B这一事件包括4种结果,即出现1,2,3和5
所以P(A∪B)= 4/6=2/3请判断那种正确!例2 如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是取到方块(事件B)的概率是 问:(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?分析:事件C是事件A与事件B的并,且A与B互斥,因此可用互斥事件的概率和公式求解,事件C与事件D是对立事件,因此P(D)=1—P(C).
解:(1)P(C)=P(A)+ P(B)=(2)P(D)=1—P(C)=概率的基本性质:
1)必然事件概率为1,不可能事件概率为0,因此0≤P(A)≤1;
2)当事件A与B互斥时,满足加法公式:P(A∪B)= P(A)+ P(B);
3)若事件A与B为对立事件,则A∪B为必然事件,所以P(A∪B)= P(A)+ P(B)=1,于是有P(A)=1—P(B);课本116页练习再见
的关系
和运算 概率的
几个基
本性质 一、 事件的关系和运算1.包含关系
2.相等关系
3.事件的并 (或和)
4.事件的交 (或积)
5.事件的互斥
6.对立事件
事件的运算事件的关系1、投掷一枚硬币,考察正面还是反面朝上.
A={正面朝上} ,B={反面朝上} A,B是对立事件 A,B是互斥(事件) 2、某人对靶射击一次,观察命中环数
A =“命中偶数环” B =“命中奇数环”
C =“命中 o 数环”A,B是互斥事件A,B是对立事件3、一名学生独立解答两道物理习题,考察这两道
习题的解答情况.
记 A = “该学生会解答第一题,不会解答第二题”
B = “该学生会解答第一题,还会解答第二题”
试回答:
1. 事件A 与事件B 互斥吗?为什么?
2. 事件A 与事件B 互为对立事件吗?为什么? 4、某检查员从一批产品中抽取8件进行检查,观察其中的次品数
记:A =“次品数少于5件” ; B = “次品数恰有2件”
C = “次品数多于3件” ; D = “次品数至少有1件”
试写出下列事件的基本事件组成:
A∪ B , A ∩C, B∩ C ;A∪B = A ( A,B 中至少有一个发生)A∩C= “有4件次品”一次抽取8件共有9种抽取结果;
第一种: 有 0 件次品(全是合格品),
第二种: 有 1 件次品(7件合格品),
第三种: 有 2 件次品(6件合格品),
第四种: 有 3 件次品(5件合格品),
第五种: 有 4 件次品(4件合格品),
第六种: 有 5 件次品(3件合格品),
第七种: 有 6 件次品(2件合格品),
第八种: 有 7 件次品(1件合格品),
第九种: 有 8 件次品(0件合格品).3.1.3 概率的基本性质二、概率的几个基本性质(1)、对于任何事件的概率的范围是:
0≤P(A)≤1
其中不可能事件的概率是P(A)=0
必然事件的概率是P(A)=1
不可能事件与必然事件是一般事件的特殊情况(2)、当事件A与事件B互斥时,A∪B的频率
fn(A∪B)= fn(A)+ fn(B)
由此得到概率的加法公式:
如果事件A与事件B互斥,则
P(A∪B)=P(A)+P(B)3.1.3 概率的基本性质二、概率的几个基本性质(3)、特别地,当事件A与事件B是对立事件时,有
P(A)=1- P(B)
3.1.3 概率的基本性质二、概率的几个基本性质利用上述的基本性质,可以简化概率的计算 互斥事件与对立事件的区别与联系,互斥事件是指事件A与事件B在一次试验中不会同时发生,其具体包括三种不同的情形:
(1)事件A发生且事件B不发生;
(2)事件A不发生且事件B发生;
(3)事件A与事件B同时不发生,
而对立事件是指事件A与事件B有且仅有一个发生,其包括两种情形;
(1)事件A发生B不发生;
(2)事件B发生事件A不发生,对立事件互斥事件的特殊情形。例1、抛掷色子,事件A= “朝上一面的数是奇数”,
事件B = “朝上一面的数不超过3”,
求P(A∪B)解法一:
因为P(A)=3/6=1/2,P(B)=3/6=1/2
所以P(A∪B)= P(A)+ P(B)=1解法二:
A∪B这一事件包括4种结果,即出现1,2,3和5
所以P(A∪B)= 4/6=2/3请判断那种正确!例2 如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是取到方块(事件B)的概率是 问:(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?分析:事件C是事件A与事件B的并,且A与B互斥,因此可用互斥事件的概率和公式求解,事件C与事件D是对立事件,因此P(D)=1—P(C).
解:(1)P(C)=P(A)+ P(B)=(2)P(D)=1—P(C)=概率的基本性质:
1)必然事件概率为1,不可能事件概率为0,因此0≤P(A)≤1;
2)当事件A与B互斥时,满足加法公式:P(A∪B)= P(A)+ P(B);
3)若事件A与B为对立事件,则A∪B为必然事件,所以P(A∪B)= P(A)+ P(B)=1,于是有P(A)=1—P(B);课本116页练习再见
