解与视角有关的直角三角形
文档属性
| 名称 | 解与视角有关的直角三角形 |

|
|
| 格式 | zip | ||
| 文件大小 | 504.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-28 00:00:00 | ||
图片预览

文档简介
“一·三·六”导学案——九年级数学(下)
编号:2806 班级: 姓名:
课题:解与视角有关的直角三角形
主备: 审核: 时间: 年 月 日
【明确目标】
1.进一步掌握锐角三角函数的概念,熟练运用仰角、俯角等知识解直角三角形及解某些实际问题.
2.经历测量仰角、俯角的方法解决实际问题的过程,运用数形结合思想和建模思想解决实际问题.
3.通过学习,体验数形结合思想和培养数学的应用意识.
【自主预习】
一、新课引入
在现实生活中,有很多地方会应用解直角三角形的知识来解决问题.今天我们将学习圆与解直角三角形和仰角、俯角与解直角三角形的综合解答题.
二、预习导学
阅读教材P74~75,自学“例3”与“例4”,复习圆的切线相关的知识,弄清仰角与俯角的概念,并尝试完成自主预习区.
1.在Rt△ABC中,∠C=90°,AC=5,BC=12,则AB=__________.
2.在Rt△ABC中,∠C=90°,a=15,c=,则∠A=__________.
【合作探究】
活动1 新知探究
知识点一:解直角三角形在圆中的应用
(1)学生自主学习教材P74例3.
(2)学生代表讲述对例3的理解和解题方法.
(3)教师矫正和强化.
知识点二:仰角、俯角在解直角三角形中的应用
(1)学生自主学习教材P75例4.
(2)小组交流对仰角和俯角的认识.
(3)师生交流对例4的理解和解题方法.
活动2 新知应用
小组讨论合作交流
例1 如图所示,厂房屋顶人字架(等腰三角形)的跨度为10m,∠A=26°,求中柱BC(C为底边中点)和上弦AB的长.(精确到0.01m)
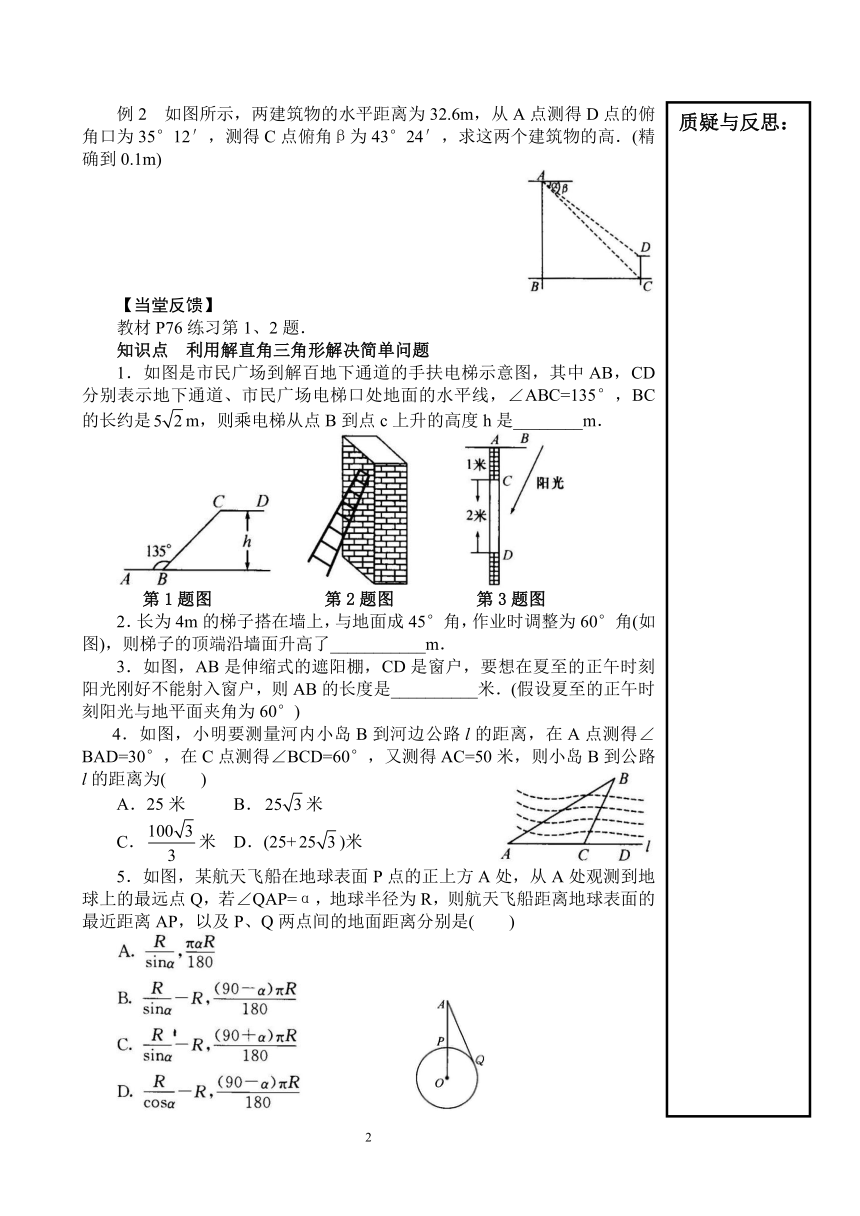
例2 如图所示,两建筑物的水平距离为32.6m,从A点测得D点的俯角口为35°12′,测得C点俯角β为43°24′,求这两个建筑物的高.(精确到0.1m)
【当堂反馈】
教材P76练习第1、2题.
知识点 利用解直角三角形解决简单问题
1.如图是市民广场到解百地下通道的手扶电梯示意图,其中AB,CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是m,则乘电梯从点B到点c上升的高度h是________m.
第1题图 第2题图 第3题图
2.长为4m的梯子搭在墙上,与地面成45°角,作业时调整为60°角(如图),则梯子的顶端沿墙面升高了___________m.
3.如图,AB是伸缩式的遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB的长度是__________米.(假设夏至的正午时刻阳光与地平面夹角为60°)
4.如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路l的距离为( )
A.25米 B.米
C.米 D.(25+)米
5.如图,某航天飞船在地球表面P点的正上方A处,从A处观测到地球上的最远点Q,若∠QAP=α,地球半径为R,则航天飞船距离地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( )
【拓展提升】
1.教材P77习题28.2第3、4、5题,复习题28第8题(必做).
2.如图所示,一只运载火箭从地面L处发射,当卫星到达A点时,从位于地面R处的雷达站测得AR的距离是6km,仰角为43°,1s后,火箭到达B点,此时测得BR的距离是6.13km,仰角为45.54°,这个火箭从A到B的平均速度是多少(精确到0.01km/s)?
3.如图所示,在小山BD上有一座塔,塔的高度BC=20m,在河的岸边有一点A,A、D在同一水平地面上,在A处测得塔底B的仰角为60°,塔顶C的仰角为66°.
你能根据以上的数据求出小山的高.BD吗?若不能,请说明理由;若能,请求出小山的高BD.(精确到0.1m)(选做)
【课后检测】
一、选择题
1.身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
A.甲 B.乙 C.丙 D.丁 第2题图
2.将宽为2cm的长方形纸条折叠成如图所示的形状,那么折痕PQ的长是( )
A.cm B.cm C.cm D.2cm
二、填空题
3.在207国道襄阳段改造工程中,需沿AC方向开山修路(如图所示),为了加快施工速度,需要在小山的另一边同时施工.从AC上的一点B取∠ABD=140°,BD=1000m,∠D=50°.为了使开挖点E在直线AC上,那么DE=__________m.(供选用的三角函数值:sin50°≈0.7660,cos50°≈0.6428,tan50°≈1.192)
4.如图,将45°的∠AOB按上面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰好为2cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为_______cm.(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
三、解答题
5.如图,∠MON=25°,矩形ABCD的对角线AC⊥ON,边BC在OM上,当AC=3时,AD的长是多少?(结果精确到0.01)
6.如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的∠CDO=51°18′,求梯子的长.
(参考数据:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)
7.某学校的校门是伸缩门(如图1),伸缩门中的每一行有20个菱形,每个菱形边长为30厘米.校门关闭时,每个菱形的锐角度数为60°(如图2);校门打开时,每个菱形的锐角度数从60°缩小为10°(如图3).
问:校门打开了多少米?(结果精确到1米,参考数据:sin5°≈0.0872,cos5°≈0.9962,sinl0°≈0.1736,cosl0°≈0.9848)
编号:2806 班级: 姓名:
课题:解与视角有关的直角三角形
主备: 审核: 时间: 年 月 日
【明确目标】
1.进一步掌握锐角三角函数的概念,熟练运用仰角、俯角等知识解直角三角形及解某些实际问题.
2.经历测量仰角、俯角的方法解决实际问题的过程,运用数形结合思想和建模思想解决实际问题.
3.通过学习,体验数形结合思想和培养数学的应用意识.
【自主预习】
一、新课引入
在现实生活中,有很多地方会应用解直角三角形的知识来解决问题.今天我们将学习圆与解直角三角形和仰角、俯角与解直角三角形的综合解答题.
二、预习导学
阅读教材P74~75,自学“例3”与“例4”,复习圆的切线相关的知识,弄清仰角与俯角的概念,并尝试完成自主预习区.
1.在Rt△ABC中,∠C=90°,AC=5,BC=12,则AB=__________.
2.在Rt△ABC中,∠C=90°,a=15,c=,则∠A=__________.
【合作探究】
活动1 新知探究
知识点一:解直角三角形在圆中的应用
(1)学生自主学习教材P74例3.
(2)学生代表讲述对例3的理解和解题方法.
(3)教师矫正和强化.
知识点二:仰角、俯角在解直角三角形中的应用
(1)学生自主学习教材P75例4.
(2)小组交流对仰角和俯角的认识.
(3)师生交流对例4的理解和解题方法.
活动2 新知应用
小组讨论合作交流
例1 如图所示,厂房屋顶人字架(等腰三角形)的跨度为10m,∠A=26°,求中柱BC(C为底边中点)和上弦AB的长.(精确到0.01m)
例2 如图所示,两建筑物的水平距离为32.6m,从A点测得D点的俯角口为35°12′,测得C点俯角β为43°24′,求这两个建筑物的高.(精确到0.1m)
【当堂反馈】
教材P76练习第1、2题.
知识点 利用解直角三角形解决简单问题
1.如图是市民广场到解百地下通道的手扶电梯示意图,其中AB,CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是m,则乘电梯从点B到点c上升的高度h是________m.
第1题图 第2题图 第3题图
2.长为4m的梯子搭在墙上,与地面成45°角,作业时调整为60°角(如图),则梯子的顶端沿墙面升高了___________m.
3.如图,AB是伸缩式的遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB的长度是__________米.(假设夏至的正午时刻阳光与地平面夹角为60°)
4.如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路l的距离为( )
A.25米 B.米
C.米 D.(25+)米
5.如图,某航天飞船在地球表面P点的正上方A处,从A处观测到地球上的最远点Q,若∠QAP=α,地球半径为R,则航天飞船距离地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( )
【拓展提升】
1.教材P77习题28.2第3、4、5题,复习题28第8题(必做).
2.如图所示,一只运载火箭从地面L处发射,当卫星到达A点时,从位于地面R处的雷达站测得AR的距离是6km,仰角为43°,1s后,火箭到达B点,此时测得BR的距离是6.13km,仰角为45.54°,这个火箭从A到B的平均速度是多少(精确到0.01km/s)?
3.如图所示,在小山BD上有一座塔,塔的高度BC=20m,在河的岸边有一点A,A、D在同一水平地面上,在A处测得塔底B的仰角为60°,塔顶C的仰角为66°.
你能根据以上的数据求出小山的高.BD吗?若不能,请说明理由;若能,请求出小山的高BD.(精确到0.1m)(选做)
【课后检测】
一、选择题
1.身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
A.甲 B.乙 C.丙 D.丁 第2题图
2.将宽为2cm的长方形纸条折叠成如图所示的形状,那么折痕PQ的长是( )
A.cm B.cm C.cm D.2cm
二、填空题
3.在207国道襄阳段改造工程中,需沿AC方向开山修路(如图所示),为了加快施工速度,需要在小山的另一边同时施工.从AC上的一点B取∠ABD=140°,BD=1000m,∠D=50°.为了使开挖点E在直线AC上,那么DE=__________m.(供选用的三角函数值:sin50°≈0.7660,cos50°≈0.6428,tan50°≈1.192)
4.如图,将45°的∠AOB按上面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰好为2cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为_______cm.(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
三、解答题
5.如图,∠MON=25°,矩形ABCD的对角线AC⊥ON,边BC在OM上,当AC=3时,AD的长是多少?(结果精确到0.01)
6.如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的∠CDO=51°18′,求梯子的长.
(参考数据:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)
7.某学校的校门是伸缩门(如图1),伸缩门中的每一行有20个菱形,每个菱形边长为30厘米.校门关闭时,每个菱形的锐角度数为60°(如图2);校门打开时,每个菱形的锐角度数从60°缩小为10°(如图3).
问:校门打开了多少米?(结果精确到1米,参考数据:sin5°≈0.0872,cos5°≈0.9962,sinl0°≈0.1736,cosl0°≈0.9848)
