九年级数学下册试题 6.3相似图形同步练习-苏科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 6.3相似图形同步练习-苏科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 184.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 19:45:44 | ||
图片预览



文档简介
6.3相似图形
一.选择题
1. 若某个直角三角形的两直角边之比为2:3,则确定了该三角形的( )
A.形状 B.周长 C.面积 D.斜边
2. 下列图形中一定是相似形的是( )
A.两个等边三角形 B.两个菱形
C.两个矩形 D.两个直角三角形
3. 将直角三角形的三条边的长度都扩大同样的倍数后得到的三角形( )
A.仍是直角三角形 B.一定是锐角三角形
C.可能是钝角三角形 D.一定是钝角三角形
4. 分别画出下列四组图形,必是相似三角形的为( )
A.两个直角三角形
B.有一个角为110°的两个等腰三角形
C.有一个角为55°的两个等腰三角形
D.两条边对应成比例,其中一边的对角对应相等的两个三角形
5. 下列各组图形中,是相似图形的是( )
A. B.
C. D.
6. 下面四组图形中,必是相似三角形的为( )
A.两个直角三角形
B.两条边对应成比例,一个对应角相等的两个三角形
C.有一个角为40°的两个等腰三角形
D.有一个角为100°的两个等腰三角形
7. 下列说法正确的是( )
A.对应边都成比例的多边形相似
B.对应角都相等的多边形相似
C.边数相同的正多边形相似
D.矩形都相似
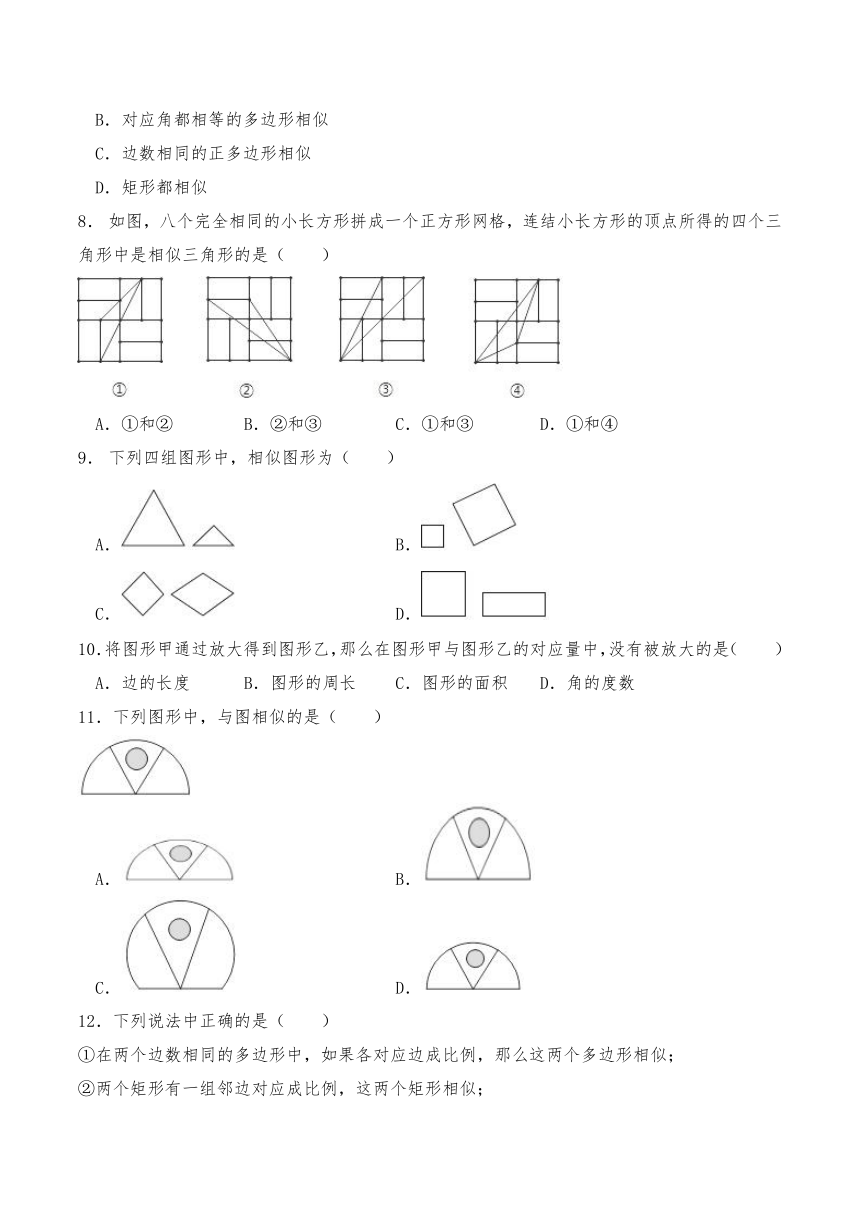
8. 如图,八个完全相同的小长方形拼成一个正方形网格,连结小长方形的顶点所得的四个三角形中是相似三角形的是( )
A.①和② B.②和③ C.①和③ D.①和④
9. 下列四组图形中,相似图形为( )
A. B.
C. D.
10.将图形甲通过放大得到图形乙,那么在图形甲与图形乙的对应量中,没有被放大的是( )
A.边的长度 B.图形的周长 C.图形的面积 D.角的度数
11.下列图形中,与图相似的是( )
A. B.
C. D.
12.下列说法中正确的是( )
①在两个边数相同的多边形中,如果各对应边成比例,那么这两个多边形相似;
②两个矩形有一组邻边对应成比例,这两个矩形相似;
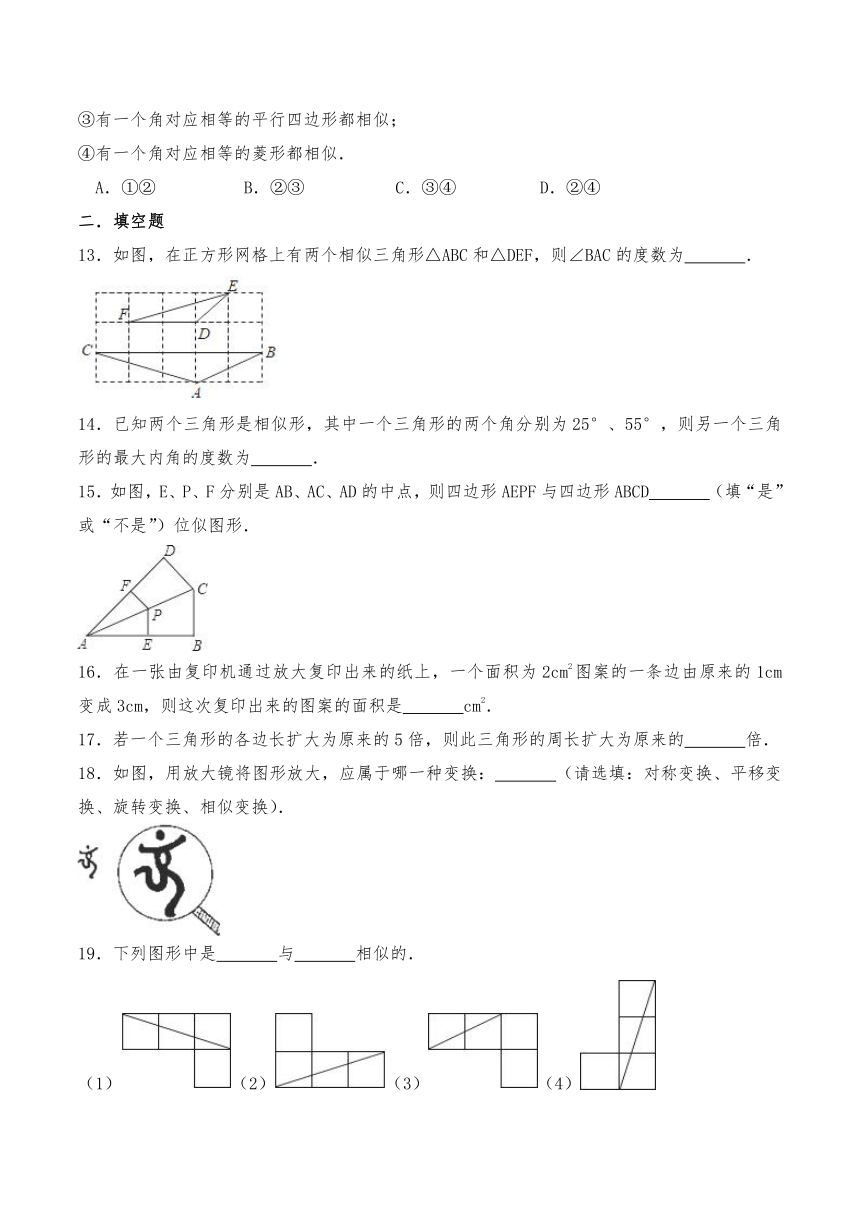
③有一个角对应相等的平行四边形都相似;
④有一个角对应相等的菱形都相似.
A.①② B.②③ C.③④ D.②④
二.填空题
13.如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为 .
14.已知两个三角形是相似形,其中一个三角形的两个角分别为25°、55°,则另一个三角形的最大内角的度数为 .
15.如图,E、P、F分别是AB、AC、AD的中点,则四边形AEPF与四边形ABCD (填“是”或“不是”)位似图形.
16.在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,则这次复印出来的图案的面积是 cm2.
17.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 倍.
18.如图,用放大镜将图形放大,应属于哪一种变换: (请选填:对称变换、平移变换、旋转变换、相似变换).
19.下列图形中是 与 相似的.
(1)(2)(3)(4)
20.如图,在Rt△ACB中,∠ABC=90°,D为BC边的中点,BE⊥AD于点E,交AC于F,若AB=4,BC=6,则线段EF的长为 .
21.挂在墙上的中国地图与课本上的中国地图 相似的图形.
22.请从以下两个小题中任选一个作答,若多选,则按所选的第一小题计分.
(1)方程x2﹣9x+18=0的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为
(2)如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应平行,且对应边之间的距离都相等,那么两个图形不相似的一组是(请填写正确答案的序号) .
三.解答题
23.设四边形ABCD与四边形EFGH是相似图形.且A与E,B与F,C与G,D与H是对应点.已知AB=10.BC=8,CD=8,AD=6,EF=8,求四边形EFGH的周长.
24.如图所示,小芳用画正方形的办法画出下列一组图案,你能按规律继续画下去吗?想想其中有哪些相似图形?
25.某校九年级数学兴趣小组在探究相似多边形问题时,他们提出了下面两个观点:
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们对应的边间距都为1,则新三角形与原三角形相似.
观点二:将邻边为6和10的矩形按图2的方式向内缩小,得到新的矩形,它们对应的边间距都为1,则新矩形与原矩形相似.
请回答下列问题:
(1)你认为上述两个观点是否正确?请说明理由.
(2)如图3,已知△ABC,AC=6,BC=8,AB=10,将△ABC按图3的方式向外扩张,得到△DEF,它们对应的边间距都为m,DE=15,求△DEF的面积.
26.如图,四边形ABCD与四边形A'B'C'D'相似的图形,点A与点A′、点B与点B′、点C与点C′、点D与点D′分别是对应顶点,已知数据如图所示,求未知边x、y的长度和角α、β的大小.
27.已知四边形ABCD和四边形A'B'C'D'是相似的图形,并且点A与点A'、点B与点B'、点C与点C'、点D与点D'分别是对应顶点,已知BC=4,CD=3.6,A'B'=3.3,B'C'=3,∠B=75°,∠C=105°,∠D=95°,求AB,C'D'的长和∠A'的度数.
28.观察下列的图形(a)﹣(g),其中哪些是与图形(1)、(2)或(3)相似的.
与图形(1)相似的有 ;(填序号)
与图形(2)相似的有 ;
与图形(3)相似的有 .
29.如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形越接近于正方形.
①若菱形的一个内角为70°,则该菱形的“接近度”等于 ;
②当菱形的“接近度”等于 时,菱形是正方形.
(2)设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a﹣b|,于是|a﹣b|越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
30.阅读下面的短文,并解答下列问题:
我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同.就把它们叫做相似体.
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比:a:b,设S甲:S乙分别表示这两个正方体的表面积,则,又设V甲、V乙分别表示这两个正方体的体积,则.
(1)下列几何体中,一定属于相似体的是 A.两个球体;B.两个圆锥体;C.两个圆柱体;D.两个长方体.
(2)请归纳出相似体的3条主要性质:
①相似体的一切对应线段(或弧)长的比等于 ;
②相似体表面积的比等于 ;
③相似体体积的比等于 .
答案
一.选择题
A.A.A.B.D.D.C.D.B.D.D.D.
二.填空题
13.135°.
14.100°.
15.是.
16.18.
17.5.
18.相似变换
19.(1)与(4)
20..
21.是
22.②.
三.解答题
23.四边形ABCD的周长=AB+BC+CD+AD=10+8+8+6=32,
∵四边形ABCD与四边形EEGH是相似图形,
∴四边形ABCD的周长:四边形EEGH的周长=AB:EF,
∴四边形EEGH的周长32=25.6.
24.这组图形的规律是:后面的图案比前面的图案多两个全等的正方形,且多出的这两个正方形的边长等于前面正方形对角线的长.按此规律可以继续画图.其中每两个全等的正方形组成的图形与后面多出的两个全等的正方形形成的图形都是相似的.
25.(1)观点一正确;观点二不正确.
理由:①如图(1)连接并延长DA,交FC的延长线于点O,
∵△ABC和△DEF对应的边的距离都为1,
∴AB∥DE,AC∥DF,
∴∠FDO=∠CAO,∠ODE=∠OAB,
∴∠FDO+∠ODE=∠CAO+∠OAB,
即∠FDE=∠CAB,同理∠DEF=∠ABC,
∴△ABC∽△DEF,
∴观点一正确;
②如图(2)由题意可知,原矩形的邻边为6和10,
则新矩形邻边为4和8,
∵,,
∴,
∴新矩形于原矩形不相似,
∴观点二不正确;
(2)如图(3),延长DA、EB交于点O,
∵A到DE、DF的距离都为1,
∴DA是∠FDE的角平分线,
同理,EB是∠DEF的角平分线,
∴点O是△ABC的内心,
∵AC=6,BC=8,AB=10,
∴△ABC是直角三角形,
设△ABC的内切圆的半径为r,
则6﹣r+8﹣r=10,
解得r=2,
过点O作OH⊥DE于点H,交AB于G,
∵AB∥DE,
∴OG⊥AB,
∴OG=r=2,
∴,
同理,
∴DF=9,EF=12,
∴△DEF的面积为:9×12=54.
26.在四边形ABCD中,∠D=∠D'=β=55°,
∠A=α=360°﹣55°﹣90°﹣60°=155°,
∵四边形ABCD∽四边形A'B'C'D',
∴,
∴x=6,y=15.
27.在四边形ABCD中,∠A=360°﹣75°﹣105°﹣95°=85°,
∵四边形ABCD∽四边形A'B'C'D',
∴AB:A′B′=CD:C′D′=BC:B′C′=4:3,∠A′=∠A=85°,
∵A′B′=3.3,CD=3.6,
∴AB=4.4.C′D′=2.7,
28.观察比较图形,根据相似形的定义可知:
与图形(1)相似的有a;
与图形(2)相似的有d;
与图形(3)相似的有g.
29.(1)①∵内角为70°,
∴与它相邻内角的度数为110°.
∴菱形的“接近度”=|m﹣n|=|110﹣70|=40.
②当菱形的“接近度”等于0时,菱形是正方形.
(2)不合理.
例如,对两个相似而不全等的矩形来说,它们接近正方形的程度是相同的,但|a﹣b|却不相等.
合理定义方法不唯一.
如定义为,
越接近1,矩形越接近于正方形;
越大,矩形与正方形的形状差异越大;
当时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.
30.(1)A 两个球体,形状完全相同,是相似体.
B两个圆锥体,如果底面半径或高发生变化,图形就会改变,不是相似体.
C 两个圆柱体,如果底面半径或高发生变化,图形就会改变,不是相似体.
D 两个长方体,如果长,宽,高中有一个发生变化,图形就会改变,不是相似体.
故选A.
(2)根据阅读材料进行归纳可以得到:
①相似体的一切对应线段(或弧)长的比等于相似比.
②相似体表面积的比等于相似比的平方.
③相似体体积的比等于相似比的立方.
故答案为(1)A.(2)①相似比;②相似比的平方;③相似比的立方.
一.选择题
1. 若某个直角三角形的两直角边之比为2:3,则确定了该三角形的( )
A.形状 B.周长 C.面积 D.斜边
2. 下列图形中一定是相似形的是( )
A.两个等边三角形 B.两个菱形
C.两个矩形 D.两个直角三角形
3. 将直角三角形的三条边的长度都扩大同样的倍数后得到的三角形( )
A.仍是直角三角形 B.一定是锐角三角形
C.可能是钝角三角形 D.一定是钝角三角形
4. 分别画出下列四组图形,必是相似三角形的为( )
A.两个直角三角形
B.有一个角为110°的两个等腰三角形
C.有一个角为55°的两个等腰三角形
D.两条边对应成比例,其中一边的对角对应相等的两个三角形
5. 下列各组图形中,是相似图形的是( )
A. B.
C. D.
6. 下面四组图形中,必是相似三角形的为( )
A.两个直角三角形
B.两条边对应成比例,一个对应角相等的两个三角形
C.有一个角为40°的两个等腰三角形
D.有一个角为100°的两个等腰三角形
7. 下列说法正确的是( )
A.对应边都成比例的多边形相似
B.对应角都相等的多边形相似
C.边数相同的正多边形相似
D.矩形都相似
8. 如图,八个完全相同的小长方形拼成一个正方形网格,连结小长方形的顶点所得的四个三角形中是相似三角形的是( )
A.①和② B.②和③ C.①和③ D.①和④
9. 下列四组图形中,相似图形为( )
A. B.
C. D.
10.将图形甲通过放大得到图形乙,那么在图形甲与图形乙的对应量中,没有被放大的是( )
A.边的长度 B.图形的周长 C.图形的面积 D.角的度数
11.下列图形中,与图相似的是( )
A. B.
C. D.
12.下列说法中正确的是( )
①在两个边数相同的多边形中,如果各对应边成比例,那么这两个多边形相似;
②两个矩形有一组邻边对应成比例,这两个矩形相似;
③有一个角对应相等的平行四边形都相似;
④有一个角对应相等的菱形都相似.
A.①② B.②③ C.③④ D.②④
二.填空题
13.如图,在正方形网格上有两个相似三角形△ABC和△DEF,则∠BAC的度数为 .
14.已知两个三角形是相似形,其中一个三角形的两个角分别为25°、55°,则另一个三角形的最大内角的度数为 .
15.如图,E、P、F分别是AB、AC、AD的中点,则四边形AEPF与四边形ABCD (填“是”或“不是”)位似图形.
16.在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,则这次复印出来的图案的面积是 cm2.
17.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 倍.
18.如图,用放大镜将图形放大,应属于哪一种变换: (请选填:对称变换、平移变换、旋转变换、相似变换).
19.下列图形中是 与 相似的.
(1)(2)(3)(4)
20.如图,在Rt△ACB中,∠ABC=90°,D为BC边的中点,BE⊥AD于点E,交AC于F,若AB=4,BC=6,则线段EF的长为 .
21.挂在墙上的中国地图与课本上的中国地图 相似的图形.
22.请从以下两个小题中任选一个作答,若多选,则按所选的第一小题计分.
(1)方程x2﹣9x+18=0的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为
(2)如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应平行,且对应边之间的距离都相等,那么两个图形不相似的一组是(请填写正确答案的序号) .
三.解答题
23.设四边形ABCD与四边形EFGH是相似图形.且A与E,B与F,C与G,D与H是对应点.已知AB=10.BC=8,CD=8,AD=6,EF=8,求四边形EFGH的周长.
24.如图所示,小芳用画正方形的办法画出下列一组图案,你能按规律继续画下去吗?想想其中有哪些相似图形?
25.某校九年级数学兴趣小组在探究相似多边形问题时,他们提出了下面两个观点:
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们对应的边间距都为1,则新三角形与原三角形相似.
观点二:将邻边为6和10的矩形按图2的方式向内缩小,得到新的矩形,它们对应的边间距都为1,则新矩形与原矩形相似.
请回答下列问题:
(1)你认为上述两个观点是否正确?请说明理由.
(2)如图3,已知△ABC,AC=6,BC=8,AB=10,将△ABC按图3的方式向外扩张,得到△DEF,它们对应的边间距都为m,DE=15,求△DEF的面积.
26.如图,四边形ABCD与四边形A'B'C'D'相似的图形,点A与点A′、点B与点B′、点C与点C′、点D与点D′分别是对应顶点,已知数据如图所示,求未知边x、y的长度和角α、β的大小.
27.已知四边形ABCD和四边形A'B'C'D'是相似的图形,并且点A与点A'、点B与点B'、点C与点C'、点D与点D'分别是对应顶点,已知BC=4,CD=3.6,A'B'=3.3,B'C'=3,∠B=75°,∠C=105°,∠D=95°,求AB,C'D'的长和∠A'的度数.
28.观察下列的图形(a)﹣(g),其中哪些是与图形(1)、(2)或(3)相似的.
与图形(1)相似的有 ;(填序号)
与图形(2)相似的有 ;
与图形(3)相似的有 .
29.如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形越接近于正方形.
①若菱形的一个内角为70°,则该菱形的“接近度”等于 ;
②当菱形的“接近度”等于 时,菱形是正方形.
(2)设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a﹣b|,于是|a﹣b|越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
30.阅读下面的短文,并解答下列问题:
我们把相似形的概念推广到空间:如果两个几何体大小不一定相等,但形状完全相同.就把它们叫做相似体.
如图,甲、乙是两个不同的正方体,正方体都是相似体,它们的一切对应线段之比都等于相似比:a:b,设S甲:S乙分别表示这两个正方体的表面积,则,又设V甲、V乙分别表示这两个正方体的体积,则.
(1)下列几何体中,一定属于相似体的是 A.两个球体;B.两个圆锥体;C.两个圆柱体;D.两个长方体.
(2)请归纳出相似体的3条主要性质:
①相似体的一切对应线段(或弧)长的比等于 ;
②相似体表面积的比等于 ;
③相似体体积的比等于 .
答案
一.选择题
A.A.A.B.D.D.C.D.B.D.D.D.
二.填空题
13.135°.
14.100°.
15.是.
16.18.
17.5.
18.相似变换
19.(1)与(4)
20..
21.是
22.②.
三.解答题
23.四边形ABCD的周长=AB+BC+CD+AD=10+8+8+6=32,
∵四边形ABCD与四边形EEGH是相似图形,
∴四边形ABCD的周长:四边形EEGH的周长=AB:EF,
∴四边形EEGH的周长32=25.6.
24.这组图形的规律是:后面的图案比前面的图案多两个全等的正方形,且多出的这两个正方形的边长等于前面正方形对角线的长.按此规律可以继续画图.其中每两个全等的正方形组成的图形与后面多出的两个全等的正方形形成的图形都是相似的.
25.(1)观点一正确;观点二不正确.
理由:①如图(1)连接并延长DA,交FC的延长线于点O,
∵△ABC和△DEF对应的边的距离都为1,
∴AB∥DE,AC∥DF,
∴∠FDO=∠CAO,∠ODE=∠OAB,
∴∠FDO+∠ODE=∠CAO+∠OAB,
即∠FDE=∠CAB,同理∠DEF=∠ABC,
∴△ABC∽△DEF,
∴观点一正确;
②如图(2)由题意可知,原矩形的邻边为6和10,
则新矩形邻边为4和8,
∵,,
∴,
∴新矩形于原矩形不相似,
∴观点二不正确;
(2)如图(3),延长DA、EB交于点O,
∵A到DE、DF的距离都为1,
∴DA是∠FDE的角平分线,
同理,EB是∠DEF的角平分线,
∴点O是△ABC的内心,
∵AC=6,BC=8,AB=10,
∴△ABC是直角三角形,
设△ABC的内切圆的半径为r,
则6﹣r+8﹣r=10,
解得r=2,
过点O作OH⊥DE于点H,交AB于G,
∵AB∥DE,
∴OG⊥AB,
∴OG=r=2,
∴,
同理,
∴DF=9,EF=12,
∴△DEF的面积为:9×12=54.
26.在四边形ABCD中,∠D=∠D'=β=55°,
∠A=α=360°﹣55°﹣90°﹣60°=155°,
∵四边形ABCD∽四边形A'B'C'D',
∴,
∴x=6,y=15.
27.在四边形ABCD中,∠A=360°﹣75°﹣105°﹣95°=85°,
∵四边形ABCD∽四边形A'B'C'D',
∴AB:A′B′=CD:C′D′=BC:B′C′=4:3,∠A′=∠A=85°,
∵A′B′=3.3,CD=3.6,
∴AB=4.4.C′D′=2.7,
28.观察比较图形,根据相似形的定义可知:
与图形(1)相似的有a;
与图形(2)相似的有d;
与图形(3)相似的有g.
29.(1)①∵内角为70°,
∴与它相邻内角的度数为110°.
∴菱形的“接近度”=|m﹣n|=|110﹣70|=40.
②当菱形的“接近度”等于0时,菱形是正方形.
(2)不合理.
例如,对两个相似而不全等的矩形来说,它们接近正方形的程度是相同的,但|a﹣b|却不相等.
合理定义方法不唯一.
如定义为,
越接近1,矩形越接近于正方形;
越大,矩形与正方形的形状差异越大;
当时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.
30.(1)A 两个球体,形状完全相同,是相似体.
B两个圆锥体,如果底面半径或高发生变化,图形就会改变,不是相似体.
C 两个圆柱体,如果底面半径或高发生变化,图形就会改变,不是相似体.
D 两个长方体,如果长,宽,高中有一个发生变化,图形就会改变,不是相似体.
故选A.
(2)根据阅读材料进行归纳可以得到:
①相似体的一切对应线段(或弧)长的比等于相似比.
②相似体表面积的比等于相似比的平方.
③相似体体积的比等于相似比的立方.
故答案为(1)A.(2)①相似比;②相似比的平方;③相似比的立方.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
