九年级数学下册试题 6.4探索三角形相似的条件同步练习-苏科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 6.4探索三角形相似的条件同步练习-苏科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 192.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 19:45:00 | ||
图片预览



文档简介
6.4探索三角形相似的条件
一.选择题
1. 如图.在△ABC中,DE∥BC,∠B=∠ACD,则图中相似三角形有( )
A.2对 B.3对 C.4对 D.5对
2. 如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与点A、C重合),DE与AB相交于点F,那么与△BFD相似的三角形是( )
A.△BFE B.△BDC C.△BDA D.△AFD
3. 如图,在Rt△ACB中,∠ACB=90°,AC=BC,点D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE,则图中与△ACE全等或相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
4. 如图,在△ABC中,∠B=70°,AB=4,BC=6,将△ABC沿图示中的虚线DE剪开,剪下的三角形与原三角形不相似的是( )
A. B.
C. D.
5.如图,在△ABC中,AB=AC=8,BC=6,点P从点B出发以1个单位/s的速度向点A运动,同时点Q从点C出发以2个单位/s的速度向点B运动.当以B,P,Q为顶点的三角形与△ABC相似时,运动时间为( )
A.s B.s C.s或s D.以上均不对
6. 已知△ABC是正三角形,点D是边AC上一动点(不与A、C重合),以BD为边作正△BDE,边DE与边AB交于点F,则图中一定相似的三角形有( )对.
A.6 B.5 C.4 D.3
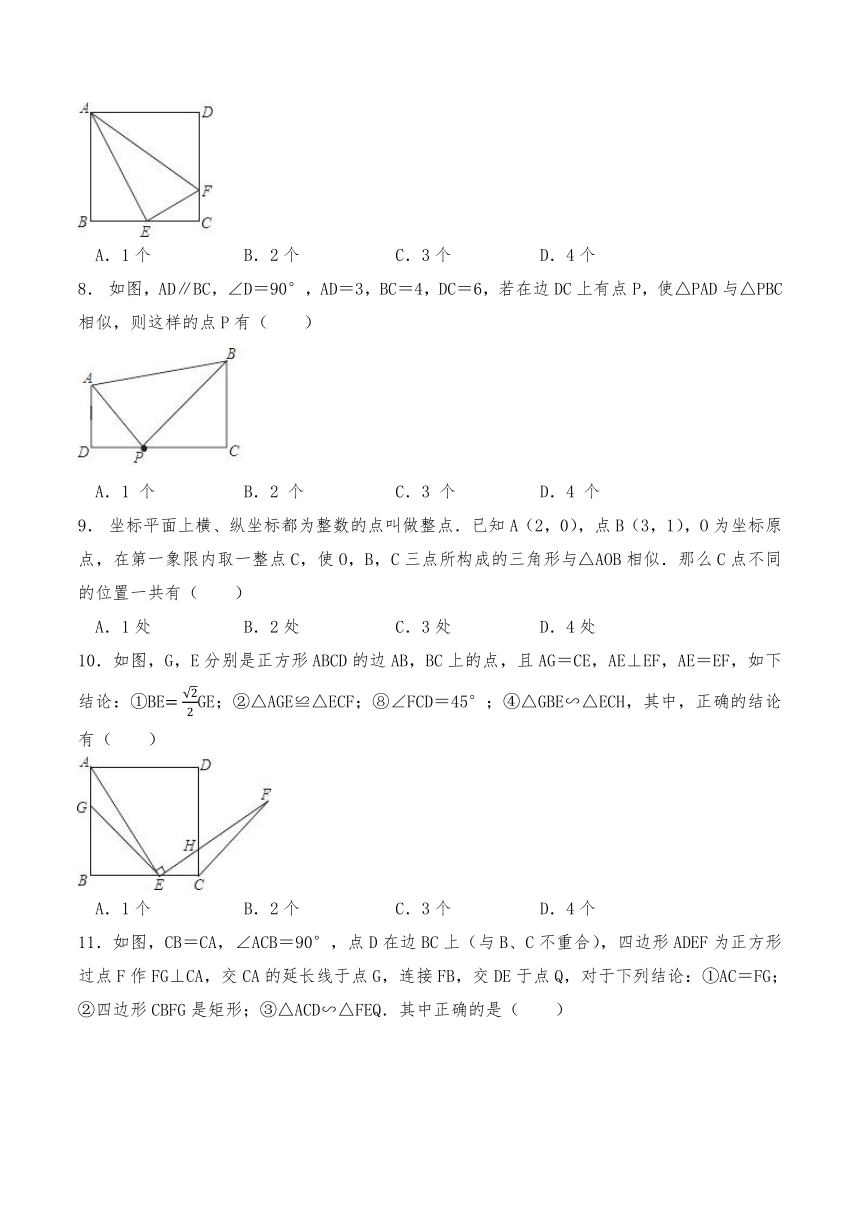
7. 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则下列结论正确的有( )
①∠BAE=30°;②CE2=AB CF;③CFCD;④△ABE∽△AEF.
A.1个 B.2个 C.3个 D.4个
8. 如图,AD∥BC,∠D=90°,AD=3,BC=4,DC=6,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有( )
A.1 个 B.2 个 C.3 个 D.4 个
9. 坐标平面上横、纵坐标都为整数的点叫做整点.已知A(2,0),点B(3,1),O为坐标原点,在第一象限内取一整点C,使O,B,C三点所构成的三角形与△AOB相似.那么C点不同的位置一共有( )
A.1处 B.2处 C.3处 D.4处
10.如图,G,E分别是正方形ABCD的边AB,BC上的点,且AG=CE,AE⊥EF,AE=EF,如下结论:①BEGE;②△AGE≌△ECF;⑧∠FCD=45°;④△GBE∽△ECH,其中,正确的结论有( )
A.1个 B.2个 C.3个 D.4个
11.如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,对于下列结论:①AC=FG;②四边形CBFG是矩形;③△ACD∽△FEQ.其中正确的是( )
A.①②③ B.①② C.①③ D.②③
二.填空题
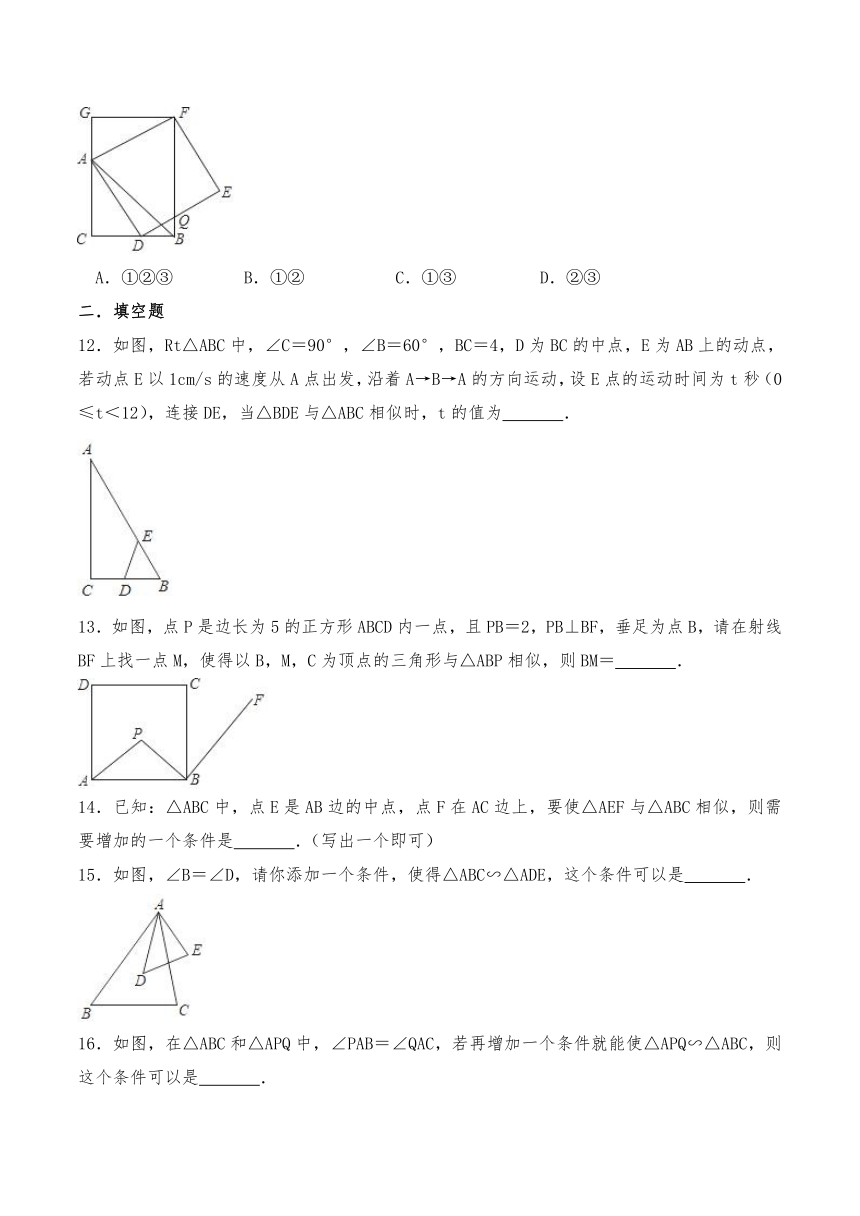
12.如图,Rt△ABC中,∠C=90°,∠B=60°,BC=4,D为BC的中点,E为AB上的动点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE与△ABC相似时,t的值为 .
13.如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM= .
14.已知:△ABC中,点E是AB边的中点,点F在AC边上,要使△AEF与△ABC相似,则需要增加的一个条件是 .(写出一个即可)
15.如图,∠B=∠D,请你添加一个条件,使得△ABC∽△ADE,这个条件可以是 .
16.如图,在△ABC和△APQ中,∠PAB=∠QAC,若再增加一个条件就能使△APQ∽△ABC,则这个条件可以是 .
17.如图,点P是△ABC中AB边上的 点,请你添加 个条件使△ACP∽△ABC: .
18.如图,在边长为4的正方形ABCD中,点E、F分别是BC、CD的中点,DE、AF交于点G,AF的中点为H,连接BG、DH.给出下列结论:
①AF⊥DE;②DG;③HD∥BG;④△ABG∽△DHF.
其中正确的结论有 .(请填上所有正确结论的序号)
19.如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△A1B1C1,当C,B1,C1三点共线时,旋转角为α,连接BB1,交于AC于点D,下面结论:
①△AC1C为等腰三角形;②CA=CB1;③α=135°;④△AB1D∽△ACB1;⑤中,正确的结论的序号为 .
20.如图,在Rt△ABC中,∠C=90°,AB=5,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则BD的长为 .
21.如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P是线段AD上的动点,过P作PF⊥AE于F,当以点P、F、E为顶点的三角形与△ABE相似时,AP的长为 .
22.如图,四边形ABCD中,∠A=∠B=90°,AB=5cm,AD=3cm,BC=2cm,P是AB上一点,若以P、A、D为顶点的三角形与△PBC相似,则PA= cm.
23.如图,等腰△ABC中,AB=AC=5,BC=8,点F是边BC上不与点B,C重合的一个动点,直线DE垂直平分BF,垂足为D.当△ACF是直角三角形时,BD的长为 .
三.解答题
24.如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动,当其中一点到达终点时,另一点也随之停止运动.
(1)如果点P,Q同时出发,经过几秒钟时△PCQ的面积为8cm2?
(2)如果点P,Q同时出发,经过几秒钟时以P、C、Q为顶点的三角形与△ABC相似?
25.在△ABC中,AB=6,BC=5,AC=4,D是线段AB上一点,且DB=4,过点D作DE与线段AC相交于点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.请根据下列两位同学的交流回答问题:
(1)写出正确的比例式及后续解答;
(2)指出另一个错误,并给予正确解答.
26.如图,一块直角三角板的直角顶点P放在正方形ABCD的BC边上,并且使一条直角边经过点D,另一条直角边与AB交于点Q.请写出一对相似三角形,并加以证明.(图中不添加字母和线段)
27.在△ABC中,AD、CE分别是△ABC的两条高,且AD、CE相交于点O,试找出图中相似的三角形,并选出一组给出证明过程.
28.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从点A出发到点B止,动点E从点C出发到点A止.点D运动速度为1cm/s,点E运动速度为2cm/s.如果两个点同时运动,多长时间△ADE与△ABC相似?
29.如图,已知AD AC=AB AE,∠DAE=∠BAC.求证:△DAB∽△EAC.
30.如图,在平面直角坐标系中,点B(12,10),过点B作x轴的垂线,垂足为A.作y轴的垂线,垂足为C点D从O出发,沿y轴正方向以每秒1个单位长度运动;点E从O出发,沿x轴正方向以每秒3个单位长度运动;点F从B出发,沿BA方向以每秒2个单位长度运动.当E点运动到点A时,三点随之停止运动.设运动时间为t.
(1)用含t的代数式分别表示点E,点F的坐标.
(2)若△ODE与以点A,E,F为顶点的三角形相似,求t的值.
答案
一.选择题
C.C.C.C.C.B.B.A.C.C.A.
二.填空题
12.4或7或9.
13.2或.
14.EF∥BC或∠AFE=∠B或∠AEF=∠C.
15.∠C=∠E或∠BAC=∠DAE或∠BAD=∠CAE或.
16.∠P=∠B或∠Q=∠C或
17.∠ACP=∠B(或).
18.①④.
19.①②④⑤.
20.或.
21.3或.
22.2或3.
23.2或.
三.解答题
24.(1)设xs后,可使△PCQ的面积为8cm2.
由题意得,AP=xcm,PC=(6﹣x)cm,CQ=2xcm,
则(6﹣x) 2x=8,
整理得x2﹣6x+8=0,
解得x1=2,x2=4.
所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2.
(2)设t秒后以P、C、Q为顶点的三角形与△ABC相似,则PC=(6﹣t)cm,CQ=2tcm.
当△PCQ∽△ACB时,,即,
解得:t.
当△PCQ∽△BCA时,,即,
解得:t.
综上所述,当t秒或t秒时,以P、C、Q为顶点的三角形与△ABC相似.
25.解(1),
∴.
(2)另一个错在没有进行分类讨论,如图,过点D作∠ADE=∠ACB,
则△ADE∽△ACB,
∴,
∴.
综合以上可得,DE或.
26.△BPQ∽△CDP,
证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∵∠QPD=90°,
∴∠QPB+∠BQP=90°,
∠QPB+∠DPC=90°,
∴∠DPC=∠PQB,
∴△BPQ∽△CDP.
27.图中相似的三角形有:△ABD∽△CBE,△ODC∽△BEC,△OEA∽△BDA,△ODC∽△OEA.
∵AD、CE分别是△ABC的两条高,
∴∠ADB=∠CDA=∠CEB=∠AEC=90°,
∴∠B+∠BCE=90°,∠B+∠BAD=90°,
∴∠BAD=∠BCE,
∵∠EBC=∠ABD,
∴△ABD∽CBE.
28.如果两点同时运动,设运动t秒时,以点A、D、E为顶点的三角形与△ABC相似,
则AD=t,CE=2t,AE=AC﹣CE=12﹣2t.
①当D与B对应时,有△ADE∽△ABC.
∴AD:AB=AE:AC,
∴t:6=(12﹣2t):12,
∴t=3;
②当D与C对应时,有△ADE∽△ACB.
∴AD:AC=AE:AB,
∴t:12=(12﹣2t):6,
∴t=4.8.
所以当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是3秒或4.8秒.
29.证明:∵AD AC=AB AE,
∴,
∵∠DAE=∠BAC.
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠DAB=∠EAC,
∴△DAB∽△EAC.
30.(1)由题可得OE=3t,OD=t,BF=2t.
∵BA⊥x轴,BC⊥y轴,∠AOC=90°,
∴∠AOC=∠BAO=∠BCO=90°,
∴四边形OABC是矩形,
∴AB=OC,BC=OA.
∵B(12,10),
∴BC=OA=12,AB=OC=10,
∴AF=10﹣2t,AE=12﹣3t,
∴点E的坐标为(3t,0),点F的坐标为(12,10﹣2t);
(2)①当△ODE∽△AEF时,
则有,
∴,
解得t1=0(舍),t2;
②当△ODE∽△AFE时,
则有,
∴,
解得t1=0(舍),t2=6.
∵点E运动到点A时,三点随之停止运动,
∴3t≤12,
∴t≤4.
∵6>4,
∴t=6舍去,
综上所述:t的值为.
一.选择题
1. 如图.在△ABC中,DE∥BC,∠B=∠ACD,则图中相似三角形有( )
A.2对 B.3对 C.4对 D.5对
2. 如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与点A、C重合),DE与AB相交于点F,那么与△BFD相似的三角形是( )
A.△BFE B.△BDC C.△BDA D.△AFD
3. 如图,在Rt△ACB中,∠ACB=90°,AC=BC,点D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE,则图中与△ACE全等或相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
4. 如图,在△ABC中,∠B=70°,AB=4,BC=6,将△ABC沿图示中的虚线DE剪开,剪下的三角形与原三角形不相似的是( )
A. B.
C. D.
5.如图,在△ABC中,AB=AC=8,BC=6,点P从点B出发以1个单位/s的速度向点A运动,同时点Q从点C出发以2个单位/s的速度向点B运动.当以B,P,Q为顶点的三角形与△ABC相似时,运动时间为( )
A.s B.s C.s或s D.以上均不对
6. 已知△ABC是正三角形,点D是边AC上一动点(不与A、C重合),以BD为边作正△BDE,边DE与边AB交于点F,则图中一定相似的三角形有( )对.
A.6 B.5 C.4 D.3
7. 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则下列结论正确的有( )
①∠BAE=30°;②CE2=AB CF;③CFCD;④△ABE∽△AEF.
A.1个 B.2个 C.3个 D.4个
8. 如图,AD∥BC,∠D=90°,AD=3,BC=4,DC=6,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有( )
A.1 个 B.2 个 C.3 个 D.4 个
9. 坐标平面上横、纵坐标都为整数的点叫做整点.已知A(2,0),点B(3,1),O为坐标原点,在第一象限内取一整点C,使O,B,C三点所构成的三角形与△AOB相似.那么C点不同的位置一共有( )
A.1处 B.2处 C.3处 D.4处
10.如图,G,E分别是正方形ABCD的边AB,BC上的点,且AG=CE,AE⊥EF,AE=EF,如下结论:①BEGE;②△AGE≌△ECF;⑧∠FCD=45°;④△GBE∽△ECH,其中,正确的结论有( )
A.1个 B.2个 C.3个 D.4个
11.如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,对于下列结论:①AC=FG;②四边形CBFG是矩形;③△ACD∽△FEQ.其中正确的是( )
A.①②③ B.①② C.①③ D.②③
二.填空题
12.如图,Rt△ABC中,∠C=90°,∠B=60°,BC=4,D为BC的中点,E为AB上的动点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE与△ABC相似时,t的值为 .
13.如图,点P是边长为5的正方形ABCD内一点,且PB=2,PB⊥BF,垂足为点B,请在射线BF上找一点M,使得以B,M,C为顶点的三角形与△ABP相似,则BM= .
14.已知:△ABC中,点E是AB边的中点,点F在AC边上,要使△AEF与△ABC相似,则需要增加的一个条件是 .(写出一个即可)
15.如图,∠B=∠D,请你添加一个条件,使得△ABC∽△ADE,这个条件可以是 .
16.如图,在△ABC和△APQ中,∠PAB=∠QAC,若再增加一个条件就能使△APQ∽△ABC,则这个条件可以是 .
17.如图,点P是△ABC中AB边上的 点,请你添加 个条件使△ACP∽△ABC: .
18.如图,在边长为4的正方形ABCD中,点E、F分别是BC、CD的中点,DE、AF交于点G,AF的中点为H,连接BG、DH.给出下列结论:
①AF⊥DE;②DG;③HD∥BG;④△ABG∽△DHF.
其中正确的结论有 .(请填上所有正确结论的序号)
19.如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△A1B1C1,当C,B1,C1三点共线时,旋转角为α,连接BB1,交于AC于点D,下面结论:
①△AC1C为等腰三角形;②CA=CB1;③α=135°;④△AB1D∽△ACB1;⑤中,正确的结论的序号为 .
20.如图,在Rt△ABC中,∠C=90°,AB=5,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则BD的长为 .
21.如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P是线段AD上的动点,过P作PF⊥AE于F,当以点P、F、E为顶点的三角形与△ABE相似时,AP的长为 .
22.如图,四边形ABCD中,∠A=∠B=90°,AB=5cm,AD=3cm,BC=2cm,P是AB上一点,若以P、A、D为顶点的三角形与△PBC相似,则PA= cm.
23.如图,等腰△ABC中,AB=AC=5,BC=8,点F是边BC上不与点B,C重合的一个动点,直线DE垂直平分BF,垂足为D.当△ACF是直角三角形时,BD的长为 .
三.解答题
24.如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动,当其中一点到达终点时,另一点也随之停止运动.
(1)如果点P,Q同时出发,经过几秒钟时△PCQ的面积为8cm2?
(2)如果点P,Q同时出发,经过几秒钟时以P、C、Q为顶点的三角形与△ABC相似?
25.在△ABC中,AB=6,BC=5,AC=4,D是线段AB上一点,且DB=4,过点D作DE与线段AC相交于点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.请根据下列两位同学的交流回答问题:
(1)写出正确的比例式及后续解答;
(2)指出另一个错误,并给予正确解答.
26.如图,一块直角三角板的直角顶点P放在正方形ABCD的BC边上,并且使一条直角边经过点D,另一条直角边与AB交于点Q.请写出一对相似三角形,并加以证明.(图中不添加字母和线段)
27.在△ABC中,AD、CE分别是△ABC的两条高,且AD、CE相交于点O,试找出图中相似的三角形,并选出一组给出证明过程.
28.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从点A出发到点B止,动点E从点C出发到点A止.点D运动速度为1cm/s,点E运动速度为2cm/s.如果两个点同时运动,多长时间△ADE与△ABC相似?
29.如图,已知AD AC=AB AE,∠DAE=∠BAC.求证:△DAB∽△EAC.
30.如图,在平面直角坐标系中,点B(12,10),过点B作x轴的垂线,垂足为A.作y轴的垂线,垂足为C点D从O出发,沿y轴正方向以每秒1个单位长度运动;点E从O出发,沿x轴正方向以每秒3个单位长度运动;点F从B出发,沿BA方向以每秒2个单位长度运动.当E点运动到点A时,三点随之停止运动.设运动时间为t.
(1)用含t的代数式分别表示点E,点F的坐标.
(2)若△ODE与以点A,E,F为顶点的三角形相似,求t的值.
答案
一.选择题
C.C.C.C.C.B.B.A.C.C.A.
二.填空题
12.4或7或9.
13.2或.
14.EF∥BC或∠AFE=∠B或∠AEF=∠C.
15.∠C=∠E或∠BAC=∠DAE或∠BAD=∠CAE或.
16.∠P=∠B或∠Q=∠C或
17.∠ACP=∠B(或).
18.①④.
19.①②④⑤.
20.或.
21.3或.
22.2或3.
23.2或.
三.解答题
24.(1)设xs后,可使△PCQ的面积为8cm2.
由题意得,AP=xcm,PC=(6﹣x)cm,CQ=2xcm,
则(6﹣x) 2x=8,
整理得x2﹣6x+8=0,
解得x1=2,x2=4.
所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2.
(2)设t秒后以P、C、Q为顶点的三角形与△ABC相似,则PC=(6﹣t)cm,CQ=2tcm.
当△PCQ∽△ACB时,,即,
解得:t.
当△PCQ∽△BCA时,,即,
解得:t.
综上所述,当t秒或t秒时,以P、C、Q为顶点的三角形与△ABC相似.
25.解(1),
∴.
(2)另一个错在没有进行分类讨论,如图,过点D作∠ADE=∠ACB,
则△ADE∽△ACB,
∴,
∴.
综合以上可得,DE或.
26.△BPQ∽△CDP,
证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∵∠QPD=90°,
∴∠QPB+∠BQP=90°,
∠QPB+∠DPC=90°,
∴∠DPC=∠PQB,
∴△BPQ∽△CDP.
27.图中相似的三角形有:△ABD∽△CBE,△ODC∽△BEC,△OEA∽△BDA,△ODC∽△OEA.
∵AD、CE分别是△ABC的两条高,
∴∠ADB=∠CDA=∠CEB=∠AEC=90°,
∴∠B+∠BCE=90°,∠B+∠BAD=90°,
∴∠BAD=∠BCE,
∵∠EBC=∠ABD,
∴△ABD∽CBE.
28.如果两点同时运动,设运动t秒时,以点A、D、E为顶点的三角形与△ABC相似,
则AD=t,CE=2t,AE=AC﹣CE=12﹣2t.
①当D与B对应时,有△ADE∽△ABC.
∴AD:AB=AE:AC,
∴t:6=(12﹣2t):12,
∴t=3;
②当D与C对应时,有△ADE∽△ACB.
∴AD:AC=AE:AB,
∴t:12=(12﹣2t):6,
∴t=4.8.
所以当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是3秒或4.8秒.
29.证明:∵AD AC=AB AE,
∴,
∵∠DAE=∠BAC.
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
∴∠DAB=∠EAC,
∴△DAB∽△EAC.
30.(1)由题可得OE=3t,OD=t,BF=2t.
∵BA⊥x轴,BC⊥y轴,∠AOC=90°,
∴∠AOC=∠BAO=∠BCO=90°,
∴四边形OABC是矩形,
∴AB=OC,BC=OA.
∵B(12,10),
∴BC=OA=12,AB=OC=10,
∴AF=10﹣2t,AE=12﹣3t,
∴点E的坐标为(3t,0),点F的坐标为(12,10﹣2t);
(2)①当△ODE∽△AEF时,
则有,
∴,
解得t1=0(舍),t2;
②当△ODE∽△AFE时,
则有,
∴,
解得t1=0(舍),t2=6.
∵点E运动到点A时,三点随之停止运动,
∴3t≤12,
∴t≤4.
∵6>4,
∴t=6舍去,
综上所述:t的值为.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
