九年级数学下册试题 6.5相似三角形的性质同步练习-苏科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 6.5相似三角形的性质同步练习-苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 214.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 19:47:08 | ||
图片预览



文档简介
6.5相似三角形的性质
一.选择题
1. 在如图的正方形网格图中,A、B、C、D都是格点,AB、CD相交于点E,则CE:ED的比值为( )
A. B. C. D.
2. 如图,函数y(x<0)的图象经过Rt△ABO斜边OB的中点D,与直角边AB相交于C,连结AD.若AD=3,则△ABO的周长为( )
A.12 B.6 C.6+2 D.6+2
3. 如图,在平行四边形ABCD中,E是AB的中点,F是AD的中点,FE交AC于O点,交CB的延长线于G点,那么S△AOF:S△COG=( )
A.1:4 B.1:9 C.1:16 D.1:25
4. 在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC的周长之比为( )
A. B. C. D.
5. 如图,在 ABCD中,点E在DC边上,连接AE,交BD于点F,若DE:EC=3:2,则△DEF的面积与△BAF的面积之比为( )
A.3:5 B.9:4 C.9:25 D.3:2
6. 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=1,DB=3,则△ADE的面积与△ABC的面积的比等于( )
A. B. C. D.
7. 两个相似三角形面积比是4:9,其中一个三角形的周长为24cm,则另一个三角形的周长是( )cm.
A.16 B.16或28 C.36 D.16或36
8. 如图,E是矩形ABCD中AD边的中点,BE交AC于点F,△AEF的面积为2,则四边CDEF的面积为( )
A.6 B.8 C.10 D.12
9. 如图,在平行四边形ABCD中,点E是AB的中点,CE和BD交于点O,若S△EOB=1,则四边形AEOD的面积为( )
A.4 B.5 C.6 D.7
10.如图,在矩形ABCD中,E,F分别为边BC,CD的中点,线段AE,AF与对角线BD分别交于点G,H.设矩形ABCD的面积为S,则以下4个结论中:
①AG:GE=2:1;②BG:GH:HD=1:1:1;③S1+S2+S3S;④S2:S4:S6=1:2:4.
正确的结论有( )
A.1个 B.2个 C.3个 D.4个
11.在矩形ABCD中,AB=4,BC=2,E为BC中点,H,G分别是边AB,CD上的动点,且始终保持GH⊥AE,则EH+AG最小值为( )
A.2 B. C. D.1
12.如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:
①△APE≌△AME;
②PM+PN=AC;
③PE2+PF2=PO2;
④△POF∽△BNF;
⑤点O在M、N两点的连线上.
其中正确的是( )
A.①②③④ B.①②③⑤ C.①②③④⑤ D.③④⑤
二.填空题
13.如图所示,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为 .
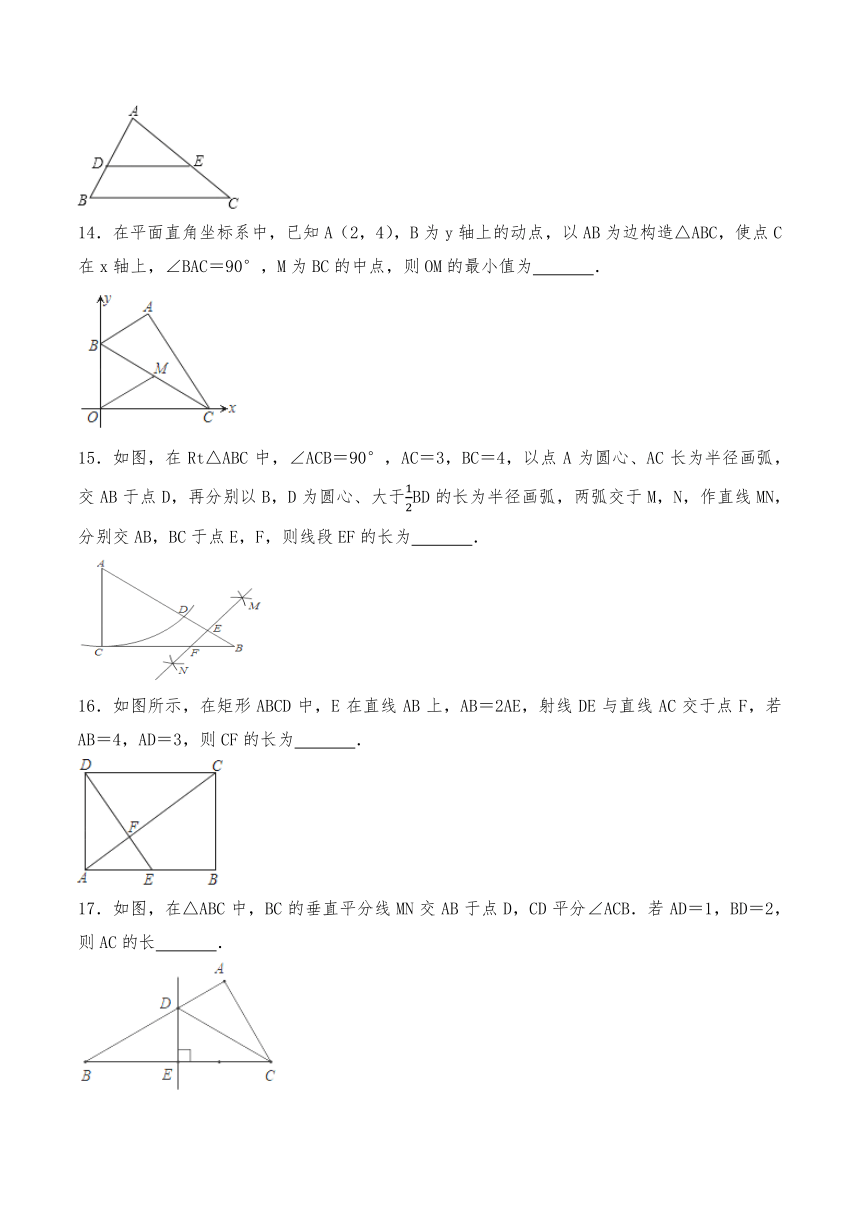
14.在平面直角坐标系中,已知A(2,4),B为y轴上的动点,以AB为边构造△ABC,使点C在x轴上,∠BAC=90°,M为BC的中点,则OM的最小值为 .
15.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心、AC长为半径画弧,交AB于点D,再分别以B,D为圆心、大于BD的长为半径画弧,两弧交于M,N,作直线MN,分别交AB,BC于点E,F,则线段EF的长为 .
16.如图所示,在矩形ABCD中,E在直线AB上,AB=2AE,射线DE与直线AC交于点F,若AB=4,AD=3,则CF的长为 .
17.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=1,BD=2,则AC的长 .
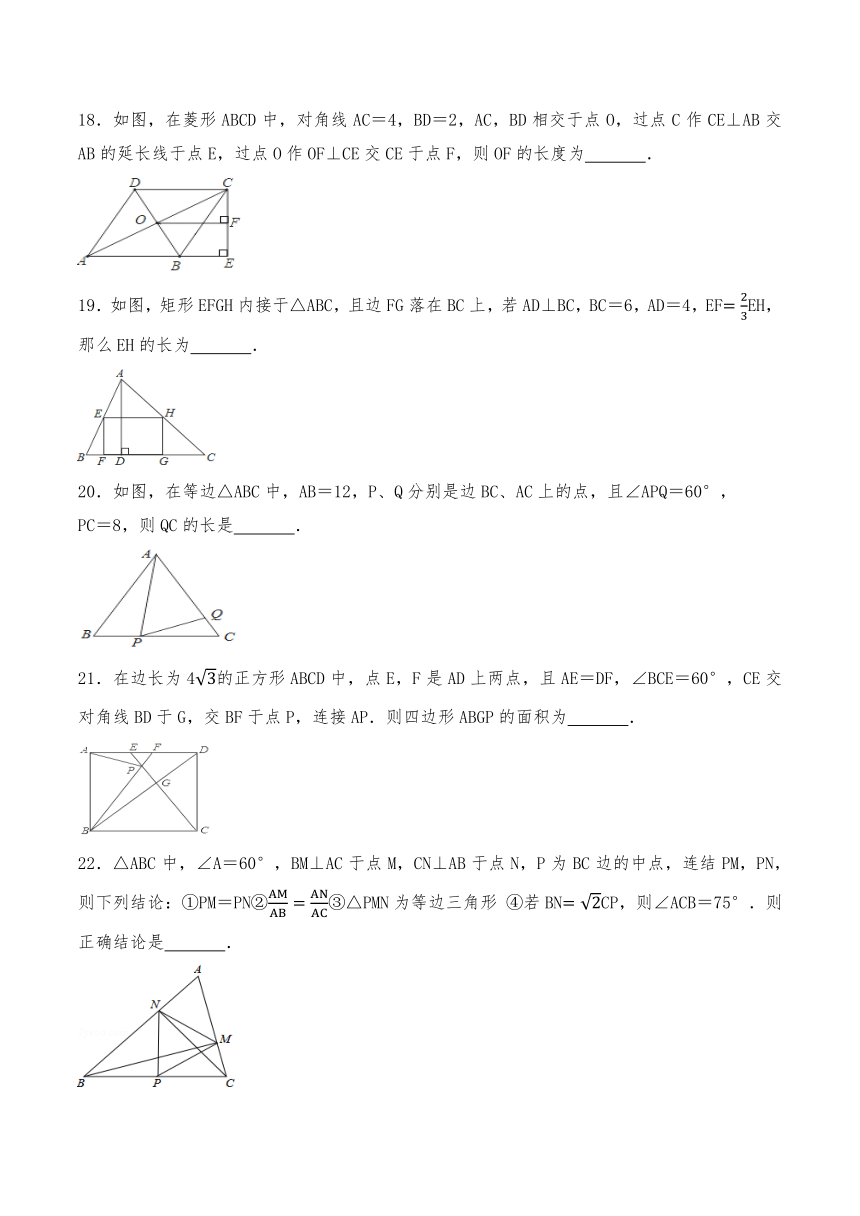
18.如图,在菱形ABCD中,对角线AC=4,BD=2,AC,BD相交于点O,过点C作CE⊥AB交AB的延长线于点E,过点O作OF⊥CE交CE于点F,则OF的长度为 .
19.如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=6,AD=4,EFEH,那么EH的长为 .
20.如图,在等边△ABC中,AB=12,P、Q分别是边BC、AC上的点,且∠APQ=60°,
PC=8,则QC的长是 .
21.在边长为4的正方形ABCD中,点E,F是AD上两点,且AE=DF,∠BCE=60°,CE交对角线BD于G,交BF于点P,连接AP.则四边形ABGP的面积为 .
22.△ABC中,∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连结PM,PN,则下列结论:①PM=PN②③△PMN为等边三角形 ④若BNCP,则∠ACB=75°.则正确结论是 .
三.解答题
23.如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为F.
(1)求证:△ADF∽△EAB;
(2)若DF=6,直接写出线段EF的长.
24.如图,已知在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD.
(2)若DE=6,BC=16,直接写出△FCD的面积.
25.如图,在正方形ABCD中,在BC边上取中点E,连接DE,过点E做EF⊥ED交AB于点G、交AD延长线于点F.
(1)求证:△ECD∽△DEF;
(2)若CD=4,求AF的长.
26.如图,在△ABC中,点E、F分别在AB、AC上,且.
(1)求证:△AEF∽△ABC;
(2)若点D在BC上,AD与EF交于点G,求证:.
27.请阅读下列材料,并完成相应任务
塞瓦定理
塞瓦定理载于1678年发表的《直线论》,是意大利数学家塞瓦的重大发现.如图,塞瓦定理是指在△ABC内任取一点O,延长AO,BO,CO分别交对边D,E,F于,则1.
任务:(1)当点D,E分别为边BC,AC的中点时,求证:点F为AB的中点;
(2)若△ABC为等边三角形,AB=12,AE=4,点D是BC边的中点,求BF的长.
28.如图,在△ABC中,BC=3,D为AC延长线上一点,AC=3CD,∠CBD=∠A,过D作DH∥AB,交BC的延长线于点H.
(1)求证:△HCD∽△HDB.
(2)求DH长度.
29.如图,△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点F,连接DE.
(1)求证:△ABD∽△ACE;
(2)求证:△ADE∽△ABC;
(3)若BE=CE,CD=1,求DF的长.
30.如图,在菱形ABCD中,∠ABC=60°,M为AD的中点,连接BM,交AC于E,在CB上取一点F,使得CF=AE,连接AF,交BM于G,连接CG.
(1)求∠BGF的度数;
(2)求的值;
(3)求证:BG⊥CG.
31.在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN.直线BD与MN相交于E.
(1)如图1,当点M在BC上时,求证:BD﹣2DEBM;
(2)如图2,当点M在BC延长线上时,连接BN交AD于点F.若DE,且AB:ND=1:2时,求线段BN的长.
答案
一.选择题
C.D.B.A.C.D.D.C.B.D.B.B.
二.填空题
13..
14..
15..
16.或10.
17..
18..
19.3.
20..
21.2424.
22.①②③④.
三.解答题
23.(1)证明:∵四边形ABCD为矩形,
∴∠B=90°,AD=BC=10,AD∥BC,
∵AD∥BC,
∴∠AEB=∠EAD,
∵DF⊥AE,
∴∠F=90°,
∵∠F=∠B,∠FAD=∠BEA,
∴△ADF∽△EAB;
(2)在Rt△ADF中,AF8,
∵△ADF∽△EAB,
∴,即,解得BE=4,
在Rt△ABE中,∵AB=3,BE=4,
∴AE5,
∴EF=AF﹣AE=8﹣5=3.
24.证明:∵AD=AC,
∴∠ADC=∠ACD,
∵D是BC的中点,ED⊥BC,
∴BE=EC,
∴∠ABC=∠ECD,
∴△ABC∽△FCD;
(2)如图,过点A作AH⊥BC于H,
∵BC=16,D是BC的中点,
∴CD=BD=8,
∵AD=AC,AH⊥CD,
∴DH=CH=4,
∴BH=12,
∵DE∥AH,
∴,
∴,
∴AH=9,
∵△ABC∽△FCD
∴()2,
∴S△FCDS△ABC=18.
25.(1)证明:∵四边形ABCD是正方形,EF⊥ED,
∴∠FED=∠C=90°,BC∥AD,
∴∠CED=∠FDE,
∴△ECD∽△DEF;
(2)∵四边形ABCD是正方形,
∴∠C=90°,AD=BC=CD=4,
∵E为BC的中点,
∴CEBC=2,
在Rt△DCE中,由勾股定理得:DE2,
∵△ECD∽△DEF,
∴,
∴,
解得:DF=10,
∵AD=4,
∴AF=DF﹣AD=10﹣4=6.
26.(1)证明:在△AEF和△ABC中,
,
∴△AEF∽△ABC;
(2)证明:∵△AEF∽△ABC,
∴∠AEF=∠ABC,
∴EF∥BC,
∴△AEG∽△ABD,△AGF∽△ADC,
∴,,
∴.
27.(1)证明:
∵D,E分别为边BC,AC的中点,
∴BD=CD,EA=CE,
∴,
由塞瓦定理,得,
∴,
∴AF=BF,
∴点F为AB的中点;
(2)∵△ABC为等边三角形,AB=12,
∴AB=AC=BC=12,
∵AE=4,
∴EC=12﹣4=8,
∵点D是BC的中点,
∴BD=CD=6,
∵AB=12,
∴AF=AB﹣BF=12﹣BF,
由赛瓦定理,得,
∴,
∴BF=8.
28.(1)证明:∵DH∥AB,
∴∠A=∠HDC,
∵∠CBD=∠A,
∴∠HDC=∠CBD,又∠H=∠H,
∴△HCD∽△HDB;
(2)∵DH∥AB,
∴,
∵AC=3CD,
∴,
∴CH=1,
∴BH=BC+CH=3+1=4,
由(1)知△HCD∽△HDB,
∴,
∴DH2=4×1=4,
∴DH=2(负值舍去).
答:DH的长度为2.
29.(1)证明;∵BD⊥AC于点D,CE⊥AB于点E,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ADB∽△AEC.
(2)证明:∵△ADB∽△AEC,
∴,
∴,
∵∠A=∠A,
∴△ADE∽△ABC.
(3)过点E作EN⊥ED交BD于N,过点E作EM⊥DN于M.
在Rt△BEC中,∵BE=EC,∠BEC=90°,
∴BCBE,∠BCF=45°,
∵∠BDC=90°,
∴BD3,
∵∠EFB=∠DFC,∠BEF=∠CDF=90°,
∴△BFE∽△CFD,
∴,
∴,
∵∠EFD=∠BFC,
∴△EFD∽△BFC,
∴∠EDF=∠BCF=45°,
∵∠NED=90°,
∴∠END=∠EDN=45°,
∴EN=ED,
∵∠BEC=∠NED=90°,
∴∠BEN=∠CED,
∵BE=CE,
∴△BEN≌△CED(SAS),
∴BN=CD=1,DN=BD﹣BN=2,
∵EN=ED,EM⊥DN,
∴MN=DM=1,
∴EM=MN=MD=1,
∵∠EMF=∠CDF=90°,∠EFM=∠CFD,EM=CD,
∴△EMF≌△CDF(AAS),
∴MF=DF,
∴DF.
30.(1)∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠ABC=∠ADC=60°,
∴△ABC,△ADC都是等边三角形,
∴AB=AC,∠BAE=∠ACF=60°,
∵AE=CF,
∴△BAE≌△ACF(SAS),
∴∠ABE=∠CAF,
∴∠BGF=∠ABE+∠BAG=∠CAF+∠BAG=∠BAC=60°.
(2)∵∠BAG+∠ABG=∠ABG+∠CBM=60°,
∴∠BAG=∠CBM,
∵AD∥CB,
∴∠AMB=∠CBM,
∴∠BAG=∠BMA,
∵∠ABG=∠ABM,
∴△BAG∽△BMA,
∴,
∴,
∵AM=MDADAB,
∴.
(3)设AM=DM=x,连接CM,
∵△ACD是等边三角形,
∴CM⊥AD,
∴CMAMx,
∵AD∥CB,
∴CM⊥BC,
∴∠BCM=90°,
∵AD=BC=2x,
∴BMx,
∵△BAG∽△BMA,
∴,
∴,
∴BGx,
∴,
∵∠CBG=∠CBM,
∴△CBG∽△MBC,
∴∠BGC=∠BCM=90°,
∴BG⊥CG.
31.(1)如图1,过点M作MF⊥BC交BD于点F,
∵四边形ABCD是正方形,
∴∠C=90°,
∴FM∥CD,
∴∠NDE=∠MFE,
∴FM=BM,
∵BM=DN,
∴FM=DN,
在△EFM和△EDN中,
,
∴△EFM≌△EDN(AAS),
∴EF=ED,
∴BD﹣2DE=BF,
根据勾股定理得:BFBM,
即BD﹣2DEBM;
(2)过点M作MF⊥BC交BD的延长线于点H,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴HM∥CD,
∴∠NDE=∠MHE,
∴HM=BM,
∵BM=DN,
∴HM=DN,
∵∠NED=∠MEH,
∴△EHM≌△EDN(AAS),
∴EH=ED,
∴BD+2DE=BH,
根据勾股定理得:BHBM,
即BD+2DEBM,
∴BDBC,
∵DE,
∴CM=2,
∵AB:ND=1:2,
∴CD:ND=1:2,
即CD:(CD+2)=1:2,
解得CD=2,
∴ND=4,
∴CN=CD+ND=6,
∴.
一.选择题
1. 在如图的正方形网格图中,A、B、C、D都是格点,AB、CD相交于点E,则CE:ED的比值为( )
A. B. C. D.
2. 如图,函数y(x<0)的图象经过Rt△ABO斜边OB的中点D,与直角边AB相交于C,连结AD.若AD=3,则△ABO的周长为( )
A.12 B.6 C.6+2 D.6+2
3. 如图,在平行四边形ABCD中,E是AB的中点,F是AD的中点,FE交AC于O点,交CB的延长线于G点,那么S△AOF:S△COG=( )
A.1:4 B.1:9 C.1:16 D.1:25
4. 在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC的周长之比为( )
A. B. C. D.
5. 如图,在 ABCD中,点E在DC边上,连接AE,交BD于点F,若DE:EC=3:2,则△DEF的面积与△BAF的面积之比为( )
A.3:5 B.9:4 C.9:25 D.3:2
6. 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=1,DB=3,则△ADE的面积与△ABC的面积的比等于( )
A. B. C. D.
7. 两个相似三角形面积比是4:9,其中一个三角形的周长为24cm,则另一个三角形的周长是( )cm.
A.16 B.16或28 C.36 D.16或36
8. 如图,E是矩形ABCD中AD边的中点,BE交AC于点F,△AEF的面积为2,则四边CDEF的面积为( )
A.6 B.8 C.10 D.12
9. 如图,在平行四边形ABCD中,点E是AB的中点,CE和BD交于点O,若S△EOB=1,则四边形AEOD的面积为( )
A.4 B.5 C.6 D.7
10.如图,在矩形ABCD中,E,F分别为边BC,CD的中点,线段AE,AF与对角线BD分别交于点G,H.设矩形ABCD的面积为S,则以下4个结论中:
①AG:GE=2:1;②BG:GH:HD=1:1:1;③S1+S2+S3S;④S2:S4:S6=1:2:4.
正确的结论有( )
A.1个 B.2个 C.3个 D.4个
11.在矩形ABCD中,AB=4,BC=2,E为BC中点,H,G分别是边AB,CD上的动点,且始终保持GH⊥AE,则EH+AG最小值为( )
A.2 B. C. D.1
12.如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:
①△APE≌△AME;
②PM+PN=AC;
③PE2+PF2=PO2;
④△POF∽△BNF;
⑤点O在M、N两点的连线上.
其中正确的是( )
A.①②③④ B.①②③⑤ C.①②③④⑤ D.③④⑤
二.填空题
13.如图所示,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为 .
14.在平面直角坐标系中,已知A(2,4),B为y轴上的动点,以AB为边构造△ABC,使点C在x轴上,∠BAC=90°,M为BC的中点,则OM的最小值为 .
15.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心、AC长为半径画弧,交AB于点D,再分别以B,D为圆心、大于BD的长为半径画弧,两弧交于M,N,作直线MN,分别交AB,BC于点E,F,则线段EF的长为 .
16.如图所示,在矩形ABCD中,E在直线AB上,AB=2AE,射线DE与直线AC交于点F,若AB=4,AD=3,则CF的长为 .
17.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=1,BD=2,则AC的长 .
18.如图,在菱形ABCD中,对角线AC=4,BD=2,AC,BD相交于点O,过点C作CE⊥AB交AB的延长线于点E,过点O作OF⊥CE交CE于点F,则OF的长度为 .
19.如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=6,AD=4,EFEH,那么EH的长为 .
20.如图,在等边△ABC中,AB=12,P、Q分别是边BC、AC上的点,且∠APQ=60°,
PC=8,则QC的长是 .
21.在边长为4的正方形ABCD中,点E,F是AD上两点,且AE=DF,∠BCE=60°,CE交对角线BD于G,交BF于点P,连接AP.则四边形ABGP的面积为 .
22.△ABC中,∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连结PM,PN,则下列结论:①PM=PN②③△PMN为等边三角形 ④若BNCP,则∠ACB=75°.则正确结论是 .
三.解答题
23.如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为F.
(1)求证:△ADF∽△EAB;
(2)若DF=6,直接写出线段EF的长.
24.如图,已知在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD.
(2)若DE=6,BC=16,直接写出△FCD的面积.
25.如图,在正方形ABCD中,在BC边上取中点E,连接DE,过点E做EF⊥ED交AB于点G、交AD延长线于点F.
(1)求证:△ECD∽△DEF;
(2)若CD=4,求AF的长.
26.如图,在△ABC中,点E、F分别在AB、AC上,且.
(1)求证:△AEF∽△ABC;
(2)若点D在BC上,AD与EF交于点G,求证:.
27.请阅读下列材料,并完成相应任务
塞瓦定理
塞瓦定理载于1678年发表的《直线论》,是意大利数学家塞瓦的重大发现.如图,塞瓦定理是指在△ABC内任取一点O,延长AO,BO,CO分别交对边D,E,F于,则1.
任务:(1)当点D,E分别为边BC,AC的中点时,求证:点F为AB的中点;
(2)若△ABC为等边三角形,AB=12,AE=4,点D是BC边的中点,求BF的长.
28.如图,在△ABC中,BC=3,D为AC延长线上一点,AC=3CD,∠CBD=∠A,过D作DH∥AB,交BC的延长线于点H.
(1)求证:△HCD∽△HDB.
(2)求DH长度.
29.如图,△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点F,连接DE.
(1)求证:△ABD∽△ACE;
(2)求证:△ADE∽△ABC;
(3)若BE=CE,CD=1,求DF的长.
30.如图,在菱形ABCD中,∠ABC=60°,M为AD的中点,连接BM,交AC于E,在CB上取一点F,使得CF=AE,连接AF,交BM于G,连接CG.
(1)求∠BGF的度数;
(2)求的值;
(3)求证:BG⊥CG.
31.在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN.直线BD与MN相交于E.
(1)如图1,当点M在BC上时,求证:BD﹣2DEBM;
(2)如图2,当点M在BC延长线上时,连接BN交AD于点F.若DE,且AB:ND=1:2时,求线段BN的长.
答案
一.选择题
C.D.B.A.C.D.D.C.B.D.B.B.
二.填空题
13..
14..
15..
16.或10.
17..
18..
19.3.
20..
21.2424.
22.①②③④.
三.解答题
23.(1)证明:∵四边形ABCD为矩形,
∴∠B=90°,AD=BC=10,AD∥BC,
∵AD∥BC,
∴∠AEB=∠EAD,
∵DF⊥AE,
∴∠F=90°,
∵∠F=∠B,∠FAD=∠BEA,
∴△ADF∽△EAB;
(2)在Rt△ADF中,AF8,
∵△ADF∽△EAB,
∴,即,解得BE=4,
在Rt△ABE中,∵AB=3,BE=4,
∴AE5,
∴EF=AF﹣AE=8﹣5=3.
24.证明:∵AD=AC,
∴∠ADC=∠ACD,
∵D是BC的中点,ED⊥BC,
∴BE=EC,
∴∠ABC=∠ECD,
∴△ABC∽△FCD;
(2)如图,过点A作AH⊥BC于H,
∵BC=16,D是BC的中点,
∴CD=BD=8,
∵AD=AC,AH⊥CD,
∴DH=CH=4,
∴BH=12,
∵DE∥AH,
∴,
∴,
∴AH=9,
∵△ABC∽△FCD
∴()2,
∴S△FCDS△ABC=18.
25.(1)证明:∵四边形ABCD是正方形,EF⊥ED,
∴∠FED=∠C=90°,BC∥AD,
∴∠CED=∠FDE,
∴△ECD∽△DEF;
(2)∵四边形ABCD是正方形,
∴∠C=90°,AD=BC=CD=4,
∵E为BC的中点,
∴CEBC=2,
在Rt△DCE中,由勾股定理得:DE2,
∵△ECD∽△DEF,
∴,
∴,
解得:DF=10,
∵AD=4,
∴AF=DF﹣AD=10﹣4=6.
26.(1)证明:在△AEF和△ABC中,
,
∴△AEF∽△ABC;
(2)证明:∵△AEF∽△ABC,
∴∠AEF=∠ABC,
∴EF∥BC,
∴△AEG∽△ABD,△AGF∽△ADC,
∴,,
∴.
27.(1)证明:
∵D,E分别为边BC,AC的中点,
∴BD=CD,EA=CE,
∴,
由塞瓦定理,得,
∴,
∴AF=BF,
∴点F为AB的中点;
(2)∵△ABC为等边三角形,AB=12,
∴AB=AC=BC=12,
∵AE=4,
∴EC=12﹣4=8,
∵点D是BC的中点,
∴BD=CD=6,
∵AB=12,
∴AF=AB﹣BF=12﹣BF,
由赛瓦定理,得,
∴,
∴BF=8.
28.(1)证明:∵DH∥AB,
∴∠A=∠HDC,
∵∠CBD=∠A,
∴∠HDC=∠CBD,又∠H=∠H,
∴△HCD∽△HDB;
(2)∵DH∥AB,
∴,
∵AC=3CD,
∴,
∴CH=1,
∴BH=BC+CH=3+1=4,
由(1)知△HCD∽△HDB,
∴,
∴DH2=4×1=4,
∴DH=2(负值舍去).
答:DH的长度为2.
29.(1)证明;∵BD⊥AC于点D,CE⊥AB于点E,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ADB∽△AEC.
(2)证明:∵△ADB∽△AEC,
∴,
∴,
∵∠A=∠A,
∴△ADE∽△ABC.
(3)过点E作EN⊥ED交BD于N,过点E作EM⊥DN于M.
在Rt△BEC中,∵BE=EC,∠BEC=90°,
∴BCBE,∠BCF=45°,
∵∠BDC=90°,
∴BD3,
∵∠EFB=∠DFC,∠BEF=∠CDF=90°,
∴△BFE∽△CFD,
∴,
∴,
∵∠EFD=∠BFC,
∴△EFD∽△BFC,
∴∠EDF=∠BCF=45°,
∵∠NED=90°,
∴∠END=∠EDN=45°,
∴EN=ED,
∵∠BEC=∠NED=90°,
∴∠BEN=∠CED,
∵BE=CE,
∴△BEN≌△CED(SAS),
∴BN=CD=1,DN=BD﹣BN=2,
∵EN=ED,EM⊥DN,
∴MN=DM=1,
∴EM=MN=MD=1,
∵∠EMF=∠CDF=90°,∠EFM=∠CFD,EM=CD,
∴△EMF≌△CDF(AAS),
∴MF=DF,
∴DF.
30.(1)∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠ABC=∠ADC=60°,
∴△ABC,△ADC都是等边三角形,
∴AB=AC,∠BAE=∠ACF=60°,
∵AE=CF,
∴△BAE≌△ACF(SAS),
∴∠ABE=∠CAF,
∴∠BGF=∠ABE+∠BAG=∠CAF+∠BAG=∠BAC=60°.
(2)∵∠BAG+∠ABG=∠ABG+∠CBM=60°,
∴∠BAG=∠CBM,
∵AD∥CB,
∴∠AMB=∠CBM,
∴∠BAG=∠BMA,
∵∠ABG=∠ABM,
∴△BAG∽△BMA,
∴,
∴,
∵AM=MDADAB,
∴.
(3)设AM=DM=x,连接CM,
∵△ACD是等边三角形,
∴CM⊥AD,
∴CMAMx,
∵AD∥CB,
∴CM⊥BC,
∴∠BCM=90°,
∵AD=BC=2x,
∴BMx,
∵△BAG∽△BMA,
∴,
∴,
∴BGx,
∴,
∵∠CBG=∠CBM,
∴△CBG∽△MBC,
∴∠BGC=∠BCM=90°,
∴BG⊥CG.
31.(1)如图1,过点M作MF⊥BC交BD于点F,
∵四边形ABCD是正方形,
∴∠C=90°,
∴FM∥CD,
∴∠NDE=∠MFE,
∴FM=BM,
∵BM=DN,
∴FM=DN,
在△EFM和△EDN中,
,
∴△EFM≌△EDN(AAS),
∴EF=ED,
∴BD﹣2DE=BF,
根据勾股定理得:BFBM,
即BD﹣2DEBM;
(2)过点M作MF⊥BC交BD的延长线于点H,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴HM∥CD,
∴∠NDE=∠MHE,
∴HM=BM,
∵BM=DN,
∴HM=DN,
∵∠NED=∠MEH,
∴△EHM≌△EDN(AAS),
∴EH=ED,
∴BD+2DE=BH,
根据勾股定理得:BHBM,
即BD+2DEBM,
∴BDBC,
∵DE,
∴CM=2,
∵AB:ND=1:2,
∴CD:ND=1:2,
即CD:(CD+2)=1:2,
解得CD=2,
∴ND=4,
∴CN=CD+ND=6,
∴.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
