人教版七年级数学上册 3.4实际问题与一元一次方程课件 (共67张PPT)
文档属性
| 名称 | 人教版七年级数学上册 3.4实际问题与一元一次方程课件 (共67张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 824.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 20:34:40 | ||
图片预览










文档简介
(共67张PPT)
第三章 一元一次方程
3.4实际问题与一元一次方程(1)
七年级数学·上 新课标 [人]
1.生活中存在着配套的问题,如图:
2.(1)在小学里我们学过有关工程问题的应用题,这类应用题中一般有工作总量、工作时间、工作效率这三个量.这三个量的关系是: ,
人们常规定工程问题中的工作总量为 .
工作总量=工作时间×工作效率
1
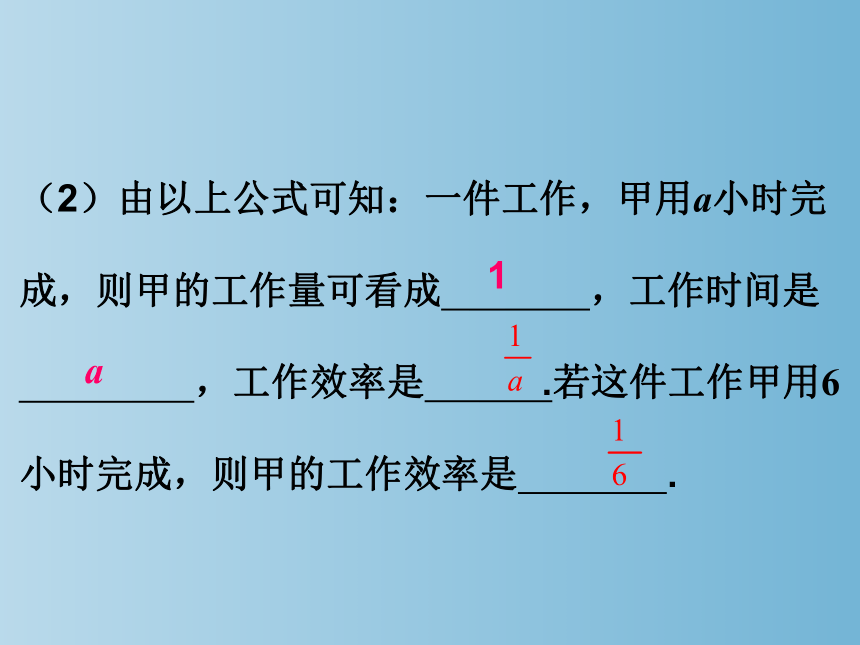
(2)由以上公式可知:一件工作,甲用a小时完成,则甲的工作量可看成 ,工作时间是 ,工作效率是 .若这件工作甲用6小时完成,则甲的工作效率是 .
1
a
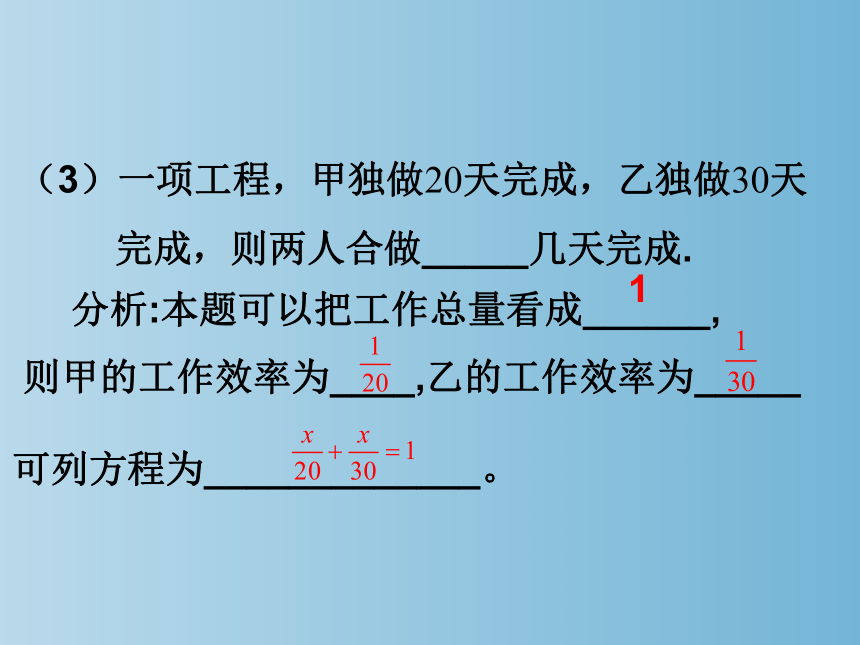
(3)一项工程,甲独做20天完成,乙独做30天
完成,则两人合做_____几天完成.
分析:本题可以把工作总量看成______,
则甲的工作效率为____,乙的工作效率为_____
可列方程为_____________。
1
分析:1.“1个螺钉要配2个螺母” 是什
么意思,包含着什么等量关系?
某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
螺母数量应是螺钉数量的2倍
2.本问题中有哪些等量关系?
生产螺母和生产螺钉的人数之和等于22,生产的螺母总数量应是螺钉总数量的2倍
解:
解:设应安排x名工人生产螺钉,(22-x)名工人
生产螺母.
2 000(22-x)=2 1200x
解得x=10 22- x=12
答:应安排10名工人生产螺钉,12名工人生产
螺母。
用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套.现在有36张白铁皮,用多少张制盒身,多少张制盒底,可使盒身与盒底正好配套?
解:设用x张白铁皮制盒身,(36-x)张制盒底,
则共制盒身25x个,共制盒底40(36-x)个,
2×25x=40(36-x)
解得x=16, 36-x=20
答:用16张制盒身,20张制盒底可使盒身与盒底正好配套。
包装厂有工人42人,每个工人平均每小时可以生产圆形铁片120片,或长方形铁片80片,两张圆形铁片与和一张长方形铁片可配套成一个圆桶,如何安排工人生产圆形或长方形铁片,使刚好配套?
解:设有工人x人生产圆形铁片,
120x=2 × 80(42-x)
答:有24人生产圆形铁片,18人生产长方形
铁片。
解得x=24, 42-x=18
整理一批图书,由一个人做要40 h完成.现计划由一部分人先做4h,然后增加2人与他们一起做8h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
1.人均效率为 .(指一个人1小时的工作量)
2.若设先由x人做4小时,完成的工作是 .再增加2人和前一部分人一起做8小时,两段完成的工作量之和是 .
解:
设安排x人先做4 h
解得 x=2
答:应安排2人先做4 h。
一项工程,甲单独做20天完成,乙单独做30天完成,若甲先单独做10天,剩下的部分由甲、乙合做,则还需几天完成?
解得x=6
答:还需要6天完成。
解:设还需要x天完成
小结
1.生产、调度、分配问题中的等量关系较隐蔽,要在弄清的基础上去解决.
2.对于工程问题,要注意:
(1)工作量=工作效率 工作时间.
(2)如果一件工作分几个阶段完成,那么各
阶段的工作量之和=总工作量.
(3)工作总量一般看作单位“1”。
1.某工程需动用15台挖土、运土机械,每台机械
每小时能挖土3 m3或运土2 m3,为了使得挖出
的土能及时运走,安排了x台机械挖土.则可列
方程为 ( )
A. 3x-2x=15 B.3x=2(15-x)
C.2x=3(15 -x) D.3x+2x=15
B
2.某班组每天需生产50个零件才能在规定时间内
完成一项生产任务,实际上该班组每天比计划
多生产6个零件,结果比规定时间提前3天并超额生产了120个零件,若设该班组需完成的零
件任务为x个,则可列方程为 ( )
C
A. B.
C. D.
3.某车间加工机轴和轴承,一个工人每天平均可
加工15个机轴或10个轴承,该车间共有80人,
一根机轴和两个轴承配成一套,则应分配多少
个工人加工机轴或轴承,才能使每天生产的机
轴和轴承正好配套?
解:设应分配x人加工机轴,则(80-x)人加工轴承。
2×15x=10(80-x)
解得x= 20
所以加工轴承的人数为80-x=80-20=60
答:应分配20人加工机轴,60人加工轴承,
才能使每天生产的机轴和轴承正好配套。
4.整理一批图书,由1人做160小时完成,先由一些人做4小时,再增加5人做6小时,完成这项工作的 ,则先安排了多少人做4小时?(假设这些人工作效率都相同)
解:设先安排x人做4小时
去括号,得4x+6x+30=120
移项及合并同类项,得10x=90
系数化为1,得x=9
答:先安排了9人做4小时。
第三章 一元一次方程
3.4实际问题与一元一次方程(2)
七年级数学·上 新课标 [人]
1.一支钢笔的进价是10元,利润是3元,这支钢
笔的售价为 元,利润率为 .
13
30%
进价+利润=售价
利润÷进价=利润率
①进价、售价、利润的关系
式: .
②进价、利润、利润率的关系
式: .
2.一件衬衣进价为100元,利润率为20%,这件衬
衣售价为 ______元.
120
(售价-进价)÷进价=利润率
③进价、售价、利润率的关系式: .
3.一个书包进价为60元,打八折销售后仍获利20元,这个书包的售价为 元,
原定价为_______元.
80
100
标价×折扣数=售价
标价=售价
标价、售价、折扣数的关系
式: ,
如果不打折,标价和售价的关系
式: .
一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,总的来说,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
盈利:售价>进价
利润=售价-进价>0
亏损:售价<进价
利润=售价-进价<0
解:设盈利25%的衣服的进价为x元
x+25%x=60
解得x=48
设亏损25%的衣服的进价为y元
y-25%y=60
解得y=80
两件衣服的进价和是x+y=128元,两件衣服的售价和120元.
因为进价>售价
所以卖这两件衣服亏损了8元.
(1)获利28元是怎么得来的
一件夹克衫先按成本提高50%标价,再以八折(标价的80%)出售,获利28元,这件夹克衫的成本是多少元
利润=售价-进价
50%x
(2)设商品成本是x元,商品的标价是 元,
商品售价是 元.
50%×80%×x
解:设商品的成本是x元
80%(1+50%)x-x=28
解得x=140
答:这件夹克衫的成本是140元。
商店对某种商品调价,按原价的八折出售,此时商品的利润率是10%,此商品的进价为1600元,商品的原价是多少元?
(1)原价是什么意思?
(2)设商品原价是x元,则商品的售价是 元?
(3)列方程为 ,
所以商品的原价是 元.
0.8x
0.8x-1600=1600 × 10%
2200
解:设商品的原价为x元
0.8x -1600=10%×1600
解得 x=220
答:商品的原价为220元
销售中盈亏问题中基本的量:
1.成本价:有时也称进价,是商家进货时的价格;
2.标价:商家在出售时,标注的价格;
3.售价:消费者购买时真正花的钱数;
4.商品利润=商品售价-商品成本价;
5.利润率:商品出售后利润与成本的比值;
销售问题中的几个等量关系:
①标价=进价×(1+利润率);
②利润与售价、进价的关系:利润=售价-进价;
③利润率与利润、进价的关系:
利润率=
④标价、实际售价与打折数的关系:
实际售价=标价×打折率
⑤实际售价与进价、利润之间的关系:
利润=实际售价-进价=标价×打折率-进价.
小结
1.商品经营中的盈利与亏损是生活中经常遇到
的问题,它不能 依靠直觉进行判断,必须依据
各个量之间的关系进行计算才能 得出正确结果.
2.销售中的盈亏问题,要掌握以下关系式:
(1)利润=售价-进价;
(2)利润率=
1.某商场购进一批服装,每件进价为200元,由
于换季滞销,商场决定将这种服装按标价的六
折销售,若打折后每件服装仍能获利20%,则该
服装的标价是( )
A.350元 B.400元 C.450元 D.500元
B
2.一件服装以120元销售,获利20%,则这件服装
的进价是( )
A.100元 B.105元 C.108元 D.118元
A
3.已知面包店的面包一个15元,小明去此店买面包,结账时店员告诉小明:“如果你再多买一个面包就可以打九折,价钱会比现在便宜45元”,小明说:“我买这些就好了,谢谢.”根据两人的对话,可知结账时小明买的面包数是( )
A.38 B.39 C.40 D.41
B
第三章 一元一次方程
3.4实际问题与一元一次方程(3)
七年级数学·上 新课标 [人]
比赛积分类问题
某次篮球联赛积分表:
解:设胜一场积x分,
从第一行得方程
10x+1×4=24
解得 x=2
用积分榜中其他行可以验证,
得出结论:负一场积1分,胜一场积2分
1.通过积分表,你能选择出其中哪一行最能说明
平一场积几分,负一场积几分吗?
意大利足球甲级联赛某赛季第26轮积分榜
解析:平场积分+负场积分=总积分
最后一行,平一场积1分,负一场积0分
2.你知道AC米兰队所积67分是怎样算出来的吗?
分析:胜场积分+平场积分=总积分
3.某队26场比赛中负的场次为10场,那么该队的胜场总积分等于它的平场总积分吗?
分析: ①平场数=比赛场数一胜场数.
②总积分=胜场积分+平场积分,
如果删去积分榜的最后一行,你还能用式子表示总积分与胜、负场数之间的数量关系吗?
例如:从第一、三行
设胜一场积x分,则前进队胜场积分为10x,负场积分为(24-10x)分
解得x=2
所以负一场积1分,胜一场积2分
列一元一次方程的表格法
将题目中的已知量和未知量及其关系填写在一张表内,使那些较为复杂的关系清晰明了地显示出来,从而能够较快地找出等量关系,列出方程。
某中学组织七年级学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车每日租金为每辆220元,60座客车每日租金为每辆300元
(1)七年级有多少人 原计划租用45座客车多少辆
(2)若租同一种车,要使每位同学都有座位,怎样租
用更合算
(1)设原计划租用45座客车x辆,
整理成下表:
45x+15=60(x-1)
45座客车 60座客车
每车人数(人) 45 60
租用辆数(辆) x x-1
学生总数(人) 45x+15 60(x-1)
(2)220×(5+1)=1320(元),300×(5-1)=1200(元).因为1320>1200,所以租用60座客车更合算.
解得x=5, 45x+15=240.
小结
1.积分多少与比赛的胜、负场次、积分规则有
关,弄清实际问题中所包含的数学问题是关键.
2.读懂题意,找出题中的等量关系是解决问题的
关键,能读懂表格,从表格中找到各量的关系
是解决这类问题的切入点.
3.用方程解决实际问题时,不仅要注意解方程的
过程是否正确,还要检验方程的解是否符合问
题的实际意义.
1.某球队参加了10场足球赛,共积17分,已知
胜一场得3分,平 一场得1分,负一场得O分,
其中该队输了3场,则该队胜的场次为 ( )
A.4 B.5 C.6 D.-7
B
2.在某次世界杯足球赛中,32支足球队被分成8
个小组进行单循环比赛,小组赛规则如下:胜一
场得3分,平一场得1分,负一场得O分.若小组中
某队的积分为5分,则该队必是( )
B
A.两胜一负 B.-胜两平
C.-胜一平一负 D.-胜两负
3.一份数学试卷共20道选择题,每答对一题得5分,不答或答错一题扣一分,一位同学得了82分,他答对了 道题.
17
4.足球比赛积分规则为:胜一场得3分,平一场得1分,负一场得﹣1分,某支球队打了14场,负两场, 得24分,这只球队胜了多少场?
解:设这只球队平了x场,则胜(14﹣2﹣x)场,
(14﹣2﹣x)×3+x+(﹣1)×2=24
解得 x=5. 14﹣2﹣5=7(场)
答:这只球队胜了7场.
第三章 一元一次方程
3.4实际问题与一元一次方(4)
七年级数学·上 新课标 [人]
问题(1)你了解表格中这些数字的意义吗?
问题(2)你觉得选择哪种计费方式更省钱呢?
月使用费/元 主叫限定时间/min 主叫超时费(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
问题(3)通过大家的讨论,你对电话计费问题有什么新的认识?
问题(4)设一个月内用移动电话主叫为tmin(t是正整数).当t在不同时间范围内取值时,列表说明按方式一和方式二如何计费,
问题(5) 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
结论:
(1)当t≤150时,方式一的计费少
(2)当t= 270时,两种计费方式相同
(3)当150(4)当270(5)当t=350时,方式二的计费少
(6)当t>350时,方式二的计费少
(1)当t<270 min时,选择方案一省钱
(2)当t>270 min时,选择方案二省钱
综上所述:
新华中学七(1)班准备外出进行野外考察活动,需要租用一辆大客车一天,现有甲、乙两辆客车的租用方案,甲车每天租金180元,另按实际行程每千米加收2元;乙车每天租金140元,另按实际行程每千米加收2.5元.
(1)当行程为多少千米时,两种方案的费用一样?
(2)若实际路程为100千米,为了节省费用,你认为租用哪辆车合算?
解:
(1)设行程为x千米时,两种方案的费用一样
180+2x=140+2.5x
答:当行程为80千米时,两种方案费用一样.
解得x= 80
(2)当行程为100千米时,
租甲车的费用为:180+2×100=380(元)
租乙车的费用为:140+2.5×100=390(元)
答:租甲车合算.
内容 类型 题中涉及的数量及公式 等量关系
注意事项
和差倍、分问题
由题可知
弄清“倍数”关系及“多、少”关系等.
等积变
形问题
各几何
体的体
积公式
变形前、
后的体
积相等
分清半
径、直径等
相遇
问题
路程=速度×时间
时间=路程/速度
速度=路程/时间
快者走的路
程+慢者走的
路程=原来
相距的路程
相向而行
注意始发
时间和地点
内容 类型 题中涉及的数量及公式 等量关系
注意事项
追及
问题
同向而行注意始发时间和地点
比例调
配问题
全部数量
=各部分
数量之和
把一份
设为x
工程
问题
工作量=工作效率×工
作时间
工作效率=工作总量/工作时间
工作时间=工作总量/工作效率
两个或多个工作
效率不同的对象
所完成的工作量
的和等于总工作
量
路程=速度×时间
时间=路程/速度
速度=路程/时间
快者走的路
程-慢者走的
路程=原来
相距的路程
一般情况下
把总工作量
看作1
内容 类型 题中涉及的数量及公式 等量关系
注意事项
利润率问题
打几折就是按原售价的百分之几十出售
利润率=
利润=售价-进价
找出利润或利润率之间的关系
内容 类型 题中涉及的数量及公式 等量关系
注意事项
数字问题
顺流航行速度=静水速度+水流速度
逆流航行速度=静水速度-水流速度
设a,b分别为
一个两位数的
个位数字与十
位数字,则这
个两位数可表
示为10b+a
一般情况下,设间接未知数
行船
问题
顺流航行速度 乘顺流航行时间=逆流航行速度 乘逆流航行时间
小结
解决优化方案问题的一般步骤:
1.运用一元一次方程解应用题的方法求解两种方案值相等的情况.
2.用特殊值试探法选择方案,取小于(或大于)一元一次方程解的值,比较两种方案的优劣后下结论.
1.某银行教育储蓄的年利率如下表:
小明现正读七年级,今年7月他父母为他在银行存款30000元,以供3年后上高中使用.要使3年后的收益最大,则小明的父母应该采用( )
一年期 二年期 三年期
2.25% 2.43% 2.70%
A.直接存一个三年期
B.先存一个一年期的,1年后将利息和自动转存一个两年期
C.先存一个一年期的,1年后将利息和自动转存两个一年期
D.先存一个两年期的,2年后将利息和自动转存一个一年期
C
2.某市家庭使用管道煤气收费标准为:每户每月煤气用量不超过60立方米,按每立方米0.8元收费;如果超过60立方米,超过部分按每立方米1.2元收费.已知小聪家12月份的煤气费为60元,则小聪家12月份的煤气用量为( )
A.49立方米 B.61立方米
C.70立方米 D.71立方米
C
3.国家为控制房价,出台新规“征收非唯一住宅二手房房产交易盈利部分的20%的个人所得税”,(房产交易盈利=实际成交价格﹣原购买价格)老王五年前购买了第二套房产,总价为60万,现想把这套房卖掉.除个人所得税外,还要缴纳契税、营业税及其他税.如下表:
房产面积 契税(占成交价) 营业税(占房产交易盈利) 其他税(占成交价)
不超过90m2 1% 0% 1%
不超过144m2 1.5% 0% 1%
超过144m2 3% 5.5% 1%
老王这套房子现在的市场价为7000元/m2.
(1)假设老王房子的面积是150m2,求老王共纳税多少万元?
解:7000×150=1050000(元)1050000元=105万元,105﹣60=45(万元)
45×(20%+5.5%)+105×(3%+1%)
答:老王共纳税15.675万元。
=45×0.255+105×0.04
=11.475+4.2=15.675(万元)
(2)老王这套房子实际共纳税100500元,求老王这套房子的面积有多大?
解:设老王这套房子的面积是x m2,实纳税款为y元,实际成交价格是0.7x万元,交易盈利为(0.7x﹣60)万元,
当0<x≤90时,
y=0.7x×(1%+1%)+(0.7x﹣60)×20%
=0.22×0.7x﹣12
≤0.22×0.7×90﹣12=1.86(万元)
当90<x≤144时,
y=0.7x×(1.5%+1%)+(0.7x﹣60)×20%
=0.225×0.7x﹣12≤0.225×0.7×144﹣12
=10.68(万元),且y>0.225×0.7×90-12=2.175(万元);
当x>144时,
y=0.7x×(3%+1%)+(0.7x﹣60)×(20%+5.5%)
=0.295×0.7x﹣15.3
>0.295×0.7×144﹣15.3
=14.436(万元)。
则老王这套房子的面积x应满足90<x≤144,
则0.225×0.7x﹣12=10.05,记得x=140.
答:老王这套房子的面积是140m
谢 谢 观 看
第三章 一元一次方程
3.4实际问题与一元一次方程(1)
七年级数学·上 新课标 [人]
1.生活中存在着配套的问题,如图:
2.(1)在小学里我们学过有关工程问题的应用题,这类应用题中一般有工作总量、工作时间、工作效率这三个量.这三个量的关系是: ,
人们常规定工程问题中的工作总量为 .
工作总量=工作时间×工作效率
1
(2)由以上公式可知:一件工作,甲用a小时完成,则甲的工作量可看成 ,工作时间是 ,工作效率是 .若这件工作甲用6小时完成,则甲的工作效率是 .
1
a
(3)一项工程,甲独做20天完成,乙独做30天
完成,则两人合做_____几天完成.
分析:本题可以把工作总量看成______,
则甲的工作效率为____,乙的工作效率为_____
可列方程为_____________。
1
分析:1.“1个螺钉要配2个螺母” 是什
么意思,包含着什么等量关系?
某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
螺母数量应是螺钉数量的2倍
2.本问题中有哪些等量关系?
生产螺母和生产螺钉的人数之和等于22,生产的螺母总数量应是螺钉总数量的2倍
解:
解:设应安排x名工人生产螺钉,(22-x)名工人
生产螺母.
2 000(22-x)=2 1200x
解得x=10 22- x=12
答:应安排10名工人生产螺钉,12名工人生产
螺母。
用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套.现在有36张白铁皮,用多少张制盒身,多少张制盒底,可使盒身与盒底正好配套?
解:设用x张白铁皮制盒身,(36-x)张制盒底,
则共制盒身25x个,共制盒底40(36-x)个,
2×25x=40(36-x)
解得x=16, 36-x=20
答:用16张制盒身,20张制盒底可使盒身与盒底正好配套。
包装厂有工人42人,每个工人平均每小时可以生产圆形铁片120片,或长方形铁片80片,两张圆形铁片与和一张长方形铁片可配套成一个圆桶,如何安排工人生产圆形或长方形铁片,使刚好配套?
解:设有工人x人生产圆形铁片,
120x=2 × 80(42-x)
答:有24人生产圆形铁片,18人生产长方形
铁片。
解得x=24, 42-x=18
整理一批图书,由一个人做要40 h完成.现计划由一部分人先做4h,然后增加2人与他们一起做8h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
1.人均效率为 .(指一个人1小时的工作量)
2.若设先由x人做4小时,完成的工作是 .再增加2人和前一部分人一起做8小时,两段完成的工作量之和是 .
解:
设安排x人先做4 h
解得 x=2
答:应安排2人先做4 h。
一项工程,甲单独做20天完成,乙单独做30天完成,若甲先单独做10天,剩下的部分由甲、乙合做,则还需几天完成?
解得x=6
答:还需要6天完成。
解:设还需要x天完成
小结
1.生产、调度、分配问题中的等量关系较隐蔽,要在弄清的基础上去解决.
2.对于工程问题,要注意:
(1)工作量=工作效率 工作时间.
(2)如果一件工作分几个阶段完成,那么各
阶段的工作量之和=总工作量.
(3)工作总量一般看作单位“1”。
1.某工程需动用15台挖土、运土机械,每台机械
每小时能挖土3 m3或运土2 m3,为了使得挖出
的土能及时运走,安排了x台机械挖土.则可列
方程为 ( )
A. 3x-2x=15 B.3x=2(15-x)
C.2x=3(15 -x) D.3x+2x=15
B
2.某班组每天需生产50个零件才能在规定时间内
完成一项生产任务,实际上该班组每天比计划
多生产6个零件,结果比规定时间提前3天并超额生产了120个零件,若设该班组需完成的零
件任务为x个,则可列方程为 ( )
C
A. B.
C. D.
3.某车间加工机轴和轴承,一个工人每天平均可
加工15个机轴或10个轴承,该车间共有80人,
一根机轴和两个轴承配成一套,则应分配多少
个工人加工机轴或轴承,才能使每天生产的机
轴和轴承正好配套?
解:设应分配x人加工机轴,则(80-x)人加工轴承。
2×15x=10(80-x)
解得x= 20
所以加工轴承的人数为80-x=80-20=60
答:应分配20人加工机轴,60人加工轴承,
才能使每天生产的机轴和轴承正好配套。
4.整理一批图书,由1人做160小时完成,先由一些人做4小时,再增加5人做6小时,完成这项工作的 ,则先安排了多少人做4小时?(假设这些人工作效率都相同)
解:设先安排x人做4小时
去括号,得4x+6x+30=120
移项及合并同类项,得10x=90
系数化为1,得x=9
答:先安排了9人做4小时。
第三章 一元一次方程
3.4实际问题与一元一次方程(2)
七年级数学·上 新课标 [人]
1.一支钢笔的进价是10元,利润是3元,这支钢
笔的售价为 元,利润率为 .
13
30%
进价+利润=售价
利润÷进价=利润率
①进价、售价、利润的关系
式: .
②进价、利润、利润率的关系
式: .
2.一件衬衣进价为100元,利润率为20%,这件衬
衣售价为 ______元.
120
(售价-进价)÷进价=利润率
③进价、售价、利润率的关系式: .
3.一个书包进价为60元,打八折销售后仍获利20元,这个书包的售价为 元,
原定价为_______元.
80
100
标价×折扣数=售价
标价=售价
标价、售价、折扣数的关系
式: ,
如果不打折,标价和售价的关系
式: .
一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,总的来说,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
盈利:售价>进价
利润=售价-进价>0
亏损:售价<进价
利润=售价-进价<0
解:设盈利25%的衣服的进价为x元
x+25%x=60
解得x=48
设亏损25%的衣服的进价为y元
y-25%y=60
解得y=80
两件衣服的进价和是x+y=128元,两件衣服的售价和120元.
因为进价>售价
所以卖这两件衣服亏损了8元.
(1)获利28元是怎么得来的
一件夹克衫先按成本提高50%标价,再以八折(标价的80%)出售,获利28元,这件夹克衫的成本是多少元
利润=售价-进价
50%x
(2)设商品成本是x元,商品的标价是 元,
商品售价是 元.
50%×80%×x
解:设商品的成本是x元
80%(1+50%)x-x=28
解得x=140
答:这件夹克衫的成本是140元。
商店对某种商品调价,按原价的八折出售,此时商品的利润率是10%,此商品的进价为1600元,商品的原价是多少元?
(1)原价是什么意思?
(2)设商品原价是x元,则商品的售价是 元?
(3)列方程为 ,
所以商品的原价是 元.
0.8x
0.8x-1600=1600 × 10%
2200
解:设商品的原价为x元
0.8x -1600=10%×1600
解得 x=220
答:商品的原价为220元
销售中盈亏问题中基本的量:
1.成本价:有时也称进价,是商家进货时的价格;
2.标价:商家在出售时,标注的价格;
3.售价:消费者购买时真正花的钱数;
4.商品利润=商品售价-商品成本价;
5.利润率:商品出售后利润与成本的比值;
销售问题中的几个等量关系:
①标价=进价×(1+利润率);
②利润与售价、进价的关系:利润=售价-进价;
③利润率与利润、进价的关系:
利润率=
④标价、实际售价与打折数的关系:
实际售价=标价×打折率
⑤实际售价与进价、利润之间的关系:
利润=实际售价-进价=标价×打折率-进价.
小结
1.商品经营中的盈利与亏损是生活中经常遇到
的问题,它不能 依靠直觉进行判断,必须依据
各个量之间的关系进行计算才能 得出正确结果.
2.销售中的盈亏问题,要掌握以下关系式:
(1)利润=售价-进价;
(2)利润率=
1.某商场购进一批服装,每件进价为200元,由
于换季滞销,商场决定将这种服装按标价的六
折销售,若打折后每件服装仍能获利20%,则该
服装的标价是( )
A.350元 B.400元 C.450元 D.500元
B
2.一件服装以120元销售,获利20%,则这件服装
的进价是( )
A.100元 B.105元 C.108元 D.118元
A
3.已知面包店的面包一个15元,小明去此店买面包,结账时店员告诉小明:“如果你再多买一个面包就可以打九折,价钱会比现在便宜45元”,小明说:“我买这些就好了,谢谢.”根据两人的对话,可知结账时小明买的面包数是( )
A.38 B.39 C.40 D.41
B
第三章 一元一次方程
3.4实际问题与一元一次方程(3)
七年级数学·上 新课标 [人]
比赛积分类问题
某次篮球联赛积分表:
解:设胜一场积x分,
从第一行得方程
10x+1×4=24
解得 x=2
用积分榜中其他行可以验证,
得出结论:负一场积1分,胜一场积2分
1.通过积分表,你能选择出其中哪一行最能说明
平一场积几分,负一场积几分吗?
意大利足球甲级联赛某赛季第26轮积分榜
解析:平场积分+负场积分=总积分
最后一行,平一场积1分,负一场积0分
2.你知道AC米兰队所积67分是怎样算出来的吗?
分析:胜场积分+平场积分=总积分
3.某队26场比赛中负的场次为10场,那么该队的胜场总积分等于它的平场总积分吗?
分析: ①平场数=比赛场数一胜场数.
②总积分=胜场积分+平场积分,
如果删去积分榜的最后一行,你还能用式子表示总积分与胜、负场数之间的数量关系吗?
例如:从第一、三行
设胜一场积x分,则前进队胜场积分为10x,负场积分为(24-10x)分
解得x=2
所以负一场积1分,胜一场积2分
列一元一次方程的表格法
将题目中的已知量和未知量及其关系填写在一张表内,使那些较为复杂的关系清晰明了地显示出来,从而能够较快地找出等量关系,列出方程。
某中学组织七年级学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车每日租金为每辆220元,60座客车每日租金为每辆300元
(1)七年级有多少人 原计划租用45座客车多少辆
(2)若租同一种车,要使每位同学都有座位,怎样租
用更合算
(1)设原计划租用45座客车x辆,
整理成下表:
45x+15=60(x-1)
45座客车 60座客车
每车人数(人) 45 60
租用辆数(辆) x x-1
学生总数(人) 45x+15 60(x-1)
(2)220×(5+1)=1320(元),300×(5-1)=1200(元).因为1320>1200,所以租用60座客车更合算.
解得x=5, 45x+15=240.
小结
1.积分多少与比赛的胜、负场次、积分规则有
关,弄清实际问题中所包含的数学问题是关键.
2.读懂题意,找出题中的等量关系是解决问题的
关键,能读懂表格,从表格中找到各量的关系
是解决这类问题的切入点.
3.用方程解决实际问题时,不仅要注意解方程的
过程是否正确,还要检验方程的解是否符合问
题的实际意义.
1.某球队参加了10场足球赛,共积17分,已知
胜一场得3分,平 一场得1分,负一场得O分,
其中该队输了3场,则该队胜的场次为 ( )
A.4 B.5 C.6 D.-7
B
2.在某次世界杯足球赛中,32支足球队被分成8
个小组进行单循环比赛,小组赛规则如下:胜一
场得3分,平一场得1分,负一场得O分.若小组中
某队的积分为5分,则该队必是( )
B
A.两胜一负 B.-胜两平
C.-胜一平一负 D.-胜两负
3.一份数学试卷共20道选择题,每答对一题得5分,不答或答错一题扣一分,一位同学得了82分,他答对了 道题.
17
4.足球比赛积分规则为:胜一场得3分,平一场得1分,负一场得﹣1分,某支球队打了14场,负两场, 得24分,这只球队胜了多少场?
解:设这只球队平了x场,则胜(14﹣2﹣x)场,
(14﹣2﹣x)×3+x+(﹣1)×2=24
解得 x=5. 14﹣2﹣5=7(场)
答:这只球队胜了7场.
第三章 一元一次方程
3.4实际问题与一元一次方(4)
七年级数学·上 新课标 [人]
问题(1)你了解表格中这些数字的意义吗?
问题(2)你觉得选择哪种计费方式更省钱呢?
月使用费/元 主叫限定时间/min 主叫超时费(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
问题(3)通过大家的讨论,你对电话计费问题有什么新的认识?
问题(4)设一个月内用移动电话主叫为tmin(t是正整数).当t在不同时间范围内取值时,列表说明按方式一和方式二如何计费,
问题(5) 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
结论:
(1)当t≤150时,方式一的计费少
(2)当t= 270时,两种计费方式相同
(3)当150
(6)当t>350时,方式二的计费少
(1)当t<270 min时,选择方案一省钱
(2)当t>270 min时,选择方案二省钱
综上所述:
新华中学七(1)班准备外出进行野外考察活动,需要租用一辆大客车一天,现有甲、乙两辆客车的租用方案,甲车每天租金180元,另按实际行程每千米加收2元;乙车每天租金140元,另按实际行程每千米加收2.5元.
(1)当行程为多少千米时,两种方案的费用一样?
(2)若实际路程为100千米,为了节省费用,你认为租用哪辆车合算?
解:
(1)设行程为x千米时,两种方案的费用一样
180+2x=140+2.5x
答:当行程为80千米时,两种方案费用一样.
解得x= 80
(2)当行程为100千米时,
租甲车的费用为:180+2×100=380(元)
租乙车的费用为:140+2.5×100=390(元)
答:租甲车合算.
内容 类型 题中涉及的数量及公式 等量关系
注意事项
和差倍、分问题
由题可知
弄清“倍数”关系及“多、少”关系等.
等积变
形问题
各几何
体的体
积公式
变形前、
后的体
积相等
分清半
径、直径等
相遇
问题
路程=速度×时间
时间=路程/速度
速度=路程/时间
快者走的路
程+慢者走的
路程=原来
相距的路程
相向而行
注意始发
时间和地点
内容 类型 题中涉及的数量及公式 等量关系
注意事项
追及
问题
同向而行注意始发时间和地点
比例调
配问题
全部数量
=各部分
数量之和
把一份
设为x
工程
问题
工作量=工作效率×工
作时间
工作效率=工作总量/工作时间
工作时间=工作总量/工作效率
两个或多个工作
效率不同的对象
所完成的工作量
的和等于总工作
量
路程=速度×时间
时间=路程/速度
速度=路程/时间
快者走的路
程-慢者走的
路程=原来
相距的路程
一般情况下
把总工作量
看作1
内容 类型 题中涉及的数量及公式 等量关系
注意事项
利润率问题
打几折就是按原售价的百分之几十出售
利润率=
利润=售价-进价
找出利润或利润率之间的关系
内容 类型 题中涉及的数量及公式 等量关系
注意事项
数字问题
顺流航行速度=静水速度+水流速度
逆流航行速度=静水速度-水流速度
设a,b分别为
一个两位数的
个位数字与十
位数字,则这
个两位数可表
示为10b+a
一般情况下,设间接未知数
行船
问题
顺流航行速度 乘顺流航行时间=逆流航行速度 乘逆流航行时间
小结
解决优化方案问题的一般步骤:
1.运用一元一次方程解应用题的方法求解两种方案值相等的情况.
2.用特殊值试探法选择方案,取小于(或大于)一元一次方程解的值,比较两种方案的优劣后下结论.
1.某银行教育储蓄的年利率如下表:
小明现正读七年级,今年7月他父母为他在银行存款30000元,以供3年后上高中使用.要使3年后的收益最大,则小明的父母应该采用( )
一年期 二年期 三年期
2.25% 2.43% 2.70%
A.直接存一个三年期
B.先存一个一年期的,1年后将利息和自动转存一个两年期
C.先存一个一年期的,1年后将利息和自动转存两个一年期
D.先存一个两年期的,2年后将利息和自动转存一个一年期
C
2.某市家庭使用管道煤气收费标准为:每户每月煤气用量不超过60立方米,按每立方米0.8元收费;如果超过60立方米,超过部分按每立方米1.2元收费.已知小聪家12月份的煤气费为60元,则小聪家12月份的煤气用量为( )
A.49立方米 B.61立方米
C.70立方米 D.71立方米
C
3.国家为控制房价,出台新规“征收非唯一住宅二手房房产交易盈利部分的20%的个人所得税”,(房产交易盈利=实际成交价格﹣原购买价格)老王五年前购买了第二套房产,总价为60万,现想把这套房卖掉.除个人所得税外,还要缴纳契税、营业税及其他税.如下表:
房产面积 契税(占成交价) 营业税(占房产交易盈利) 其他税(占成交价)
不超过90m2 1% 0% 1%
不超过144m2 1.5% 0% 1%
超过144m2 3% 5.5% 1%
老王这套房子现在的市场价为7000元/m2.
(1)假设老王房子的面积是150m2,求老王共纳税多少万元?
解:7000×150=1050000(元)1050000元=105万元,105﹣60=45(万元)
45×(20%+5.5%)+105×(3%+1%)
答:老王共纳税15.675万元。
=45×0.255+105×0.04
=11.475+4.2=15.675(万元)
(2)老王这套房子实际共纳税100500元,求老王这套房子的面积有多大?
解:设老王这套房子的面积是x m2,实纳税款为y元,实际成交价格是0.7x万元,交易盈利为(0.7x﹣60)万元,
当0<x≤90时,
y=0.7x×(1%+1%)+(0.7x﹣60)×20%
=0.22×0.7x﹣12
≤0.22×0.7×90﹣12=1.86(万元)
当90<x≤144时,
y=0.7x×(1.5%+1%)+(0.7x﹣60)×20%
=0.225×0.7x﹣12≤0.225×0.7×144﹣12
=10.68(万元),且y>0.225×0.7×90-12=2.175(万元);
当x>144时,
y=0.7x×(3%+1%)+(0.7x﹣60)×(20%+5.5%)
=0.295×0.7x﹣15.3
>0.295×0.7×144﹣15.3
=14.436(万元)。
则老王这套房子的面积x应满足90<x≤144,
则0.225×0.7x﹣12=10.05,记得x=140.
答:老王这套房子的面积是140m
谢 谢 观 看
