人教版七年级数学上册 3.3 解一元一次方程(二) ——去括号与去分母 课件 (共36张PPT)
文档属性
| 名称 | 人教版七年级数学上册 3.3 解一元一次方程(二) ——去括号与去分母 课件 (共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 398.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 20:35:35 | ||
图片预览











文档简介
(共36张PPT)
第三章 一元一次方程
3.3 解一元一次方程(二)
——去括号与去分母(1)
七年级数学·上 新课标 [人]
1.去括号。
(1)x-(x-4)
=x-x+4
(2) 8-2(x-7)
=8-2x+14
(3) 4(x+0.5)
=4x+2
2.解下列方程。
(1)x+4=2-x
解: x+x=2-4
2x=-2
x=-1
(2)3x=8+2x-6
解:3x-2x=8-6
x=2
解一元一次方程的基本步骤:
① 移项;
② 合并同类项;
③ 未知数的系数化为1.
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW·h(千瓦·时),全年用电15万kW·h.这个工厂去年上半年每月平均用电是多少?
设上半年每月平均用电x kW·h,则下半年每月平均用电_______ ,上半年共用电____,下半年共用电 , 全年共用
电_____________(用含有x的式子填空).
6x
6x+6(x-2000)
(x-2000)
6(x-2000)
解:
设上半年每月平均用电x kW·h.
去括号
移项
12x =162000
6x+6(x-2 000)=150 000
合并同类项
6x+6x-12000=150000
6x+6x =150000+12000
系数化为1
x=13500
去括号法则的依据是乘法分配律,以及有理数乘法的运算律. 去括号时注意用括号外面的数乘括号内的每一个数,同时注意每一个乘积的符号以及乘积的绝对值.
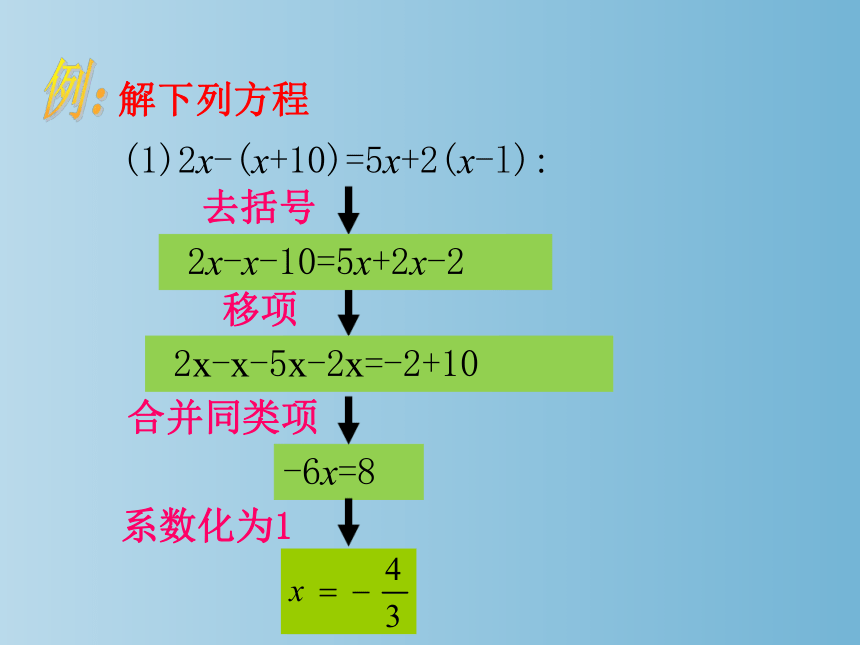
例:
解下列方程
去括号
移项
-6x=8
(1)2x-(x+10)=5x+2(x-l):
合并同类项
2x-x-10=5x+2x-2
2x-x-5x-2x=-2+10
系数化为1
例:
解下列方程
去括号
移项
5x=-3
(2)3x-7(x-l) =3-2(x+3)
合并同类项
3x-7+7=3-2x-6
3x+2x=3-7+7-6
系数化为1
一艘船从甲码头到乙码头顺流而行,用了
2 h;从乙码头返回甲码头逆流而行,用了
2.5 h,已知水流的速度是3 km/h,求船在静水中的平均速度.
1.行程问题中的基本关系式是什么?
路程=速度×时间
2.船在水中航行,它的速度都和哪些量有关,这些量之间的关系是怎样的?
顺水速度=静水速度+水流速度
逆水速度=静水速度-水流速度
3.题中等量关系是什么?
顺流速度×顺流时间=逆流速度×逆流时间
解:设船在静水中的速度为x km/h,则顺流速度
为(x+3)km/h,逆流速度为(x-3)km/h.
2(x+3)=2.5(x-3)
去括号,得2x+6=2.5x-7.5
移项及合并同类项,得 0.5x=13.5
系数化为1,得x=27
答:船在静水中的平均速度为27km/h。
小结
解方程实际上就是将一个复杂的方程,利用等式的性质和其他法则等逐步转化,最后变成 x=a的形式,其中x=a 既是方程,又是方程的解,去括号的主要理论依据是乘法分配律和有理数乘法法则.
1.对于方程2(2x-1) - ( -3)=1,去括号正确
的是( )
D
A.4x-1-x-3=1 B. 4x -1- x+3 =1
C.4x-2-x-3=1 D.4x-2-x+3=1
2.已知关于x的方程3x+2a=2的解是x=a-1,则a 的值为( )
A. 1 B. C. D.-1
A
3.解下列方程。
(1) 10-4(x+3) =2(x-1);
解:l0-4x-12=2x-2
-4x-2x=-2-10+12
x=0
-6x=0
3.解下列方程。
(2)2(y-3)-(4y-1)=6(1-y)
解: 2y-6-4y+1=6-6y
2y-4y+6y=6+6-1
4y=ll
4.毕业在即,九年级某班为纪念师生情谊,班委决定花800元班费买两种不同单价的留念册,分别给50位同学和10位任课老师每人一本留做纪念,其中送给任课老师的留念册的单价比给同学的单价多8元,请问这两种不同留念册的单价分别为多少元?
解:设送给任课老师的留念册的单价为x元,
10x+50( x-8)=800
解得x=20, x-8=12
答:送给任课老师的留念册的单价为20元,送给同学的留念册的单价为12元.
第三章 一元一次方程
3.3 解一元一次方程(二)
——去括号与去分母(2)
七年级数学·上 新课标 [人]
丢番图的墓志铭:“坟中安葬着丢番图,多么令人惊讶,它忠实地记录了所经历的道路.上帝给予的童年占六分之一,又过十二分之一,两颊长胡.再过七分之一,点燃起结婚的蜡烛.五年之后天赐贵子,可怜迟到的宁馨儿,享年仅及其父之半,便进入冰冷的墓.悲伤只有用数论的研究去弥补,又过四年,他也走完了人生的旅途.”请你列出方程算一算,丢番图去世时的年龄?
解一元一次方程的基本步骤:
①去括号,移项;
② 合并同类项;
③ 未知数的系数化为1.
一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.
解:设这个数是x,
解法2
左右两边乘42
97x =1386
合并同类项
28x+21x+6x+42x=1386
系数化为1
去分母
15x+5-20=3x-2-4x-6
去括号
5(3x+1)-10 ×2=(3x-2)-2(2x+3)
移项
16x=7
15x-3x+4x=-2-6-5+20
合并同类项
系数化为1
注意:
1.去分母时不要漏乘不含分母的项,
要注意分母线的括号作用.
2.去括号时要注意括号前的符号.
3.移项要变号.
方程中如果分子是一个多项式,去分母时要添加括号,变化为一个整数与一个括号乘积的形式,例如 ,去分母,即两边同乘12,得 在去分母时不可漏乘一些整数项或整式项,如
去分母,得 .
解方程
去分母,得
5(3x+1)-20=(3x-2)-2(2x+3)
去括号,得
15x+5-20=3x-2-4x-6
移项,得
15x-3x+4x= -2-6-5+20
合并同类项,得
16x=7
系数化为1,得
去分母解方程应注意:
(a)所选的乘数是方程中所有分母的最小公倍数,
不应遗漏;
(b)用各分母的最小公倍数乘方程的两边时,不要
遗漏方程中不含分母的项;
(c)去掉分母后,分数线也同时去掉,分子上的多
项式要用括号括起来.
归纳:
解下列方程
去分母,得
2(x+1)-4=8+(2-x)
去括号,得
2x+2-4=8+2-x
移项,得
2x+x=8+2-2+4
合并同类项,得
3x=12
系数化为1,得
去分母,得
18x+3( x-l)=18-2(2x-1)
去括号,得
18x+3x-3=18-4x+2
移项,得
18x+3x+4x=18+2+3
合并同类项,得
25x=23
系数化为1,得
小结
1.去分母解方程的过程中,两边必须同时乘各
分母的最小公倍数.
注意:①去分母时要注意分数线的括号作用.
②去分母时不要漏乘不含分母的项.
2.解一元一次方程的步骤:
①去分母;
②去括号;
③移项;
④合并同类项;
⑤系数化为1。
1.将方程 去分母时,方程两边应
同时乘( )
A.4 B.6 C.8 D.12
A
2.对于方程 ,变形第一步较好的 办法是( )
A.移项 B.去括号 C.去分母 D.合并同类项
C
3.某书中一道方程题 , 处印刷时被墨盖住了,查后面的答案,这道题的解为x=﹣2.5,那么 处的数为( )
A.﹣2.5 B.2.5 C.3.5 D.5
D
谢 谢 观 看
第三章 一元一次方程
3.3 解一元一次方程(二)
——去括号与去分母(1)
七年级数学·上 新课标 [人]
1.去括号。
(1)x-(x-4)
=x-x+4
(2) 8-2(x-7)
=8-2x+14
(3) 4(x+0.5)
=4x+2
2.解下列方程。
(1)x+4=2-x
解: x+x=2-4
2x=-2
x=-1
(2)3x=8+2x-6
解:3x-2x=8-6
x=2
解一元一次方程的基本步骤:
① 移项;
② 合并同类项;
③ 未知数的系数化为1.
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW·h(千瓦·时),全年用电15万kW·h.这个工厂去年上半年每月平均用电是多少?
设上半年每月平均用电x kW·h,则下半年每月平均用电_______ ,上半年共用电____,下半年共用电 , 全年共用
电_____________(用含有x的式子填空).
6x
6x+6(x-2000)
(x-2000)
6(x-2000)
解:
设上半年每月平均用电x kW·h.
去括号
移项
12x =162000
6x+6(x-2 000)=150 000
合并同类项
6x+6x-12000=150000
6x+6x =150000+12000
系数化为1
x=13500
去括号法则的依据是乘法分配律,以及有理数乘法的运算律. 去括号时注意用括号外面的数乘括号内的每一个数,同时注意每一个乘积的符号以及乘积的绝对值.
例:
解下列方程
去括号
移项
-6x=8
(1)2x-(x+10)=5x+2(x-l):
合并同类项
2x-x-10=5x+2x-2
2x-x-5x-2x=-2+10
系数化为1
例:
解下列方程
去括号
移项
5x=-3
(2)3x-7(x-l) =3-2(x+3)
合并同类项
3x-7+7=3-2x-6
3x+2x=3-7+7-6
系数化为1
一艘船从甲码头到乙码头顺流而行,用了
2 h;从乙码头返回甲码头逆流而行,用了
2.5 h,已知水流的速度是3 km/h,求船在静水中的平均速度.
1.行程问题中的基本关系式是什么?
路程=速度×时间
2.船在水中航行,它的速度都和哪些量有关,这些量之间的关系是怎样的?
顺水速度=静水速度+水流速度
逆水速度=静水速度-水流速度
3.题中等量关系是什么?
顺流速度×顺流时间=逆流速度×逆流时间
解:设船在静水中的速度为x km/h,则顺流速度
为(x+3)km/h,逆流速度为(x-3)km/h.
2(x+3)=2.5(x-3)
去括号,得2x+6=2.5x-7.5
移项及合并同类项,得 0.5x=13.5
系数化为1,得x=27
答:船在静水中的平均速度为27km/h。
小结
解方程实际上就是将一个复杂的方程,利用等式的性质和其他法则等逐步转化,最后变成 x=a的形式,其中x=a 既是方程,又是方程的解,去括号的主要理论依据是乘法分配律和有理数乘法法则.
1.对于方程2(2x-1) - ( -3)=1,去括号正确
的是( )
D
A.4x-1-x-3=1 B. 4x -1- x+3 =1
C.4x-2-x-3=1 D.4x-2-x+3=1
2.已知关于x的方程3x+2a=2的解是x=a-1,则a 的值为( )
A. 1 B. C. D.-1
A
3.解下列方程。
(1) 10-4(x+3) =2(x-1);
解:l0-4x-12=2x-2
-4x-2x=-2-10+12
x=0
-6x=0
3.解下列方程。
(2)2(y-3)-(4y-1)=6(1-y)
解: 2y-6-4y+1=6-6y
2y-4y+6y=6+6-1
4y=ll
4.毕业在即,九年级某班为纪念师生情谊,班委决定花800元班费买两种不同单价的留念册,分别给50位同学和10位任课老师每人一本留做纪念,其中送给任课老师的留念册的单价比给同学的单价多8元,请问这两种不同留念册的单价分别为多少元?
解:设送给任课老师的留念册的单价为x元,
10x+50( x-8)=800
解得x=20, x-8=12
答:送给任课老师的留念册的单价为20元,送给同学的留念册的单价为12元.
第三章 一元一次方程
3.3 解一元一次方程(二)
——去括号与去分母(2)
七年级数学·上 新课标 [人]
丢番图的墓志铭:“坟中安葬着丢番图,多么令人惊讶,它忠实地记录了所经历的道路.上帝给予的童年占六分之一,又过十二分之一,两颊长胡.再过七分之一,点燃起结婚的蜡烛.五年之后天赐贵子,可怜迟到的宁馨儿,享年仅及其父之半,便进入冰冷的墓.悲伤只有用数论的研究去弥补,又过四年,他也走完了人生的旅途.”请你列出方程算一算,丢番图去世时的年龄?
解一元一次方程的基本步骤:
①去括号,移项;
② 合并同类项;
③ 未知数的系数化为1.
一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.
解:设这个数是x,
解法2
左右两边乘42
97x =1386
合并同类项
28x+21x+6x+42x=1386
系数化为1
去分母
15x+5-20=3x-2-4x-6
去括号
5(3x+1)-10 ×2=(3x-2)-2(2x+3)
移项
16x=7
15x-3x+4x=-2-6-5+20
合并同类项
系数化为1
注意:
1.去分母时不要漏乘不含分母的项,
要注意分母线的括号作用.
2.去括号时要注意括号前的符号.
3.移项要变号.
方程中如果分子是一个多项式,去分母时要添加括号,变化为一个整数与一个括号乘积的形式,例如 ,去分母,即两边同乘12,得 在去分母时不可漏乘一些整数项或整式项,如
去分母,得 .
解方程
去分母,得
5(3x+1)-20=(3x-2)-2(2x+3)
去括号,得
15x+5-20=3x-2-4x-6
移项,得
15x-3x+4x= -2-6-5+20
合并同类项,得
16x=7
系数化为1,得
去分母解方程应注意:
(a)所选的乘数是方程中所有分母的最小公倍数,
不应遗漏;
(b)用各分母的最小公倍数乘方程的两边时,不要
遗漏方程中不含分母的项;
(c)去掉分母后,分数线也同时去掉,分子上的多
项式要用括号括起来.
归纳:
解下列方程
去分母,得
2(x+1)-4=8+(2-x)
去括号,得
2x+2-4=8+2-x
移项,得
2x+x=8+2-2+4
合并同类项,得
3x=12
系数化为1,得
去分母,得
18x+3( x-l)=18-2(2x-1)
去括号,得
18x+3x-3=18-4x+2
移项,得
18x+3x+4x=18+2+3
合并同类项,得
25x=23
系数化为1,得
小结
1.去分母解方程的过程中,两边必须同时乘各
分母的最小公倍数.
注意:①去分母时要注意分数线的括号作用.
②去分母时不要漏乘不含分母的项.
2.解一元一次方程的步骤:
①去分母;
②去括号;
③移项;
④合并同类项;
⑤系数化为1。
1.将方程 去分母时,方程两边应
同时乘( )
A.4 B.6 C.8 D.12
A
2.对于方程 ,变形第一步较好的 办法是( )
A.移项 B.去括号 C.去分母 D.合并同类项
C
3.某书中一道方程题 , 处印刷时被墨盖住了,查后面的答案,这道题的解为x=﹣2.5,那么 处的数为( )
A.﹣2.5 B.2.5 C.3.5 D.5
D
谢 谢 观 看
