人教版七年级数学上册 1.5.1乘方(1)课件 (共30张PPT)
文档属性
| 名称 | 人教版七年级数学上册 1.5.1乘方(1)课件 (共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 428.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
第一章 有理数
七年级数学·上 新课标 [人]
(1)求以下正方形的面积,边长如图所示.
2
——2 ×2=4
3
——3×3=9
a
——a×a=
(2)如图所示,正方体的棱长是3,体积是多少 若棱长是a呢
3
3
3
3×3×3=27
a×a×a=
(1)什么叫做乘方、幂、底数、指数
n个相同因数的积的运算叫乘方
乘方的结果叫幂
a叫做底数
n叫做指数
5
(2)怎样表示几个相同因数的积的运算
(3)当底数是负数或分数时应该怎样表示
(4) 的指数是多少
(1) 中,底数是 ,指数是 ,读作 .
3
2
2的3次幂
不一样,一个底数是-2,一个底数是2
2
8
1
(2) 中,底数是 ,指数是 ,读作 .
(3)8中的底数是 ,指数是 .
(4) 与 的意义一样吗 为什么
乘方的书写应注意:
小结
(1)n在a的右上方,书写时数字较小;
(2)一个数可以看作它本身的一次方,但指数
1通常省略不写;
(3)当a是分数或负数时,应用括号括起来,否
则一律理解为 底数是整数或正数。
计算。
=(-4)×(-4)×(-4)
=(-2)×(-2)×(-2)×(2)
=-64
=16
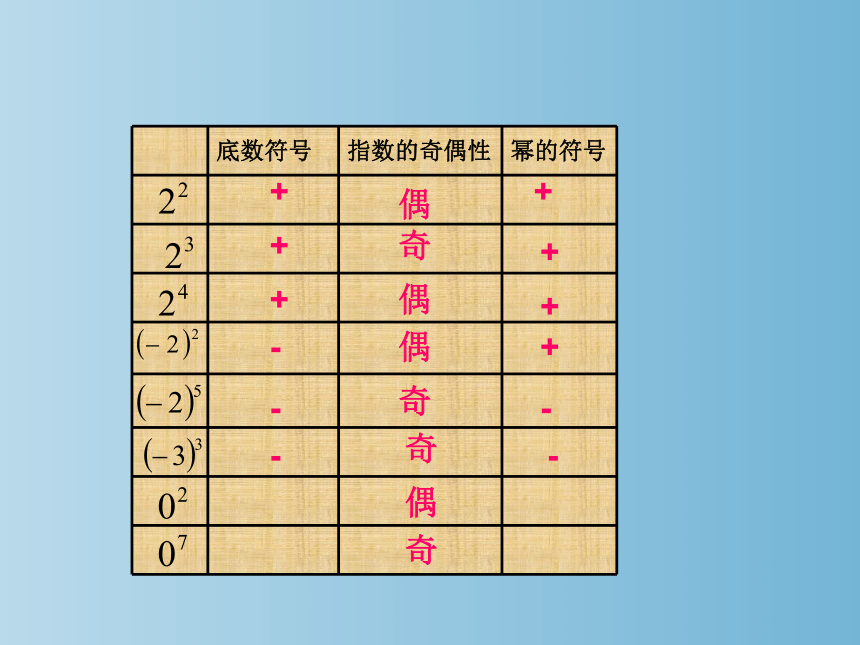
底数符号 指数的奇偶性 幂的符号
-
偶
+
+
奇
+
+
偶
+
-
偶
+
-
奇
-
+
奇
-
偶
奇
(1)任何数的偶次幂都是非负数.
(2)有理数的乘方运算与有理数的加、减、乘、除
运算一样,首先要确定结果的符号,然后再计算
结果的绝对值.
(3)由有理数的乘法法则可知:0的任何正整数次
幂都等于0,10的 几次幂等于1后面加几个0,1
的任何次幂都等于1.
用计算器计算 和 。
解:用带符号键 的计算器.
所以
显示结果为-32768.
显示结果为729
(-)
(-)
)
(
8
5
∧
=
(
(-)
3
)
∧
6
=
小结
有理数
的乘方
乘方的
法则
乘方的意义:n个相同因数的积的运算
正数的任何次幂都是正数
负数的奇次幂是负数
负数的偶次幂是正数
0的任何次幂都是0
1.计算﹣32 的结果是( )
A.9 B.-9 C.6 D.-6
B
2.下列各式:①-(-2);②-|-2|;③﹣22;④-(-2)2.
其中计算结果为负数的有( )
A.4个 B.3个 C.2个 D.1个
B
3.下列每对数中,不相等的一对是( )
A.(﹣2)3和﹣23 B. (﹣2)2和22
C. (﹣2)4和﹣24 D. |﹣2|3和|2|3
C
4.求下列各式的值.
第一章 有理数
1 . 5. 1 乘 方(2)
七年级数学·上 新课标 [人]
加减运算
乘方运算
乘除运算
混合
运算
有理数的运算级别:
小结
①先乘方,再乘除,最后加减;
②同级运算,从左到右进行;
级 别
名 称
第一级运算
加、减
第二级运算
乘、除
第三级
乘方(还有今后学的开方)
③如果有括号,先算括号内的运算,
按小括号、中括号、大括号依次进行.
下列计算有无错误?若有错,应该怎样改正?
(1)有理数的混合运算一般比较复杂,运算时
应时刻注意检查,并加强书写的规范性.注意
运算顺序和每一步运算的符号,并经常总结 经验教训.
小结
(2)一个算式中含有有理数的加、减、乘、除、
乘方等多种运算称为有理数的混合运算,在掌
握这几种基本运算的前提下,应首先注意运算
顺序.
(3)在进行混合运算时,除遵守上述原则外,
有时还需要注意灵活运用运算律,使运算准确又简便。
计算。
=-2×27+12+15
=-8-3×18+9÷2
=-27
=57.5
观察下面三行数:
-2, 4,-8, 16, -32, 64,…;①
0, 6,-6,18,-30,66,…;②
-1, 2,-4, 8,-16,32,….③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第10个数,计算这三个数的和.
(1)第①行数按什么规律排列?
列数等于 +2
列数等于 ÷2
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第10个数,计算这三个数的和.
小结
有理数的
混合运算
顺序
先乘方,再乘除,最后加减
同级运算,从左到右
( ) [ ] { }
小结
(1)减法运算转化为加法运算用相反数;
(2)除法运算转化为乘法运算用倒数;
(3)每一级运算都先确定符号再计算;
(4)能用运算律的,要用运算律简化计算.
方法:
1.算式17﹣2×[9﹣3×3×(﹣7)]÷3的值为
( )
A.-31 B. 0 C. 17 D.101
A
2.在算式21﹣(﹣ □24)的□中,可使计算出来的值是最小的运算符号是( )
A.+ B. - C. × D. ÷
B
2
3.计算.
谢 谢 观 看
第一章 有理数
七年级数学·上 新课标 [人]
(1)求以下正方形的面积,边长如图所示.
2
——2 ×2=4
3
——3×3=9
a
——a×a=
(2)如图所示,正方体的棱长是3,体积是多少 若棱长是a呢
3
3
3
3×3×3=27
a×a×a=
(1)什么叫做乘方、幂、底数、指数
n个相同因数的积的运算叫乘方
乘方的结果叫幂
a叫做底数
n叫做指数
5
(2)怎样表示几个相同因数的积的运算
(3)当底数是负数或分数时应该怎样表示
(4) 的指数是多少
(1) 中,底数是 ,指数是 ,读作 .
3
2
2的3次幂
不一样,一个底数是-2,一个底数是2
2
8
1
(2) 中,底数是 ,指数是 ,读作 .
(3)8中的底数是 ,指数是 .
(4) 与 的意义一样吗 为什么
乘方的书写应注意:
小结
(1)n在a的右上方,书写时数字较小;
(2)一个数可以看作它本身的一次方,但指数
1通常省略不写;
(3)当a是分数或负数时,应用括号括起来,否
则一律理解为 底数是整数或正数。
计算。
=(-4)×(-4)×(-4)
=(-2)×(-2)×(-2)×(2)
=-64
=16
底数符号 指数的奇偶性 幂的符号
-
偶
+
+
奇
+
+
偶
+
-
偶
+
-
奇
-
+
奇
-
偶
奇
(1)任何数的偶次幂都是非负数.
(2)有理数的乘方运算与有理数的加、减、乘、除
运算一样,首先要确定结果的符号,然后再计算
结果的绝对值.
(3)由有理数的乘法法则可知:0的任何正整数次
幂都等于0,10的 几次幂等于1后面加几个0,1
的任何次幂都等于1.
用计算器计算 和 。
解:用带符号键 的计算器.
所以
显示结果为-32768.
显示结果为729
(-)
(-)
)
(
8
5
∧
=
(
(-)
3
)
∧
6
=
小结
有理数
的乘方
乘方的
法则
乘方的意义:n个相同因数的积的运算
正数的任何次幂都是正数
负数的奇次幂是负数
负数的偶次幂是正数
0的任何次幂都是0
1.计算﹣32 的结果是( )
A.9 B.-9 C.6 D.-6
B
2.下列各式:①-(-2);②-|-2|;③﹣22;④-(-2)2.
其中计算结果为负数的有( )
A.4个 B.3个 C.2个 D.1个
B
3.下列每对数中,不相等的一对是( )
A.(﹣2)3和﹣23 B. (﹣2)2和22
C. (﹣2)4和﹣24 D. |﹣2|3和|2|3
C
4.求下列各式的值.
第一章 有理数
1 . 5. 1 乘 方(2)
七年级数学·上 新课标 [人]
加减运算
乘方运算
乘除运算
混合
运算
有理数的运算级别:
小结
①先乘方,再乘除,最后加减;
②同级运算,从左到右进行;
级 别
名 称
第一级运算
加、减
第二级运算
乘、除
第三级
乘方(还有今后学的开方)
③如果有括号,先算括号内的运算,
按小括号、中括号、大括号依次进行.
下列计算有无错误?若有错,应该怎样改正?
(1)有理数的混合运算一般比较复杂,运算时
应时刻注意检查,并加强书写的规范性.注意
运算顺序和每一步运算的符号,并经常总结 经验教训.
小结
(2)一个算式中含有有理数的加、减、乘、除、
乘方等多种运算称为有理数的混合运算,在掌
握这几种基本运算的前提下,应首先注意运算
顺序.
(3)在进行混合运算时,除遵守上述原则外,
有时还需要注意灵活运用运算律,使运算准确又简便。
计算。
=-2×27+12+15
=-8-3×18+9÷2
=-27
=57.5
观察下面三行数:
-2, 4,-8, 16, -32, 64,…;①
0, 6,-6,18,-30,66,…;②
-1, 2,-4, 8,-16,32,….③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第10个数,计算这三个数的和.
(1)第①行数按什么规律排列?
列数等于 +2
列数等于 ÷2
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第10个数,计算这三个数的和.
小结
有理数的
混合运算
顺序
先乘方,再乘除,最后加减
同级运算,从左到右
( ) [ ] { }
小结
(1)减法运算转化为加法运算用相反数;
(2)除法运算转化为乘法运算用倒数;
(3)每一级运算都先确定符号再计算;
(4)能用运算律的,要用运算律简化计算.
方法:
1.算式17﹣2×[9﹣3×3×(﹣7)]÷3的值为
( )
A.-31 B. 0 C. 17 D.101
A
2.在算式21﹣(﹣ □24)的□中,可使计算出来的值是最小的运算符号是( )
A.+ B. - C. × D. ÷
B
2
3.计算.
谢 谢 观 看
