2023-2024学年沪科版八年级数学上册期末复习综合检测试题(无答案)
文档属性
| 名称 | 2023-2024学年沪科版八年级数学上册期末复习综合检测试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 541.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 23:56:05 | ||
图片预览

文档简介
期末复习综合检测试题
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
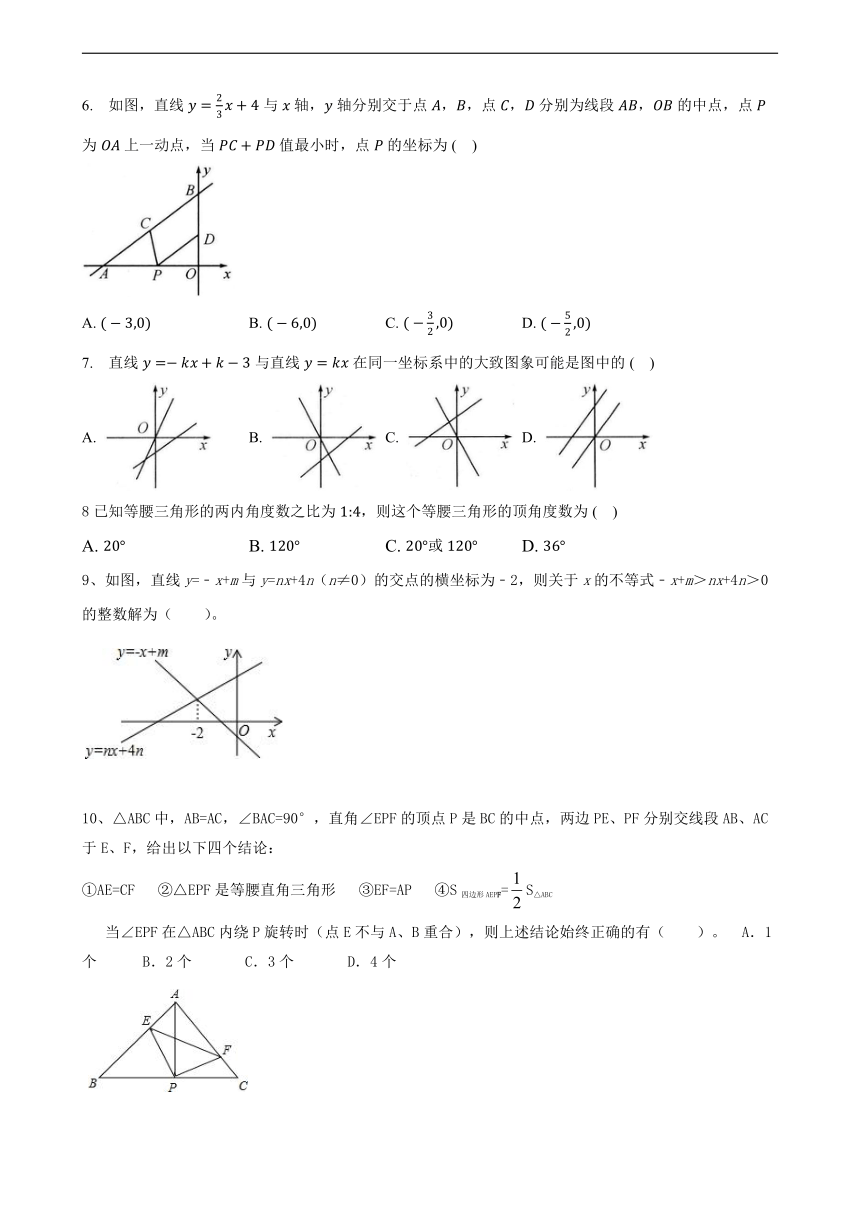
1下列图案中不是轴对称图形的是( )
A. B. C. D.
2.下列命题属于假命题的是( )
A.三个角对应相等的两个三角形全等
B.三边对应相等的两个三角形全等
C.全等三角形的对应边相等
D.全等三角形的面积相等
3.已知都在直线上,则的值的大小关系是( )
A. B. C. D.
4.下列所给条件中,能画出唯一的的是( )
A. B.
C. D.
5.当时,一次函数的图象大致是( )
A. B.
C. D.
6. 如图,直线与轴,轴分别交于点,,点,分别为线段,的中点,点为上一动点,当值最小时,点的坐标为( )
A. B. C. D.
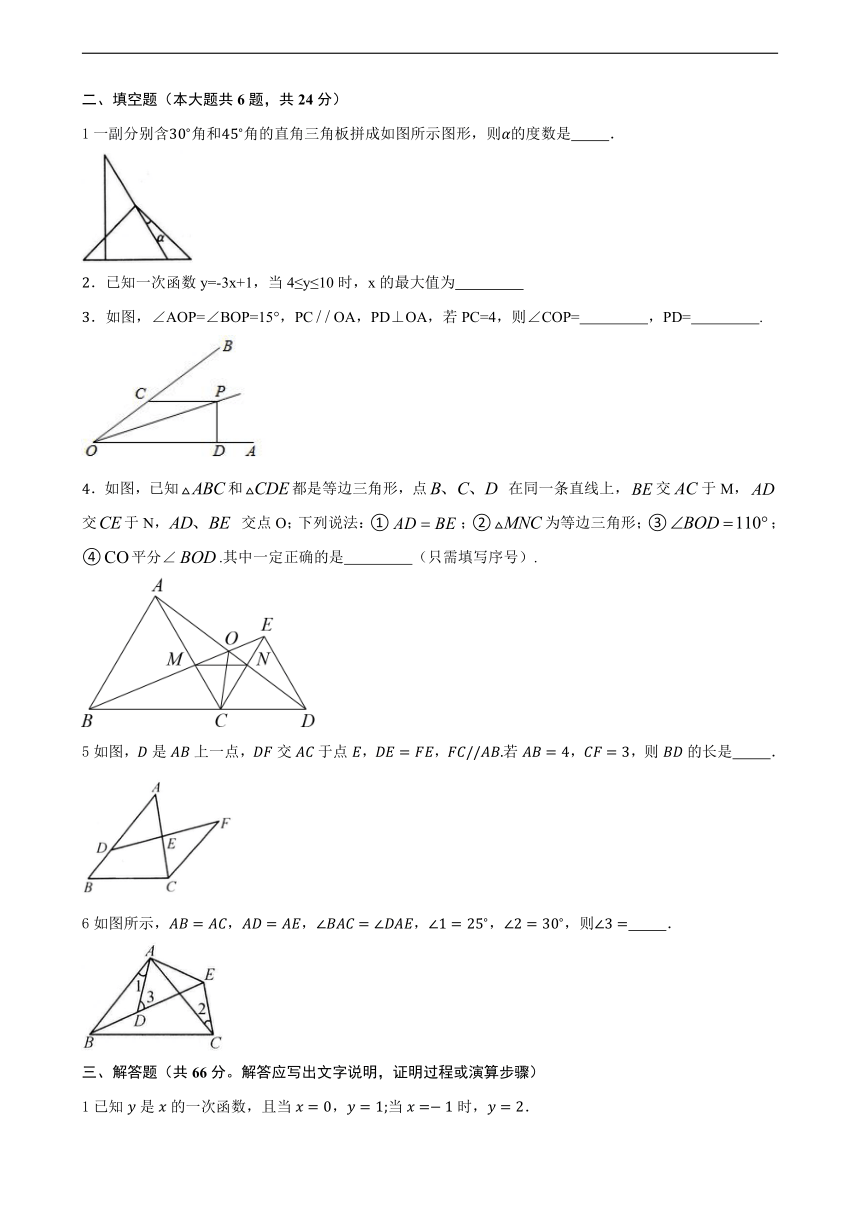
7. 直线与直线在同一坐标系中的大致图象可能是图中的( )
A. B. C. D.
8已知等腰三角形的两内角度数之比为,则这个等腰三角形的顶角度数为( )
A. B. C. 或 D.
9、如图,直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x+m>nx+4n>0的整数解为( )。
10、△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交线段AB、AC于E、F,给出以下四个结论:
①AE=CF ②△EPF是等腰直角三角形 ③EF=AP ④S四边形AEPF=S△ABC
当∠EPF在△ABC内绕P旋转时(点E不与A、B重合),则上述结论始终正确的有( )。 A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6题,共24分)
1一副分别含角和角的直角三角板拼成如图所示图形,则的度数是 .
2.已知一次函数y=-3x+1,当4≤y≤10时,x的最大值为
3.如图,∠AOP=∠BOP=15°,PCOA,PD⊥OA,若PC=4,则∠COP= ,PD= .
4.如图,已知和都是等边三角形,点 在同一条直线上,交于M,交于N, 交点O;下列说法:①;②为等边三角形;③;④平分∠.其中一定正确的是 (只需填写序号).
5如图,是上一点,交于点,,若,,则的长是 .
6如图所示,,,,,,则 .
三、解答题(共66分。解答应写出文字说明,证明过程或演算步骤)
1已知是的一次函数,且当,当时,.
求这个一次函数的表达式
将该函数图象向下平移个单位长度,求平移后图象的函数表达式.
2.如图,AB⊥AC,CD⊥BD,AB=DC,AC与BD交于点O.求证:OB=OC.
3. 中, , , 平分 交 于点D,求 的度数.
4.已知点P(a﹣1,3a+9),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P到x轴、y轴的距离相等且在第二象限.
5.如图,直线AD与BC交于点O,OA=OD,OB=OC,求证:△AOB≌△DOC.
6如图,已知两个一次函数和的图象交于点.
求点的坐标;
观察图象:当时,比较、的大小.
7如图,,,点,在上且.
求证:;
若平分,求证:.
8某通讯公司就手机流量套餐推出三种方案,如下表:
方案 方案 方案
每月基本费用元
每月免费使用流量兆 无限
超出后每兆收费元
,,三种方案每月所需的费用元与每月使用的流量兆之间的函数关系如图所示.
请直接写出,的值.
在方案中,当每月使用的流量不少于兆时,求每月所需的费用元与每月使用的流量兆之间的函数关系式.
在这三种方案中,当每月使用的流理超过多少兆时,选择方案最划算?
9.观察与发现:
小明将三角形纸片沿过点的直线折叠,使得落在边上,折痕为展开纸片如图再次折叠该三角形纸片,使点和点重合,折痕为,与相交于点,展平纸片后得到如图小明认为是等腰三角形,你同意吗请说明理由.
实践与运用:
将长方形纸片沿过点的直线折叠,使点落在边上的点处,折痕为如图再沿过点的直线折叠,使点落在上的点处,折痕为如图再展平纸片如图,求图中的大小.
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1下列图案中不是轴对称图形的是( )
A. B. C. D.
2.下列命题属于假命题的是( )
A.三个角对应相等的两个三角形全等
B.三边对应相等的两个三角形全等
C.全等三角形的对应边相等
D.全等三角形的面积相等
3.已知都在直线上,则的值的大小关系是( )
A. B. C. D.
4.下列所给条件中,能画出唯一的的是( )
A. B.
C. D.
5.当时,一次函数的图象大致是( )
A. B.
C. D.
6. 如图,直线与轴,轴分别交于点,,点,分别为线段,的中点,点为上一动点,当值最小时,点的坐标为( )
A. B. C. D.
7. 直线与直线在同一坐标系中的大致图象可能是图中的( )
A. B. C. D.
8已知等腰三角形的两内角度数之比为,则这个等腰三角形的顶角度数为( )
A. B. C. 或 D.
9、如图,直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x+m>nx+4n>0的整数解为( )。
10、△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交线段AB、AC于E、F,给出以下四个结论:
①AE=CF ②△EPF是等腰直角三角形 ③EF=AP ④S四边形AEPF=S△ABC
当∠EPF在△ABC内绕P旋转时(点E不与A、B重合),则上述结论始终正确的有( )。 A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6题,共24分)
1一副分别含角和角的直角三角板拼成如图所示图形,则的度数是 .
2.已知一次函数y=-3x+1,当4≤y≤10时,x的最大值为
3.如图,∠AOP=∠BOP=15°,PCOA,PD⊥OA,若PC=4,则∠COP= ,PD= .
4.如图,已知和都是等边三角形,点 在同一条直线上,交于M,交于N, 交点O;下列说法:①;②为等边三角形;③;④平分∠.其中一定正确的是 (只需填写序号).
5如图,是上一点,交于点,,若,,则的长是 .
6如图所示,,,,,,则 .
三、解答题(共66分。解答应写出文字说明,证明过程或演算步骤)
1已知是的一次函数,且当,当时,.
求这个一次函数的表达式
将该函数图象向下平移个单位长度,求平移后图象的函数表达式.
2.如图,AB⊥AC,CD⊥BD,AB=DC,AC与BD交于点O.求证:OB=OC.
3. 中, , , 平分 交 于点D,求 的度数.
4.已知点P(a﹣1,3a+9),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P到x轴、y轴的距离相等且在第二象限.
5.如图,直线AD与BC交于点O,OA=OD,OB=OC,求证:△AOB≌△DOC.
6如图,已知两个一次函数和的图象交于点.
求点的坐标;
观察图象:当时,比较、的大小.
7如图,,,点,在上且.
求证:;
若平分,求证:.
8某通讯公司就手机流量套餐推出三种方案,如下表:
方案 方案 方案
每月基本费用元
每月免费使用流量兆 无限
超出后每兆收费元
,,三种方案每月所需的费用元与每月使用的流量兆之间的函数关系如图所示.
请直接写出,的值.
在方案中,当每月使用的流量不少于兆时,求每月所需的费用元与每月使用的流量兆之间的函数关系式.
在这三种方案中,当每月使用的流理超过多少兆时,选择方案最划算?
9.观察与发现:
小明将三角形纸片沿过点的直线折叠,使得落在边上,折痕为展开纸片如图再次折叠该三角形纸片,使点和点重合,折痕为,与相交于点,展平纸片后得到如图小明认为是等腰三角形,你同意吗请说明理由.
实践与运用:
将长方形纸片沿过点的直线折叠,使点落在边上的点处,折痕为如图再沿过点的直线折叠,使点落在上的点处,折痕为如图再展平纸片如图,求图中的大小.
同课章节目录
