9.5三角形的中位线课件

课件48张PPT。§9.5 三角形的中位线
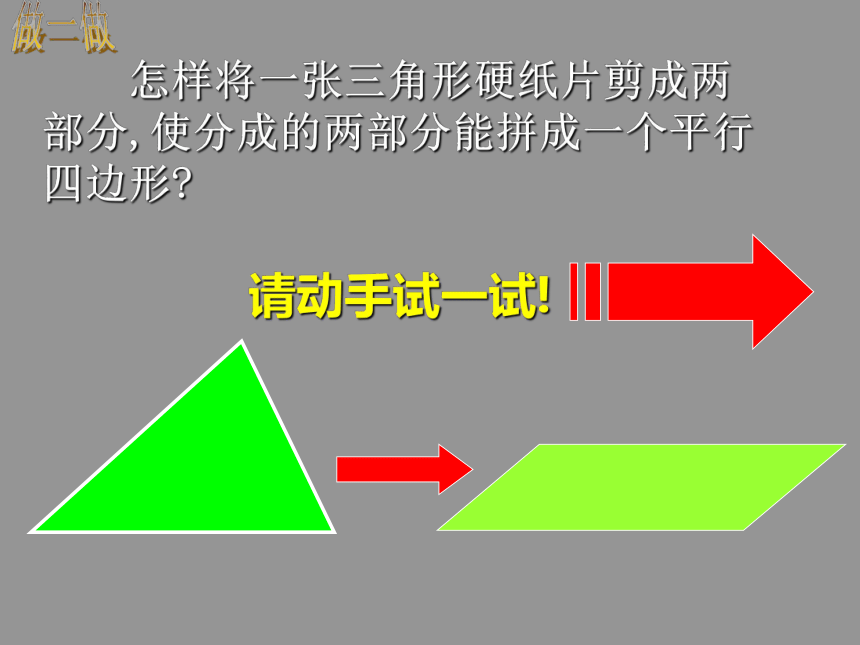
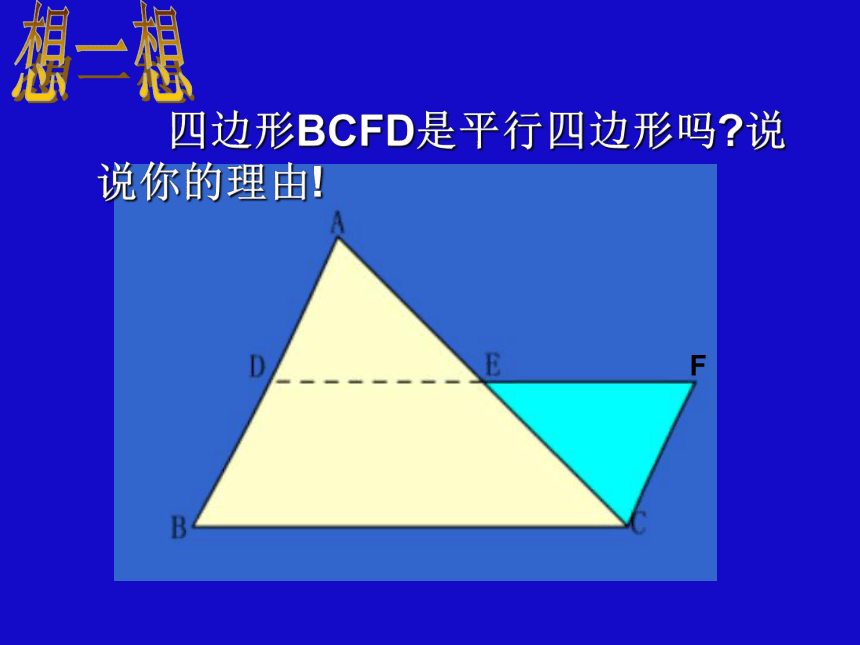
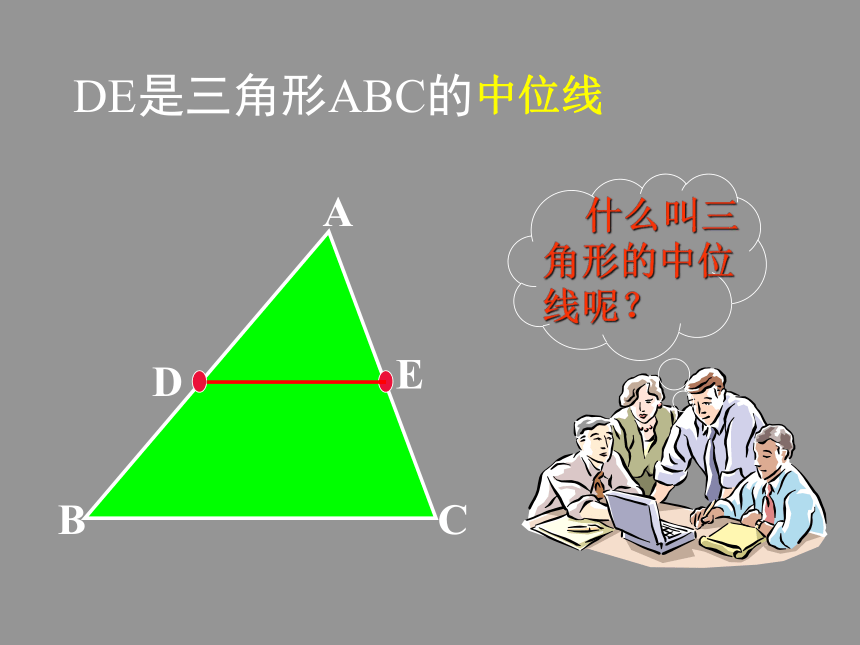
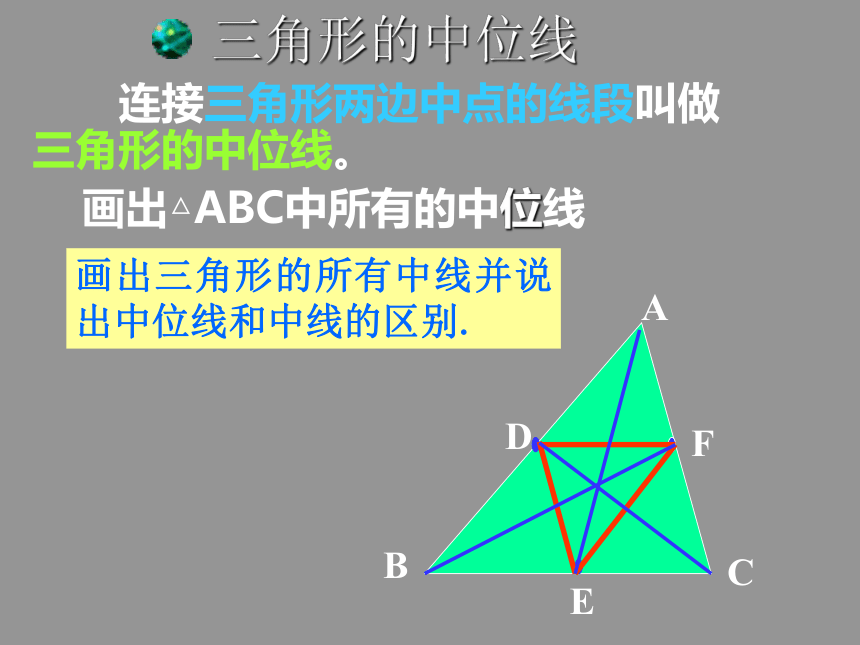
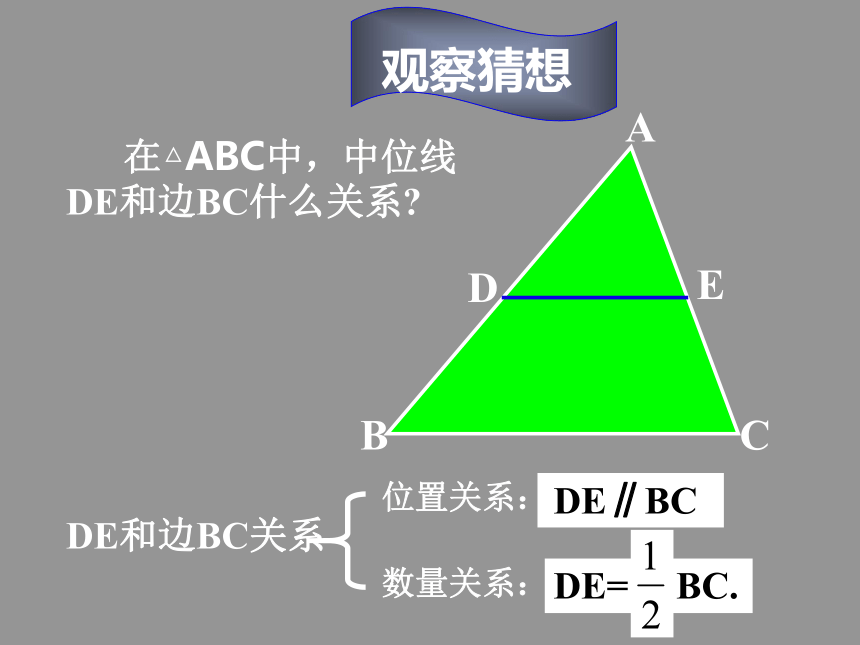
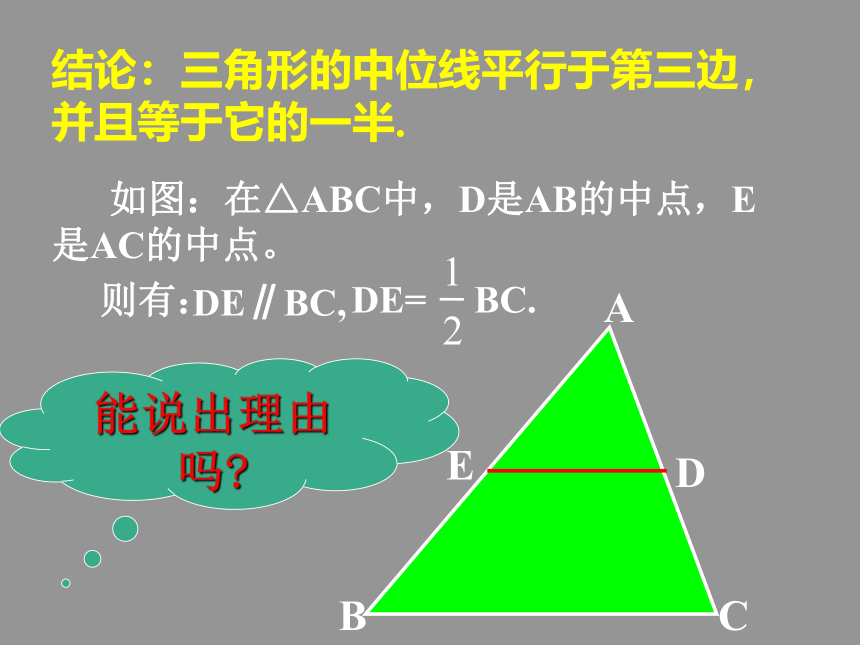
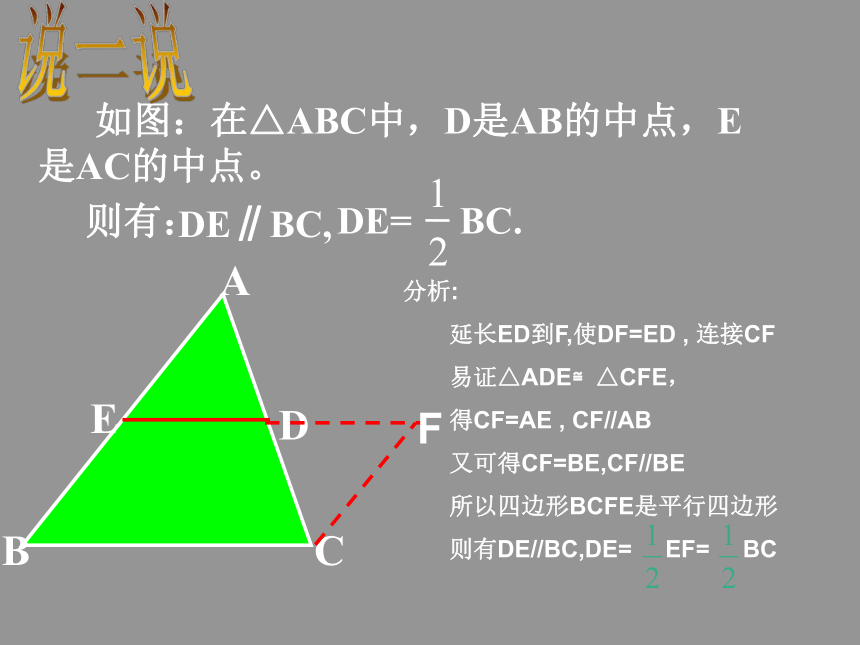
做一做 四边形BCFD是平行四边形吗?说说你的理由!想一想DEDE是三角形ABC的中位线三角形的中位线 连接三角形两边中点的线段叫做三角形的中位线。画出三角形的所有中线并说出中位线和中线的区别.DEF观察猜想 在△ABC中，中位线DE和边BC什么关系?DE和边BC关系数量关系：位置关系：DE= BC.DE结论：三角形的中位线平行于第三边，并且等于它的一半.能说出理由吗?说一说分析:
延长ED到F,使DF=ED , 连接CF
易证△ADE≌△CFE，
得CF=AE , CF//AB
又可得CF=BE,CF//BE
所以四边形BCFE是平行四边形
则有DE//BC,DE= EF= BC
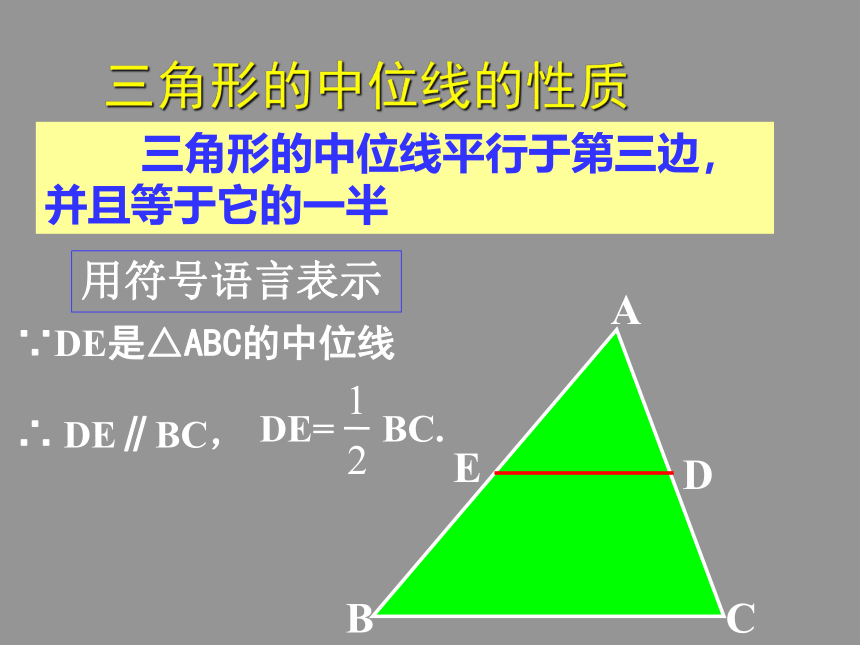
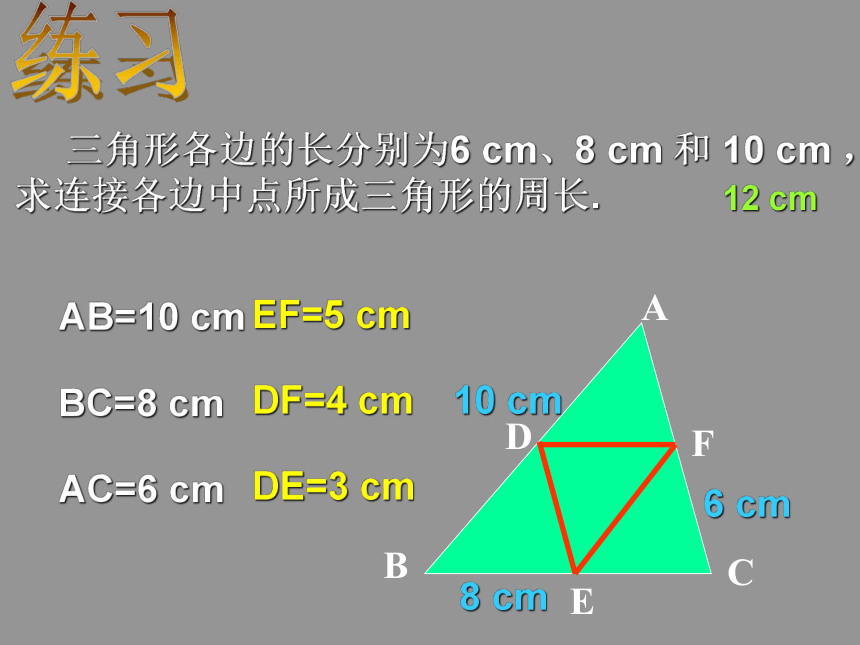
三角形的中位线的性质 三角形的中位线平行于第三边，并且等于它的一半练习 三角形各边的长分别为6 cm、8 cm 和 10 cm ，求连接各边中点所成三角形的周长.AB=10 cmBC=8 cmAC=6 cmEF=5 cmDF=4 cmDE=3 cm12 cmABC测出MN的长，就可知A、B两点的距离
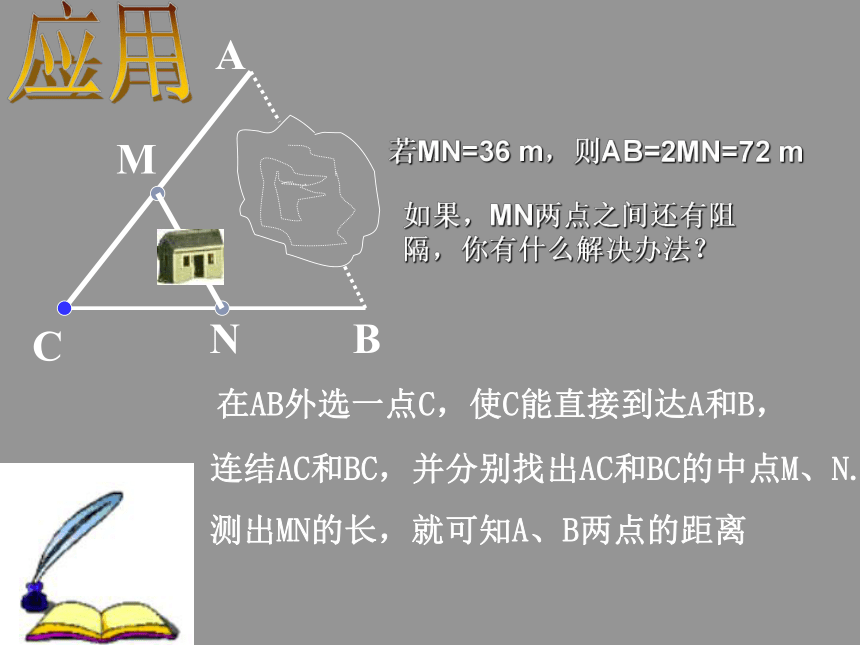
MN应用在AB外选一点C，使C能直接到达A和B，连结AC和BC，并分别找出AC和BC的中点M、N.若MN=36 m，则AB=2MN=72 m如果，MN两点之间还有阻隔，你有什么解决办法？例1、如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是平行四边形吗？为什么？
动动脑从例1中你能得到什么结论？ 顺次连接四边形各边中点的线段组成一个平行四边形 顺次连接矩形各边中点的线段组成一个菱形 （1）?顺次连结平行四边形各边中点所得的四边形是什么？（2）顺次连结菱形各边中点所得的四边形是什么？平行四边形矩形 （3）顺次连结正方形各边中点所得的四边形是什么？ 正方形（4）顺次连结梯形各边中点所得的四边形是什么？（5）顺次连结等腰梯形各边中点所得的四边形是什么？平行四边形菱形 顺次连接四边形各边中点所得到的四边形一定是平行四边形，但它是否是特殊的平行四边形取决于什么呢？议一议拓展 （6）顺次连结对角线相等的四边形各边中点所得的四边形是什么？（8）顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么？ （7）顺次连结对角线垂直的四边形各边中点所得的四边形是什么？菱形矩形正方形结 论互相垂直矩形相等菱形互相垂直且相等正方形既不互相垂直也不相等平行四边形 实际上，顺次连接四边形各边中点所得到的四边形一定是平行四边形，但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等，与是否互相平分无关.游戏（GAME）平行四边形矩 形菱 形正方形1、顺次连接四边形各边中点得到的是平行四边形矩 形菱 形正方形2、顺次连接矩形各边中点得到的是平行四边形矩 形菱 形正方形3、顺次连接菱形各边中点得到的是平行四边形矩 形菱 形正方形4、顺次连接四边形各边中点得到正方形，那么这个四边形是平行四边形矩 形菱 形正方形5、顺次连接四边形各边中点得到菱形，那么这个四边形是平行四边形矩 形菱 形正方形6、顺次连接对角线互相平分的四边形各边中点得到的是
平行四边形矩 形菱 形正方形7、顺次连接对角线互相垂直的四边形各边中点得到的是平行四边形矩 形菱 形正方形8、顺次连接对角线相等的四边形各边中点得到的是小结真聪明！返 回错了！请重新返回思考一下 !返 回你真聪明！返 回请你慎重选择！返回再思考返 回返 回错啦！仔细考虑一下返 回很好！继续保持返 回错了！好好思考返 回真聪明！继续努力返 回答错了！返回吧返 回真聪明！返 回答错了！返 回真聪明！返 回返 回错啦！仔细考虑一下真聪明！返 回返 回错了！好好思考 如图，在矩形ABCD中，E、F、G、H分别是边AB、BC、CD、AD的中点，试说明四边形EFGH是菱形.解：连接AC、BD
根据三角形中位线定理，可得
EF=HG= AC，EH=FG= BD
又在矩形ABCD中，AC=BD
所以，EF=FG=HG=HE
即四边形EFGH是菱形.
小结1.三角形的中位线定义.2.三角形的中位线定理.3.三角形的中位线定理不仅给出了中位线与第三边的关系，而且给出了他们的数量关系，在三角形中给出一边的中点时，要转化为中位线.4.线段的倍分要转化为相等问题来解决.5.三角形的中位线定理的发现过程所用到的数学方法（包括画图、实验、猜想、分析、归纳等.)作业1、随堂练习
2、学习手册