7.4由三角函数求锐角 苏科版初中数学九年级下册同步练习(含解析)
文档属性
| 名称 | 7.4由三角函数求锐角 苏科版初中数学九年级下册同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 590.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
7.4由三角函数求锐角苏科版初中数学九年级下册同步练习
第I卷(选择题)
一、选择题(本大题共7小题,共21分。在每小题列出的选项中,选出符合题目的一项)
1.中,,,,分别是,,的对边,,运用计算器计算,的度数为精确到 ( )
A. B. C. D.
2.锐角满足,利用计算器求时,依次按键则计算器上显示的结果是( )
A. B. C. D.
3.若用我们数学课本上采用的科学计算器计算,按键顺序正确的是( )
A. B.
C. D.
4.若用科学计算器计算,按键顺序正确的是( )
A.
B.
C.
D.
5.若用我们数学课本上采用的科学计算器计算,按键顺序正确的是( )
A.
B.
C.
D.
6.如图是我们数学课本上采用的科学计算器面板,利用该型号计算器计算,按键顺序正确的是( )
A.
B.
C.
D.
7.为了方便行人推车过某天桥,市政府在高的天桥一侧修建了长的斜道如图所示,我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
A. B.
C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
8.如图,将一张矩形纸片沿折叠,点恰好落在边上,设此点为若,则 精确到
9.已知是方程的一个根,是三角形的一个内角,那么的值为__________.
10.在中,,,,则的大小为______精确到.
11.要把长为的梯子上端放在距地面高的阳台边沿上,则梯子摆放时与地面所成的角度约为 精确到
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
12.本小题分
如图,秋千的长为,当秋千摆动到位置时,点相对于最低点升高了求精确到.
13.本小题分
如图,已知内接于,为的直径,,交的延长线于点.
若为的中点,连接,求证:是的切线;
若,求的大小.
14.本小题分
根据下列三角函数值,求锐角精确到:
;.
15.本小题分
在等腰三角形中,,求精确到
16.本小题分
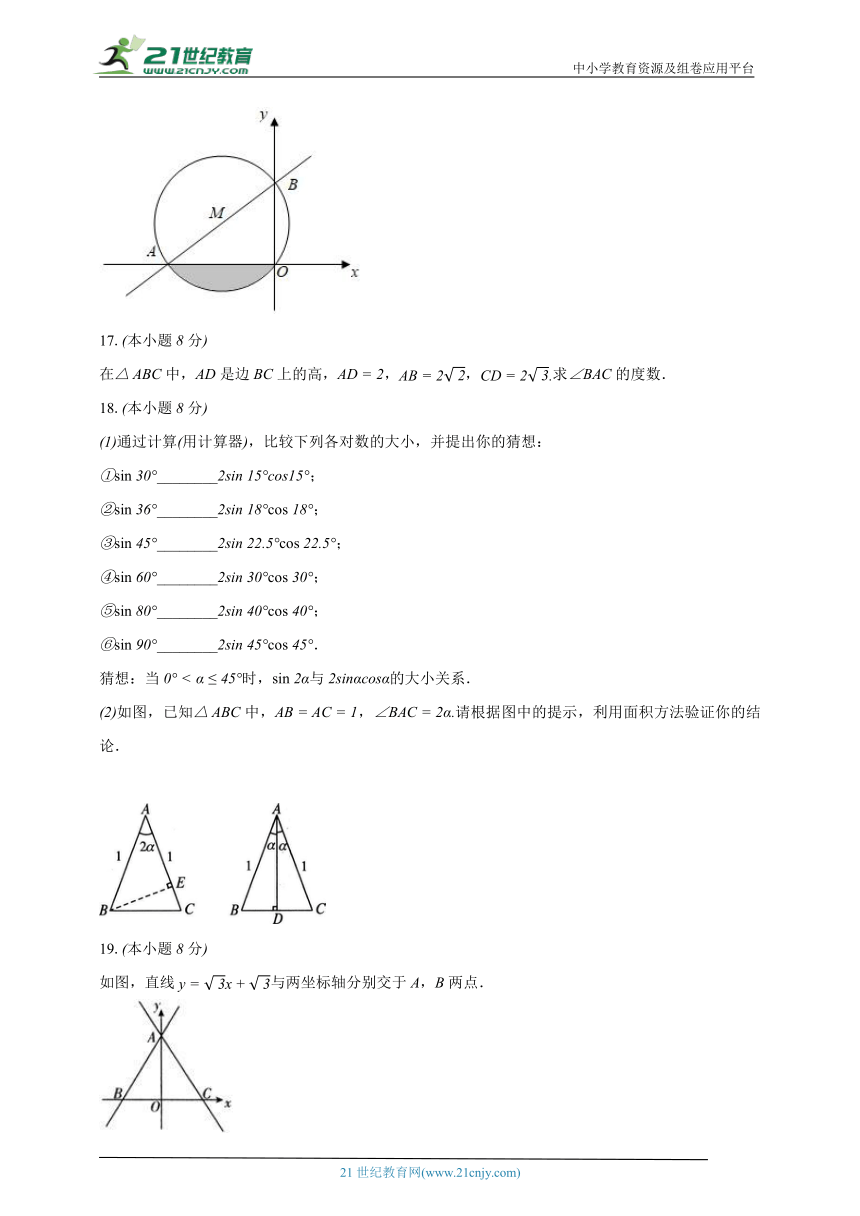
一次函数的图象与轴的负半轴相交于点,与轴的正半轴相交于点,且的外接圆的圆心的横坐标为.
求一次函数的解析式;
求图中阴影部分的面积.
17.本小题分
在中,是边上的高,,,求的度数.
18.本小题分
通过计算用计算器,比较下列各对数的大小,并提出你的猜想:
________;
________;
________;
________;
________;
________.
猜想:当时,与的大小关系.
如图,已知中,,请根据图中的提示,利用面积方法验证你的结论.
19.本小题分
如图,直线与两坐标轴分别交于,两点.
求的度数;
过点的直线交轴正半轴于,,求直线的函数表达式.
20.本小题分
如图,一段公路弯道呈圆弧形,测得弯道两端的距离,的半径为求弯道的长精确到
答案和解析
1.【答案】
【解析】,设,,由勾股定理知,,,运用计算器计算得故选B.
2.【答案】
【解析】,故选C.
3.【答案】
【解析】根据科学计算器的使用方法,可知选D.
4.【答案】
【解析】用科学计算器计算,按键顺序正确的是故选 D.
5.【答案】
【解析】若用我们数学课本上采用的科学计算器计算,按键顺序正确的是故选C.
6.【答案】
【解析】【分析】
本题主要考查了计算器三角函数,要求学生对计算器上的各个功能键熟练掌握,会根据按键顺序列出所要计算的式子.借助计算器这样的工具做题既锻炼了学生动手能力,又提高了学生学习的兴趣.
简单的电子计算器工作顺序是先输入者先算,根据按键顺序写出式子,即可得出答案.
【解答】
解:利用该型号计算器计算,按键顺序正确的是:
故选:.
7.【答案】
【解析】 【分析】
本题考查了计算器的正确使用和三角函数,先利用正弦的定义得到,然后利用计算器求锐角所以用科学计算器求这条斜道倾斜角的度数时,按键顺序为
【解答】
解:,
所以用科学计算器求这条斜道倾斜角的度数时,按键顺序为.
故选A.
8.【答案】
【解析】由折叠可知,.
在矩形中,,,
.
9.【答案】
【解析】【分析】
本题考查的是一元二次方程的根即方程的解的定义及特殊三角函数值有关知识,将代入已知方程,列出关于的值,然后根据特殊角的三角形函数值求得的数值.最后根据锐角来求的值
【解答】
解:是方程的一个根,
满足方程,
,
解得,.
是锐角,
,
故答案是.
10.【答案】
【解析】解:在中,,,,
,
,
故答案为:.
依据,即可得到的大小.
本题主要考查了三角函数,用计算器可以求出任意锐角的三角函数值,也可以根据三角函数值求出锐角的度数.
11.【答案】
【解析】解:如图,由题意得,,,
,,
故答案为:.
12.【答案】解:秋千摆动到位置时,点相对于最低点升高了,
,
,
在中,,
.
【解析】本题考查锐角三角函数的定义,解题的关键是明确题意,找出所求问题需要的条件.
易求的长,在直角三角形中,利用的余弦值即可求出的度数.
13.【答案】证明:连接,,如图,
,
,
,为的中点,
,
,,
,
在与中,
≌,
,
是的切线;
解:为的直径,
,
,
易证∽,
,
,
,
,
,
.
【解析】本题主要考查了切线的判定,相似三角形的判定和性质,全等三角形的判定和性质,直角三角形的性质,平行线的性质,等腰三角形的性质,圆周角定理及其推论,特殊角三角函数值,正确的作出辅助线是解题的关键.
想要证明是的切线,证明即可,连接,,证明≌,得到;
证明∽,得到,即,根据,得到,,即可得到的度数.
14.【答案】解:依次按键,
显示结果为,即;
依次按键,
显示结果为,即.
【解析】见答案
15.【答案】解:如图,过点作,垂足为.
在中,,,
则.
用计算器计算,得.
【解析】见答案
16.【答案】解:作,
由垂径定理得:点为的中点,
,
,
,即,
,,
,
即,
设,将、带入得:,
,,
,则,
,
阴影部分面积为.
【解析】本题为一次函数综合运用题,主要考查了一次函数表达式和图形面积的求法,本题的关键是垂径定理的运用,题目难度不大.
由垂径定理得:点为的中点,,则,即,而,,则,即可求解;
,,,则,则,即,即可求解.
17.【答案】解:如图.
是边上的高,
于.
在直角三角形中,,,,
,
.
在直角三角形中,,,,
,
.
当在内部时,;
当在外部时,.
故的度数为或.
【解析】本题考查了解直角三角形,利用数形结合与分类讨论是解题的关键.
先由是边上的高得出于,再解直角三角形得出,解直角三角形,得出,然后分在内部与在外部两种情况分别求出的度数.
18.【答案】解:都填“”.
,
,
.
【解析】见答案
19.【答案】解:对于直线,
令,则,
令,则,
故点的坐标为,点的坐标为,
则,,
在中,
,
;
在中,
,,
为的中垂线,
即,
则点的坐标为,
设直线的解析式为:为常数,
则
解得:
即直线的函数解析式为:.
【解析】本题考查了待定系数法求一次函数解析式,涉及了的知识点有:待定系数法确定一次函数解析式,一次函数与坐标轴的交点,坐标与图形性质,熟练掌握待定系数法是解答本题的关键.
根据函数解析式求出点、的坐标,然后在中,利用三角函数求出的值,继而可求出的度数;
根据题意可得,,,可得为的中垂线,根据点的坐标,得出点的坐标,然后利用待定系数法求出直线的函数解析式.
20.【答案】解:如图,作,垂足为,则平分.
在中,,,
所以,
由计算器可知,得
所以弯道的长约为米
【解析】见答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.4由三角函数求锐角苏科版初中数学九年级下册同步练习
第I卷(选择题)
一、选择题(本大题共7小题,共21分。在每小题列出的选项中,选出符合题目的一项)
1.中,,,,分别是,,的对边,,运用计算器计算,的度数为精确到 ( )
A. B. C. D.
2.锐角满足,利用计算器求时,依次按键则计算器上显示的结果是( )
A. B. C. D.
3.若用我们数学课本上采用的科学计算器计算,按键顺序正确的是( )
A. B.
C. D.
4.若用科学计算器计算,按键顺序正确的是( )
A.
B.
C.
D.
5.若用我们数学课本上采用的科学计算器计算,按键顺序正确的是( )
A.
B.
C.
D.
6.如图是我们数学课本上采用的科学计算器面板,利用该型号计算器计算,按键顺序正确的是( )
A.
B.
C.
D.
7.为了方便行人推车过某天桥,市政府在高的天桥一侧修建了长的斜道如图所示,我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
A. B.
C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
8.如图,将一张矩形纸片沿折叠,点恰好落在边上,设此点为若,则 精确到
9.已知是方程的一个根,是三角形的一个内角,那么的值为__________.
10.在中,,,,则的大小为______精确到.
11.要把长为的梯子上端放在距地面高的阳台边沿上,则梯子摆放时与地面所成的角度约为 精确到
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
12.本小题分
如图,秋千的长为,当秋千摆动到位置时,点相对于最低点升高了求精确到.
13.本小题分
如图,已知内接于,为的直径,,交的延长线于点.
若为的中点,连接,求证:是的切线;
若,求的大小.
14.本小题分
根据下列三角函数值,求锐角精确到:
;.
15.本小题分
在等腰三角形中,,求精确到
16.本小题分
一次函数的图象与轴的负半轴相交于点,与轴的正半轴相交于点,且的外接圆的圆心的横坐标为.
求一次函数的解析式;
求图中阴影部分的面积.
17.本小题分
在中,是边上的高,,,求的度数.
18.本小题分
通过计算用计算器,比较下列各对数的大小,并提出你的猜想:
________;
________;
________;
________;
________;
________.
猜想:当时,与的大小关系.
如图,已知中,,请根据图中的提示,利用面积方法验证你的结论.
19.本小题分
如图,直线与两坐标轴分别交于,两点.
求的度数;
过点的直线交轴正半轴于,,求直线的函数表达式.
20.本小题分
如图,一段公路弯道呈圆弧形,测得弯道两端的距离,的半径为求弯道的长精确到
答案和解析
1.【答案】
【解析】,设,,由勾股定理知,,,运用计算器计算得故选B.
2.【答案】
【解析】,故选C.
3.【答案】
【解析】根据科学计算器的使用方法,可知选D.
4.【答案】
【解析】用科学计算器计算,按键顺序正确的是故选 D.
5.【答案】
【解析】若用我们数学课本上采用的科学计算器计算,按键顺序正确的是故选C.
6.【答案】
【解析】【分析】
本题主要考查了计算器三角函数,要求学生对计算器上的各个功能键熟练掌握,会根据按键顺序列出所要计算的式子.借助计算器这样的工具做题既锻炼了学生动手能力,又提高了学生学习的兴趣.
简单的电子计算器工作顺序是先输入者先算,根据按键顺序写出式子,即可得出答案.
【解答】
解:利用该型号计算器计算,按键顺序正确的是:
故选:.
7.【答案】
【解析】 【分析】
本题考查了计算器的正确使用和三角函数,先利用正弦的定义得到,然后利用计算器求锐角所以用科学计算器求这条斜道倾斜角的度数时,按键顺序为
【解答】
解:,
所以用科学计算器求这条斜道倾斜角的度数时,按键顺序为.
故选A.
8.【答案】
【解析】由折叠可知,.
在矩形中,,,
.
9.【答案】
【解析】【分析】
本题考查的是一元二次方程的根即方程的解的定义及特殊三角函数值有关知识,将代入已知方程,列出关于的值,然后根据特殊角的三角形函数值求得的数值.最后根据锐角来求的值
【解答】
解:是方程的一个根,
满足方程,
,
解得,.
是锐角,
,
故答案是.
10.【答案】
【解析】解:在中,,,,
,
,
故答案为:.
依据,即可得到的大小.
本题主要考查了三角函数,用计算器可以求出任意锐角的三角函数值,也可以根据三角函数值求出锐角的度数.
11.【答案】
【解析】解:如图,由题意得,,,
,,
故答案为:.
12.【答案】解:秋千摆动到位置时,点相对于最低点升高了,
,
,
在中,,
.
【解析】本题考查锐角三角函数的定义,解题的关键是明确题意,找出所求问题需要的条件.
易求的长,在直角三角形中,利用的余弦值即可求出的度数.
13.【答案】证明:连接,,如图,
,
,
,为的中点,
,
,,
,
在与中,
≌,
,
是的切线;
解:为的直径,
,
,
易证∽,
,
,
,
,
,
.
【解析】本题主要考查了切线的判定,相似三角形的判定和性质,全等三角形的判定和性质,直角三角形的性质,平行线的性质,等腰三角形的性质,圆周角定理及其推论,特殊角三角函数值,正确的作出辅助线是解题的关键.
想要证明是的切线,证明即可,连接,,证明≌,得到;
证明∽,得到,即,根据,得到,,即可得到的度数.
14.【答案】解:依次按键,
显示结果为,即;
依次按键,
显示结果为,即.
【解析】见答案
15.【答案】解:如图,过点作,垂足为.
在中,,,
则.
用计算器计算,得.
【解析】见答案
16.【答案】解:作,
由垂径定理得:点为的中点,
,
,
,即,
,,
,
即,
设,将、带入得:,
,,
,则,
,
阴影部分面积为.
【解析】本题为一次函数综合运用题,主要考查了一次函数表达式和图形面积的求法,本题的关键是垂径定理的运用,题目难度不大.
由垂径定理得:点为的中点,,则,即,而,,则,即可求解;
,,,则,则,即,即可求解.
17.【答案】解:如图.
是边上的高,
于.
在直角三角形中,,,,
,
.
在直角三角形中,,,,
,
.
当在内部时,;
当在外部时,.
故的度数为或.
【解析】本题考查了解直角三角形,利用数形结合与分类讨论是解题的关键.
先由是边上的高得出于,再解直角三角形得出,解直角三角形,得出,然后分在内部与在外部两种情况分别求出的度数.
18.【答案】解:都填“”.
,
,
.
【解析】见答案
19.【答案】解:对于直线,
令,则,
令,则,
故点的坐标为,点的坐标为,
则,,
在中,
,
;
在中,
,,
为的中垂线,
即,
则点的坐标为,
设直线的解析式为:为常数,
则
解得:
即直线的函数解析式为:.
【解析】本题考查了待定系数法求一次函数解析式,涉及了的知识点有:待定系数法确定一次函数解析式,一次函数与坐标轴的交点,坐标与图形性质,熟练掌握待定系数法是解答本题的关键.
根据函数解析式求出点、的坐标,然后在中,利用三角函数求出的值,继而可求出的度数;
根据题意可得,,,可得为的中垂线,根据点的坐标,得出点的坐标,然后利用待定系数法求出直线的函数解析式.
20.【答案】解:如图,作,垂足为,则平分.
在中,,,
所以,
由计算器可知,得
所以弯道的长约为米
【解析】见答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
