7.6用锐角三角函数解决问题 苏科版初中数学九年级下册同步练习(含解析)
文档属性
| 名称 | 7.6用锐角三角函数解决问题 苏科版初中数学九年级下册同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 843.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
7.6用锐角三角函数解决问题苏科版初中数学九年级下册同步练习
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
1.如图,小亮为了测量校园里教学楼的高度,将测角仪竖直放置在与教学楼水平距离为的地面上,若测角仪的高度是测得教学楼的顶部处的仰角为则教学楼的高度是( )
A. B. C. D.
2.如图,小明在处测得处的俯角为,处的俯角为,,,若斜面坡度为:,则斜坡的长是( )
A.
B.
C.
D.
3.马颊大桥是馆聊高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点测得大桥主架与水面的交汇点的俯角为,大桥主架的顶端的仰角为,已知测量点与大桥主架的水平距离,则此时大桥主架顶端离水面的高为
( )
A. B. C. D.
4.如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点,变幅索的底端记为点,垂直地面,垂足为点,,垂足为点设,下列关系式正确的是( )
A. B. C. D.
5.如图,某建筑物的顶部有一块宣传牌,小明在山坡的坡脚处测得宣传牌底部的仰角为,沿山坡向上走到处测得宣传牌顶部的仰角为,已知斜坡的坡角为,米,米,则宣传牌的高度是( )
A.
B.
C.
D.
6.图是第七届国际数学教育大会会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图所示的四边形若,,则的值为.( )
A. B. C. D.
7.某斜坡的坡度:,则该斜坡的坡角为( )
A. B. C. D.
8.如图,一架梯子斜靠在墙上,测得梯子底端到墙角的距离为米,梯子与地面所夹的锐角为,则梯子长( )
A. 米
B. 米
C. 米
D. 米
9.斜坡长为,它的垂直高度为,则坡度等于( )
A. B. C. D.
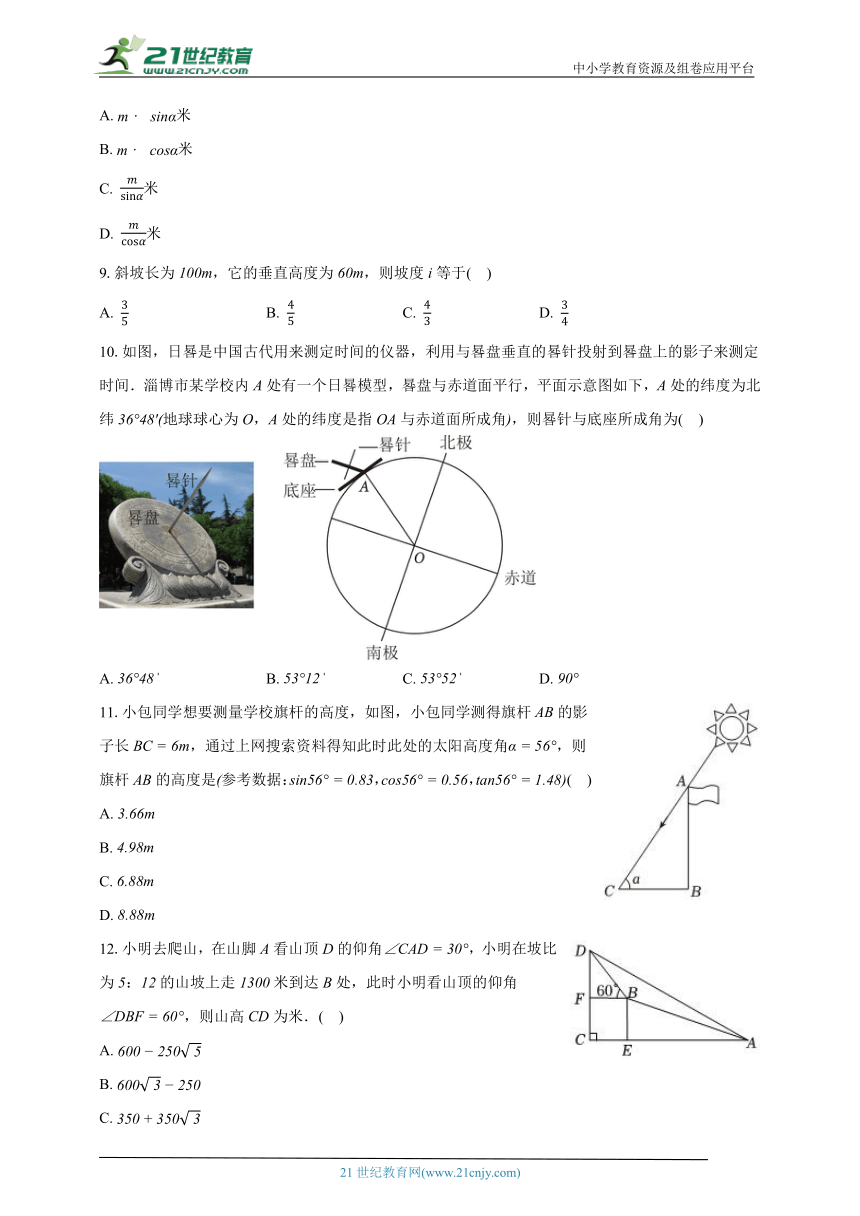
10.如图,日晷是中国古代用来测定时间的仪器,利用与晷盘垂直的晷针投射到晷盘上的影子来测定时间.淄博市某学校内处有一个日晷模型,晷盘与赤道面平行,平面示意图如下,处的纬度为北纬地球球心为,处的纬度是指与赤道面所成角,则晷针与底座所成角为( )
A. B. C. D.
11.小包同学想要测量学校旗杆的高度,如图,小包同学测得旗杆的影子长,通过上网搜索资料得知此时此处的太阳高度角,则旗杆的高度是参考数据:,,( )
A.
B.
C.
D.
12.小明去爬山,在山脚看山顶的仰角,小明在坡比为:的山坡上走米到达处,此时小明看山顶的仰角,则山高为米.( )
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
13.如图,是平面镜,光线从点出发经上点反射后照射到点,若入射角为,反射角为反射角等于入射角,于点,于点,且,,,则的值为______ .
14.如图,准备在宽米的迎宾大道路边安装路灯,设计要求:路灯的灯臂长米,且与灯柱成角,路灯采用圆锥形灯罩,灯罩的轴线与灯臂垂直,灯柱与大道路面垂直,此时恰好为中点.
的度数为______
现在由于道路两边都要装路灯,要求,且灯臂缩短为米,其它的位置关系不变则现在路灯的灯柱高度应该比原设计高度缩短了______ 米
15.数学活动小组欲测量山坡上一棵大树的高度,如图,于点,在处测得大树底端的仰角,沿水平地面前进米到达处,测得大树顶端的仰角,测得山坡坡角图中各点均在同一平面内则这棵大树的高度为______ 结果取整数,参考数据:,,,
16.如图,上午时,一条船从海岛出发,以的速度向正北航行,时到达海岛处,从海岛,处望灯塔,分别测得,,则海岛与灯塔之间的距离是______ .
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
年月日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,是垂直于工作台的移动基座,、为机械臂,,,,机械臂端点到工作台的距离.
求、两点之间的距离;
求长.
结果精确到,参考数据:,,,
18.本小题分
如图,某学习小组在教学楼的顶部观测信号塔底部的俯角为,观测信号塔顶部的仰角为已知教学楼的高度为,求信号塔的高度计算结果保留根号.
19.本小题分
如图,在一笔直的海岸线上有,两个观测站,在的正西方向,,从观测站测得船在北偏东的方向,从观测站测得船在北偏西的方向.求船离观测站的距离.
20.本小题分
宿迁市政府为了方便市民绿色出行,推出了共享单车服务.图是某品牌共享单车放在水平地面上的实物图,图是其示意图,其中、都与地面平行,车轮半径为,,,坐垫与点的距离为.
求坐垫到地面的距离;
根据经验,当坐垫到的距离调整为人体腿长的时,坐骑比较舒适.小明的腿长约为,现将坐垫调整至坐骑舒适高度位置,求的长.
结果精确到,参考数据:,,
21.本小题分
跳台滑雪是冬季奥运会的比赛项目.如图,运动员通过助滑道后在点处腾空,在空中沿抛物线飞行,直至落在着陆坡上的点处.腾空点到地面的距离为,坡高为,着陆坡的坡度即为:以为原点,所在直线为轴,所在直线为轴,建立如图所示的平面直角坐标系.已知这段抛物线经过点,.
求这段抛物线表示的二次函数表达式;
在空中飞行过程中,求运动员到坡面竖直方向上的最大距离;
落点与坡顶之间的距离为______
22.本小题分
如图,公园内有一个垂直于地面的立柱,其旁边有一个坡面,坡角在阳光下,小明观察到在地面上的影长为,在坡面上的影长为同一时刻,小明测得直立于地面长的木杆的影长为其影子完全落在地面上求立柱的高度.
23.本小题分
无人机在实际生活中的应用越来越广泛如图所示,某人利用无人机测量大楼的高度,无人机在空中点处,测得点距地面上点米,点处的俯角为,楼顶点处的俯角为,已知点与大楼的距离为米点,,,在同一平面内,求大楼的高度结果保留根号.
24.本小题分
为测量建筑物的高度,小明从建筑物的处测得处的仰角为,处的俯角为,从处测得处的仰角为已知,,在同一直线上,高为求建筑物的高度.
参考数据:,,
25.本小题分
小淇同学在学习了“平面镜反射原理”后,用一个小平面镜做实验.他先将平面镜放在平面上,如图,用一束与平面成角的光线照射平面镜上的处,使光影正好落在对面墙面上一幅画的底边点.他不改变光线的角度,原地将平面镜转动了角,即,使光影落在点正上方的点,测得求平面镜放置点与墙面的距离参考数据:
答案和解析
1.【答案】
【解析】【分析】
本题考查了解直角三角形,仰角的定义.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键.根据锐角三角函数和直角三角形的性质解答即可.
【解答】
解:过作,则四边形为矩形,
在处测得教学楼顶端的仰角为,
,
,
,
,
故选C.
2.【答案】
【解析】解:斜面坡度为:,
,
,
在处进行观测,测得处的俯角为,处的俯角为,
,,
,
,,
,
,
故选:.
根据三角函数的定义得到,根据已知条件得到,,求得,进一步求得,,即可得到.
此题主要考查了解直角三角形的应用仰角俯角问题,解直角三角形的应用坡度坡角问题,正确得出是解题关键.
3.【答案】
【解析】【分析】
本题考查了解直角三角形仰角俯角问题有关知识,在和中,由三角函数得出,,得出即可.
【解答】
解:在和中,,
,
,
,,
;
故选C.
4.【答案】
【解析】解:在中,,,由锐角三角函数的定义可知,
,
故选:.
根据直角三角形的边角关系进行判断即可.
本题考查解直角三角形的应用,掌握直角三角形的边角关系是正确判断的前提.
5.【答案】
【解析】解:过作,交的延长线于,作于.
在中,,米,
米,米.
米,
在中,,
是等腰直角三角形,
米,
在中,,米,
米,
米,
即宣传牌的高度是米,
故选:.
过作,交的延长线于,作于分别在和中,解直角三角形求出、、的长,可求出即的长;再证,由此可求出的长;然后根据即可求出宣传牌的高度.
本题考查了解直角三角形的应用仰角俯角问题、坡度坡角问题,正确作出辅助线构造直角三角形是解题的关键.
6.【答案】
【解析】解:,
在中,,
,
在中,.
故选:.
在中,,可得的长度,在中,,代入即可得出答案.
本题主要考查了解直角三角形的应用,熟练掌握解直角三角形的方法进行计算是解决本题的关键.
7.【答案】
【解析】解::,
坡角.
故选:.
坡度坡角的正切值,据此直接解答.
此题主要考查学生对坡度及坡角的理解及掌握,关键是坡度坡角的正切值解答.
8.【答案】
【解析】解:,
,
在中,
米,故D正确.
故选:.
根据的余弦值进行求解即可.
本题主要考查了三角函数的应用,解题的关键是熟练掌握余弦的定义.
9.【答案】
【解析】解:由勾股定理得:
坡面的水平宽度为:,
坡度.
故选:.
根据坡度的定义,竖直距离与水平距离的比求解即可.
本题考查了解直角三角形应用坡度问题,掌握坡度是破面的铅直高度和水平宽度的比是解题的关键.
10.【答案】
【解析】【分析】依据晷盘垂直于晷针,底座与垂直,即可得到晷针与底座所成角等于的大小.
【解答】解:如图所示,设晷针与底座交于点,
,
,
又 ,,
,
即,
,
故选:.
【点评】本题主要考查了平行线的性质以及圆的切线的性质,解决问题的关键是掌握切线的性质以及平行线的性质.
11.【答案】
【解析】解:,,,
,故D正确,
故选:.
根据正切函数定义求出的高度即可.
本题主要考查了解直角三角形的应用,解题的关键是熟练掌握三角函数的定义,准确计算.
12.【答案】
【解析】解:::,
,
::::,
米,
米,
米,
设米,
,
米.
又,
.
即:,
解得,
米,
米.
故选:.
构造两个直角三角形与,分别求解可得与的值,再利用图形关系,进而可求出答案.
本题考查俯角、仰角的定义,要求学生能借助坡比、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
13.【答案】
【解析】解:如图,由题意得:,
,
,
,
同理可得:,
,
,
在和中,
,,
∽,
,
,,,,
,
解得,
经检验,是所列分式方程的解,
则,
故答案为:.
如图见解析,先根据平行线的判定与性质可得,,从而可得,再根据相似三角形的判定证出∽,根据相似三角形的性质可得的长,勾股定理求出的长,即可得解.
本题考查相似三角形的判定和性质,解直角三角形.解题的关键是证明三角形相似.
14.【答案】
【解析】解:,,
,
,
,
故答案为:.
如图,延长,交于点,
在中,,
当米时,点为的中点,
米,
,
米,
在中,,米,
米,
当米时,在中,,
米,
米,,
米,
米,
米,
米,
高度应该比原设计高度缩短了:米,
故答案为:.
利用四边形的内角和即可求出;
延长,交于,由直角三角形的性质求出,的长,即可求出的长,即可解答.
本题考查解直角三角形,解题的关键是延长,交于,构造直角三角形.
15.【答案】米
【解析】解:由题意得,米,
是的一个外角,
,
,
,
在中,,米,
米,
米,
在中,,
米,
米,
这棵大树的高度约为米.
故答案为:米.
根据题意可得米,根据三角形的外角性质可求出,从而得出米.在中,利用锐角三角函数的定义求出,的长,然后在中,利用锐角三角函数的定义求出的长,即可解答.
本题考查了解直角三角形的应用中仰角俯角问题,坡度角问题,解题关键是熟练掌握锐角三角函数的定义并正确运用.
16.【答案】
【解析】解:由题意得:海里,
,,
,
,
海里,
从海岛到灯塔的距离为海里.
故答案为:.
根据三角形的外角的性质,得,那么,故AB.
此题考查了方向角和等腰三角形的性质与判定.此题难度不大,注意掌握数形结合思想的应用.
17.【答案】解:如图,过点作,垂足为,
在中,,,
,,
,,
,,
,
在中,由勾股定理.
故A,两点之间距离为.
过点作,垂足为,
,,
,
在中,由勾股定理.
的长为.
【解析】本题考查了解直角三角形的应用、勾股定理等知识;正确作出辅助线构造直角三角形是解题的关键.
过点作,垂足为,在中,由,,可求和,即可得出的长;
过点作,垂足为,在中,由勾股定理可求出,即的长.
18.【答案】解:如图,过点作,垂足为,
由题意得:,
在中,,
,
在中,,
,
,
信号塔的高度为.
【解析】本题考查了解直角三角形的应用仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
过点作,垂足为,根据题意可得,先在中,利用锐角三角函数的定义求出的长,然后在中,利用锐角三角函数的定义求出的长,最后根据即可得解.
19.【答案】解:如图,过点作于点,
则,
,
设,则,
,
由题意知,
在中,
,
,解得.
经检验,是原方程的根.
.
答:船离观测站的距离为.
【解析】本题考查了解直角三角形的应用方向角问题,解决本题的关键是掌握方向角定义.
如图,过点作于点,从而把斜三角形转化为两个直角三角形,然后在两个直角三角形中利用直角三角形的边角关系列出方程求解即可.
20.【答案】解:如图,过点作于点,
由题意知,,
,
则单车坐垫到地面的高度为;
如图所示,过点作于点,
由题意知,
则,
.
【解析】本题考查解直角三角形的应用,解题的关键是明确题意,利用锐角三角函数进行解答.
作于点,由可得答案;
作于点,先根据求得的长度,再根据可得答案
21.【答案】解:为,
,
设二次函数表达式为,
把,,代入得,解得,
所以二次函数的表达式为;
如图,作轴分别交抛物线和于、两点,
坡高为,着陆坡的坡度即为:,
,即,
设线段的关系式为,则,解得:
所以线段的关系式为,
设,则,
则,
,
当时,的最大值为.
运动员到坡面竖直方向上的最大距离是米;
.
【解析】【分析】
本题考查二次函数的实际应用,根据抛物线上的点求出二次函数的关系式是解题关键.
设二次函数表达式为,把代入可得关系式;
作轴分别交抛物线和于、两点,先求出的关系式,再分别表示出、的纵坐标,计算纵坐标的差可得答案;
计算抛物线和线段的交点的坐标,再利用勾股定理可得答案.
【解答】
见答案;
如图,
由题意得,
解得,舍去,即,
米,米,
米,
米,
故答案为:.
22.【答案】解:延长交于点,过点作于点,
在中,,,
则,,
由题意得:,即,解得:,
又,
,
则,
解得:,
答:立柱的高度为.
【解析】本题考查的是解直角三角形的应用坡度坡角问题、平行投影的应用,掌握锐角三角函数的定义是解题的关键.
延长交于点,过点作于点,根据直角三角形的性质求出,根据余弦的定义求出,根据题意求出,再根据题意列出比例式,计算即可.
23.【答案】解:如图所示:
过作于,过作于,而,
则四边形是矩形,
,,
由题意可得:米,,,米,
米,米,
米,
米,
米,
大楼的高度为米
【解析】过作于,过作于,而,则四边形是矩形,先解,求出,,得到的长度,再解,得到的长即可解决问题.
本题考查的是矩形的判定与性质,解直角三角形的实际应用,理解仰角与俯角的含义是解本题的关键.
24.【答案】解:过点作,垂足为,
由题意得:
,,,,
,
在中,,
设,
,
在中,,
,
在中,,
,
,
,
解得:,
,
建筑物的高度约为.
【解析】过点作,垂足为,根据题意可得:,,,,从而可得,然后在中,利用锐角三角函数的定义求出的长,设,则,再在中,利用锐角三角函数的定义求出的长,最后在中,利用锐角三角函数的定义求出的长,从而根据,列出关于的方程,进行计算即可解答.
本题考查了解直角三角形的应用仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
25.【答案】解:由题意得:.
设,则,
在中,,
,
,
,
,
.
因此,平面镜放置点与墙面的距离是.
【解析】本题考查解直角三角形的应用,解题的关键是学会利用参数,构建方程解决问题,属于中考常考题型.
设,则,根据,构建方程求解即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.6用锐角三角函数解决问题苏科版初中数学九年级下册同步练习
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
1.如图,小亮为了测量校园里教学楼的高度,将测角仪竖直放置在与教学楼水平距离为的地面上,若测角仪的高度是测得教学楼的顶部处的仰角为则教学楼的高度是( )
A. B. C. D.
2.如图,小明在处测得处的俯角为,处的俯角为,,,若斜面坡度为:,则斜坡的长是( )
A.
B.
C.
D.
3.马颊大桥是馆聊高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点测得大桥主架与水面的交汇点的俯角为,大桥主架的顶端的仰角为,已知测量点与大桥主架的水平距离,则此时大桥主架顶端离水面的高为
( )
A. B. C. D.
4.如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点,变幅索的底端记为点,垂直地面,垂足为点,,垂足为点设,下列关系式正确的是( )
A. B. C. D.
5.如图,某建筑物的顶部有一块宣传牌,小明在山坡的坡脚处测得宣传牌底部的仰角为,沿山坡向上走到处测得宣传牌顶部的仰角为,已知斜坡的坡角为,米,米,则宣传牌的高度是( )
A.
B.
C.
D.
6.图是第七届国际数学教育大会会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图所示的四边形若,,则的值为.( )
A. B. C. D.
7.某斜坡的坡度:,则该斜坡的坡角为( )
A. B. C. D.
8.如图,一架梯子斜靠在墙上,测得梯子底端到墙角的距离为米,梯子与地面所夹的锐角为,则梯子长( )
A. 米
B. 米
C. 米
D. 米
9.斜坡长为,它的垂直高度为,则坡度等于( )
A. B. C. D.
10.如图,日晷是中国古代用来测定时间的仪器,利用与晷盘垂直的晷针投射到晷盘上的影子来测定时间.淄博市某学校内处有一个日晷模型,晷盘与赤道面平行,平面示意图如下,处的纬度为北纬地球球心为,处的纬度是指与赤道面所成角,则晷针与底座所成角为( )
A. B. C. D.
11.小包同学想要测量学校旗杆的高度,如图,小包同学测得旗杆的影子长,通过上网搜索资料得知此时此处的太阳高度角,则旗杆的高度是参考数据:,,( )
A.
B.
C.
D.
12.小明去爬山,在山脚看山顶的仰角,小明在坡比为:的山坡上走米到达处,此时小明看山顶的仰角,则山高为米.( )
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
13.如图,是平面镜,光线从点出发经上点反射后照射到点,若入射角为,反射角为反射角等于入射角,于点,于点,且,,,则的值为______ .
14.如图,准备在宽米的迎宾大道路边安装路灯,设计要求:路灯的灯臂长米,且与灯柱成角,路灯采用圆锥形灯罩,灯罩的轴线与灯臂垂直,灯柱与大道路面垂直,此时恰好为中点.
的度数为______
现在由于道路两边都要装路灯,要求,且灯臂缩短为米,其它的位置关系不变则现在路灯的灯柱高度应该比原设计高度缩短了______ 米
15.数学活动小组欲测量山坡上一棵大树的高度,如图,于点,在处测得大树底端的仰角,沿水平地面前进米到达处,测得大树顶端的仰角,测得山坡坡角图中各点均在同一平面内则这棵大树的高度为______ 结果取整数,参考数据:,,,
16.如图,上午时,一条船从海岛出发,以的速度向正北航行,时到达海岛处,从海岛,处望灯塔,分别测得,,则海岛与灯塔之间的距离是______ .
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
年月日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,是垂直于工作台的移动基座,、为机械臂,,,,机械臂端点到工作台的距离.
求、两点之间的距离;
求长.
结果精确到,参考数据:,,,
18.本小题分
如图,某学习小组在教学楼的顶部观测信号塔底部的俯角为,观测信号塔顶部的仰角为已知教学楼的高度为,求信号塔的高度计算结果保留根号.
19.本小题分
如图,在一笔直的海岸线上有,两个观测站,在的正西方向,,从观测站测得船在北偏东的方向,从观测站测得船在北偏西的方向.求船离观测站的距离.
20.本小题分
宿迁市政府为了方便市民绿色出行,推出了共享单车服务.图是某品牌共享单车放在水平地面上的实物图,图是其示意图,其中、都与地面平行,车轮半径为,,,坐垫与点的距离为.
求坐垫到地面的距离;
根据经验,当坐垫到的距离调整为人体腿长的时,坐骑比较舒适.小明的腿长约为,现将坐垫调整至坐骑舒适高度位置,求的长.
结果精确到,参考数据:,,
21.本小题分
跳台滑雪是冬季奥运会的比赛项目.如图,运动员通过助滑道后在点处腾空,在空中沿抛物线飞行,直至落在着陆坡上的点处.腾空点到地面的距离为,坡高为,着陆坡的坡度即为:以为原点,所在直线为轴,所在直线为轴,建立如图所示的平面直角坐标系.已知这段抛物线经过点,.
求这段抛物线表示的二次函数表达式;
在空中飞行过程中,求运动员到坡面竖直方向上的最大距离;
落点与坡顶之间的距离为______
22.本小题分
如图,公园内有一个垂直于地面的立柱,其旁边有一个坡面,坡角在阳光下,小明观察到在地面上的影长为,在坡面上的影长为同一时刻,小明测得直立于地面长的木杆的影长为其影子完全落在地面上求立柱的高度.
23.本小题分
无人机在实际生活中的应用越来越广泛如图所示,某人利用无人机测量大楼的高度,无人机在空中点处,测得点距地面上点米,点处的俯角为,楼顶点处的俯角为,已知点与大楼的距离为米点,,,在同一平面内,求大楼的高度结果保留根号.
24.本小题分
为测量建筑物的高度,小明从建筑物的处测得处的仰角为,处的俯角为,从处测得处的仰角为已知,,在同一直线上,高为求建筑物的高度.
参考数据:,,
25.本小题分
小淇同学在学习了“平面镜反射原理”后,用一个小平面镜做实验.他先将平面镜放在平面上,如图,用一束与平面成角的光线照射平面镜上的处,使光影正好落在对面墙面上一幅画的底边点.他不改变光线的角度,原地将平面镜转动了角,即,使光影落在点正上方的点,测得求平面镜放置点与墙面的距离参考数据:
答案和解析
1.【答案】
【解析】【分析】
本题考查了解直角三角形,仰角的定义.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键.根据锐角三角函数和直角三角形的性质解答即可.
【解答】
解:过作,则四边形为矩形,
在处测得教学楼顶端的仰角为,
,
,
,
,
故选C.
2.【答案】
【解析】解:斜面坡度为:,
,
,
在处进行观测,测得处的俯角为,处的俯角为,
,,
,
,,
,
,
故选:.
根据三角函数的定义得到,根据已知条件得到,,求得,进一步求得,,即可得到.
此题主要考查了解直角三角形的应用仰角俯角问题,解直角三角形的应用坡度坡角问题,正确得出是解题关键.
3.【答案】
【解析】【分析】
本题考查了解直角三角形仰角俯角问题有关知识,在和中,由三角函数得出,,得出即可.
【解答】
解:在和中,,
,
,
,,
;
故选C.
4.【答案】
【解析】解:在中,,,由锐角三角函数的定义可知,
,
故选:.
根据直角三角形的边角关系进行判断即可.
本题考查解直角三角形的应用,掌握直角三角形的边角关系是正确判断的前提.
5.【答案】
【解析】解:过作,交的延长线于,作于.
在中,,米,
米,米.
米,
在中,,
是等腰直角三角形,
米,
在中,,米,
米,
米,
即宣传牌的高度是米,
故选:.
过作,交的延长线于,作于分别在和中,解直角三角形求出、、的长,可求出即的长;再证,由此可求出的长;然后根据即可求出宣传牌的高度.
本题考查了解直角三角形的应用仰角俯角问题、坡度坡角问题,正确作出辅助线构造直角三角形是解题的关键.
6.【答案】
【解析】解:,
在中,,
,
在中,.
故选:.
在中,,可得的长度,在中,,代入即可得出答案.
本题主要考查了解直角三角形的应用,熟练掌握解直角三角形的方法进行计算是解决本题的关键.
7.【答案】
【解析】解::,
坡角.
故选:.
坡度坡角的正切值,据此直接解答.
此题主要考查学生对坡度及坡角的理解及掌握,关键是坡度坡角的正切值解答.
8.【答案】
【解析】解:,
,
在中,
米,故D正确.
故选:.
根据的余弦值进行求解即可.
本题主要考查了三角函数的应用,解题的关键是熟练掌握余弦的定义.
9.【答案】
【解析】解:由勾股定理得:
坡面的水平宽度为:,
坡度.
故选:.
根据坡度的定义,竖直距离与水平距离的比求解即可.
本题考查了解直角三角形应用坡度问题,掌握坡度是破面的铅直高度和水平宽度的比是解题的关键.
10.【答案】
【解析】【分析】依据晷盘垂直于晷针,底座与垂直,即可得到晷针与底座所成角等于的大小.
【解答】解:如图所示,设晷针与底座交于点,
,
,
又 ,,
,
即,
,
故选:.
【点评】本题主要考查了平行线的性质以及圆的切线的性质,解决问题的关键是掌握切线的性质以及平行线的性质.
11.【答案】
【解析】解:,,,
,故D正确,
故选:.
根据正切函数定义求出的高度即可.
本题主要考查了解直角三角形的应用,解题的关键是熟练掌握三角函数的定义,准确计算.
12.【答案】
【解析】解:::,
,
::::,
米,
米,
米,
设米,
,
米.
又,
.
即:,
解得,
米,
米.
故选:.
构造两个直角三角形与,分别求解可得与的值,再利用图形关系,进而可求出答案.
本题考查俯角、仰角的定义,要求学生能借助坡比、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
13.【答案】
【解析】解:如图,由题意得:,
,
,
,
同理可得:,
,
,
在和中,
,,
∽,
,
,,,,
,
解得,
经检验,是所列分式方程的解,
则,
故答案为:.
如图见解析,先根据平行线的判定与性质可得,,从而可得,再根据相似三角形的判定证出∽,根据相似三角形的性质可得的长,勾股定理求出的长,即可得解.
本题考查相似三角形的判定和性质,解直角三角形.解题的关键是证明三角形相似.
14.【答案】
【解析】解:,,
,
,
,
故答案为:.
如图,延长,交于点,
在中,,
当米时,点为的中点,
米,
,
米,
在中,,米,
米,
当米时,在中,,
米,
米,,
米,
米,
米,
米,
高度应该比原设计高度缩短了:米,
故答案为:.
利用四边形的内角和即可求出;
延长,交于,由直角三角形的性质求出,的长,即可求出的长,即可解答.
本题考查解直角三角形,解题的关键是延长,交于,构造直角三角形.
15.【答案】米
【解析】解:由题意得,米,
是的一个外角,
,
,
,
在中,,米,
米,
米,
在中,,
米,
米,
这棵大树的高度约为米.
故答案为:米.
根据题意可得米,根据三角形的外角性质可求出,从而得出米.在中,利用锐角三角函数的定义求出,的长,然后在中,利用锐角三角函数的定义求出的长,即可解答.
本题考查了解直角三角形的应用中仰角俯角问题,坡度角问题,解题关键是熟练掌握锐角三角函数的定义并正确运用.
16.【答案】
【解析】解:由题意得:海里,
,,
,
,
海里,
从海岛到灯塔的距离为海里.
故答案为:.
根据三角形的外角的性质,得,那么,故AB.
此题考查了方向角和等腰三角形的性质与判定.此题难度不大,注意掌握数形结合思想的应用.
17.【答案】解:如图,过点作,垂足为,
在中,,,
,,
,,
,,
,
在中,由勾股定理.
故A,两点之间距离为.
过点作,垂足为,
,,
,
在中,由勾股定理.
的长为.
【解析】本题考查了解直角三角形的应用、勾股定理等知识;正确作出辅助线构造直角三角形是解题的关键.
过点作,垂足为,在中,由,,可求和,即可得出的长;
过点作,垂足为,在中,由勾股定理可求出,即的长.
18.【答案】解:如图,过点作,垂足为,
由题意得:,
在中,,
,
在中,,
,
,
信号塔的高度为.
【解析】本题考查了解直角三角形的应用仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
过点作,垂足为,根据题意可得,先在中,利用锐角三角函数的定义求出的长,然后在中,利用锐角三角函数的定义求出的长,最后根据即可得解.
19.【答案】解:如图,过点作于点,
则,
,
设,则,
,
由题意知,
在中,
,
,解得.
经检验,是原方程的根.
.
答:船离观测站的距离为.
【解析】本题考查了解直角三角形的应用方向角问题,解决本题的关键是掌握方向角定义.
如图,过点作于点,从而把斜三角形转化为两个直角三角形,然后在两个直角三角形中利用直角三角形的边角关系列出方程求解即可.
20.【答案】解:如图,过点作于点,
由题意知,,
,
则单车坐垫到地面的高度为;
如图所示,过点作于点,
由题意知,
则,
.
【解析】本题考查解直角三角形的应用,解题的关键是明确题意,利用锐角三角函数进行解答.
作于点,由可得答案;
作于点,先根据求得的长度,再根据可得答案
21.【答案】解:为,
,
设二次函数表达式为,
把,,代入得,解得,
所以二次函数的表达式为;
如图,作轴分别交抛物线和于、两点,
坡高为,着陆坡的坡度即为:,
,即,
设线段的关系式为,则,解得:
所以线段的关系式为,
设,则,
则,
,
当时,的最大值为.
运动员到坡面竖直方向上的最大距离是米;
.
【解析】【分析】
本题考查二次函数的实际应用,根据抛物线上的点求出二次函数的关系式是解题关键.
设二次函数表达式为,把代入可得关系式;
作轴分别交抛物线和于、两点,先求出的关系式,再分别表示出、的纵坐标,计算纵坐标的差可得答案;
计算抛物线和线段的交点的坐标,再利用勾股定理可得答案.
【解答】
见答案;
如图,
由题意得,
解得,舍去,即,
米,米,
米,
米,
故答案为:.
22.【答案】解:延长交于点,过点作于点,
在中,,,
则,,
由题意得:,即,解得:,
又,
,
则,
解得:,
答:立柱的高度为.
【解析】本题考查的是解直角三角形的应用坡度坡角问题、平行投影的应用,掌握锐角三角函数的定义是解题的关键.
延长交于点,过点作于点,根据直角三角形的性质求出,根据余弦的定义求出,根据题意求出,再根据题意列出比例式,计算即可.
23.【答案】解:如图所示:
过作于,过作于,而,
则四边形是矩形,
,,
由题意可得:米,,,米,
米,米,
米,
米,
米,
大楼的高度为米
【解析】过作于,过作于,而,则四边形是矩形,先解,求出,,得到的长度,再解,得到的长即可解决问题.
本题考查的是矩形的判定与性质,解直角三角形的实际应用,理解仰角与俯角的含义是解本题的关键.
24.【答案】解:过点作,垂足为,
由题意得:
,,,,
,
在中,,
设,
,
在中,,
,
在中,,
,
,
,
解得:,
,
建筑物的高度约为.
【解析】过点作,垂足为,根据题意可得:,,,,从而可得,然后在中,利用锐角三角函数的定义求出的长,设,则,再在中,利用锐角三角函数的定义求出的长,最后在中,利用锐角三角函数的定义求出的长,从而根据,列出关于的方程,进行计算即可解答.
本题考查了解直角三角形的应用仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
25.【答案】解:由题意得:.
设,则,
在中,,
,
,
,
,
.
因此,平面镜放置点与墙面的距离是.
【解析】本题考查解直角三角形的应用,解题的关键是学会利用参数,构建方程解决问题,属于中考常考题型.
设,则,根据,构建方程求解即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
