5.5用二次函数解决问题 苏科版初中数学九年级下册同步练习(含解析)
文档属性
| 名称 | 5.5用二次函数解决问题 苏科版初中数学九年级下册同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 510.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 13:32:20 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
5.5用二次函数解决问题苏科版初中数学九年级下册同步练习
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
1.如图,正方形的边长为,点和点分别从点和点出发,沿射线向右运动,且速度相同,过点作,垂足为,连接,设点运动的距离为,的面积为,则能反映与之间的函数关系的图象大致为
( )
A. B.
C. D.
2.如图,正方形的边长为,点和点分别从点和点出发,沿射线向右运动,且速度相同,过点作,垂足为,连接,设点运动的距离为,的面积为,则能反映与之间的函数关系的图象大致为
A. B.
C. D.
3.服装店将进价为每件元的服装按每件元出售,每天可销售件,若想获得最大利润,则应定为( )
A. 元 B. 元 C. 元 D. 元
4.某商场销售的某种商品每件的标价是元,若按标价的八折销售,仍可盈利元,市场调查发现:在以标价打八折为销售价的基础上,该种商品每星期可卖出件,该种向品每降价元,每星期可多卖件设每件商品降价元为整数,每星期的利润为元以下说法错误的是( )
A. 每件商品进价为元
B. 降价后每件商品售价为元
C. 降价后每周可卖件
D. 每星期的利润为
5.心理学家发现:课堂上,学生对概念的接受能力与提出概念的时间单位:之间近似满足函数关系,值越大,表示接受能力越强.如图记录了学生学习某概念时与的三组数据,根据上述函数模型和数据,可推断出当学生接受能力最强时,提出概念的时间为
( )
A. B. C. D.
6.一个弹性球从地面竖直向上弹起时的速度为米秒,经过秒时,球距离地面的高度米满足公式,那么球弹起后又回到地面所花的时间是( )
A. B. C. D.
7.某水利工程公司开挖的沟渠,蓄水之后截面呈抛物线形,在图中建立平面直角坐标系,并标出相关数据单位:某学习小组探究之后得出如下结论,其中正确的为( )
A.
B. 池底所在抛物线的解析式为
C. 池塘最深处到水面的距离为
D. 若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的
8.如图,从地面竖直向上抛出一个小球,小球的高度与小球运动时间之间的表达式为,那么小球从抛出至落回到地面所需要的时间是( )
A. B. C. D.
9.在某市治理违建的过程中,某小区拆除了自建房,改建绿地如图,自建房占地是边长为的正方形,改建的绿地的是矩形,其中点在上,点在的延长线上,且那么当为多少时,绿地的面积最大?( )
A.
B.
C.
D.
10.如图,一座拱桥的轮廓是抛物线型,拱高,跨度,相邻两支柱间的距离均为,请根据所给的数据,则支柱的长度为( )
A. B. C. D.
11.如图,以的速度将小球沿与地面成角的方向击出时,小球的飞行路线将是一条抛物线如果不考虑空气阻力,小球的飞行高度单位:与飞行时间单位:之间具有函数关系下列叙述正确的是( )
A. 小球的飞行高度只有在时达到 B. 小球的飞行高度可以达到
C. 小球从飞出到落地要用时 D. 小球飞出时的飞行高度为
12.一个直角三角形的两条直角边长的和为,其中一条直角边长为,三角形的面积为,则与之间的函数解析式为
.( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
13.如图,一位篮球运动员投篮,球沿抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为,则他距篮筐中心的水平距离是
14.如图,某中学综合与实践小组要围成一个矩形菜园,其中一边靠墙,其余的三边,,用总长为米的栅栏围成.设矩形的边米,面积为平方米.
活动区面积与之间的关系式为 ;
菜园最大面积是 平方米.
15.飞机着陆后滑行的距离单位:关于滑行时间单位:的函数解析式是在飞机着陆滑行中,最后滑行的距离是____.
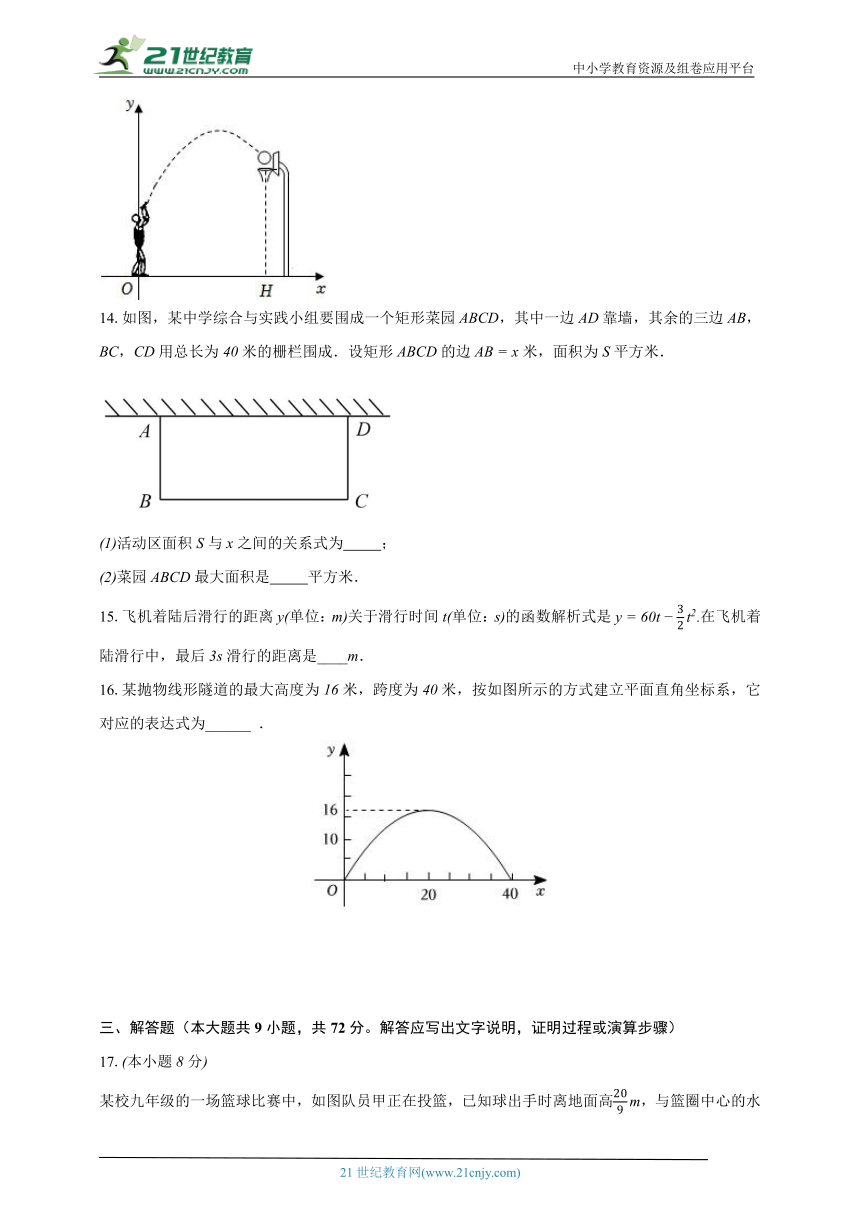
16.某抛物线形隧道的最大高度为米,跨度为米,按如图所示的方式建立平面直角坐标系,它对应的表达式为______ .
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高,与篮圈中心的水平距离为,当球出手后水平距离为时到达最大高度,设篮球运动的轨迹为抛物线,篮圈距地面建立如图所示的平面坐标系,求抛物线的解析式并判断此球能否准确投中?
18.本小题分
如图,用一段长为的篱笆围成一个一边靠墙的矩形花圃,墙长设长为,矩形的面积为问:当长为多少米时,所围成的花圃面积最大?最大面积是多少?
19.本小题分
商场销售某品牌牛奶,已知进价为每箱元经市场调研,售价为元时,可销售箱;售价每提高元,销售量将减少箱当每箱售价为多少元时,才能使利润最大?最大利润是多少元?
20.本小题分
超市销售某种儿童玩具,如果每件利润为元市场管理部门规定,该种玩具每件利润不能超过元,每天可售出件.根据市场调查发现,销售单价每增加元,每天销售量会减少件.设销售单价增加元,每天售出件.
请写出与之间的函数表达式;
当为多少时,超市每天销售这种玩具可获利润元?
设超市每天销售这种玩具可获利元,当为多少时,最大,最大值是多少?
21.本小题分
某超市经销一种商品,每千克成本为元,经试销发现,该种商品的每天销售量千克与销售单价元千克满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
销售单价元千克
销售量千克
求千克与元千克之间的函数表达式;
为保证某天获得元的销售利润,则该天的销售单价应定为多少?
当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?
22.本小题分
如图,一名男生推铅球,铅球行进高度单位:与水平距离单位:之间的关系是.
求:
铅球在行进中的最大高度;
该男生将铅球推出的距离是多少?
23.本小题分
我市某化工材料经销商购进一种化工材料若干千克,成本为每千克元,物价部门规定其销售单价不低于成本价且不高于成本价的倍,经试销发现,日销售量千克与销售单价元符合一次函数关系,如图所示.
求与之间的函数关系式,并写出自变量的取值范围;
若在销售过程中每天还要支付其他费用元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?
24.本小题分
小明进行铅球训练,他尝试利用数学模型来研究铅球的运动情况.他以水平方向为轴方向,为单位长度,建立了如图所示的平面直角坐标系,铅球从轴上的点出手,运动路径可看作抛物线,在点处达到最高位置,落在轴上的点处.小明某次试投时的数据如图所示.
在图中画出铅球运动路径的示意图;
根据图中信息,求出铅球路径所在抛物线的表达式;
若铅球投掷距离铅球落地点与出手点的水平距离的长度不小于,成绩为优秀.请通过计算,判断小明此次试投的成绩是否能达到优秀.
25.本小题分
蚌埠,古乃采珠之地,素有“珍珠城”之美誉,已知一批珍珠每颗的进价为元,售价定为元颗时,每天可销售颗,为扩大市场占有率,商家决定采取适当的降价措施,经调查发现,售价每降低元,每天销量可增加颗销售单价不低于进价.
写出商家每天的利润元与降价元之间的函数关系
当降价多少元时,商家每天的利润最大,最大利润是多少
若商家每天的利润至少要达到元,则定价应在什么范围内
答案和解析
1.【答案】
【解析】解:过点作,垂足为.
是正方形的对角线
是等腰直角三角形
的面积
与之间的函数关系是二次函数,且二次函数图象开口方向向上;
因此,选项中只有选项符合条件.
故选:.
根据正方形的性质得到,由题意得出是等腰直角三角形;过点作的高,同时也是的高;再根据等腰直角三角形的性质求出,也就能求出的面积了.
此题综合性较强,涉及二次函数、等腰三角形等知识,是近年来较为流行的试题,解题的关键在于结合题目的要求动中取静,相信解决这种问题不会非常难.
2.【答案】
【解析】解:过点作,垂足为.
是正方形的对角线
是等腰直角三角形
的面积
与之间的函数关系是二次函数,且二次函数图象开口方向向上;
因此,选项中只有选项符合条件.
故选:.
根据正方形的性质得到,由题意得出是等腰直角三角形;过点作的高,同时也是的高;再根据等腰直角三角形的性质求出,也就能求出的面积了.
此题综合性较强,涉及二次函数、等腰三角形等知识,是近年来较为流行的试题,解题的关键在于结合题目的要求动中取静,相信解决这种问题不会非常难.
3.【答案】
【解析】【分析】
本题考查了二次函数在实际问题中的应用,正确地写出函数关系式,并明确二次函数的性质,是解题的关键.设获得的利润为元,由题意得关于的二次函数,配方,写成顶点式,利用二次函数的性质可得答案.
【解答】
解:设获得的利润为元,由题意得:
,,
当时,取得最大值元.
故选A.
4.【答案】
【解析】解:由题意,设每件商品进价为元,
.
,即可判断A正确,不符合题意.
此时降价后每件商品售价为:,即可判断B正确,不符合题意.
降价后每周可卖件,可以判断C正确,不符合题意.
由上,每星期的利润为,即可判断D错误,符合题意.
故选:.
依据题意,设每件商品进价为元,由,即可判断;降价后每件商品售价为:,即可判断;降价后每周可卖件,可以判断;由上,每星期的利润为,即可判断.
本题主要考查二次函数的应用,解题的关键是理解题意找到其蕴含的相等关系,并据此列出函数解析式,也要求熟练掌握二次函数的性质.
5.【答案】
【解析】【分析】
本题考查了二次函数的性质在实际生活中的应用,首先要吃透题意,确定已知点坐标,求出函数表达式,通常自变量在对称轴时,函数取得最值.
把点坐标:、、,代入函数,求出函数表达式,由,故函数有最大值,即:当时,有最大值.
【解答】
解:由题意得:函数过点、、,
把以上三点坐标代入得:
,解得:,
则函数的表达式为:,
,则函数有最大值,
当时,有最大值,即学生接受能力最强,
故选:.
6.【答案】
【解析】解:令,得:,
解得:或,
那么球弹起后又回到地面所花的时间是秒;
故选:.
根据二次函数的性质即可得到结论.
本题主要考查二次函数的应用,熟练掌握二次函数的图象和性质是解题的关键.
7.【答案】
【解析】解:设池底所在抛物线的解析式为,
把抛物线上点,,,代入抛物线解析式中得:
,
解得:,
解析式为.
选项A中,,故选项A错误,该选项不符合题意;
选项B中,池底所在抛物线的解析式为,故选项B错误,该选项不符合题意;
选项C中,池塘水深最深处为点,水面为,,
,
所以水深最深处为点到水面的距离为,故选项C正确,该选项符合题意;
选项D中,若池塘中水面的宽度由原来的减少到原来的一半为,
由抛物线关于轴对称可知,抛物线上点横坐标,代入解析式算得,
即最深处到水面的距离为米,
而原来最深处到水面的距离为米,减少为原来的故选项D错误,该选项不符合题意.
故选:.
利用建立的坐标系得到抛物线上点的坐标,然后通过待定系数法求出抛物线解析式,根据二次函数的性质对照选项逐一判定即可.
本题考查二次函数的实际应用问题,计算较为复杂,在计算时需要理清楚实际数据在坐标系中对应的位置.能够正确计算和分析实际情况是解题的关键.
8.【答案】
【解析】解:由小球高度与运动时间的关系式.
令,
解得:不合题意,舍去,
,小球从抛出至回落到地面所需要的时间是秒.
故选:.
由小球高度与运动时间的关系式,令,解得的两值之差便是所要求得的结果.
本题考查了运动函数方程,是二次函数的实际应用.
9.【答案】
【解析】解:设,则,绿地的面积为,根据题意得:
.
二次项系数为,
当时,有最大值.
即当时,绿地面积最大.
故选:.
依据题意,设,则,绿地的面积为,根据题意得关于的二次函数,然后写成顶点式,利用二次函数的性质可得答案.
本题考查了二次函数在几何图形问题中的应用,根据题意正确得出所求的面积关于的函数关系式、明确二次函数的相关性质是解题的关键.
10.【答案】
【解析】解:如图所示,建立平面直角坐标系,
由题意得点坐标,点坐标为,点坐标为,点横坐标为,
设抛物线解析式为,
,
,
抛物线解析式为,
当时,,
支柱的高度,
故选:.
如图所示,建立坐标系,然后求出抛物线解析式,然后求出点纵坐标,即可求解.
本题主要考查了二次函数的应用,解题的关键在于能够根据题意正确建立坐标系求解.
11.【答案】
【解析】解:、当时,,
解得:,,
故当或小球的飞行高度能达到,故此选项错误,不符合题意;
B、,
故时,小球的飞行高度最大为:,故此选项错误,不符合题意;
C、时,,
解得:,,
小球从飞出到落地要用时,故此选项错误,不符合题意;
D、由题意,当时,,
故小球飞出时的飞行高度为,故此选项正确,符合题意;
故选:.
依据题意,根据二次函数的性质逐项进行判断即可得解.
本题主要考查了二次函数的应用,正确解方程是解题关键.
12.【答案】
【解析】解:直角三角形的两条直角边的和等于,且它的一条直角边为,
另一条直角边为,
直角三角形的面积,
与之间的函数关系式.
本题考查了二次函数的应用,根据各数量之间的关系,找出与之间的函数关系式是解题的关键.
13.【答案】
【解析】【分析】
此题考查二次函数的运用,根据所建坐标系确定水平距离的求法是此题关键.根据所建坐标系,水平距离就是时离他最远的距离.
【解答】
解:当时,,
,
,
解得:,,
故他距篮筐中心的水平距离是.
故答案为.
14.【答案】
【解析】【分析】本题考查二次函数的应用,
表示出 ,由矩形面积公式可得函数关系式;
把面积配成顶点式,由二次函数性质可得答案.
【详解】解:由题意得: ,
,
,解得 ,
活动区面积与 之间的关系式为 ;
解:由得:活动区面积与 之间的关系式为 ,
,
当 时,取最大值,
菜园 最大面积是平方米;
15.【答案】
【解析】解:当取得最大值时,飞机停下来,
,
即当时,飞机滑行才停下来,
当时,,
,
故答案为.
当取得最大值时,飞机停下来,,即当时,飞机滑行才停下来,当时,,即可求解.
本题考查了二次函数的性质在实际生活中的应用,本题要首先确定飞机最大滑行时间,然后确定最后秒滑行的距离.
16.【答案】
【解析】解:由题意知,抛物线的顶点坐标为,过,
设抛物线对应的表达式为,
将代入得,,
解得,,
,
故答案为:.
由题意知,抛物线的顶点坐标为,过,设抛物线对应的表达式为,将代入得,,解得,,进而可得结果.
本题考查二次函数的应用,解题的关键是灵活应用抛物线的顶点式解决问题,属于中考常考题型.
17.【答案】解:由题意得,抛物线的顶点坐标为,球出手时的坐标为,
设抛物线解析式为:,
将点代入可得:,
解得:,
则抛物线的解析式为:
令,则,
,
此球能准确投中.
【解析】根据抛物线的顶点坐标及球出手时的坐标,可确定抛物线的解析式,令,求出的值,与比较即可作出判断.
本题考查了二次函数的应用,解答本题的关键是利用待定系数法求出抛物线解析式,注意建立数学模型,培养自己利用数学知识解决实际问题的能力.
18.【答案】解:根据题意得,,
当时,有最大值,的最大值为,
当长为时,花圃面积最大,最大面积为
【解析】根据题意得,,进而求解.
本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.
19.【答案】解:设每箱售价为元,销售总利润为元,
售价为元时,可销售箱;售价每提高元,销售量将减少箱,
销售量箱,
,
,图象开口向下,
当时,有最大值,最大值为,
答:当每箱售价为元时,销售利润最大,最大为元.
【解析】先根据题意求出销售量,然后写出与之间的函数关系式,配成顶点式,即可求出利润的最大值.
本题考查的是二次函数的应用,解题关键是掌握二次函数顶点式的配法.
20.【答案】解:根据题意得,;
根据题意得,,
解得:,,
每件利润不能超过元,
,
答:当为时,超市每天销售这种玩具可获利润元;
根据题意得,,
,
当时,随的增大而增大,且每件利润不能超过元,
当时,,
答:当为时最大,最大值是元.
【解析】本题考查了一元二次方程的应用、二次函数的应用,弄清题目中包含的数量关系是解题关键.
根据题意列函数关系式即可;
根据题意列方程即可得到结论;
根据题意得到,根据二次函数的性质得到当时,随的增大而增大,于是得到结论.
21.【答案】解:设与之间的函数表达式为,将表中数据、代入得:
,解得:.
与之间的函数表达式为.
由题意得:,
整理得:,
解得,.
答:为保证某天获得元的销售利润,则该天的销售单价应定为元千克或元千克.
设当天的销售利润为元,则:
,
,
当时,.
答:当销售单价定为元千克时,才能使当天的销售利润最大,最大利润是元.
【解析】本题考查了待定系数法求一次函数的解析式、一元二次方程和二次函数在实际问题中的应用,理清题中的数量关系是解题的关键.
利用待定系数法来求一次函数的解析式即可;
依题意可列出关于销售单价的方程,然后解一元二次方程即可;
利用每千克的利润乘以销售量可得总利润,然后根据二次函数的性质来进行计算即可.
22.【答案】解:
的最大值为
铅球在行进中的最大高度为.
令得:
解方程得,,负值舍去,
该男生把铅球推出的水平距离是 .
【解析】将所给二次函数写成顶点式,则顶点纵坐标即为所求的最大高度;
令得:,解方程,保留正值,即为该男生将铅球推出的距离.
本题考查了二次函数在实际问题中的应用,可以用配方法写成顶点式求得;同时本题还考查了二次函数与一元二次方程的关系及解一元二次方程,本题属于中档题.
23.【答案】解:设一次函数关系式为,
由图象可得,当时,;时,,
,解得.
与之间的关系式为.
设该公司日获利为元,由题意得,
,
抛物线开口向下;
对称轴,
当时,随着的增大而增大;
,
时,有最大值;.
即销售单价为每千克元时,日获利最大,最大获利为元.
【解析】通过题意,确定出二次函数的解析式即可;
利用二次函数解决利润问题,然后确定其最大值,实际问题中自变量的取值要使实际问题有意义.
本题考查了二次函数的应用,在商品经营活动中,经常会遇到求最大利润,最大销量等问题.
解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量的取值范围.
24.【答案】解:如图所示.
依题意,抛物线的顶点的坐标为,点的坐标为.
设该抛物线的表达式为,
由抛物线过点,
,
解得,
该抛物线的表达式为;
令,得.
解得,在正半轴,故舍去.
点的坐标为,
,
由,可得.
小明此次试投的成绩达到优秀.
【解析】本题是二次函数的应用,属于常考题型,此类题的解题思路为:先根据已知确定其顶点和与轴交点或轴交点,求解析式;根据图形中的某点坐标得出相应的结论.
根据题意画出铅球运动路径的示意图即可;
根据题意知抛物线的顶点是点,设出抛物线的顶点式,然后根据抛物线过点,可以求得抛物线的解析式;
令,求出点的坐标,即可得的长度,据此判断即可.
25.【答案】解:由题意得:
,
答:商家每天的利润元与降价元之间的函数关系为;
由得:,
,
时,最大为,
即当降价元时,商家每天的利润最大,最大为元;
,
解得:,,
,,
定价应为元之间.
【解析】此题考查二次函数的实际运用,解题的关键是求得函数解析式,进一步利用函数的性质解决问题.
根据利润销售量单价成本,列出函数关系式即可求解;
根据求得的函数关系式进一步利用配方法求出答案即可;
首先由中的函数得出降价元时,每天要获得元的利润,列方程,求出,进一步可得出答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.5用二次函数解决问题苏科版初中数学九年级下册同步练习
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
1.如图,正方形的边长为,点和点分别从点和点出发,沿射线向右运动,且速度相同,过点作,垂足为,连接,设点运动的距离为,的面积为,则能反映与之间的函数关系的图象大致为
( )
A. B.
C. D.
2.如图,正方形的边长为,点和点分别从点和点出发,沿射线向右运动,且速度相同,过点作,垂足为,连接,设点运动的距离为,的面积为,则能反映与之间的函数关系的图象大致为
A. B.
C. D.
3.服装店将进价为每件元的服装按每件元出售,每天可销售件,若想获得最大利润,则应定为( )
A. 元 B. 元 C. 元 D. 元
4.某商场销售的某种商品每件的标价是元,若按标价的八折销售,仍可盈利元,市场调查发现:在以标价打八折为销售价的基础上,该种商品每星期可卖出件,该种向品每降价元,每星期可多卖件设每件商品降价元为整数,每星期的利润为元以下说法错误的是( )
A. 每件商品进价为元
B. 降价后每件商品售价为元
C. 降价后每周可卖件
D. 每星期的利润为
5.心理学家发现:课堂上,学生对概念的接受能力与提出概念的时间单位:之间近似满足函数关系,值越大,表示接受能力越强.如图记录了学生学习某概念时与的三组数据,根据上述函数模型和数据,可推断出当学生接受能力最强时,提出概念的时间为
( )
A. B. C. D.
6.一个弹性球从地面竖直向上弹起时的速度为米秒,经过秒时,球距离地面的高度米满足公式,那么球弹起后又回到地面所花的时间是( )
A. B. C. D.
7.某水利工程公司开挖的沟渠,蓄水之后截面呈抛物线形,在图中建立平面直角坐标系,并标出相关数据单位:某学习小组探究之后得出如下结论,其中正确的为( )
A.
B. 池底所在抛物线的解析式为
C. 池塘最深处到水面的距离为
D. 若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的
8.如图,从地面竖直向上抛出一个小球,小球的高度与小球运动时间之间的表达式为,那么小球从抛出至落回到地面所需要的时间是( )
A. B. C. D.
9.在某市治理违建的过程中,某小区拆除了自建房,改建绿地如图,自建房占地是边长为的正方形,改建的绿地的是矩形,其中点在上,点在的延长线上,且那么当为多少时,绿地的面积最大?( )
A.
B.
C.
D.
10.如图,一座拱桥的轮廓是抛物线型,拱高,跨度,相邻两支柱间的距离均为,请根据所给的数据,则支柱的长度为( )
A. B. C. D.
11.如图,以的速度将小球沿与地面成角的方向击出时,小球的飞行路线将是一条抛物线如果不考虑空气阻力,小球的飞行高度单位:与飞行时间单位:之间具有函数关系下列叙述正确的是( )
A. 小球的飞行高度只有在时达到 B. 小球的飞行高度可以达到
C. 小球从飞出到落地要用时 D. 小球飞出时的飞行高度为
12.一个直角三角形的两条直角边长的和为,其中一条直角边长为,三角形的面积为,则与之间的函数解析式为
.( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
13.如图,一位篮球运动员投篮,球沿抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为,则他距篮筐中心的水平距离是
14.如图,某中学综合与实践小组要围成一个矩形菜园,其中一边靠墙,其余的三边,,用总长为米的栅栏围成.设矩形的边米,面积为平方米.
活动区面积与之间的关系式为 ;
菜园最大面积是 平方米.
15.飞机着陆后滑行的距离单位:关于滑行时间单位:的函数解析式是在飞机着陆滑行中,最后滑行的距离是____.
16.某抛物线形隧道的最大高度为米,跨度为米,按如图所示的方式建立平面直角坐标系,它对应的表达式为______ .
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高,与篮圈中心的水平距离为,当球出手后水平距离为时到达最大高度,设篮球运动的轨迹为抛物线,篮圈距地面建立如图所示的平面坐标系,求抛物线的解析式并判断此球能否准确投中?
18.本小题分
如图,用一段长为的篱笆围成一个一边靠墙的矩形花圃,墙长设长为,矩形的面积为问:当长为多少米时,所围成的花圃面积最大?最大面积是多少?
19.本小题分
商场销售某品牌牛奶,已知进价为每箱元经市场调研,售价为元时,可销售箱;售价每提高元,销售量将减少箱当每箱售价为多少元时,才能使利润最大?最大利润是多少元?
20.本小题分
超市销售某种儿童玩具,如果每件利润为元市场管理部门规定,该种玩具每件利润不能超过元,每天可售出件.根据市场调查发现,销售单价每增加元,每天销售量会减少件.设销售单价增加元,每天售出件.
请写出与之间的函数表达式;
当为多少时,超市每天销售这种玩具可获利润元?
设超市每天销售这种玩具可获利元,当为多少时,最大,最大值是多少?
21.本小题分
某超市经销一种商品,每千克成本为元,经试销发现,该种商品的每天销售量千克与销售单价元千克满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
销售单价元千克
销售量千克
求千克与元千克之间的函数表达式;
为保证某天获得元的销售利润,则该天的销售单价应定为多少?
当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?
22.本小题分
如图,一名男生推铅球,铅球行进高度单位:与水平距离单位:之间的关系是.
求:
铅球在行进中的最大高度;
该男生将铅球推出的距离是多少?
23.本小题分
我市某化工材料经销商购进一种化工材料若干千克,成本为每千克元,物价部门规定其销售单价不低于成本价且不高于成本价的倍,经试销发现,日销售量千克与销售单价元符合一次函数关系,如图所示.
求与之间的函数关系式,并写出自变量的取值范围;
若在销售过程中每天还要支付其他费用元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?
24.本小题分
小明进行铅球训练,他尝试利用数学模型来研究铅球的运动情况.他以水平方向为轴方向,为单位长度,建立了如图所示的平面直角坐标系,铅球从轴上的点出手,运动路径可看作抛物线,在点处达到最高位置,落在轴上的点处.小明某次试投时的数据如图所示.
在图中画出铅球运动路径的示意图;
根据图中信息,求出铅球路径所在抛物线的表达式;
若铅球投掷距离铅球落地点与出手点的水平距离的长度不小于,成绩为优秀.请通过计算,判断小明此次试投的成绩是否能达到优秀.
25.本小题分
蚌埠,古乃采珠之地,素有“珍珠城”之美誉,已知一批珍珠每颗的进价为元,售价定为元颗时,每天可销售颗,为扩大市场占有率,商家决定采取适当的降价措施,经调查发现,售价每降低元,每天销量可增加颗销售单价不低于进价.
写出商家每天的利润元与降价元之间的函数关系
当降价多少元时,商家每天的利润最大,最大利润是多少
若商家每天的利润至少要达到元,则定价应在什么范围内
答案和解析
1.【答案】
【解析】解:过点作,垂足为.
是正方形的对角线
是等腰直角三角形
的面积
与之间的函数关系是二次函数,且二次函数图象开口方向向上;
因此,选项中只有选项符合条件.
故选:.
根据正方形的性质得到,由题意得出是等腰直角三角形;过点作的高,同时也是的高;再根据等腰直角三角形的性质求出,也就能求出的面积了.
此题综合性较强,涉及二次函数、等腰三角形等知识,是近年来较为流行的试题,解题的关键在于结合题目的要求动中取静,相信解决这种问题不会非常难.
2.【答案】
【解析】解:过点作,垂足为.
是正方形的对角线
是等腰直角三角形
的面积
与之间的函数关系是二次函数,且二次函数图象开口方向向上;
因此,选项中只有选项符合条件.
故选:.
根据正方形的性质得到,由题意得出是等腰直角三角形;过点作的高,同时也是的高;再根据等腰直角三角形的性质求出,也就能求出的面积了.
此题综合性较强,涉及二次函数、等腰三角形等知识,是近年来较为流行的试题,解题的关键在于结合题目的要求动中取静,相信解决这种问题不会非常难.
3.【答案】
【解析】【分析】
本题考查了二次函数在实际问题中的应用,正确地写出函数关系式,并明确二次函数的性质,是解题的关键.设获得的利润为元,由题意得关于的二次函数,配方,写成顶点式,利用二次函数的性质可得答案.
【解答】
解:设获得的利润为元,由题意得:
,,
当时,取得最大值元.
故选A.
4.【答案】
【解析】解:由题意,设每件商品进价为元,
.
,即可判断A正确,不符合题意.
此时降价后每件商品售价为:,即可判断B正确,不符合题意.
降价后每周可卖件,可以判断C正确,不符合题意.
由上,每星期的利润为,即可判断D错误,符合题意.
故选:.
依据题意,设每件商品进价为元,由,即可判断;降价后每件商品售价为:,即可判断;降价后每周可卖件,可以判断;由上,每星期的利润为,即可判断.
本题主要考查二次函数的应用,解题的关键是理解题意找到其蕴含的相等关系,并据此列出函数解析式,也要求熟练掌握二次函数的性质.
5.【答案】
【解析】【分析】
本题考查了二次函数的性质在实际生活中的应用,首先要吃透题意,确定已知点坐标,求出函数表达式,通常自变量在对称轴时,函数取得最值.
把点坐标:、、,代入函数,求出函数表达式,由,故函数有最大值,即:当时,有最大值.
【解答】
解:由题意得:函数过点、、,
把以上三点坐标代入得:
,解得:,
则函数的表达式为:,
,则函数有最大值,
当时,有最大值,即学生接受能力最强,
故选:.
6.【答案】
【解析】解:令,得:,
解得:或,
那么球弹起后又回到地面所花的时间是秒;
故选:.
根据二次函数的性质即可得到结论.
本题主要考查二次函数的应用,熟练掌握二次函数的图象和性质是解题的关键.
7.【答案】
【解析】解:设池底所在抛物线的解析式为,
把抛物线上点,,,代入抛物线解析式中得:
,
解得:,
解析式为.
选项A中,,故选项A错误,该选项不符合题意;
选项B中,池底所在抛物线的解析式为,故选项B错误,该选项不符合题意;
选项C中,池塘水深最深处为点,水面为,,
,
所以水深最深处为点到水面的距离为,故选项C正确,该选项符合题意;
选项D中,若池塘中水面的宽度由原来的减少到原来的一半为,
由抛物线关于轴对称可知,抛物线上点横坐标,代入解析式算得,
即最深处到水面的距离为米,
而原来最深处到水面的距离为米,减少为原来的故选项D错误,该选项不符合题意.
故选:.
利用建立的坐标系得到抛物线上点的坐标,然后通过待定系数法求出抛物线解析式,根据二次函数的性质对照选项逐一判定即可.
本题考查二次函数的实际应用问题,计算较为复杂,在计算时需要理清楚实际数据在坐标系中对应的位置.能够正确计算和分析实际情况是解题的关键.
8.【答案】
【解析】解:由小球高度与运动时间的关系式.
令,
解得:不合题意,舍去,
,小球从抛出至回落到地面所需要的时间是秒.
故选:.
由小球高度与运动时间的关系式,令,解得的两值之差便是所要求得的结果.
本题考查了运动函数方程,是二次函数的实际应用.
9.【答案】
【解析】解:设,则,绿地的面积为,根据题意得:
.
二次项系数为,
当时,有最大值.
即当时,绿地面积最大.
故选:.
依据题意,设,则,绿地的面积为,根据题意得关于的二次函数,然后写成顶点式,利用二次函数的性质可得答案.
本题考查了二次函数在几何图形问题中的应用,根据题意正确得出所求的面积关于的函数关系式、明确二次函数的相关性质是解题的关键.
10.【答案】
【解析】解:如图所示,建立平面直角坐标系,
由题意得点坐标,点坐标为,点坐标为,点横坐标为,
设抛物线解析式为,
,
,
抛物线解析式为,
当时,,
支柱的高度,
故选:.
如图所示,建立坐标系,然后求出抛物线解析式,然后求出点纵坐标,即可求解.
本题主要考查了二次函数的应用,解题的关键在于能够根据题意正确建立坐标系求解.
11.【答案】
【解析】解:、当时,,
解得:,,
故当或小球的飞行高度能达到,故此选项错误,不符合题意;
B、,
故时,小球的飞行高度最大为:,故此选项错误,不符合题意;
C、时,,
解得:,,
小球从飞出到落地要用时,故此选项错误,不符合题意;
D、由题意,当时,,
故小球飞出时的飞行高度为,故此选项正确,符合题意;
故选:.
依据题意,根据二次函数的性质逐项进行判断即可得解.
本题主要考查了二次函数的应用,正确解方程是解题关键.
12.【答案】
【解析】解:直角三角形的两条直角边的和等于,且它的一条直角边为,
另一条直角边为,
直角三角形的面积,
与之间的函数关系式.
本题考查了二次函数的应用,根据各数量之间的关系,找出与之间的函数关系式是解题的关键.
13.【答案】
【解析】【分析】
此题考查二次函数的运用,根据所建坐标系确定水平距离的求法是此题关键.根据所建坐标系,水平距离就是时离他最远的距离.
【解答】
解:当时,,
,
,
解得:,,
故他距篮筐中心的水平距离是.
故答案为.
14.【答案】
【解析】【分析】本题考查二次函数的应用,
表示出 ,由矩形面积公式可得函数关系式;
把面积配成顶点式,由二次函数性质可得答案.
【详解】解:由题意得: ,
,
,解得 ,
活动区面积与 之间的关系式为 ;
解:由得:活动区面积与 之间的关系式为 ,
,
当 时,取最大值,
菜园 最大面积是平方米;
15.【答案】
【解析】解:当取得最大值时,飞机停下来,
,
即当时,飞机滑行才停下来,
当时,,
,
故答案为.
当取得最大值时,飞机停下来,,即当时,飞机滑行才停下来,当时,,即可求解.
本题考查了二次函数的性质在实际生活中的应用,本题要首先确定飞机最大滑行时间,然后确定最后秒滑行的距离.
16.【答案】
【解析】解:由题意知,抛物线的顶点坐标为,过,
设抛物线对应的表达式为,
将代入得,,
解得,,
,
故答案为:.
由题意知,抛物线的顶点坐标为,过,设抛物线对应的表达式为,将代入得,,解得,,进而可得结果.
本题考查二次函数的应用,解题的关键是灵活应用抛物线的顶点式解决问题,属于中考常考题型.
17.【答案】解:由题意得,抛物线的顶点坐标为,球出手时的坐标为,
设抛物线解析式为:,
将点代入可得:,
解得:,
则抛物线的解析式为:
令,则,
,
此球能准确投中.
【解析】根据抛物线的顶点坐标及球出手时的坐标,可确定抛物线的解析式,令,求出的值,与比较即可作出判断.
本题考查了二次函数的应用,解答本题的关键是利用待定系数法求出抛物线解析式,注意建立数学模型,培养自己利用数学知识解决实际问题的能力.
18.【答案】解:根据题意得,,
当时,有最大值,的最大值为,
当长为时,花圃面积最大,最大面积为
【解析】根据题意得,,进而求解.
本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.
19.【答案】解:设每箱售价为元,销售总利润为元,
售价为元时,可销售箱;售价每提高元,销售量将减少箱,
销售量箱,
,
,图象开口向下,
当时,有最大值,最大值为,
答:当每箱售价为元时,销售利润最大,最大为元.
【解析】先根据题意求出销售量,然后写出与之间的函数关系式,配成顶点式,即可求出利润的最大值.
本题考查的是二次函数的应用,解题关键是掌握二次函数顶点式的配法.
20.【答案】解:根据题意得,;
根据题意得,,
解得:,,
每件利润不能超过元,
,
答:当为时,超市每天销售这种玩具可获利润元;
根据题意得,,
,
当时,随的增大而增大,且每件利润不能超过元,
当时,,
答:当为时最大,最大值是元.
【解析】本题考查了一元二次方程的应用、二次函数的应用,弄清题目中包含的数量关系是解题关键.
根据题意列函数关系式即可;
根据题意列方程即可得到结论;
根据题意得到,根据二次函数的性质得到当时,随的增大而增大,于是得到结论.
21.【答案】解:设与之间的函数表达式为,将表中数据、代入得:
,解得:.
与之间的函数表达式为.
由题意得:,
整理得:,
解得,.
答:为保证某天获得元的销售利润,则该天的销售单价应定为元千克或元千克.
设当天的销售利润为元,则:
,
,
当时,.
答:当销售单价定为元千克时,才能使当天的销售利润最大,最大利润是元.
【解析】本题考查了待定系数法求一次函数的解析式、一元二次方程和二次函数在实际问题中的应用,理清题中的数量关系是解题的关键.
利用待定系数法来求一次函数的解析式即可;
依题意可列出关于销售单价的方程,然后解一元二次方程即可;
利用每千克的利润乘以销售量可得总利润,然后根据二次函数的性质来进行计算即可.
22.【答案】解:
的最大值为
铅球在行进中的最大高度为.
令得:
解方程得,,负值舍去,
该男生把铅球推出的水平距离是 .
【解析】将所给二次函数写成顶点式,则顶点纵坐标即为所求的最大高度;
令得:,解方程,保留正值,即为该男生将铅球推出的距离.
本题考查了二次函数在实际问题中的应用,可以用配方法写成顶点式求得;同时本题还考查了二次函数与一元二次方程的关系及解一元二次方程,本题属于中档题.
23.【答案】解:设一次函数关系式为,
由图象可得,当时,;时,,
,解得.
与之间的关系式为.
设该公司日获利为元,由题意得,
,
抛物线开口向下;
对称轴,
当时,随着的增大而增大;
,
时,有最大值;.
即销售单价为每千克元时,日获利最大,最大获利为元.
【解析】通过题意,确定出二次函数的解析式即可;
利用二次函数解决利润问题,然后确定其最大值,实际问题中自变量的取值要使实际问题有意义.
本题考查了二次函数的应用,在商品经营活动中,经常会遇到求最大利润,最大销量等问题.
解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量的取值范围.
24.【答案】解:如图所示.
依题意,抛物线的顶点的坐标为,点的坐标为.
设该抛物线的表达式为,
由抛物线过点,
,
解得,
该抛物线的表达式为;
令,得.
解得,在正半轴,故舍去.
点的坐标为,
,
由,可得.
小明此次试投的成绩达到优秀.
【解析】本题是二次函数的应用,属于常考题型,此类题的解题思路为:先根据已知确定其顶点和与轴交点或轴交点,求解析式;根据图形中的某点坐标得出相应的结论.
根据题意画出铅球运动路径的示意图即可;
根据题意知抛物线的顶点是点,设出抛物线的顶点式,然后根据抛物线过点,可以求得抛物线的解析式;
令,求出点的坐标,即可得的长度,据此判断即可.
25.【答案】解:由题意得:
,
答:商家每天的利润元与降价元之间的函数关系为;
由得:,
,
时,最大为,
即当降价元时,商家每天的利润最大,最大为元;
,
解得:,,
,,
定价应为元之间.
【解析】此题考查二次函数的实际运用,解题的关键是求得函数解析式,进一步利用函数的性质解决问题.
根据利润销售量单价成本,列出函数关系式即可求解;
根据求得的函数关系式进一步利用配方法求出答案即可;
首先由中的函数得出降价元时,每天要获得元的利润,列方程,求出,进一步可得出答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
