5.3.1平行线的性质课件
文档属性
| 名称 | 5.3.1平行线的性质课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 512.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-29 00:00:00 | ||
图片预览


文档简介
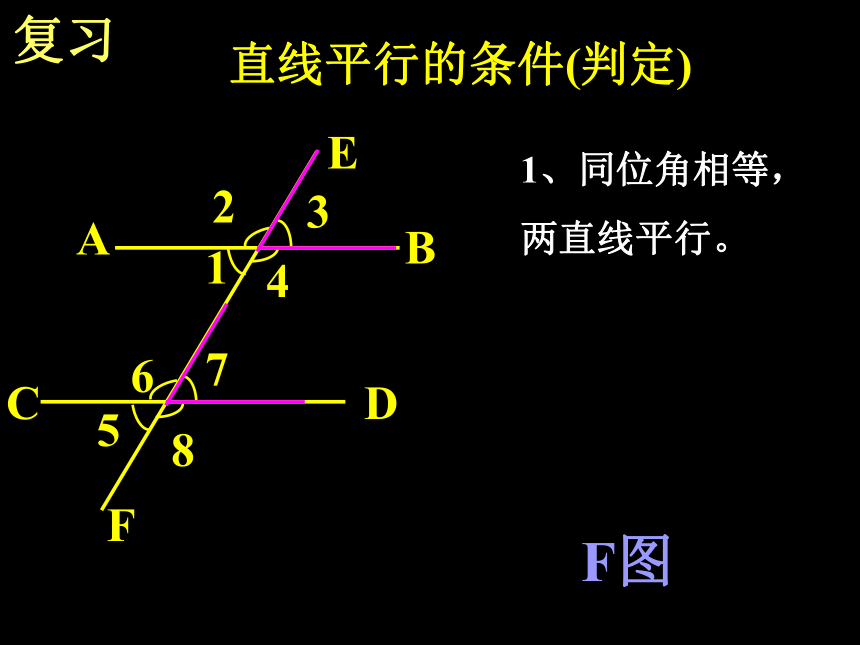
课件27张PPT。平行线的性质(一)第五章 相交线与平行线复习CDABEF85612347直线平行的条件(判定)1、同位角相等,
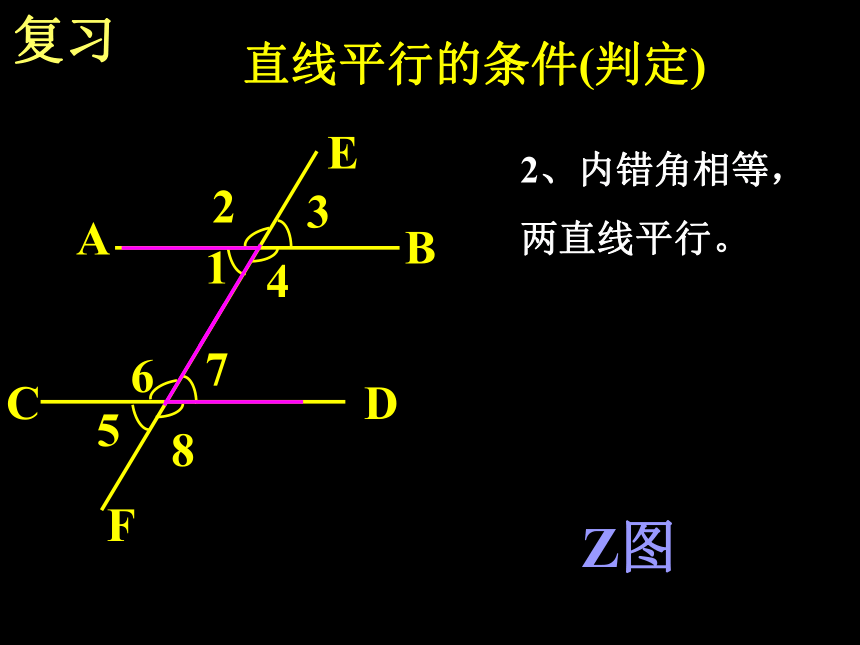
两直线平行。F图复习CDABE85612347直线平行的条件(判定)2、内错角相等,
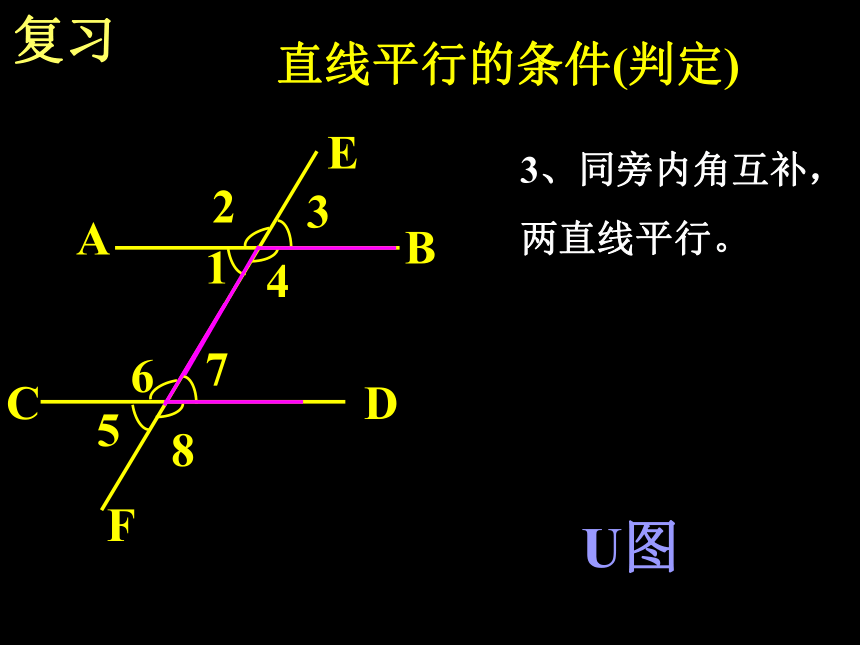
两直线平行。Z图F复习CDABE85612347直线平行的条件(判定)3、同旁内角互补,
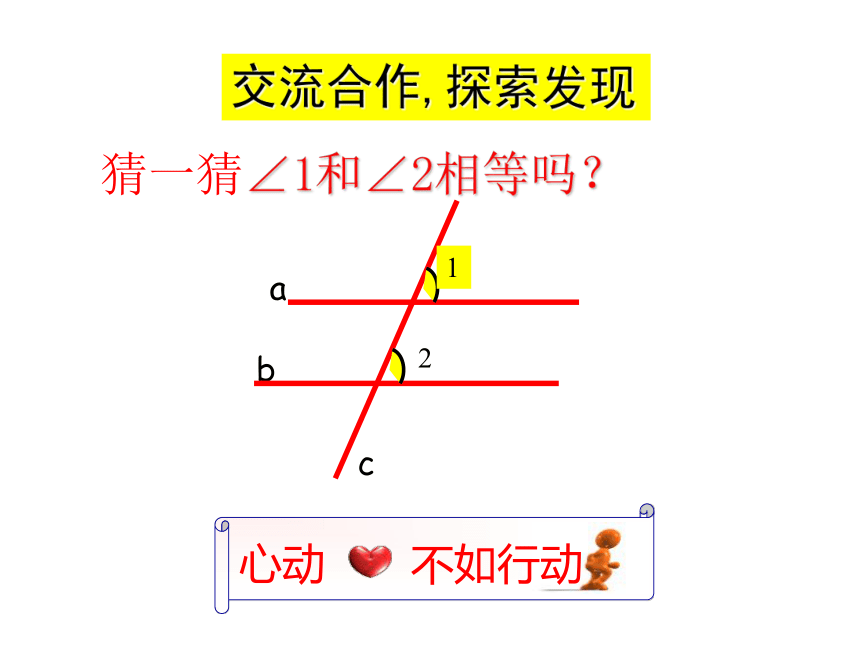
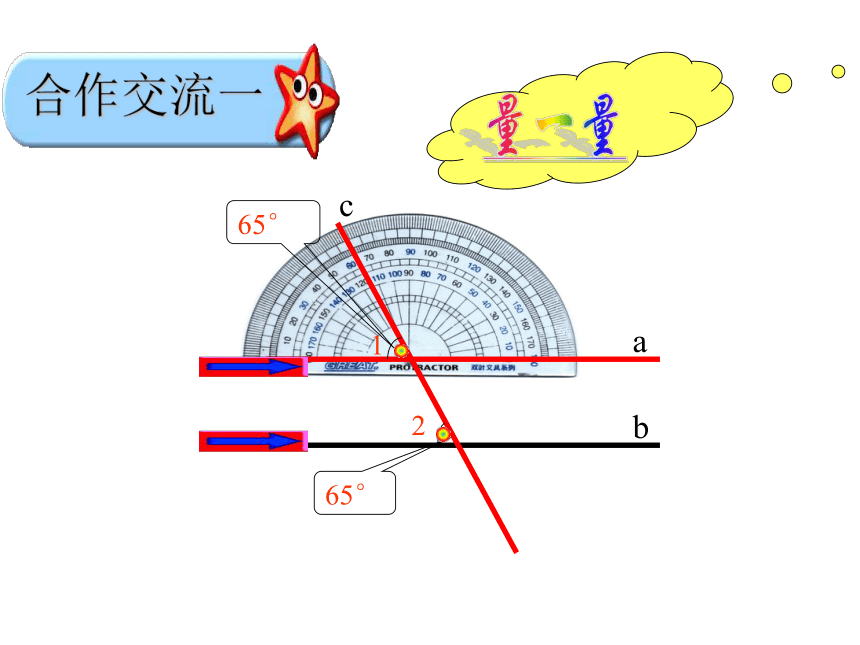
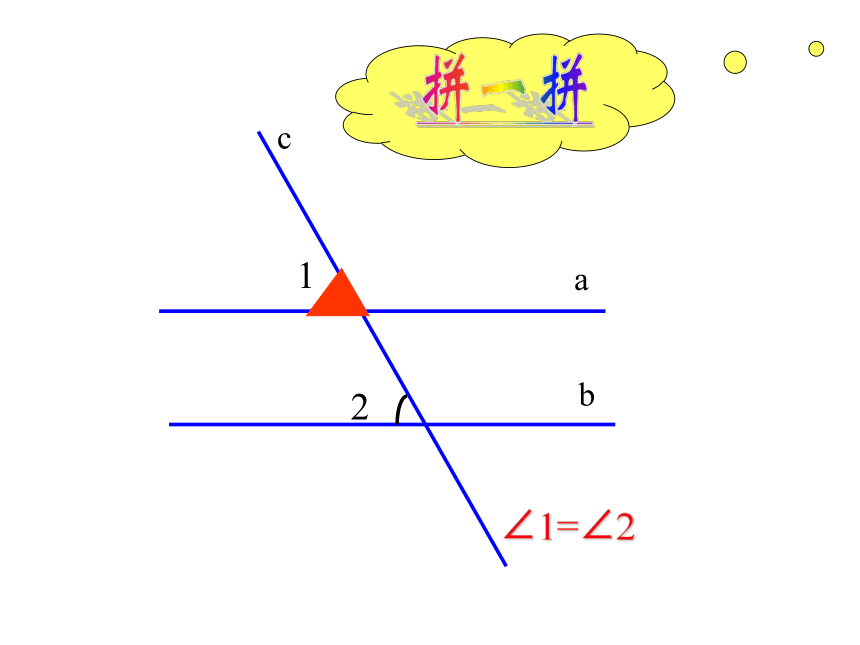
两直线平行。U图F猜一猜∠1和∠2相等吗?交流合作,探索发现65°65°cab12合作交流一ac1∠1=∠2 是不是任意一条直线去截平行线a、b
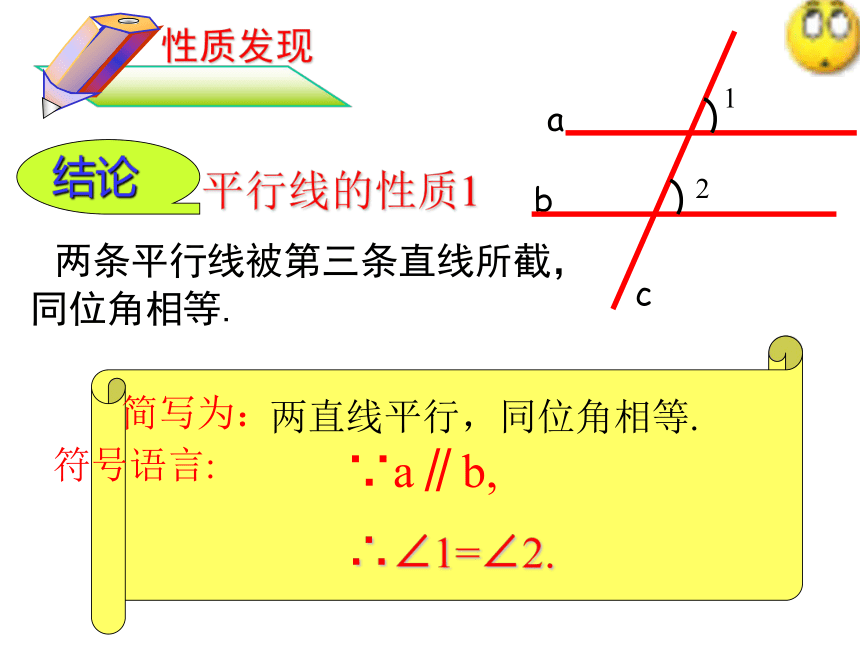
所得的同位角都相等呢?两直线平行,同位角相等.平行线的性质1结论 两条平行线被第三条直线所截,
同位角相等.∴∠1=∠2.∵a∥b,简写为:符号语言: 如图:已知a//b,那么?2与?3相等吗?
为什么?解∵a∥b(已知),
∴∠1=∠2(两直线平行,
同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).合作交流二两直线平行,内错角相等.平行线的性质2结论 两条平行线被第三条直线所截,
内错角相等.∴∠2=∠3.∵a∥b,符号语言:简写为:解: ∵a//b (已知), 如图,已知a//b,那么?2与?4有什么关系呢?为什么?合作交流三∴? 1= ? 2(两直线平行, 同位角相等). ∵ ? 1+ ? 4=180° (邻补角定义), ∴? 2+ ? 4=180° (等量代换).两直线平行,同旁内角互补.平行线的性质3结论 两条平行线被第三条直线所截,
同旁内角互补.∴? 2+ ? 4=180°.∵a∥b,符号语言:简写为:练习1、如图,直线 a∥b ,∠1=54°,那么
∠ 2、 ∠ 3、 ∠ 4各是多少度?bac1234范例例1 如图是一块梯形铁片的残余部分,
量得∠A=100°, ∠B=115 ° ,梯形
另外两个角分别是多少度?DCAB巩固ABCD2、如图,
若 AD∥BC ,则
∠ = ∠ ,
∠ = ∠ ,∠ABC+ ∠ =180°;
若DC∥AB,则
∠ = ∠ , ∠ = ∠ ,
∠ABC+ ∠ =180°;练习3、如图, AB∥EF, CD∥EF ,∠B=40°、∠D=35 °,求∠BED的大小。类比“直线平行的条件(判定)”与“平行线的性质”条件(判定)性质1、同位角相等,
两直线平行1、两直线平行,
同位角相等2、内错角相等,
两直线平行2、两直线平行,
内错角相等3、同旁内角互补,
两直线平行3、两直线平行,
同旁内角互补类比直线平行的
条件(判定)平行线的
性质由角的大小关系转化为直线的位置关系由直线的位置关系转化为角的大小关系范例例2、如图, AB∥DC ,GM、HN分别是
∠ BGH 、∠DHF的平分线,GM、HN有
什么关系?为什么?练习2、如图, AB∥DC ,GM、HN分别是
∠AGH 、∠ GHD的平分线,GM、HN有
什么关系?为什么?复习回顾平行线的判定方法是什么?反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢? 例 如图,已知直线a∥b,
∠1 = 500, 求∠2的度数.abc12∴∠ 2= 500 (等量代换).解:∵ a∥b(已知),∴∠ 1= ∠ 2
(两直线平行,内错角相等).又∵∠ 1 = 500 (已知),变式1:已知条件不变,求∠3,∠4的度数? 师生互动,典例示范变式2:已知∠3 =∠4,∠1=47°,求∠2的度数?∴∠ 2= 470
( )解:∵ ∠3 =∠4( )∴a∥b
( )
又∵∠ 1 = 470 ( )c1234abd 如图在四边形ABCD中,已知AB∥CD,
∠B = 600.
①求∠C的度数;
②由已知条件能否求得∠A的度数?ABCD解: ① ∵ AB∥CD(已知),
∴ ∠B + ∠C= 1800(两直线平行,同旁内角互补).
又∵ ∠B = 600 (已知),
∴∠C = 1200 (等式的性质).②根据题目的已知条件,
无法求出∠A的度数. 如图,在汶川大地震当中,一辆抗震救灾汽车经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1420,第二次拐的角∠C是多少度?为什么?解:∵AB∥CD (已知),∴∠B=∠C(两直线平行,
内错角相等).又∵∠B=142° (已知),∴∠B=∠C=142°(等量代换).小结1、本节课你学到了什么知识?2、你还学到了什么数学思想?平行线的性质转化的数学思想
两直线平行。F图复习CDABE85612347直线平行的条件(判定)2、内错角相等,
两直线平行。Z图F复习CDABE85612347直线平行的条件(判定)3、同旁内角互补,
两直线平行。U图F猜一猜∠1和∠2相等吗?交流合作,探索发现65°65°cab12合作交流一ac1∠1=∠2 是不是任意一条直线去截平行线a、b
所得的同位角都相等呢?两直线平行,同位角相等.平行线的性质1结论 两条平行线被第三条直线所截,
同位角相等.∴∠1=∠2.∵a∥b,简写为:符号语言: 如图:已知a//b,那么?2与?3相等吗?
为什么?解∵a∥b(已知),
∴∠1=∠2(两直线平行,
同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).合作交流二两直线平行,内错角相等.平行线的性质2结论 两条平行线被第三条直线所截,
内错角相等.∴∠2=∠3.∵a∥b,符号语言:简写为:解: ∵a//b (已知), 如图,已知a//b,那么?2与?4有什么关系呢?为什么?合作交流三∴? 1= ? 2(两直线平行, 同位角相等). ∵ ? 1+ ? 4=180° (邻补角定义), ∴? 2+ ? 4=180° (等量代换).两直线平行,同旁内角互补.平行线的性质3结论 两条平行线被第三条直线所截,
同旁内角互补.∴? 2+ ? 4=180°.∵a∥b,符号语言:简写为:练习1、如图,直线 a∥b ,∠1=54°,那么
∠ 2、 ∠ 3、 ∠ 4各是多少度?bac1234范例例1 如图是一块梯形铁片的残余部分,
量得∠A=100°, ∠B=115 ° ,梯形
另外两个角分别是多少度?DCAB巩固ABCD2、如图,
若 AD∥BC ,则
∠ = ∠ ,
∠ = ∠ ,∠ABC+ ∠ =180°;
若DC∥AB,则
∠ = ∠ , ∠ = ∠ ,
∠ABC+ ∠ =180°;练习3、如图, AB∥EF, CD∥EF ,∠B=40°、∠D=35 °,求∠BED的大小。类比“直线平行的条件(判定)”与“平行线的性质”条件(判定)性质1、同位角相等,
两直线平行1、两直线平行,
同位角相等2、内错角相等,
两直线平行2、两直线平行,
内错角相等3、同旁内角互补,
两直线平行3、两直线平行,
同旁内角互补类比直线平行的
条件(判定)平行线的
性质由角的大小关系转化为直线的位置关系由直线的位置关系转化为角的大小关系范例例2、如图, AB∥DC ,GM、HN分别是
∠ BGH 、∠DHF的平分线,GM、HN有
什么关系?为什么?练习2、如图, AB∥DC ,GM、HN分别是
∠AGH 、∠ GHD的平分线,GM、HN有
什么关系?为什么?复习回顾平行线的判定方法是什么?反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢? 例 如图,已知直线a∥b,
∠1 = 500, 求∠2的度数.abc12∴∠ 2= 500 (等量代换).解:∵ a∥b(已知),∴∠ 1= ∠ 2
(两直线平行,内错角相等).又∵∠ 1 = 500 (已知),变式1:已知条件不变,求∠3,∠4的度数? 师生互动,典例示范变式2:已知∠3 =∠4,∠1=47°,求∠2的度数?∴∠ 2= 470
( )解:∵ ∠3 =∠4( )∴a∥b
( )
又∵∠ 1 = 470 ( )c1234abd 如图在四边形ABCD中,已知AB∥CD,
∠B = 600.
①求∠C的度数;
②由已知条件能否求得∠A的度数?ABCD解: ① ∵ AB∥CD(已知),
∴ ∠B + ∠C= 1800(两直线平行,同旁内角互补).
又∵ ∠B = 600 (已知),
∴∠C = 1200 (等式的性质).②根据题目的已知条件,
无法求出∠A的度数. 如图,在汶川大地震当中,一辆抗震救灾汽车经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1420,第二次拐的角∠C是多少度?为什么?解:∵AB∥CD (已知),∴∠B=∠C(两直线平行,
内错角相等).又∵∠B=142° (已知),∴∠B=∠C=142°(等量代换).小结1、本节课你学到了什么知识?2、你还学到了什么数学思想?平行线的性质转化的数学思想
