第22章《相似形》单元检测题 (含答案) 九年级上册数学沪科版
文档属性
| 名称 | 第22章《相似形》单元检测题 (含答案) 九年级上册数学沪科版 |

|
|
| 格式 | docx | ||
| 文件大小 | 526.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-08 14:10:46 | ||
图片预览



文档简介
第22章《相似形》单元检测题
2023-2024学年九年级上册数学沪科版
一、单选题(本大题共12小题,每小题3分,共36分)
1.已知线段,,则,的比例中项线段等于( )
A.2 B.4 C.6 D.9
2.如图,在中,高相交于点,图中与相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在中,DE∥BC,若,则的值为( )
A. B. C. D.
4.如图,△ABC∽△ADE,若AB=9,AD=3,DE=2,则BC的长是( )
A.4 B.6 C.8 D.7
5.如图,四边形与四边形是位似图形,点O是位似中心.若,四边形的面积是25,则四边形的面积是( )
A.4 B.10 C. D.
6.如图,平行四边形中,的平分线分别与、交于点、.当,时,的值为( )
A. B. C. D.
7.如图,在两个等腰直角△ABC和△ADE中,∠DAE=∠BAC=90°,已知AC=5,AD=3,DE交AB于点P,当时,则S△AEP:S△BDP的值为( )
A. B. C. D.
8.如图,在平行四边形ABCD中,点F在CD边上,CF:DF=1:2,则S△CEF:S△AEB等于( )
A.1:2 B.1:3 C.1:4 D.1:9
9.如图,点D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为30,那么△ACD的面积为( )
A.5 B.7.5 C.10 D.15
10.已知的三边长分别为1,,,的两边长分别为和.若,则的第三边长为( )
A. B.2 C. D.
11.如果整张纸与半张纸相似,则整张纸的长和宽的比是( )
A. B. C. D.
12.如图,在矩形ABCD中,AB=3,BC=4,点E是边BC的中点,连接AE,与对角线BD交于点F.点M是AD边上的一个动点,连接MF、MC,则MF+MC的最小值为( )
A. B.4 C. D.5
二、填空题(本大题共8小题,每小题3分,共24分)
13.如图,在平面直角坐标系中,□AOBC的边AO在x轴上,经过点C的反比例函数交OB于点D,且OD=2BD,若□AOBC的面积是6,则k的值是 .
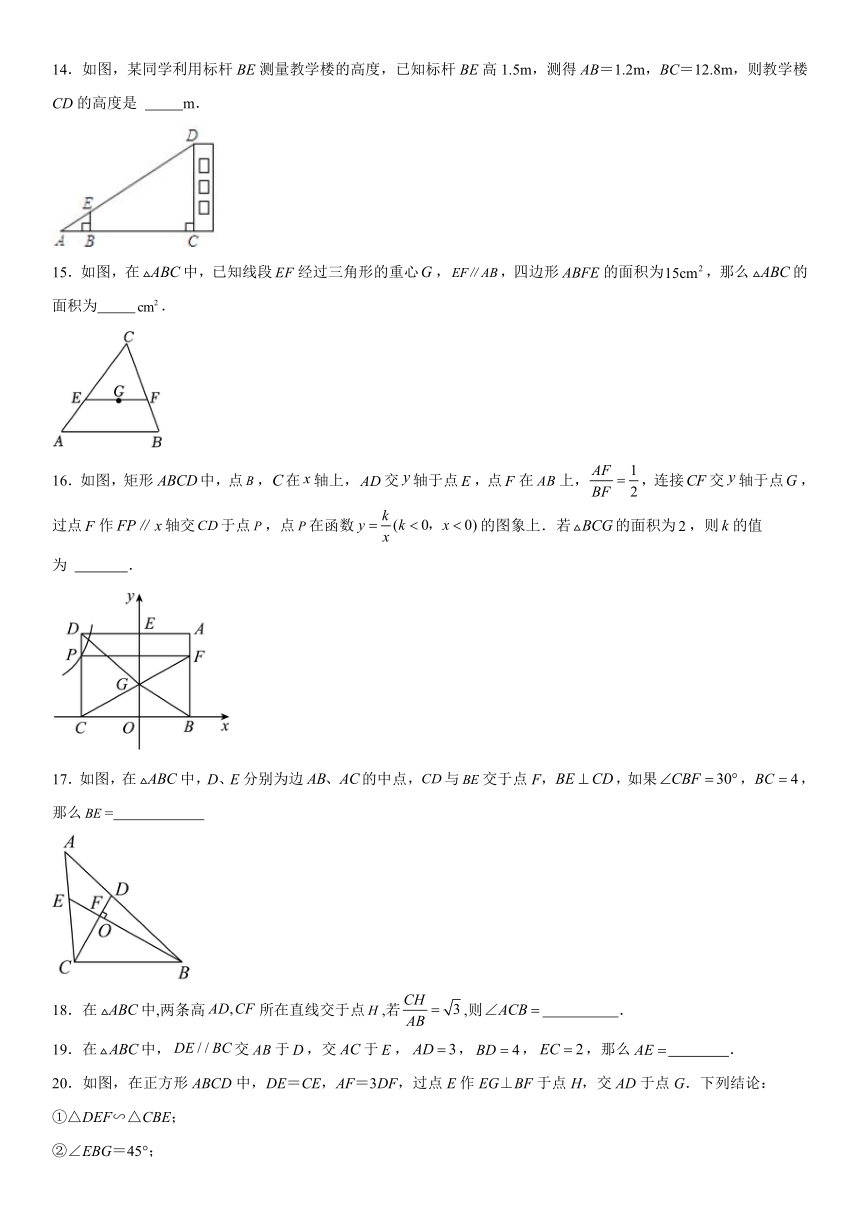
14.如图,某同学利用标杆BE测量教学楼的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则教学楼CD的高度是 m.
15.如图,在中,已知线段经过三角形的重心,,四边形的面积为,那么的面积为 .
16.如图,矩形中,点,在轴上,交轴于点,点在上,,连接交轴于点,过点作轴交于点,点在函数的图象上.若的面积为,则的值为 .
17.如图,在中,D、E分别为边的中点,与交于点F,,如果,,那么=
18.在中,两条高所在直线交于点,若,则 .
19.在中,交于,交于,,,,那么 .
20.如图,在正方形ABCD中,DE=CE,AF=3DF,过点E作EG⊥BF于点H,交AD于点G.下列结论:
①△DEF∽△CBE;
②∠EBG=45°;
③AD=3AG.正确的有 .
三、解答题(本大题共5小题,每小题8分,共40分)
21.如图,铁道口的栏杆短臂长1米,长臂长16米,当短臂的端点下降0.5米时,求长臂端点应升高了多少米?
22.如图,在中,点,,分别在边,和上,连接,,得到四边形是菱形,若,,,求菱形的面积.
23.已知=k,求k2-3k-4的值.
24.(1)如图,在中,,,点、分别在射线、上(点不与点、点重合),且保持.
①若点在线段上,且,求线段的长;
②若,,求与之间的函数关系式,并写出的取值范围;
(2)正方形的边长为5(如图),点、分别在直线、上(点不与点、点重合),且保持.当时,写出线段的长(不需要计算过程,请直接写出结果).
25.如图1,已知二次函数的图象过点,,且与y轴交于点.
(1)求此二次函数的表达式;
(2)点E在此抛物线的对称轴上,且,求点E的坐标;
(3)如图2,点Q为x轴下方抛物线上一动点,直线AQ,BQ分别交y轴于点M,N,试探究的积是否存在最大值?若存在,请求出最大值及点Q的坐标;若不存在,请说明理由.
参考答案:
1.C
2.C
3.D
4.B
5.A
6.B
7.D
8.D
9.C
10.B
11.B
12.C
13.
14.17.5
15.27
16.
17.
18.或
19.1.5
20.①②③
21.8.
22.
23.-或6.
24.(1)①;②; (2) 或或或
25.(1)
(2)或
(3)存在,12,
2023-2024学年九年级上册数学沪科版
一、单选题(本大题共12小题,每小题3分,共36分)
1.已知线段,,则,的比例中项线段等于( )
A.2 B.4 C.6 D.9
2.如图,在中,高相交于点,图中与相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在中,DE∥BC,若,则的值为( )
A. B. C. D.
4.如图,△ABC∽△ADE,若AB=9,AD=3,DE=2,则BC的长是( )
A.4 B.6 C.8 D.7
5.如图,四边形与四边形是位似图形,点O是位似中心.若,四边形的面积是25,则四边形的面积是( )
A.4 B.10 C. D.
6.如图,平行四边形中,的平分线分别与、交于点、.当,时,的值为( )
A. B. C. D.
7.如图,在两个等腰直角△ABC和△ADE中,∠DAE=∠BAC=90°,已知AC=5,AD=3,DE交AB于点P,当时,则S△AEP:S△BDP的值为( )
A. B. C. D.
8.如图,在平行四边形ABCD中,点F在CD边上,CF:DF=1:2,则S△CEF:S△AEB等于( )
A.1:2 B.1:3 C.1:4 D.1:9
9.如图,点D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为30,那么△ACD的面积为( )
A.5 B.7.5 C.10 D.15
10.已知的三边长分别为1,,,的两边长分别为和.若,则的第三边长为( )
A. B.2 C. D.
11.如果整张纸与半张纸相似,则整张纸的长和宽的比是( )
A. B. C. D.
12.如图,在矩形ABCD中,AB=3,BC=4,点E是边BC的中点,连接AE,与对角线BD交于点F.点M是AD边上的一个动点,连接MF、MC,则MF+MC的最小值为( )
A. B.4 C. D.5
二、填空题(本大题共8小题,每小题3分,共24分)
13.如图,在平面直角坐标系中,□AOBC的边AO在x轴上,经过点C的反比例函数交OB于点D,且OD=2BD,若□AOBC的面积是6,则k的值是 .
14.如图,某同学利用标杆BE测量教学楼的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则教学楼CD的高度是 m.
15.如图,在中,已知线段经过三角形的重心,,四边形的面积为,那么的面积为 .
16.如图,矩形中,点,在轴上,交轴于点,点在上,,连接交轴于点,过点作轴交于点,点在函数的图象上.若的面积为,则的值为 .
17.如图,在中,D、E分别为边的中点,与交于点F,,如果,,那么=
18.在中,两条高所在直线交于点,若,则 .
19.在中,交于,交于,,,,那么 .
20.如图,在正方形ABCD中,DE=CE,AF=3DF,过点E作EG⊥BF于点H,交AD于点G.下列结论:
①△DEF∽△CBE;
②∠EBG=45°;
③AD=3AG.正确的有 .
三、解答题(本大题共5小题,每小题8分,共40分)
21.如图,铁道口的栏杆短臂长1米,长臂长16米,当短臂的端点下降0.5米时,求长臂端点应升高了多少米?
22.如图,在中,点,,分别在边,和上,连接,,得到四边形是菱形,若,,,求菱形的面积.
23.已知=k,求k2-3k-4的值.
24.(1)如图,在中,,,点、分别在射线、上(点不与点、点重合),且保持.
①若点在线段上,且,求线段的长;
②若,,求与之间的函数关系式,并写出的取值范围;
(2)正方形的边长为5(如图),点、分别在直线、上(点不与点、点重合),且保持.当时,写出线段的长(不需要计算过程,请直接写出结果).
25.如图1,已知二次函数的图象过点,,且与y轴交于点.
(1)求此二次函数的表达式;
(2)点E在此抛物线的对称轴上,且,求点E的坐标;
(3)如图2,点Q为x轴下方抛物线上一动点,直线AQ,BQ分别交y轴于点M,N,试探究的积是否存在最大值?若存在,请求出最大值及点Q的坐标;若不存在,请说明理由.
参考答案:
1.C
2.C
3.D
4.B
5.A
6.B
7.D
8.D
9.C
10.B
11.B
12.C
13.
14.17.5
15.27
16.
17.
18.或
19.1.5
20.①②③
21.8.
22.
23.-或6.
24.(1)①;②; (2) 或或或
25.(1)
(2)或
(3)存在,12,
