人教版数学九年级上册21.1一元二次方程教学设计
文档属性
| 名称 | 人教版数学九年级上册21.1一元二次方程教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 504.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-08 00:00:00 | ||
图片预览


文档简介
《21.1一元二次方程》教学设计
教学目标:
1.理解一元二次方程的概念;
2.掌握一元二次方程的一般式,正确认识二次项系数、一次项系数及常数项.
3. 通过生活学习数学,并用数学解决生活中的常见问题。
教学重点:一元二次方程的概念及其一般式。
教学难点:通过提出问题,建立一元二次方程的数学模型,再由一元一次方程的概念迁移到一元二次方程的概念。
教学过程
一、复习巩固
1.什么叫方程?我们学过哪些方程?
2.什么叫一元一次方程?
3.类比一元一次方程的定义,想一想:什么样的方程叫一元二次方程呢?
二、新课导入
活动1.情境导入
问题1:有一块矩形铁皮,长100cm,宽50cm,在它的四角各切去一个正方形,然后将四周凸出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600cm2,那么铁皮各角应切去多大的正方形?
解:设切去的正方形的边长为xcm,则盒底的长为(100-2x)cm,宽为(50-2x)cm,根据方盒的底面积为3600cm2,得
化简得
问题2:要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛
解:设比赛组织者应邀请x个队参加比赛.根据题意,列方程:
化简得
活动2.新知探究
方程①、②都不是一元一次方程.那么这两个方程与一元一次方程的区别在哪里?它们有什么共同特点呢?
①都是整式方程;②只含一个未知数;③未知数的最高次数是2.
一元二次方程的概念:像这样的等号两边都是整式, 只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程叫做一元二次方程.
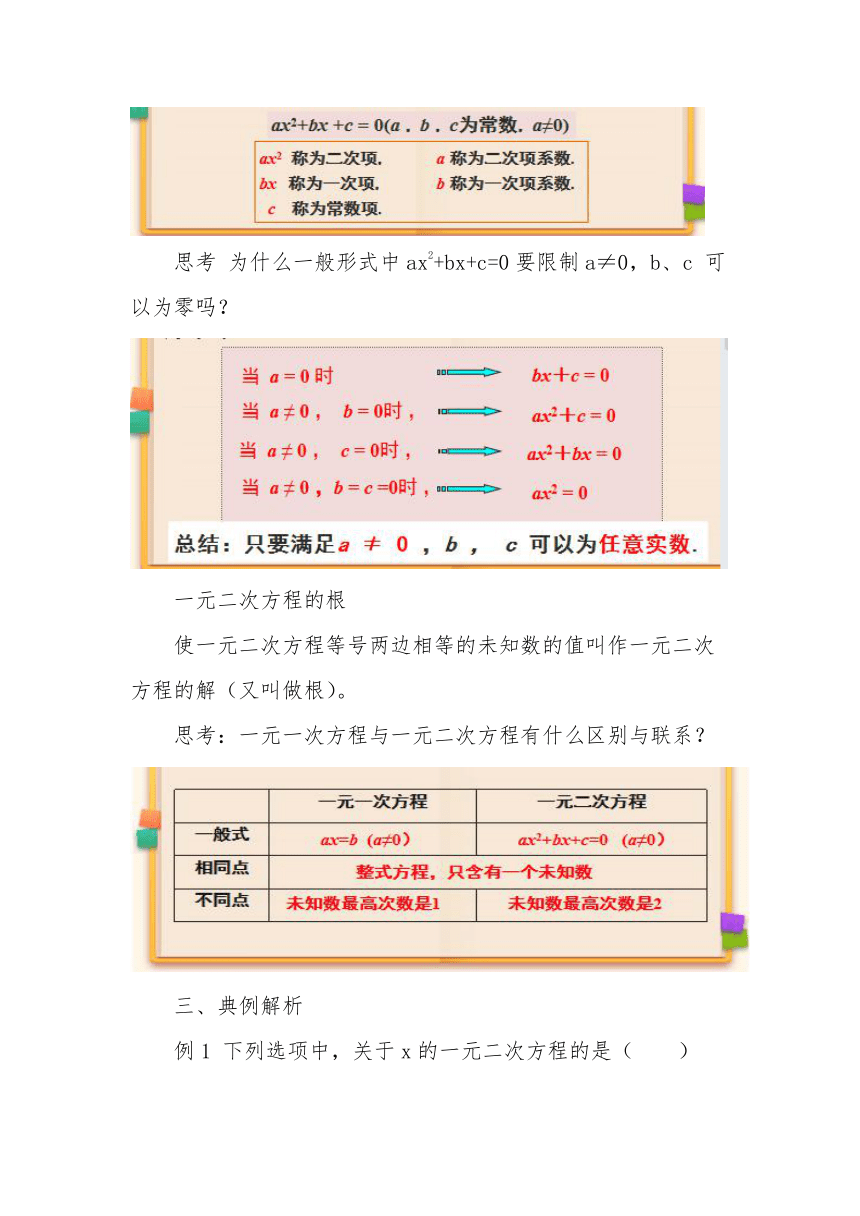
一元二次方程的一般形式
思考 为什么一般形式中ax2+bx+c=0要限制a≠0,b、c 可以为零吗?
一元二次方程的根
使一元二次方程等号两边相等的未知数的值叫作一元二次方程的解(又叫做根)。
思考:一元一次方程与一元二次方程有什么区别与联系?
三、典例解析
例1 下列选项中,关于x的一元二次方程的是( )
点睛:判断一个方程是不是一元二次方程,首先看是不是整式方程;如是再进一步化简整理后再作判断。
例2 a为何值时,下列方程为一元二次方程?
ax2-x=2x2 (2) (a-1)x |a|+1 -2x-7=0
点睛:用一元二次方程的定义求字母的值的方法:根据未知数的最高次数等于2,列出关于某个字母的方程,再排除使二次项系数等于0的字母的值。
例3 将方程3x(x-1)=5(x+2)化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数。
点睛:判定一元二次方程的二次项、一次项和常数项及它们的系数需要先将方程化为一般形式,再去判断;注意系数和项均包含前面的符号。
例4 已知a是方程 x2+2x-2=0 的一个实数根,求 2a2+4a+2018的值.
解:由题意得a2+2a-2=0即a2+2a=2
2a2+4a+2018=2(a2+2a)+2018=2022
四、课堂检测
1. 下列哪些是一元二次方程?
(1)3x+2=5x-2 (2)x2=0 (3)(x+3)(2x-4)=x2
(4)3y2=(3y+1)(y-2) (5)x2=x3+x2-1 (6)3x2=5x-1
2.填空
方程 一般形式 二次项 系数 一次项 系数 常数项
3.关于x的方程(k2-1)x2 + 2 (k-1) x + 2k + 2=0,
当k 时,是一元二次方程。
当k 时,是一元一次方程。
4.已知方程5x +mx-6=0的一个根为4,则m的值为_______.
5.(1) 如图,已知一矩形的长为200cm,宽150cm.现在矩形中挖去一个圆,使剩余部分的面积为原矩形面积的四分之三.求挖去的圆的半径xcm应满足的方程(其中π取3).
(2) 如图,据某市交通部门统计,前年该市汽车拥有量为75万辆,两年后增加到108万辆.求该市两年来汽车拥有量的年平均增长率x应满足的方程。
6.若关于x的一元二次方程(m+2)x2+5x+m2-4=0,有一个根为0,求m的值.
五、知识小结
一元二次方程的概念
一元二次方程的一般形式
一元二次方程的根
六、板书设计
教学反思:
一元二次方程在初中代数学习中,具有重要的地位,起着承前启后的作用。一方面对以前学习过的各种知识进行综合地应用另一方面,一元二次方程又是前面所学知识的继续和发展,它还是以后学习其他方程以及数学知识的基础。本节首先通过两个实际问题 --面积问题和比赛问题,进一步引出一元二次方程的具体例子,然后再引导学生观察并发现它们在形式上的共同点,得出一元二次方程的定义。概念课在教学中应结合学生实际情况出发,把握课堂的中心与各环节的时间分配,切忌增加过多内容而导致冲淡主题。
教学目标:
1.理解一元二次方程的概念;
2.掌握一元二次方程的一般式,正确认识二次项系数、一次项系数及常数项.
3. 通过生活学习数学,并用数学解决生活中的常见问题。
教学重点:一元二次方程的概念及其一般式。
教学难点:通过提出问题,建立一元二次方程的数学模型,再由一元一次方程的概念迁移到一元二次方程的概念。
教学过程
一、复习巩固
1.什么叫方程?我们学过哪些方程?
2.什么叫一元一次方程?
3.类比一元一次方程的定义,想一想:什么样的方程叫一元二次方程呢?
二、新课导入
活动1.情境导入
问题1:有一块矩形铁皮,长100cm,宽50cm,在它的四角各切去一个正方形,然后将四周凸出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600cm2,那么铁皮各角应切去多大的正方形?
解:设切去的正方形的边长为xcm,则盒底的长为(100-2x)cm,宽为(50-2x)cm,根据方盒的底面积为3600cm2,得
化简得
问题2:要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛
解:设比赛组织者应邀请x个队参加比赛.根据题意,列方程:
化简得
活动2.新知探究
方程①、②都不是一元一次方程.那么这两个方程与一元一次方程的区别在哪里?它们有什么共同特点呢?
①都是整式方程;②只含一个未知数;③未知数的最高次数是2.
一元二次方程的概念:像这样的等号两边都是整式, 只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程叫做一元二次方程.
一元二次方程的一般形式
思考 为什么一般形式中ax2+bx+c=0要限制a≠0,b、c 可以为零吗?
一元二次方程的根
使一元二次方程等号两边相等的未知数的值叫作一元二次方程的解(又叫做根)。
思考:一元一次方程与一元二次方程有什么区别与联系?
三、典例解析
例1 下列选项中,关于x的一元二次方程的是( )
点睛:判断一个方程是不是一元二次方程,首先看是不是整式方程;如是再进一步化简整理后再作判断。
例2 a为何值时,下列方程为一元二次方程?
ax2-x=2x2 (2) (a-1)x |a|+1 -2x-7=0
点睛:用一元二次方程的定义求字母的值的方法:根据未知数的最高次数等于2,列出关于某个字母的方程,再排除使二次项系数等于0的字母的值。
例3 将方程3x(x-1)=5(x+2)化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数。
点睛:判定一元二次方程的二次项、一次项和常数项及它们的系数需要先将方程化为一般形式,再去判断;注意系数和项均包含前面的符号。
例4 已知a是方程 x2+2x-2=0 的一个实数根,求 2a2+4a+2018的值.
解:由题意得a2+2a-2=0即a2+2a=2
2a2+4a+2018=2(a2+2a)+2018=2022
四、课堂检测
1. 下列哪些是一元二次方程?
(1)3x+2=5x-2 (2)x2=0 (3)(x+3)(2x-4)=x2
(4)3y2=(3y+1)(y-2) (5)x2=x3+x2-1 (6)3x2=5x-1
2.填空
方程 一般形式 二次项 系数 一次项 系数 常数项
3.关于x的方程(k2-1)x2 + 2 (k-1) x + 2k + 2=0,
当k 时,是一元二次方程。
当k 时,是一元一次方程。
4.已知方程5x +mx-6=0的一个根为4,则m的值为_______.
5.(1) 如图,已知一矩形的长为200cm,宽150cm.现在矩形中挖去一个圆,使剩余部分的面积为原矩形面积的四分之三.求挖去的圆的半径xcm应满足的方程(其中π取3).
(2) 如图,据某市交通部门统计,前年该市汽车拥有量为75万辆,两年后增加到108万辆.求该市两年来汽车拥有量的年平均增长率x应满足的方程。
6.若关于x的一元二次方程(m+2)x2+5x+m2-4=0,有一个根为0,求m的值.
五、知识小结
一元二次方程的概念
一元二次方程的一般形式
一元二次方程的根
六、板书设计
教学反思:
一元二次方程在初中代数学习中,具有重要的地位,起着承前启后的作用。一方面对以前学习过的各种知识进行综合地应用另一方面,一元二次方程又是前面所学知识的继续和发展,它还是以后学习其他方程以及数学知识的基础。本节首先通过两个实际问题 --面积问题和比赛问题,进一步引出一元二次方程的具体例子,然后再引导学生观察并发现它们在形式上的共同点,得出一元二次方程的定义。概念课在教学中应结合学生实际情况出发,把握课堂的中心与各环节的时间分配,切忌增加过多内容而导致冲淡主题。
同课章节目录
