正多边形和圆课件

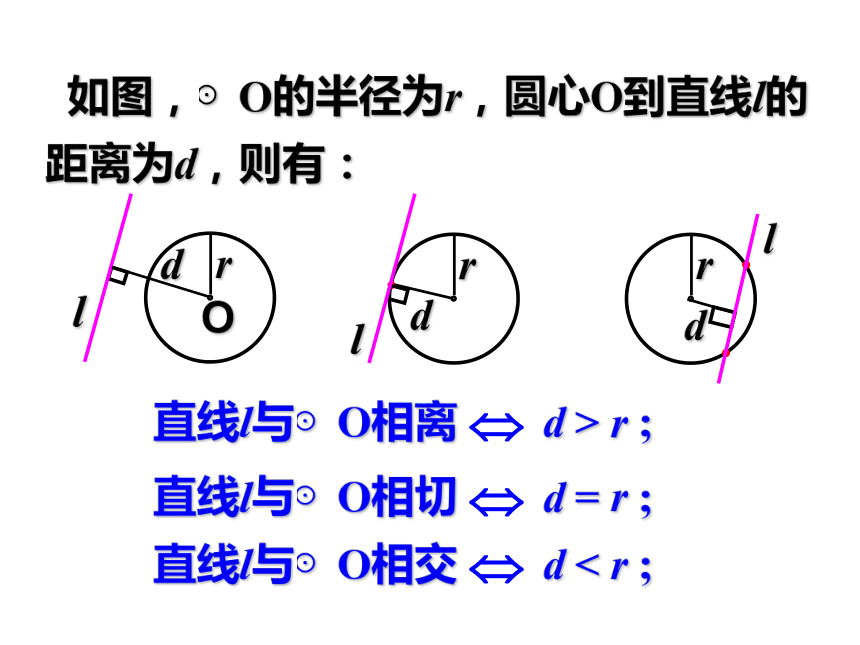
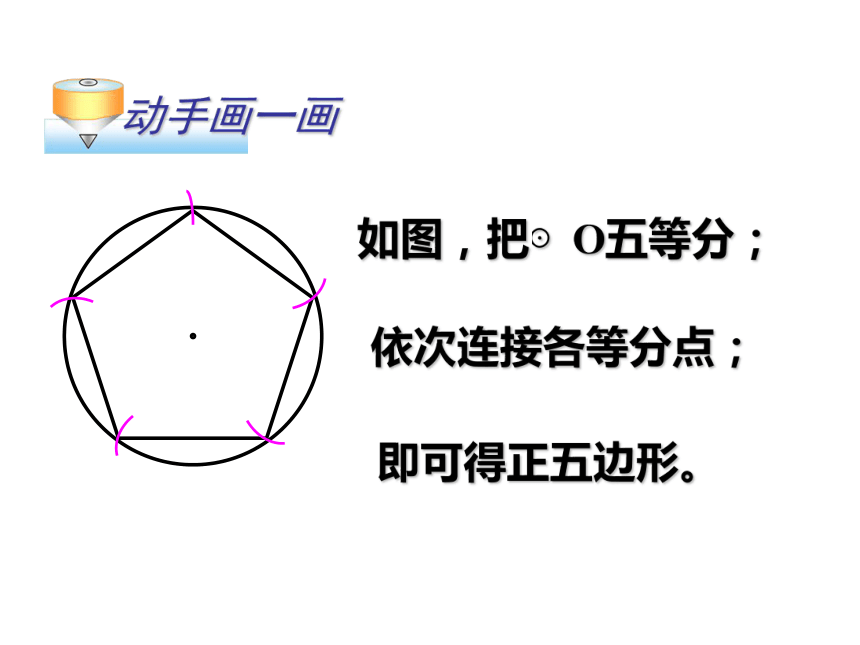
课件25张PPT。正多边形与圆 设⊙O的半径为r，点P到圆心的距离OP=d，则有：点P在圆外 d > r ;点P在圆上 d = r ;点P在圆内 d < r ; 不在同一直线上的三点确定一个圆。复 习 回 顾rrrdOldldl 如图，⊙O的半径为r，圆心O到直线l的距离为d，则有：直线l与⊙O相离 d > r ;直线l与⊙O相切 d = r ;直线l与⊙O相交 d < r ; 我们知道，各边相等，各角也相等的多边形是正多边形。日常生活中,我们经常能看到正多边形形状的物体,利用正多边形，我们也可以得到许多美丽的图案，你能举出一些这样的例子吗？ 怎样可以快捷地画出一个正五边形？把圆五等分即可。如图，把⊙O五等分；依次连接各等分点；即可得正五边形。动手画一画 如何画一个边长为2cm的正六边形？ 我们知道，把圆六等分，再依次连接各等分点即可得到一个正六边形。但半径为多少的圆，六等分后得到的正六边形的边长为2cm？故我们需要知道圆的半径与正多边形边长之间的关系。 把一个圆等分得到的正多边形叫做这个圆的内接多边形，这个圆就叫做正多边形的外接圆。 如图，五边形ABCDE是⊙O的内接正五边形，⊙O是五边形ABCDE的外接圆。识 记 我们把一个正多边形的 外接圆的圆心叫做这个正多 边形的中心，外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角，中心到正多边形的一边的距离叫做正多边形的边心距.识 记中心角半径边心距 1、正五边形的边和半径形成了怎样的三角形？
2、这些三角形间有怎样的关系？结论： 正五边形5条半径分正五边形为5个全等的等腰三角形。探究1 正六边形6条半径分正六边形为6个全等的等腰三角形。正六边形 正四边形、正五边形、正六边形的边心距有什么特征呢？ 探 究 2正n边形的n条边心距相等. 正n边形的n条边心距又把n个全等的三角形分成了怎样的图形？它们之间又有什么样的关系？ 结论： 正n边 形 的n 条 边心 距 又把 n 个 全等 的三角形 分成了2n个全等 的直角三角形。探 究 3 一个亭子的地基是半径为4m的正六边形，求地基的周长和面积(精确到0.1m2).例 题 先根据题意，画出正六边形，已知正六边形的半径为4m，要求正六边形的周长和面积，需要先求出正六边形的边长。半径和边长同在一个三角形中，所以利用半径求边长则要构建三角形求解.M解：正六边形的中心角为连接OB，OC，过点O作OM⊥BC于点M.∵OB=OC, ∠BOC=60°∴△OBC为等边三角形.∴BC=OB=4m∴C正六边形ABCDEF=4×6=24mM在△OBC中，在Rt△OBC中， 现在你知道怎么画一个边长为2cm的正六边形了吗？如图，连接OB、OC，易证△OBC为等边三角形，故圆的半径等于正六边形的边长。探 究3、已知圆外接正方形的边长为2cm，则该圆外切正三角形的半径是 .
4、正三角形的边长等于a,则它的高h,边心距r,半径R的比h:r:R= .巩 固 练 习 1、正三角形边长为a，它的外接圆半径等于 ，边心距等于 . 2、已知圆内接正三角形的边心距等于 ，则这圆外切正六边形的边心距等于 .2cm3：1：2； 用48m长的篱笆在空地上围成一个绿化场地，现有几种设计方案，正三角形、正方形、正六边形、圆，哪种场地的面积最大？
谢谢！