湖南省益阳市箴言中学2015届高三理科数学高考指导讲座(2015年4月)
文档属性
| 名称 | 湖南省益阳市箴言中学2015届高三理科数学高考指导讲座(2015年4月) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-30 19:35:21 | ||
图片预览


文档简介
(共31张PPT)
2015年理科数学高考指导
高三数学备课组
2015.04.28
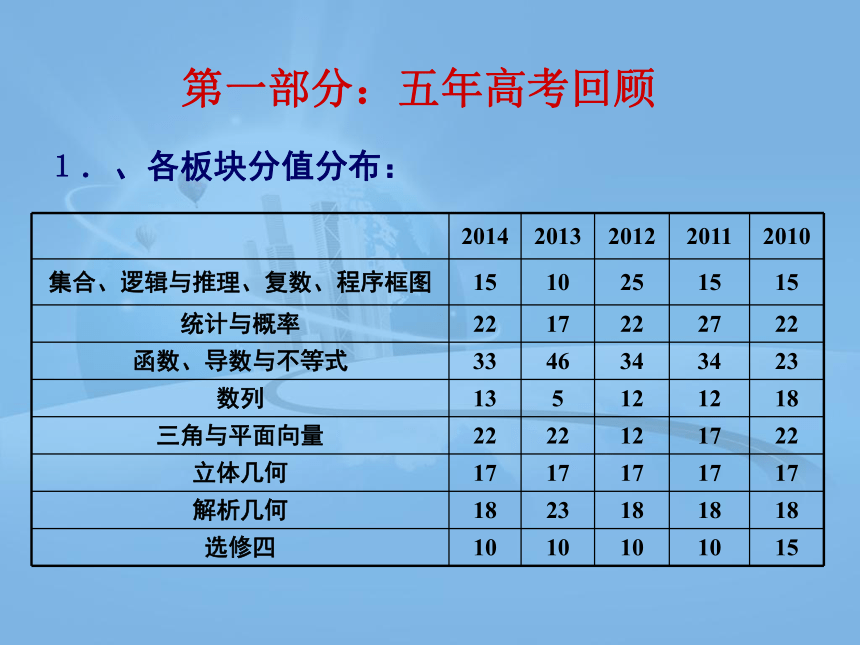
第一部分:五年高考回顾
、各板块分值分布:
2014 2013 2012 2011 2010
集合、逻辑与推理、复数、程序框图 15 10 25 15 15
统计与概率 22 17 22 27 22
函数、导数与不等式 33 46 34 34 23
数列 13 5 12 12 18
三角与平面向量 22 22 12 17 22
立体几何 17 17 17 17 17
解析几何 18 23 18 18 18
选修四 10 10 10 10 15
二、各板块考试内容一览
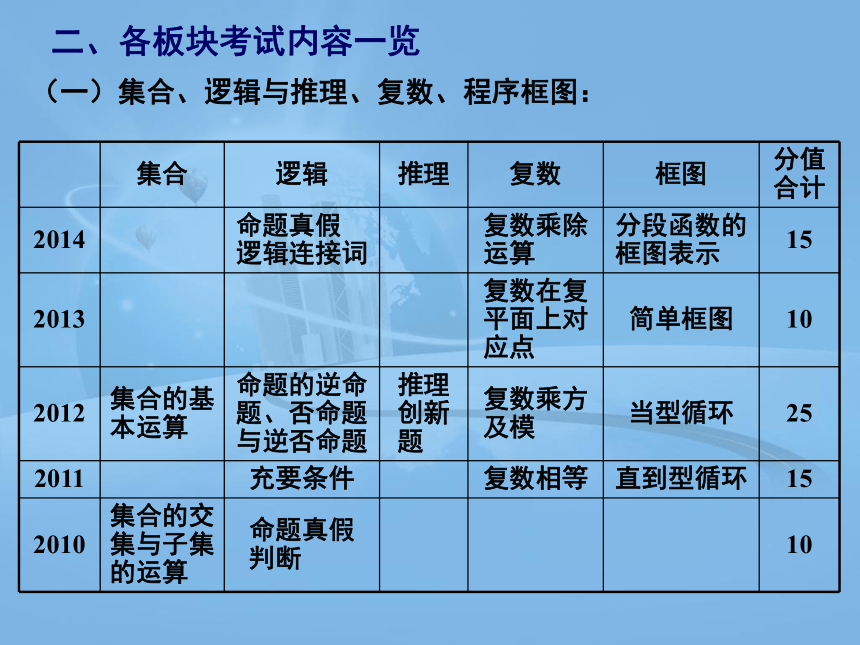
(一)集合、逻辑与推理、复数、程序框图:
集合 逻辑 推理 复数 框图 分值合计
2014 命题真假 逻辑连接词 复数乘除运算 分段函数的框图表示 15
2013 复数在复平面上对应点 简单框图 10
2012 集合的基本运算 命题的逆命题、否命题与逆否命题 推理创新题 复数乘方及模 当型循环 25
2011 充要条件 复数相等 直到型循环 15
2010 集合的交集与子集的运算 命题真假 判断 10
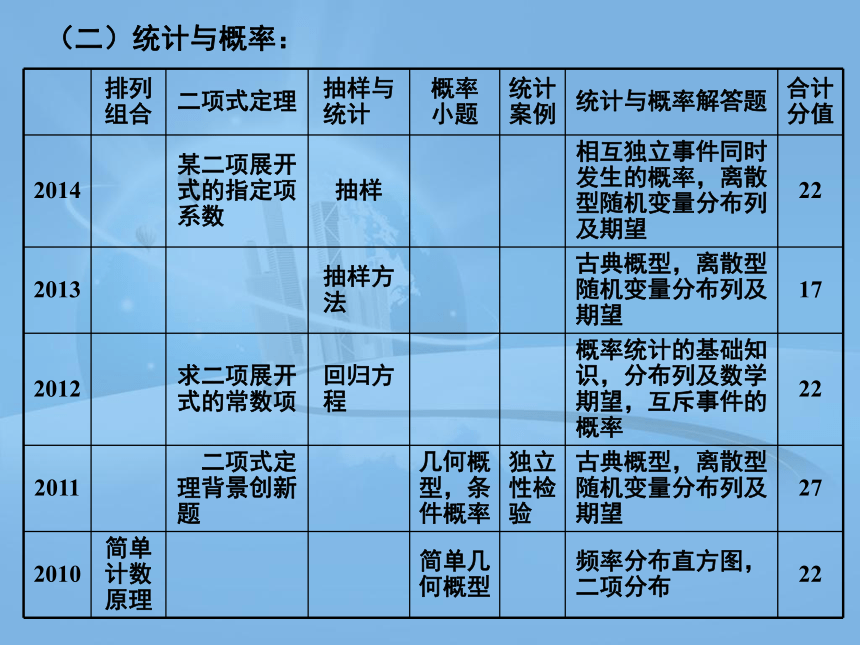
(二)统计与概率:
排列组合 二项式定理 抽样与统计 概率 小题 统计案例 统计与概率解答题 合计分值
2014 某二项展开式的指定项系数 抽样 相互独立事件同时发生的概率,离散型随机变量分布列及期望 22
2013 抽样方法 古典概型,离散型随机变量分布列及期望 17
2012 求二项展开式的常数项 回归方程 概率统计的基础知识,分布列及数学期望,互斥事件的概率 22
2011 二项式定理背景创新题 几何概型,条件概率 独立性检验 古典概型,离散型随机变量分布列及期望 27
2010 简单计数原理 简单几何概型 频率分布直方图,二项分布 22
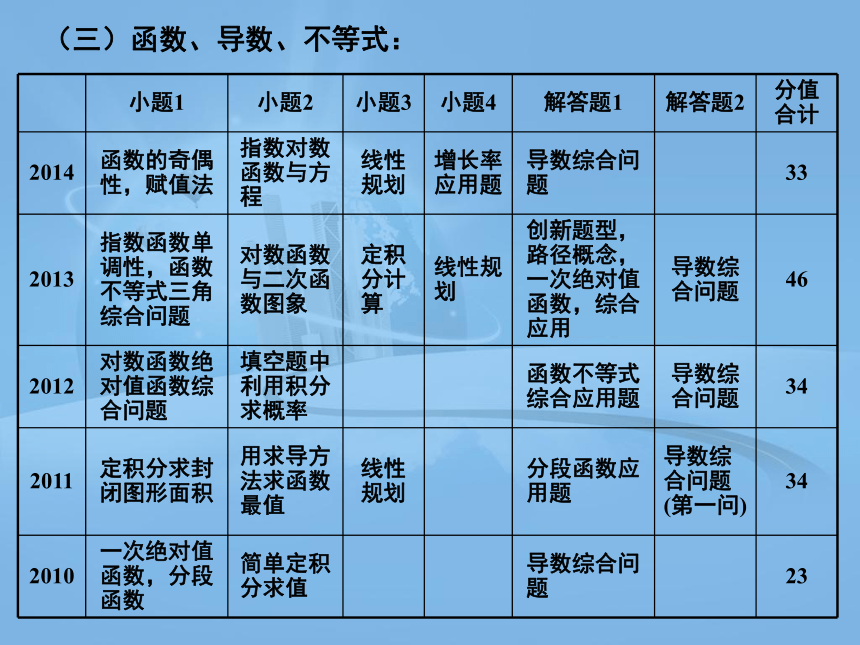
(三)函数、导数、不等式:
小题1 小题2 小题3 小题4 解答题1 解答题2 分值合计
2014 函数的奇偶性,赋值法 指数对数函数与方程 线性规划 增长率应用题 导数综合问题 33
2013 指数函数单调性,函数不等式三角综合问题 对数函数与二次函数图象 定积分计算 线性规划 创新题型,路径概念,一次绝对值函数,综合应用 导数综合问题 46
2012 对数函数绝对值函数综合问题 填空题中利用积分求概率 函数不等式综合应用题 导数综合问题 34
2011 定积分求封闭图形面积 用求导方法求函数最值 线性规划 分段函数应用题 导数综合问题(第一问) 34
2010 一次绝对值函数,分段函数 简单定积分求值 导数综合问题 23
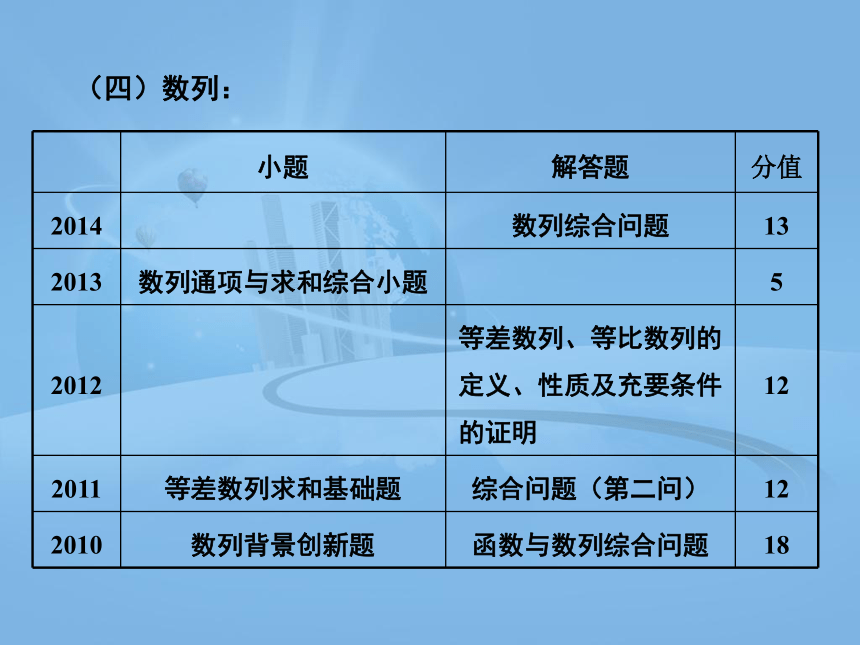
(四)数列:
小题 解答题 分值
2014 数列综合问题 13
2013 数列通项与求和综合小题 5
2012 等差数列、等比数列的 定义、性质及充要条件 的证明 12
2011 等差数列求和基础题 综合问题(第二问) 12
2010 数列背景创新题 函数与数列综合问题 18
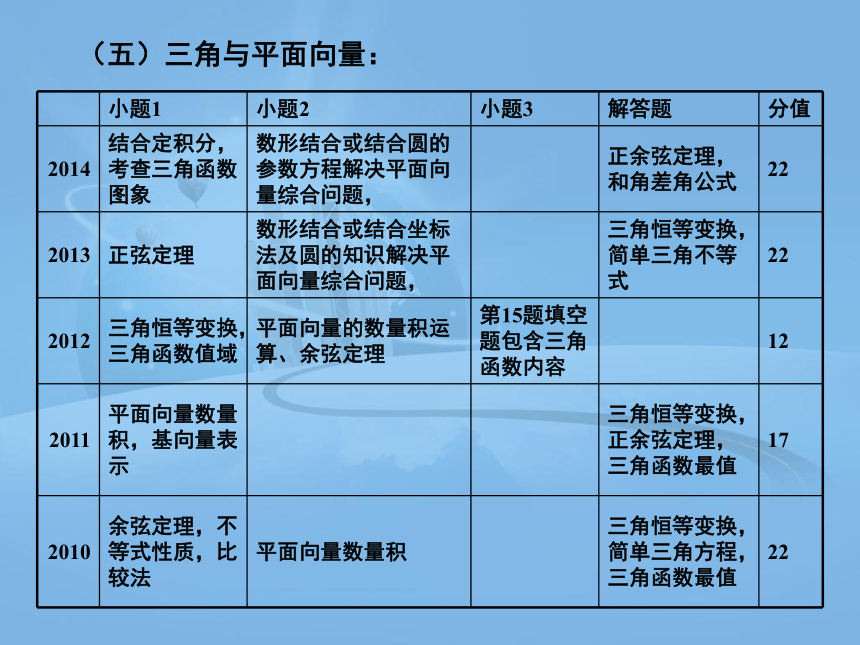
(五)三角与平面向量:
小题1 小题2 小题3 解答题 分值
2014 结合定积分,考查三角函数图象 数形结合或结合圆的参数方程解决平面向量综合问题, 正余弦定理,和角差角公式 22
2013 正弦定理 数形结合或结合坐标法及圆的知识解决平面向量综合问题, 三角恒等变换,简单三角不等式 22
2012 三角恒等变换,三角函数值域 平面向量的数量积运算、余弦定理 第15题填空题包含三角函数内容 12
2011 平面向量数量积,基向量表示 三角恒等变换,正余弦定理,三角函数最值 17
2010 余弦定理,不等式性质,比较法 平面向量数量积 三角恒等变换,简单三角方程,三角函数最值 22
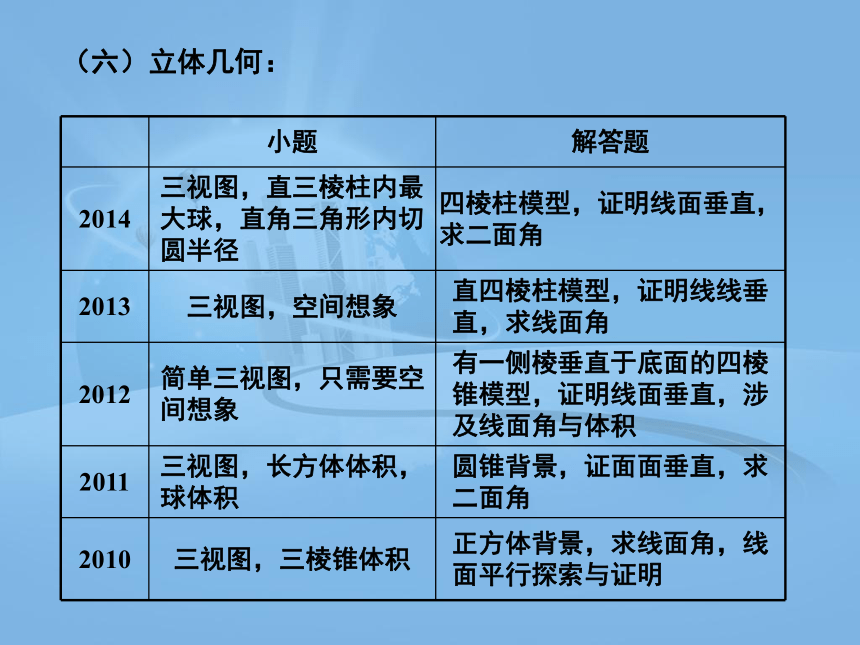
(六)立体几何:
小题 解答题
2014 三视图,直三棱柱内最大球,直角三角形内切圆半径 四棱柱模型,证明线面垂直,求二面角
2013 三视图,空间想象 直四棱柱模型,证明线线垂直,求线面角
2012 简单三视图,只需要空间想象 有一侧棱垂直于底面的四棱锥模型,证明线面垂直,涉及线面角与体积
2011 三视图,长方体体积,球体积 圆锥背景,证面面垂直,求二面角
2010 三视图,三棱锥体积 正方体背景,求线面角,线面平行探索与证明
(七)解析几何:
小题 解答题
2014 抛物线。点的坐标代入抛物线方程。 椭圆,双曲线,四边形面积最小值。
2013 小题1:双曲线。利用双曲线定义及余弦定理,求离心率。 直线与抛物线方程联立,韦达定理,向量数量积;圆的方程,相交两个圆公共弦所在直线方程,点到直线距离;
小题2:对称问题,化反射为直射问题。
2012 比较基础的双曲线问题。 直接法或定义法求抛物线方程;直线与圆的位置关系,直线与抛物线方程联立,多次利用韦达定理,定值问题。
2011 双曲线渐近线问题。 椭圆、抛物线。直线与椭圆、直线与抛物线联立,三角形面积问题。
2010 抛物线。直线与抛物线方程联立,梯形面积转化为,再利用韦达定理求参数。 应用题。冰川融化问题。第一问是简单的利用定义求曲线方程;直线与椭圆、直线与圆的位置关系,等比数列求和公式,综合数学建模。
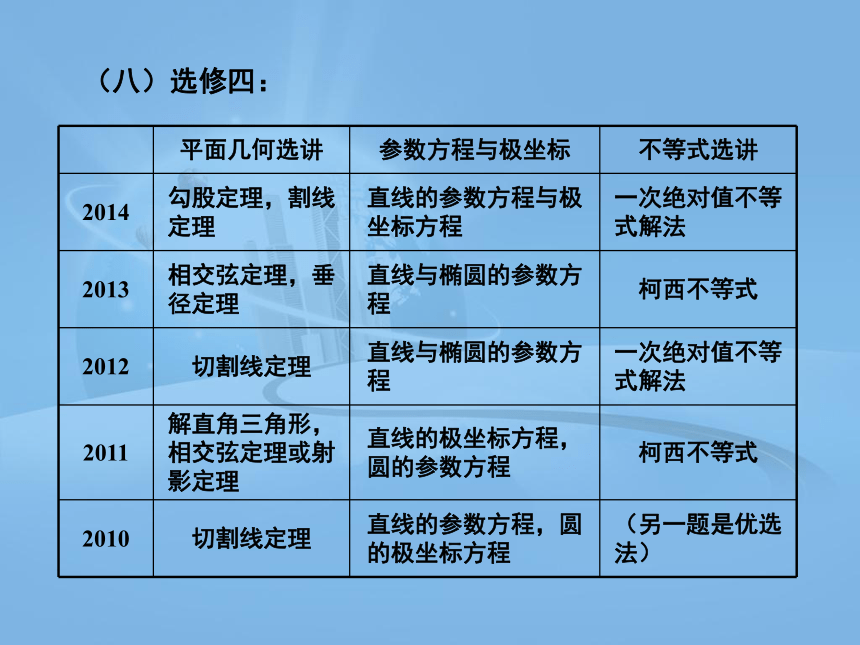
(八)选修四:
平面几何选讲 参数方程与极坐标 不等式选讲
2014 勾股定理,割线定理 直线的参数方程与极坐标方程 一次绝对值不等式解法
2013 相交弦定理,垂径定理 直线与椭圆的参数方程 柯西不等式
2012 切割线定理 直线与椭圆的参数方程 一次绝对值不等式解法
2011 解直角三角形,相交弦定理或射影定理 直线的极坐标方程,圆的参数方程 柯西不等式
2010 切割线定理 直线的参数方程,圆的极坐标方程 (另一题是优选法)
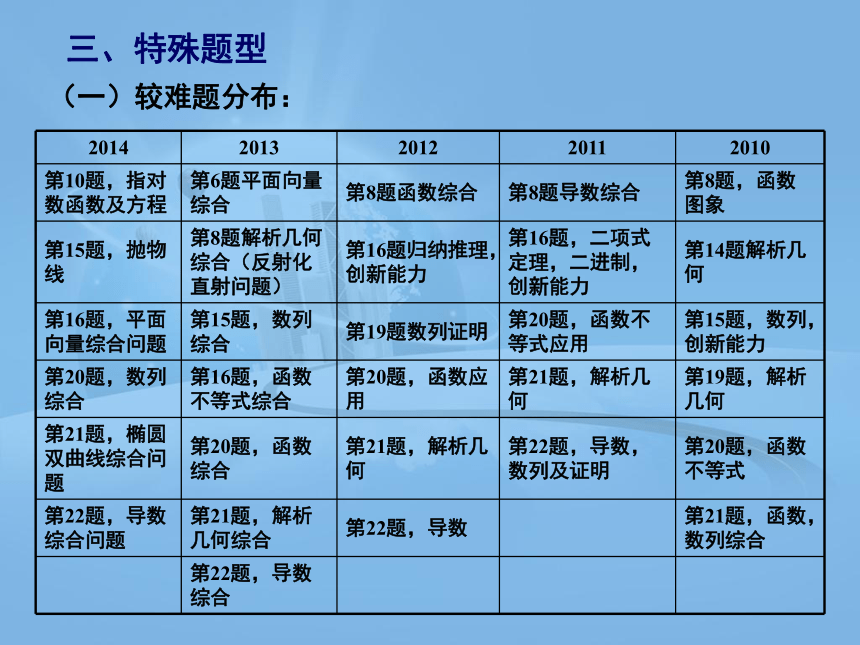
三、特殊题型
(一)较难题分布:
2014 2013 2012 2011 2010
第10题,指对数函数及方程 第6题平面向量综合 第8题函数综合 第8题导数综合 第8题,函数图象
第15题,抛物线 第8题解析几何综合(反射化直射问题) 第16题归纳推理,创新能力 第16题,二项式定理,二进制,创新能力 第14题解析几何
第16题,平面向量综合问题 第15题,数列综合 第19题数列证明 第20题,函数不等式应用 第15题,数列,创新能力
第20题,数列综合 第16题,函数不等式综合 第20题,函数应用 第21题,解析几何 第19题,解析几何
第21题,椭圆双曲线综合问题 第20题,函数综合 第21题,解析几何 第22题,导数,数列及证明 第20题,函数不等式
第22题,导数综合问题 第21题,解析几何综合 第22题,导数 第21题,函数,数列综合
第22题,导数综合
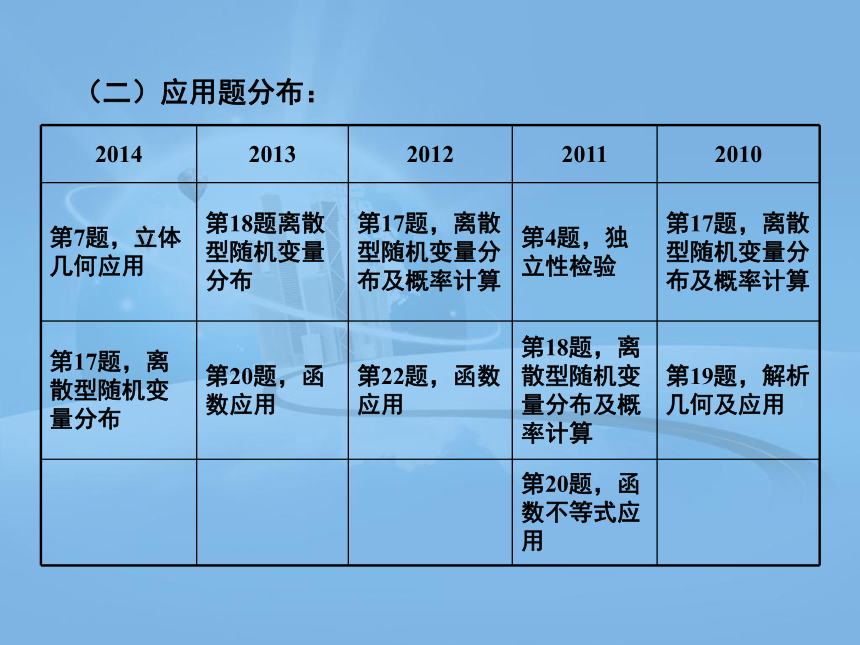
(二)应用题分布:
2014 2013 2012 2011 2010
第7题,立体几何应用 第18题离散型随机变量分布 第17题,离散型随机变量分布及概率计算 第4题,独立性检验 第17题,离散型随机变量分布及概率计算
第17题,离散型随机变量分布 第20题,函数应用 第22题,函数应用 第18题,离散型随机变量分布及概率计算 第19题,解析几何及应用
第20题,函数不等式应用
总的感受
湖南高考理科数学的难度比较稳定,并且注意梯度,哪些内容该难,哪些内容该容易,比较明确;
第二部分:考试说明解读
如何阅读考试说明?
考纲要求是总筋,
考纲阐释是明示,
题型示例是暗示
特别关注:
特别关注:
希 望
1、有分析,但不局限于分析;
2、有预测,但最后阶段才用预测;
3、通过分析和预测,提高我们的研究能力和教学能力。
4、祝贺大家的学生,高考中都取得好成绩!
2015年理科数学高考指导
高三数学备课组
2015.04.28
第一部分:五年高考回顾
、各板块分值分布:
2014 2013 2012 2011 2010
集合、逻辑与推理、复数、程序框图 15 10 25 15 15
统计与概率 22 17 22 27 22
函数、导数与不等式 33 46 34 34 23
数列 13 5 12 12 18
三角与平面向量 22 22 12 17 22
立体几何 17 17 17 17 17
解析几何 18 23 18 18 18
选修四 10 10 10 10 15
二、各板块考试内容一览
(一)集合、逻辑与推理、复数、程序框图:
集合 逻辑 推理 复数 框图 分值合计
2014 命题真假 逻辑连接词 复数乘除运算 分段函数的框图表示 15
2013 复数在复平面上对应点 简单框图 10
2012 集合的基本运算 命题的逆命题、否命题与逆否命题 推理创新题 复数乘方及模 当型循环 25
2011 充要条件 复数相等 直到型循环 15
2010 集合的交集与子集的运算 命题真假 判断 10
(二)统计与概率:
排列组合 二项式定理 抽样与统计 概率 小题 统计案例 统计与概率解答题 合计分值
2014 某二项展开式的指定项系数 抽样 相互独立事件同时发生的概率,离散型随机变量分布列及期望 22
2013 抽样方法 古典概型,离散型随机变量分布列及期望 17
2012 求二项展开式的常数项 回归方程 概率统计的基础知识,分布列及数学期望,互斥事件的概率 22
2011 二项式定理背景创新题 几何概型,条件概率 独立性检验 古典概型,离散型随机变量分布列及期望 27
2010 简单计数原理 简单几何概型 频率分布直方图,二项分布 22
(三)函数、导数、不等式:
小题1 小题2 小题3 小题4 解答题1 解答题2 分值合计
2014 函数的奇偶性,赋值法 指数对数函数与方程 线性规划 增长率应用题 导数综合问题 33
2013 指数函数单调性,函数不等式三角综合问题 对数函数与二次函数图象 定积分计算 线性规划 创新题型,路径概念,一次绝对值函数,综合应用 导数综合问题 46
2012 对数函数绝对值函数综合问题 填空题中利用积分求概率 函数不等式综合应用题 导数综合问题 34
2011 定积分求封闭图形面积 用求导方法求函数最值 线性规划 分段函数应用题 导数综合问题(第一问) 34
2010 一次绝对值函数,分段函数 简单定积分求值 导数综合问题 23
(四)数列:
小题 解答题 分值
2014 数列综合问题 13
2013 数列通项与求和综合小题 5
2012 等差数列、等比数列的 定义、性质及充要条件 的证明 12
2011 等差数列求和基础题 综合问题(第二问) 12
2010 数列背景创新题 函数与数列综合问题 18
(五)三角与平面向量:
小题1 小题2 小题3 解答题 分值
2014 结合定积分,考查三角函数图象 数形结合或结合圆的参数方程解决平面向量综合问题, 正余弦定理,和角差角公式 22
2013 正弦定理 数形结合或结合坐标法及圆的知识解决平面向量综合问题, 三角恒等变换,简单三角不等式 22
2012 三角恒等变换,三角函数值域 平面向量的数量积运算、余弦定理 第15题填空题包含三角函数内容 12
2011 平面向量数量积,基向量表示 三角恒等变换,正余弦定理,三角函数最值 17
2010 余弦定理,不等式性质,比较法 平面向量数量积 三角恒等变换,简单三角方程,三角函数最值 22
(六)立体几何:
小题 解答题
2014 三视图,直三棱柱内最大球,直角三角形内切圆半径 四棱柱模型,证明线面垂直,求二面角
2013 三视图,空间想象 直四棱柱模型,证明线线垂直,求线面角
2012 简单三视图,只需要空间想象 有一侧棱垂直于底面的四棱锥模型,证明线面垂直,涉及线面角与体积
2011 三视图,长方体体积,球体积 圆锥背景,证面面垂直,求二面角
2010 三视图,三棱锥体积 正方体背景,求线面角,线面平行探索与证明
(七)解析几何:
小题 解答题
2014 抛物线。点的坐标代入抛物线方程。 椭圆,双曲线,四边形面积最小值。
2013 小题1:双曲线。利用双曲线定义及余弦定理,求离心率。 直线与抛物线方程联立,韦达定理,向量数量积;圆的方程,相交两个圆公共弦所在直线方程,点到直线距离;
小题2:对称问题,化反射为直射问题。
2012 比较基础的双曲线问题。 直接法或定义法求抛物线方程;直线与圆的位置关系,直线与抛物线方程联立,多次利用韦达定理,定值问题。
2011 双曲线渐近线问题。 椭圆、抛物线。直线与椭圆、直线与抛物线联立,三角形面积问题。
2010 抛物线。直线与抛物线方程联立,梯形面积转化为,再利用韦达定理求参数。 应用题。冰川融化问题。第一问是简单的利用定义求曲线方程;直线与椭圆、直线与圆的位置关系,等比数列求和公式,综合数学建模。
(八)选修四:
平面几何选讲 参数方程与极坐标 不等式选讲
2014 勾股定理,割线定理 直线的参数方程与极坐标方程 一次绝对值不等式解法
2013 相交弦定理,垂径定理 直线与椭圆的参数方程 柯西不等式
2012 切割线定理 直线与椭圆的参数方程 一次绝对值不等式解法
2011 解直角三角形,相交弦定理或射影定理 直线的极坐标方程,圆的参数方程 柯西不等式
2010 切割线定理 直线的参数方程,圆的极坐标方程 (另一题是优选法)
三、特殊题型
(一)较难题分布:
2014 2013 2012 2011 2010
第10题,指对数函数及方程 第6题平面向量综合 第8题函数综合 第8题导数综合 第8题,函数图象
第15题,抛物线 第8题解析几何综合(反射化直射问题) 第16题归纳推理,创新能力 第16题,二项式定理,二进制,创新能力 第14题解析几何
第16题,平面向量综合问题 第15题,数列综合 第19题数列证明 第20题,函数不等式应用 第15题,数列,创新能力
第20题,数列综合 第16题,函数不等式综合 第20题,函数应用 第21题,解析几何 第19题,解析几何
第21题,椭圆双曲线综合问题 第20题,函数综合 第21题,解析几何 第22题,导数,数列及证明 第20题,函数不等式
第22题,导数综合问题 第21题,解析几何综合 第22题,导数 第21题,函数,数列综合
第22题,导数综合
(二)应用题分布:
2014 2013 2012 2011 2010
第7题,立体几何应用 第18题离散型随机变量分布 第17题,离散型随机变量分布及概率计算 第4题,独立性检验 第17题,离散型随机变量分布及概率计算
第17题,离散型随机变量分布 第20题,函数应用 第22题,函数应用 第18题,离散型随机变量分布及概率计算 第19题,解析几何及应用
第20题,函数不等式应用
总的感受
湖南高考理科数学的难度比较稳定,并且注意梯度,哪些内容该难,哪些内容该容易,比较明确;
第二部分:考试说明解读
如何阅读考试说明?
考纲要求是总筋,
考纲阐释是明示,
题型示例是暗示
特别关注:
特别关注:
希 望
1、有分析,但不局限于分析;
2、有预测,但最后阶段才用预测;
3、通过分析和预测,提高我们的研究能力和教学能力。
4、祝贺大家的学生,高考中都取得好成绩!
同课章节目录
