人教版 九年级上册 实际问题与二次函数之几何图形的最大面积 课件(共18张PPT)
文档属性
| 名称 | 人教版 九年级上册 实际问题与二次函数之几何图形的最大面积 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 198.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-08 15:26:41 | ||
图片预览






文档简介
(共18张PPT)
实际问题与二次函数之
人教版数学九年级上册
几何图形的最大面积
1.分析实际问题中变量之间的二次函数关系;(难点)
2.会运用二次函数求实际问题中的最大值或最小值;
3.能应用二次函数的性质解决图形中最大面积问题。(重点)
4.通过用二次函数解决生活中的问题,体会函数知识的应用价值,感受数学与人类生活的密切联系。
一、教学目标
求二次函数y=ax2+bx+c(a≠0)最值?
将y=ax2+bx+c(a≠0)化为y=a(x-h)2+k的形式,当x=h时,函数y取得最大(小)值,为k。
当x= 时,函数y取得最大(小)值,为 。
二、复习引入
配方法
公式法
例:用总长为60米的篱笆围成矩形场地,矩形面积S(平方米)随矩形一边长l(米)的变化而变化。当l是多少米时,场地的面积S最大?
典例精析
问题1 面积S的函数关系式是什么?
S=(30-l)l=-l2+30l
三、探究二次函数解决矩形面积问题
问题2 当l是多少米时,场地的面积S最大?
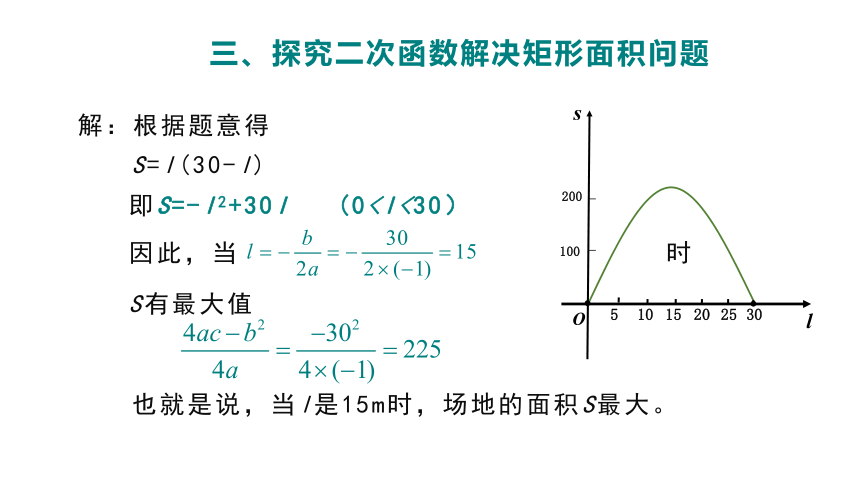
解:根据题意得
S=l(30-l)
即S=-l2+30l (0因此,当 时
S有最大值
也就是说,当l是15m时,场地的面积S最大。
三、探究二次函数解决矩形面积问题
5
10
15
20
25
30
100
200
l
s
O
如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园。
60-2x
x
x
(1)当墙长32m时,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
分析:设垂直于墙的边长为x m,则平行于墙的边长为________ m
矩形菜园的面积S =________________________
想一想:如何求解自变量x的取值范围?
0<60-2x≤32,即14≤x<30
(60-2x)
x(60-2x)=-2x2+60x
变式
三、探究二次函数解决矩形面积问题
三、探究二次函数解决矩形面积问题
解:设垂直于墙的边长为x m,则平行于墙的边长为(60-2x)m
∴矩形菜园的面积S=x(60-2x)=-2x2+60x
由题意得0<60-2x≤32,即14≤x<30
∵S=-2x2+60x=-2(x2-30x)=-2(x-15)2+450
∴当x=15m时,S取最大值,此时S=450m2
设未知数,用含未知数的代数式表示相关量
根据题意,求出自变量的取值范围
写出二次函数解析式,化为顶点式
结合相关量,利用面积公式求解
结合自变量的取值范围可知,该二次函数在其顶点处取得最大值。
(2)当墙长18 m时,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
解:设垂直于墙的边长为x m
由(1)知S=-2x2+60x=-2(x2-30x)=-2(x-15)2+450
问题1 与(1)有什么区别?
试一试 在(2)中,求自变量的取值范围?
21≤ x <30
是否依然在x=15时,S取得最大值?
三、探究二次函数解决矩形面积问题
问题2 当21≤ x <30时,S的值随x的增大,是如何变化的? 当x取何值时,S取得最大值?
当21≤ x <30时,S 随x的增大而减小
当 x =21时,S取得最大值
此时S=-2×(21-15)2+450=378m2
三、探究二次函数解决矩形面积问题
实际问题中求解二次函数最值问题,不一定都取图象顶点处,要根据自变量在实际情况中的取值范围进行分析。
通过前两道例题的对比,理解函数图象的顶点、端点与最值的关系以及何时取顶点处、何时取端点处才有符合实际的最值。
三、探究二次函数解决矩形面积问题
“何时取得最大面积” 解题思路
1、设自变量(一般设某条边为x,)与因变量(设“面积”为y);
2、列出y与x的函数关系式(一般为二次函数);
3、找出自变量的取值范围;
4、求利用配方法或顶点公式,求出最值。若自变量的取值范围不包括顶点横坐标,则须利用增减性求出最值。
三、探究二次函数解决矩形面积问题
如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有
二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。
四、课堂练习
拓展练习
A
B
C
D
A
B
C
D
解:
(1)∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3)∵墙的可用长度为8米
(2)当x= 时,S最大值= =36(平方米)
∴ S=x(24-4x)=-4x2+24 x (0∴ 0<24-4x ≤8 4≤x<6
∴当x=4m时,S最大值=32 平方米
x
24-4x
四、课堂练习
拓展练习
(福建中考)如图,在足够大的空地上有一段长为 a m的旧墙 MN,某人利用旧墙和木栏围成一个矩形菜园 ABCD,其中 AD≤MN。已知矩形菜园的一边靠墙,另三边一共用了 100 m木栏。
四、课后作业
对接中考
(1)若 a=20,所围成的矩形菜园的面积为 450 平方米,求所利用旧墙 AD 的长;
(2)求矩形菜园 ABCD 面积的最大值。
在本节课的学习中你有什么收获和感悟?
对以后的学习和生活有什么启发?
五、课堂小结,梳理交流
一个关键
“
依据常用几何图形面积公式,建立函数关系式
“
“
“
几何面积最值问题
五、课堂小结,梳理交流
一个注意
最值有时不在顶点处,则要利用函数的增减性来确定
成功不是靠梦想和希望,而是靠努力和实践。
加油吧!同学们!
谢谢大家!
再见
实际问题与二次函数之
人教版数学九年级上册
几何图形的最大面积
1.分析实际问题中变量之间的二次函数关系;(难点)
2.会运用二次函数求实际问题中的最大值或最小值;
3.能应用二次函数的性质解决图形中最大面积问题。(重点)
4.通过用二次函数解决生活中的问题,体会函数知识的应用价值,感受数学与人类生活的密切联系。
一、教学目标
求二次函数y=ax2+bx+c(a≠0)最值?
将y=ax2+bx+c(a≠0)化为y=a(x-h)2+k的形式,当x=h时,函数y取得最大(小)值,为k。
当x= 时,函数y取得最大(小)值,为 。
二、复习引入
配方法
公式法
例:用总长为60米的篱笆围成矩形场地,矩形面积S(平方米)随矩形一边长l(米)的变化而变化。当l是多少米时,场地的面积S最大?
典例精析
问题1 面积S的函数关系式是什么?
S=(30-l)l=-l2+30l
三、探究二次函数解决矩形面积问题
问题2 当l是多少米时,场地的面积S最大?
解:根据题意得
S=l(30-l)
即S=-l2+30l (0
S有最大值
也就是说,当l是15m时,场地的面积S最大。
三、探究二次函数解决矩形面积问题
5
10
15
20
25
30
100
200
l
s
O
如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园。
60-2x
x
x
(1)当墙长32m时,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
分析:设垂直于墙的边长为x m,则平行于墙的边长为________ m
矩形菜园的面积S =________________________
想一想:如何求解自变量x的取值范围?
0<60-2x≤32,即14≤x<30
(60-2x)
x(60-2x)=-2x2+60x
变式
三、探究二次函数解决矩形面积问题
三、探究二次函数解决矩形面积问题
解:设垂直于墙的边长为x m,则平行于墙的边长为(60-2x)m
∴矩形菜园的面积S=x(60-2x)=-2x2+60x
由题意得0<60-2x≤32,即14≤x<30
∵S=-2x2+60x=-2(x2-30x)=-2(x-15)2+450
∴当x=15m时,S取最大值,此时S=450m2
设未知数,用含未知数的代数式表示相关量
根据题意,求出自变量的取值范围
写出二次函数解析式,化为顶点式
结合相关量,利用面积公式求解
结合自变量的取值范围可知,该二次函数在其顶点处取得最大值。
(2)当墙长18 m时,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
解:设垂直于墙的边长为x m
由(1)知S=-2x2+60x=-2(x2-30x)=-2(x-15)2+450
问题1 与(1)有什么区别?
试一试 在(2)中,求自变量的取值范围?
21≤ x <30
是否依然在x=15时,S取得最大值?
三、探究二次函数解决矩形面积问题
问题2 当21≤ x <30时,S的值随x的增大,是如何变化的? 当x取何值时,S取得最大值?
当21≤ x <30时,S 随x的增大而减小
当 x =21时,S取得最大值
此时S=-2×(21-15)2+450=378m2
三、探究二次函数解决矩形面积问题
实际问题中求解二次函数最值问题,不一定都取图象顶点处,要根据自变量在实际情况中的取值范围进行分析。
通过前两道例题的对比,理解函数图象的顶点、端点与最值的关系以及何时取顶点处、何时取端点处才有符合实际的最值。
三、探究二次函数解决矩形面积问题
“何时取得最大面积” 解题思路
1、设自变量(一般设某条边为x,)与因变量(设“面积”为y);
2、列出y与x的函数关系式(一般为二次函数);
3、找出自变量的取值范围;
4、求利用配方法或顶点公式,求出最值。若自变量的取值范围不包括顶点横坐标,则须利用增减性求出最值。
三、探究二次函数解决矩形面积问题
如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有
二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。
四、课堂练习
拓展练习
A
B
C
D
A
B
C
D
解:
(1)∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3)∵墙的可用长度为8米
(2)当x= 时,S最大值= =36(平方米)
∴ S=x(24-4x)=-4x2+24 x (0
∴当x=4m时,S最大值=32 平方米
x
24-4x
四、课堂练习
拓展练习
(福建中考)如图,在足够大的空地上有一段长为 a m的旧墙 MN,某人利用旧墙和木栏围成一个矩形菜园 ABCD,其中 AD≤MN。已知矩形菜园的一边靠墙,另三边一共用了 100 m木栏。
四、课后作业
对接中考
(1)若 a=20,所围成的矩形菜园的面积为 450 平方米,求所利用旧墙 AD 的长;
(2)求矩形菜园 ABCD 面积的最大值。
在本节课的学习中你有什么收获和感悟?
对以后的学习和生活有什么启发?
五、课堂小结,梳理交流
一个关键
“
依据常用几何图形面积公式,建立函数关系式
“
“
“
几何面积最值问题
五、课堂小结,梳理交流
一个注意
最值有时不在顶点处,则要利用函数的增减性来确定
成功不是靠梦想和希望,而是靠努力和实践。
加油吧!同学们!
谢谢大家!
再见
同课章节目录
