24.1.2章圆周角

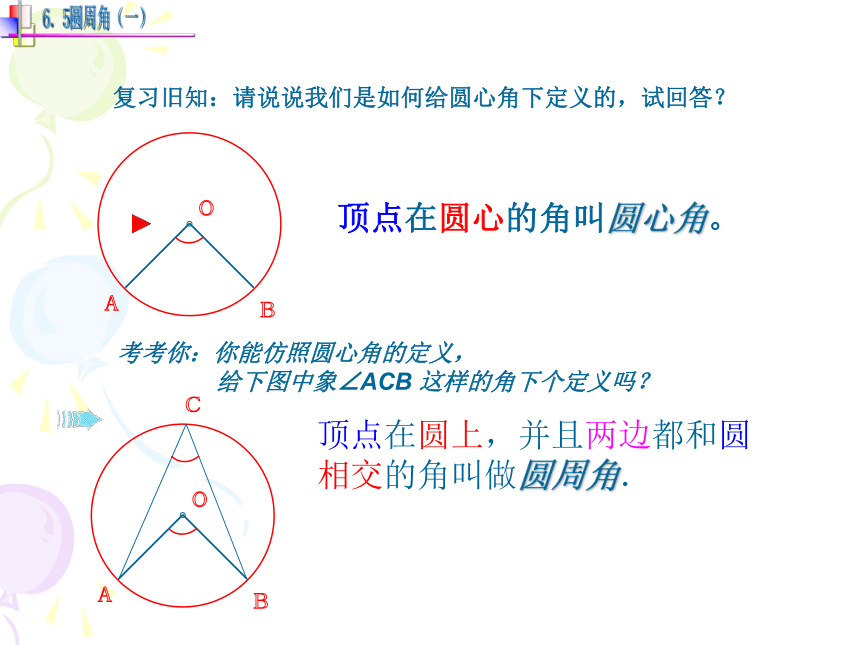
课件27张PPT。23.1圆周角 复习旧知：请说说我们是如何给圆心角下定义的，试回答？顶点在圆心的角叫圆心角。考考你：你能仿照圆心角的定义，
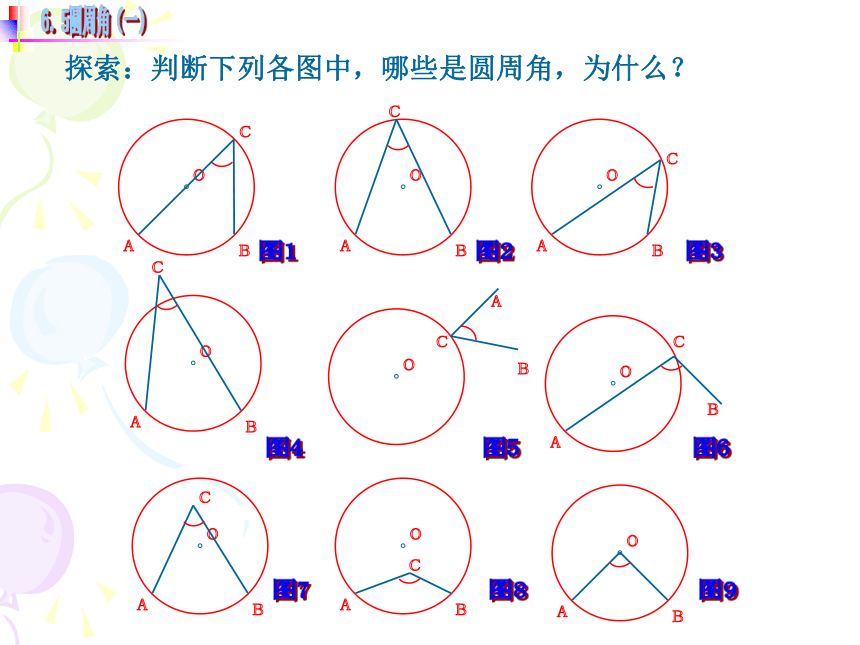
给下图中象∠ACB 这样的角下个定义吗？顶点在圆上，并且两边都和圆相交的角叫做圆周角． 探索：判断下列各图中，哪些是圆周角，为什么？ oABoABoABoABoABoABoABoABCCCCCCCC图1图2图3图4图5图6图7图8图9活动2 问题1
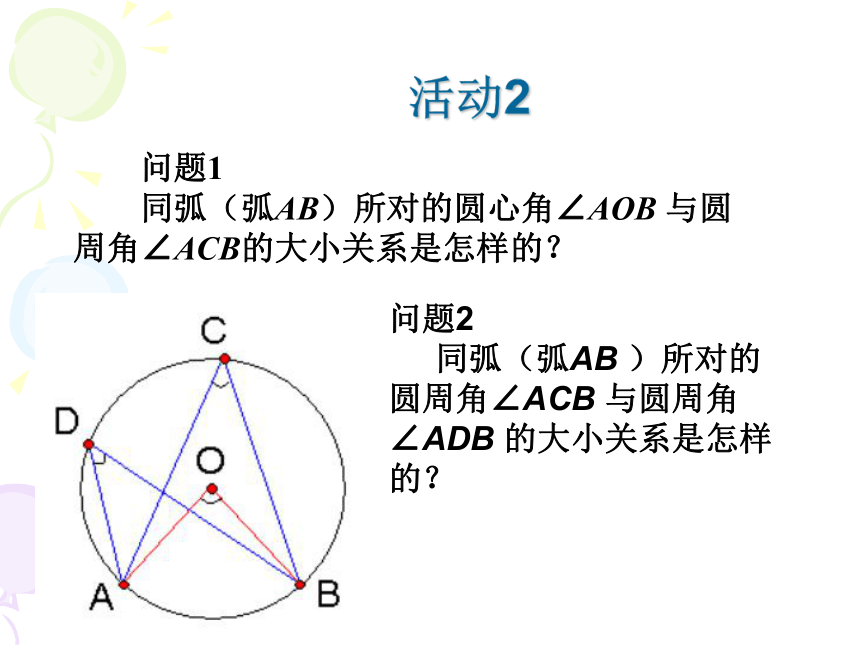
同弧（弧AB）所对的圆心角∠AOB 与圆周角∠ACB的大小关系是怎样的？ 问题2
同弧（弧AB ）所对的圆周角∠ACB 与圆周角∠ADB 的大小关系是怎样的？
画一个圆心角,然后再画同弧所对的圆周角.1.同一条弧你能画多少个圆周角?多少个圆
心角?用量角器量一量这些
圆周角你有何发现？2.再用量角器量出圆心角的度数,你有何发现 呢?发现:一条弧所对的圆周角等于它所对的圆心角的一半.探索2:发现:在同圆(或等圆)中,同弧或等弧所
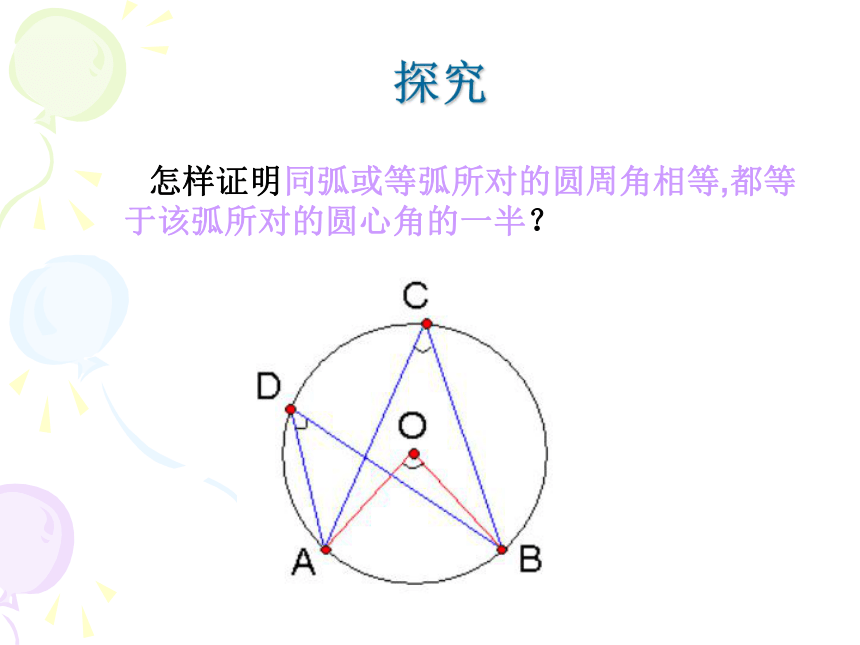
对的圆周角相等探究怎样证明同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半？ 做一做 问题1
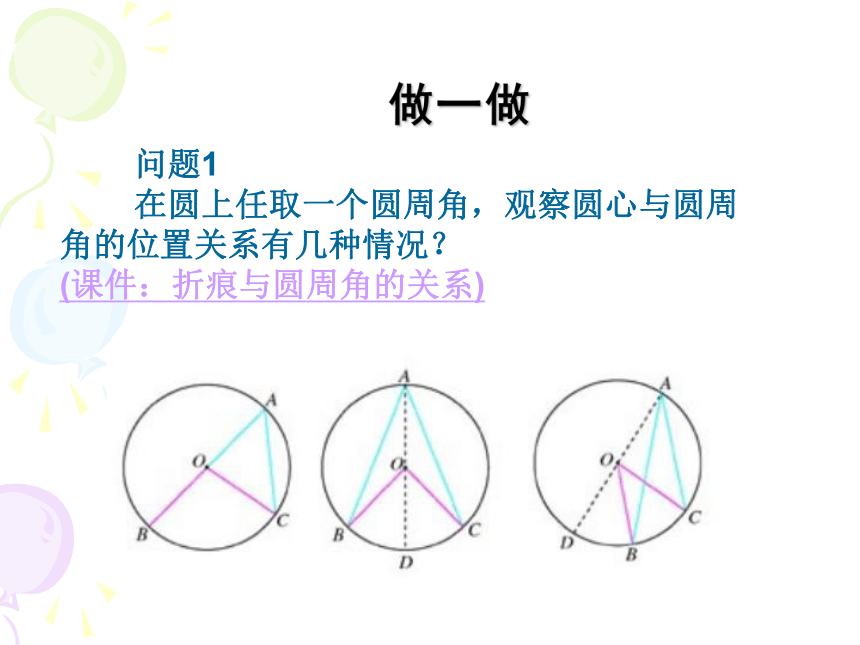
在圆上任取一个圆周角，观察圆心与圆周角的位置关系有几种情况？
(课件：折痕与圆周角的关系) 问题2
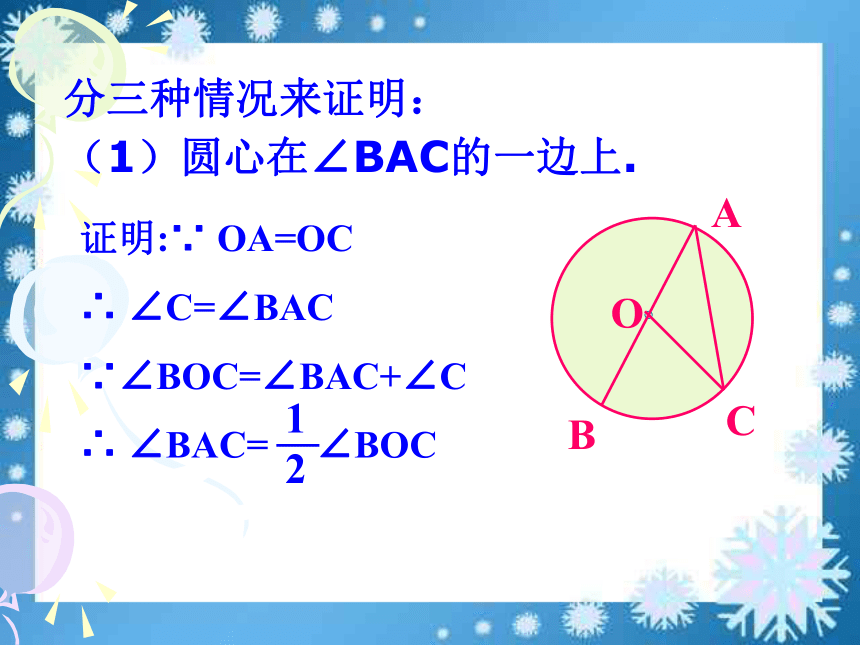
当圆心在圆周角的一边上时，如何证明？ 活动3 做一做分三种情况来证明：
（1）圆心在∠BAC的一边上.
问题3
另外两种情况如何证明呢？ 活动3 做一做练习:例题　1、在⊙O中，∠CBD=30° ,∠BDC=20°,求∠A　1、在⊙O中，∠CBD=30° ,∠BDC=20°,求∠A　　 2、如图，在⊙O中，AB为直径，CB = CF,
弦CG⊥AB，交AB于D，交BF于E
求证：BE=EC
例题⌒⌒探索如图，线段AB是⊙O的直径，点C是⊙O上任意一点（除点A、B），那么，∠ACB就是直径AB所对的圆周角，想想看，∠ACB会是怎样的角？思考
90°的圆周角所对的弦是什么? 从而得出结论：
90°的圆周角所对的弦是直径半圆（或直径）所对的圆周角是直角3、如图, ⊙O的直径 AB 为10 cm，弦 AC 为６cm,
∠ACB 的平分线交⊙O于 D, 求BC、AD、BD的长. 1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.3.在同圆(或等圆)中，同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半；相等的圆周角所对的弧相等。2.半圆或直径所对的圆周角都相等，都等于90°
90°的圆周角所对的弦是圆的直径小结:作业:1、书本94页第4、11题
2、补充习题34页第六题1.AB、AC为⊙O的两条弦，延长CA到D，使 AD=AB，如果∠ADB=35° ，
求∠BOC的度数。∠BOC =140° ∠A=21° 4、在⊙O中，一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°，则x=_ _；3. 如图，在直径为AB的半圆中，O为圆心，C、D
为半圆上的两点，∠COD=50°，则
∠CAD=______；20°50°3.虽然一条弧所对的圆周角有无数个,但它们与圆心的位置有几种情况?发现:一条弧所对的圆周角等于它所对的圆
心角的一半. 1、如图，点A、B、C、D在同一个圆上，四边形的对角线把４个
内角分成８个角，这些角中哪些是相等的角？ 练习　　2、如图：0A、OB、OC都是⊙O的半径，∠AOB=2∠BOC。求证： ∠ACB=2 ∠BAC。练习：3.如图，圆心角∠AOB=100°，
则∠ACB=___。例2 在足球比赛场上，甲、乙两名队员互相配合向对方球门MN进攻，当甲带球冲到A点时，乙已跟随冲到B点(如图2)．此时甲是自己直接射门好，还是迅速将球回传给乙，让乙射门好？分析 在真正的足球比赛中情况会很复杂，这里仅用数学方法从两点的静止状态加以考虑，如果两个点到球门的距离相差不大，要确定较好的射门位置，关键看这两个点分别对球门MN的张角大小，当张角较小时，则球容易被对方守门员拦截.怎样比较A、B两点对MN张角的大小呢？解 考虑过M、N以及A、B中的任一点作一圆，这里不妨作出⊙BMN，显然，A点在⊙BMN外，设MA交圆于C，则
　　∠MAN＜∠MCN，而∠MCN=∠MBN，
　　所以∠MAN＜∠MBN．
　　因此，甲应将球回传给乙，让乙射门.（2）圆心在∠BAC的内部.（3）圆心在∠BAC的外部.D例3:已知, ⊙O的弦AB长等于圆的半径,求该弦所对的圆心角和圆周角的度数,例题