人教版 九年级上册 第二十三章 旋转23.1图形的旋转 课件(共22张PPT)
文档属性
| 名称 | 人教版 九年级上册 第二十三章 旋转23.1图形的旋转 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 18.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-08 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
图形的旋转
年级:九年级 学科:数学(人教版)
情景引入
观察下面图片运动,其中蕴藏着哪些图形变化?
平移
轴对称
旋转
平移、轴对称研究思路是什么?
实例认识平移、轴对称
探究相关性质
利用性质进行画图
利用性质进行图案设计
利用坐标表示图形变化
图形的旋转研究思路
实例认识旋转
学习目标
1 通过类比平移、轴对称研究思路,探究旋转的
定义与性质。
2 通过灵活应用旋转的性质,解决实际问题。
3 通过欣赏旋转图案设计,感受旋转变化的魅力。
把一个平面图形绕平面内某一定点O转动一个角度,叫做图形的旋转。
以上这些现象有什么共同特点?
O
一
旋转的定义
3分钟时间,自学课本第59页下面这段文字,了解旋转中心、旋转角、对应点等相关概念。
一
自主学习
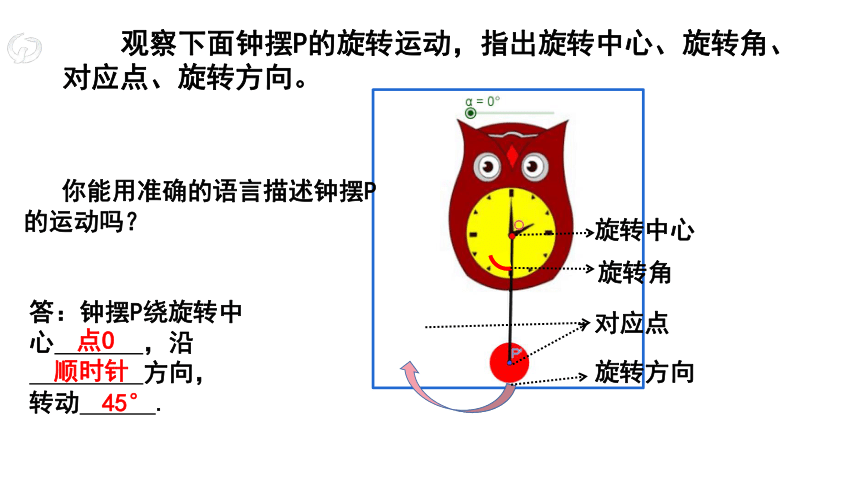
观察下面钟摆P的旋转运动,指出旋转中心、旋转角、对应点、旋转方向。
你能用准确的语言描述钟摆P的运动吗?
答:钟摆P绕旋转中心 ,沿
方向,
转动 .
点O
顺时针
45°
旋转中心
对应点
旋转角
旋转方向
画板软件制作三角形旋转
旋转三要素:
旋转中心
旋转方向
旋转角度
顺时针
逆时针
动手操作
在硬纸板上,挖出一个三角形的洞,硬纸板下面放一张白纸,先在纸上描出这个挖掉的三角形().然后用图钉钉出一个洞,作为旋转中心,按住图钉,围绕旋转中心旋转硬纸板,再描出这个挖掉的三角形(A'B'C'),移开硬纸板,将旋转中心记作O,连接对应点与旋转中心。
A
B
O
C
A'
B'
C'
旋转有哪些性质?
平移 轴对称 旋转
图形
性质
整体
变化前、后的图形全等
对应点所连线段平行(或共线)且相等
对应点所连线段被对称轴垂直平分
局部
类比探究
A
B
O
C
B'
C'
A'
性质探索
①图中△ABC与△A'B'C'的形状和大小有什么关系?
②利用直尺测量,图中线段OA与OA'、OB与OB'、OC与OC'有什么关系?
③利用量角器度量图中的旋转角,它们是否相等?
△ABC≌△A'B'C'
OA=OA';OB=OB';OC=OC'
∠AOA'=∠BOB'=∠COC'
旋转前、后的图形全等
对应点到旋转中心的距离相等
对应点与旋转中心所连线段的夹角等于旋转角
当△ABC的形状发生改变,旋转中心O发生移动时,下面结论是否依然成立呢?
性质验证
旋转前、后的图形全等
对应点到旋转中心的距离相等
对应点与旋转中心所连线段的夹角等于旋转角
旋转的性质
分析:
1.小明在制作三角形旋转过程中,不小心忘记标记旋转中心O了,你有什么办法帮他找到旋转中心?
A
B
O
C
B'
C'
A'
旋转性质得OA=OA'
点O在AA'垂直平分线上.
答:做线段AA'与CC'的垂直平分线,两线的交点O即为旋转中心.
O
当堂训练
2.如图,将△ABC 绕点A逆时针旋转得到△AB'C',点B的对应点B'恰好落在线段BC上.若∠B=60,求∠CAC'=___________.
分析:由旋转性质得
AB=AB'
∵∠B=60°
∴△ABB'为等边三角形∴∠BAB'=60°
∴∠BAB'=∠CAC'=60°
60°
当堂训练
变式:将△ABC 绕点A逆时针旋转得到△AB'C',点B的对应点B'恰好落在线段BC上.若∠CAC'=58°,求∠B= .
61°
分析:由旋转性质得
∠BAB'=∠CAC'=58°
AB=AB'
∴∠B=∠AB'B=61°
当堂训练
当堂训练
3.如图1,E是正方形ABCD中CD边上任意一点,图1中左面的△ADE经过怎样的旋转,可以得到右面图形?
答:把图1 的左面的△ADE以点A为旋转中心,沿逆时针方向分别旋转90°、180°、270°,得到图1右面图形.
图1
你还有其他做法吗?
旋转欣赏
将基本图形1,绕点O旋转不同的角度会出现怎样的效果呢?
图1
课堂小结
平移
轴对称
旋转
类比
旋转
旋转中心
旋转角
对应点
定义
性质
旋转前、后的图形全等
对应点到旋转中心的距离相等
对应点与旋转中心所连线段的夹角等于旋转角
作业布置
1.(基础练习)完成课本P61第1,2,3题.
2.(变式练习)如图,将△ABC 绕点A逆时针旋转58°得到△AB'C',点B的对应点B'恰好落在线段BC上,求∠CB'C'=___________.
3.(拓展练习)完成课本P63第10题.
感谢聆听
图形的旋转
年级:九年级 学科:数学(人教版)
情景引入
观察下面图片运动,其中蕴藏着哪些图形变化?
平移
轴对称
旋转
平移、轴对称研究思路是什么?
实例认识平移、轴对称
探究相关性质
利用性质进行画图
利用性质进行图案设计
利用坐标表示图形变化
图形的旋转研究思路
实例认识旋转
学习目标
1 通过类比平移、轴对称研究思路,探究旋转的
定义与性质。
2 通过灵活应用旋转的性质,解决实际问题。
3 通过欣赏旋转图案设计,感受旋转变化的魅力。
把一个平面图形绕平面内某一定点O转动一个角度,叫做图形的旋转。
以上这些现象有什么共同特点?
O
一
旋转的定义
3分钟时间,自学课本第59页下面这段文字,了解旋转中心、旋转角、对应点等相关概念。
一
自主学习
观察下面钟摆P的旋转运动,指出旋转中心、旋转角、对应点、旋转方向。
你能用准确的语言描述钟摆P的运动吗?
答:钟摆P绕旋转中心 ,沿
方向,
转动 .
点O
顺时针
45°
旋转中心
对应点
旋转角
旋转方向
画板软件制作三角形旋转
旋转三要素:
旋转中心
旋转方向
旋转角度
顺时针
逆时针
动手操作
在硬纸板上,挖出一个三角形的洞,硬纸板下面放一张白纸,先在纸上描出这个挖掉的三角形().然后用图钉钉出一个洞,作为旋转中心,按住图钉,围绕旋转中心旋转硬纸板,再描出这个挖掉的三角形(A'B'C'),移开硬纸板,将旋转中心记作O,连接对应点与旋转中心。
A
B
O
C
A'
B'
C'
旋转有哪些性质?
平移 轴对称 旋转
图形
性质
整体
变化前、后的图形全等
对应点所连线段平行(或共线)且相等
对应点所连线段被对称轴垂直平分
局部
类比探究
A
B
O
C
B'
C'
A'
性质探索
①图中△ABC与△A'B'C'的形状和大小有什么关系?
②利用直尺测量,图中线段OA与OA'、OB与OB'、OC与OC'有什么关系?
③利用量角器度量图中的旋转角,它们是否相等?
△ABC≌△A'B'C'
OA=OA';OB=OB';OC=OC'
∠AOA'=∠BOB'=∠COC'
旋转前、后的图形全等
对应点到旋转中心的距离相等
对应点与旋转中心所连线段的夹角等于旋转角
当△ABC的形状发生改变,旋转中心O发生移动时,下面结论是否依然成立呢?
性质验证
旋转前、后的图形全等
对应点到旋转中心的距离相等
对应点与旋转中心所连线段的夹角等于旋转角
旋转的性质
分析:
1.小明在制作三角形旋转过程中,不小心忘记标记旋转中心O了,你有什么办法帮他找到旋转中心?
A
B
O
C
B'
C'
A'
旋转性质得OA=OA'
点O在AA'垂直平分线上.
答:做线段AA'与CC'的垂直平分线,两线的交点O即为旋转中心.
O
当堂训练
2.如图,将△ABC 绕点A逆时针旋转得到△AB'C',点B的对应点B'恰好落在线段BC上.若∠B=60,求∠CAC'=___________.
分析:由旋转性质得
AB=AB'
∵∠B=60°
∴△ABB'为等边三角形∴∠BAB'=60°
∴∠BAB'=∠CAC'=60°
60°
当堂训练
变式:将△ABC 绕点A逆时针旋转得到△AB'C',点B的对应点B'恰好落在线段BC上.若∠CAC'=58°,求∠B= .
61°
分析:由旋转性质得
∠BAB'=∠CAC'=58°
AB=AB'
∴∠B=∠AB'B=61°
当堂训练
当堂训练
3.如图1,E是正方形ABCD中CD边上任意一点,图1中左面的△ADE经过怎样的旋转,可以得到右面图形?
答:把图1 的左面的△ADE以点A为旋转中心,沿逆时针方向分别旋转90°、180°、270°,得到图1右面图形.
图1
你还有其他做法吗?
旋转欣赏
将基本图形1,绕点O旋转不同的角度会出现怎样的效果呢?
图1
课堂小结
平移
轴对称
旋转
类比
旋转
旋转中心
旋转角
对应点
定义
性质
旋转前、后的图形全等
对应点到旋转中心的距离相等
对应点与旋转中心所连线段的夹角等于旋转角
作业布置
1.(基础练习)完成课本P61第1,2,3题.
2.(变式练习)如图,将△ABC 绕点A逆时针旋转58°得到△AB'C',点B的对应点B'恰好落在线段BC上,求∠CB'C'=___________.
3.(拓展练习)完成课本P63第10题.
感谢聆听
同课章节目录
